Abstract
Although many megacities in developing countries experience floods annually that affect a large number of people, relatively few empirical studies have evaluated the associated costs. This paper estimates such costs by conducting a hedonic price analysis—providing evidence regarding the impacts of floods on the housing market. A robust regression technique on a simple linear transformation model, and a maximum likelihood estimation technique on the spatial lag version of the simple linear transformation model, are utilised to estimate the correlation between the level of the 2007 floods and monthly housing rental prices in Jakarta, Indonesia. This paper sheds light on the fact that in developing countries’ megacities, the total cost of floods among households is significantly lower compared to the total amount of funding needed to permanently eliminate floods in these megacities. Hence, a constant exposure of the urban areas in developing countries to flood damage will most likely keep happening.

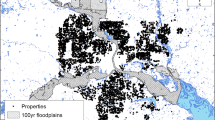
Source: United Nations Department of Safety and Security (UNDSS), 2007
Similar content being viewed by others
Notes
Value measured as a monthly rate—represented as dependent variable monthly rent—is based on potential and actual rental prices. This considers the fact that 70% of observations represent owner-occupied homes with no set rental price, therefore it is considered as a potential rental price only [asked as “Rent would pay per month” (IFLS 2007)]. The other 30% are renter-occupied homes with an actual rental price.
Another option is to use the average treatment effect using the spatial lag model. Assuming a dummy variable of flooding, the house equals one whether it was flooded in 2007 at certain water level (e.g., 30 cm, 50 cm or 60 cm) and above, and zero otherwise. The findings are presented in “Appendix D”. Since they are sensitive towards the definition of flooded house or not, this paper prefers to utilise a continuous variable of flood level.
Following Follain and Malpezzi, we test the functional form chosen to determine whether it suits our data set better than that of using a linear model. In this regard, the Box-Cox test was utilised to compare the goodness-of-fit of the two functional forms. Given the results, in our case, they are significantly different in terms of goodness-of-fit; the log-linear function has a lower residual sum of squares compared to that of the linear functional form. Therefore, we use the log-transformed model to look at the coefficients of the empirical model.
Similarly, a spatial error model can be considered, which supposes that spatial dependence arises due to measurement errors or some omitted variables that are correlated and vary spatially. The Lagrange multiplier (statistic = 23.710; p value = 0.000) and the robust Lagrange multiplier (statistic = 12.039; p value = 0.001) tests show spatial error dependence. The spatial error model findings are discussed in more detail in “Appendix E” where it can be seen that the flood coefficient is relatively similar to that of the spatial lag model. This paper prefers to utilise the results for the spatial lag model for its analysis and conclusion, since the spatial lag model is simpler and the spatial correlation can be explicitly seen.
Additionally, an OLS regression is applied to analyse whether or not the effects of flooding on rental prices for Jakarta residents are similar for both owner occupied and rentals. The results of this analysis are shown in “Appendix F” and indicate that rentals are more likely to be vulnerable to impacts of flooding.
Housing attributes are mainly represented by dummies, so it is possible the OLS model has a certain degree of multicollinearity. This could explain the low significance levels and opposite signs obtained from a linear regression. Variance inflation factors (VIFs) are used to test for multicollinearity among the independent variables. According to Gujarati (1995), multicollinearity may be a problem if the VIF is greater than 10. In this study, the mean of the VIF values for all of the variables was 1.90 for the OLS regression. This means there is no multicollinearity or no correlation between the independent variables.
References
Anselin L (1988) Spatial econometrics: methods and models. Kluwer Academic Publishers, Boston
Atreya A, Ferreira S, Kriesel W (2013) Forgetting the flood?: an analysis of the flood risk discount over time. Land Econ 89(4):577–596
Baker J (2011) Climate change, disaster risk, and the urban poor: cities building resilience for a changing world. World Bank, Washington
Bappenas (2007) Laporan Perkiraan Kerusakan dan Kerugian Pasca Bencana Banjir Awal Februari 2007 di Wilayah JABODETABEK (Jakarta, Bogor, Depok, Tangerang, dan Bekasi). Technical report, Kementerian Negara Perencanaan Pembangunan Nasional/BAPPENAS, Jakarta
Basu S, Thibodeau TG (1998) Analysis of spatial autocorrelation in house prices. J Real Estate Finance Econ 17:61–85
Bin O, Landry C (2013) Changes in implicit flood risk premiums: empirical evidence from the housing market. J Environ Econ Manag 65(3):361–376
Bin O, Polasky S (2004) Effects of flood hazards on property values: evidence before and after hurricane Floyd. Land Econ 80(4):490–500
Bin O, Crawford T, Kruse J, Landry C (2008a) Viewscapes and flood hazard: coastal housing market response to amenities and risk. Land Econ 84(3):434–448
Bin O, Kruse J, Landry C (2008b) Flood hazards, insurance rates and amenities: evidence from the coastal housing market. J Risk Insur 75(1):63–82
Brasington DM, Hite D (2005) Demand for environmental quality: a spatial hedonic analysis. Reg Sci Urban Econ 35(1):57–82
Budiyono Y, Aerts JCJH, Brinkman J, Marfai MA, Ward PJ (2015) Flood risk assessment for delta mega–cities: a case study of Jakarta. Nat Hazards 75:389–413
Budiyono Y, Aerts JCJH, Tollenaar D, Ward PJ (2016) River flood risk in Jakarta under scenarios of future change. Nat Hazards Earth Syst Sci 16:757–774
Carbone J, Hallstrom D, Smith V (2006) Can natural experiments measure behavioural responses to environmental risks? Environ Resour Econ 33(3):273–297
CEIC Data (2017) see CEIC Data Company Limited
Cho S, Clark C, Park W, Kim S (2009) Spatial and temporal variation in the housing market values of lot size and open space. Land Econ 85(1):51–73
Cohen B (2004) Urban growth in developing countries: a review of current trends and a caution regarding existing forecasts. World Dev 32(1):23–51
Daniel V, Florax R, Rietveld P (2007) Long term divergence between ex-ante and ex-post hedonic prices of the Meuse River flooding in The Netherlands. Discussion Paper, European Regional Science Association. http://www.tbm.tudelft.nl/fileadmin/Faculteit/CiTG/Over_de_faculteit/Afdelingen/Afdeling_Waterbouwkunde/sectie_waterbouwkunde/people/personal/gelder/publications/citations/doc/citatie_806.pdf. Accessed 14 Apr 2016
Follain J, Malpezzi S (1980) Estimates of housing inflation for thirty-nine SMSAs: An alternative to the consumer price index. Annal Reg Sci 14(3):41–56
Garschagen M, Harb M, Surtiari G (2018) Is Jakarta’s new flood risk reduction strategy transformational? Sustainability 10(2934):1–18
Gujarati DN (1995) Basic econometrics. McGraw-Hill International Editions, New York
Halvorsen R, Pollakowski HO (1981) Choice of functional form for hedonic price equations. J Urban Econ 10(1):37–49
Jha K, Bloch R, Lamond J (2012) Cities and flooding: a guide to integrated urban flood risk management for the 21st century. World Bank, Washington
Kousky C (2010) Learning from extreme events: risk perceptions after the flood. Land Econ 86(3):395–422
Kousky C, Walls M (2014) Floodplain conservation as a flood mitigation strategy: examining costs and benefits. Ecol Econ 104:119–128
Lancaster KJ (1966) A new approach to consumer theory. J Polit Econ 74(2):132–157
Leggett C, Bockstael NE (2000) Evidence of the effects of water quality on residential land prices. J Environ Econ Manag 39(2):121–144
Malpezzi S (2002) Hedonic pricing models: a selective and applied review. The Center for Urban Land Economics Research, University of Wisconsin, Wisconsin
Perticone A, Coveney C (2017) The effects from public transportation on property values: a closer look at Scituate, Hanover, and Norwell, Massachusetts. J Environ Resour Econ Colby 4(1):1–16 (article 4)
Pope J (2008) Do seller disclosures affect property values? buyer information and the hedonic model. Land Econ 84(4):551–572
Rabassa MJ, Zoloa JI (2016) Flooding risks and housing markets: a spatial hedonic analysis for La Plata City. Environment and Development Economics. http://www.saerargentina.com.ar/trabajos/8%20-%20Zoloa%20–%20Flooding%20risk%20La%20Plata.pdf. Accessed 9 June 2016
Rosen S (1974) Hedonic prices and implicit markets: product differentiation in pure competition. J Polit Econ 82(1):34–55
Samarasinghe O, Sharp B (2010) Flood prone risk and amenity values: a spatial hedonic analysis: a spatial hedonic analysis. Aust J Agric Resour Econ 54(4):457–475
Skantz T, Strickland T (1987) House prices and a flood event—an empirical investigation of market efficiency. J Real Estate Res 2(2):75–83
Stern N (2007) The economics of climate change: the stern review. Cambridge University Press, Cambridge
Tambun L, Lumanauw N, Marhaenjati B (2015) ‘Jakarta’s flood problem totally solvable, for $9,2b. Jakarta Globe
United Nations Department of Economic and Social Affairs, Population Division (2014) World urbanization prospects: the 2014 revision. https://esa.un.org/unpd/wup/Publications/Files/WUP2014-Highlights.pdf. Accessed 10 June 2016
United Nations Office for Disaster Risk Reduction (2002) Guidelines for reducing flood losses. http://www.unisdr.org/files/558_7639.pdf. Accessed 14 Mar 2016
United Nations & World Bank (2010) Natural hazards, unnatural disasters: the economics of effective prevention. World Bank, Washington, D.C.
Wahab R, Tiong R (2017) Multi-variate residential flood loss estimation model for Jakarta: an approach based on a combination of statistical techniques. Nat Hazards 86:779–804
Wijayanti P, Zhu Tiong R, Hellegers P, Budiyono Y, Van Ierland EC (2017) Estimation of river flood damages in Jakarta. Nat Hazards 86:1059–1079
Wooldridge J (2003) Introductory econometrics: a modern approach, 2d edn. Thompson and Southwestern, Cincinnati
World Bank (2011) Climate change, disaster risk and the urban poor: cities building resilience for a changing world. World Bank, Washington, D.C.
World Bank (2016) Feature story: keeping Indonesia’s capital safer from floods. World Bank, Jakarta. http://www.worldbank.org/en/news/feature/2016/01/08/keeping-indonesias-capital-safer-from-floods. Accessed 8 Jan 2016
World Resources Institute (2015) World’s 15 countries with the most people exposed to river floods. http://www.wri.org/blog/2015/03/world%E2%8%99s-15-countries-most-people-exposed-river-floods. Accessed 14 Mar 2016
Yusuf AA, Koundouri P (2005) Willingness to pay for water and location bias in hedonic price analysis: evidence from the Indonesian housing market. Environ Dev Econ 10(6):821–836
Yusuf A et al (2009) Does clean air matter in developing countries’ megacities? a hedonic price analysis of the Jakarta housing market, Indonesia. Ecol Econ 68(5):1398–1407
Acknowledgements
The authors would like to thank M. Agung Widodo for managing the IFLS data set for this paper. Some financial supports were received from the Australia Indonesia Centre (AIC). All mistakes are the authors’ responsibility.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Hedonic property value method
The hedonic price method provides an intuitive analytical tool for studying the effects of property attributes and spatially integrated amenities on housing prices. Lancaster (1966) pioneered the development of its theoretical foundations, derived from the theory of consumer demand. The central assumption is that consumer utilities are not based on the goods per se, but instead on the individual “characteristics” of goods—their composite attributes. Although Lancaster (1966) was the first to discuss hedonic utility, there was nothing about pricing models and the properties of market equilibrium. To fill this gap, Rosen (1974) studied the demand–supply interaction in which they bid (consumers) and offer (suppliers) the combination of attributes and prices of the goods that keep the market in equilibrium.
Additionally, Rosen’s (1974) studies form the basis for using the hedonic property price model to estimate the value of environmental amenities. The argument is that the attributes of residential properties—recognised as heterogeneous goods, such as structural, neighbourhood and environmental characteristics—are reflected in the price differentials that affect lessee preferences in a market clearing equilibrium condition (Rosen 1974). The advantage of using this method over other preference estimation techniques is that it makes use of actual market transactions to recover value estimates for non-market attributes (Bin et al. 2008a). These related to aesthetic sights and their closeness to recreational sites such as parks, and beaches, as well as the quality of the environment in terms of air, water and noise pollution.
According to this method, the hedonic price function is typically represented as:
where \(P_{i}\) is the price of property \(i\) which is a function of structural characteristics (e.g., house size, number of rooms, quality of walls), \(s\); neighbourhood characteristics (for example, ethnic composition, crime rate, flow of traffic), \(n\); location characteristics (e.g., proximity to economic centres, distance to highways, accessibility to public transport), \(l\); and environmental characteristics (such as air pollution and flooding), \(e\). Therefore, characteristics that generate benefits for households, such as a larger number of rooms or home size, increase the property’s price, while characteristics that imply costs for households, such as a neighbourhood with a high crime rate, reduce the property’s price.
Given that the basis of the method is to find what portion of the price is determined by the hedonic variable, we obtain the environmental attribute (which is flooding) by calculating the partial derivative of the price with respect to the variable \(e\), ∂\(P_{i}\)/∂\(e\). It gives us the marginal implicit value for an additional unit of the environmental asset, and thus enables an estimate of its monetary value.
Appendix B: Mean comparison between IFLS and SUSENAS datasets
To support the representation of Jakarta’s population, we provide the means of certain variables from Indonesia–National Socio-Economic Survey (SUSENAS) 2007 that was accessed for this paper. The following table shows the means compared with those of IFLS 2007 (Table 4).
Appendix C: Distribution of independent variables
The below table represents the distribution of continuous variables when they are in levels. Those on the left, demonstrate the skewed towards zero on the axis, while those on the right demonstrate a spread across the axis (i.e., closer to normal distribution) (Fig. 2).
Appendix D: Spatial average treatment effect model
Unlike previous studies, this study uses a continuous measure of flood water (in centimetres) in the empirical analysis. To find whether or not a house within the flooded area lowers the rental price at any certain water level, we construct a conventional binary measure of flooding at the neighbourhood level based on three different threshold water levels, e.g., 30, 50 and 60. A house is considered flooded when the water level in the area during the flood event in 2007 was 30 cm (or 50 cm or 60 cm) and above; otherwise, the house is considered not flooded. We then estimate the impact of flooding on location rental prices using the spatial lag model:
From Table 5, it can be seen that results are sensitive towards the definition of being flooded or not, i.e., flood water thresholds define whether the house is flooded or not. However, it should be considered that any marginal difference between the chosen flood levels (e.g., from 30 to 50 cm and 50 to 60 cm) could be irrelevant and trivial for a household, as they are still experiencing flooding with its associated damage to the home. Therefore, we prefer to use a continuous flood-level variable as our main variable of interest.
Appendix E: Estimation results using spatial error model
The spatial error model takes the following form:
where \(\mu\) is the independent and identically distributed (i.i.d.) error term and \(\lambda\) is the spatial error parameter. The understanding of the spatial error model is close to the moving average model, whereby each observation error in the time series can also be affected by other observation errors. Ignoring the spatial error term, the OLS coefficients will be inefficient as it violates the assumption of independence among disturbance terms (Anselin 1988) (Table 6).
Appendix F: Owner-occupied and rental property comparison
When running separate regression for the dummy variable homeowner (1,0), we find that the study variable (LOGflood) is statistically significant at 5% for rental properties. This means that those renting are likely to be more vulnerable to flood impacts than those owning or buying. Owning a home can be considered as an indicator of income and economic resources that may support flood victims to cope with the effects of flooding (Table 7).
About this article
Cite this article
Cobián Álvarez, J., Resosudarmo, B.P. The cost of floods in developing countries’ megacities: a hedonic price analysis of the Jakarta housing market, Indonesia. Environ Econ Policy Stud 21, 555–577 (2019). https://doi.org/10.1007/s10018-019-00242-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10018-019-00242-w