Abstract
We examine the effects of trade liberalization in environmental goods in a model with one domestic downstream polluting firm and two upstream firms (one domestic, one foreign). The upstream firms offer their technologies to the downstream firm at a flat fee. The domestic government sets the emission tax rate after the outcome of R&D is known. The effect of liberalization on the domestic upstream firm’s R&D incentive is ambiguous. Liberalization usually results in cleaner production, which allows the country to reach higher welfare. However, this increase in welfare is typically achieved at the expense of the environment (a backfire effect).
Similar content being viewed by others
Notes
Antweiler et al. (2001) find that trade liberalization has generally reduced SO\({_{2}}\) concentrations. Cole and Elliott (2003) suggest it will reduce BOD, but increase CO\(_{2}\) and NO\(_{x}\) emissions. Managi et al. (2009) conclude that trade has benefited the environment in OECD countries, but increased SO\(_{2}\) and CO\(_{2}\) emissions elsewhere. Lovely and Popp (2011) empirically examine two effects of trade openness: While it improves access to the latest clean technologies, it also reduces industry’s ability to pass on regulatory costs to consumers.
See Sinclair-Desgagné (2008) for a description of the global eco-industry.
OECD (2005) predicts that the EGS market will grow by less than 1 % annually in developed countries and by 8.6 % in the developing countries, while Sinclair-Desgagné (2008) predicts growth figures of 3–5 and 10–15 % respectively. In 2003, nearly 80 % of the global exports of EGS originated in developed countries (Hamwey 2005).
In a different context, with heterogeneous firms and an exogenously fixed emission tax rate, Bréchet and Ly (2013) also show that the adoption of cleaner technology can increase pollution.
All papers discussed here assume welfare-maximizing governments. See Canton (2008) for a political-economy model with the eco-industry in an international setting.
If there were multiple downstream firms, we would have to consider the upstream firms’ incentives to increase revenue by licensing to a limited number of firms at a higher fee.
If \(K_{i}=0,\) technology i is a blueprint that requires no equipment.
Price competition can be seen as the process that endogenizes bargaining power, resulting in complete (no) bargaining power for firm 1 (2) vis-a-vis the downstream firm.
In fact, in scenario nn, the upstream firms compete the fee down to \(K_{n}\) and the downstream firm as well as the government are indifferent between the two suppliers. For expositional simplicity, we let the domestic firm supply the technology.
Trade liberalization which opens up the domestic market to the foreign upstream firm always increases the foreign firm’s R&D incentive, because its net revenue from licensing to the domestic downstream firm is higher (or at least equally high) with the new technology.
Further details are available from the corresponding author upon request.
References
Antweiler W, Copeland BR, Taylor MS (2001) Is free trade good for the environment? Am Econ Rev 91:877–908
Biglaiser G, Horowitz JK (1995) Pollution regulation and incentives for pollution-control research. J Econ Manag Strategy 3:663–684
Binswanger M (2001) Technological progress and sustainable development: what about the rebound effect? Ecol Econ 36:119–132
Bréchet T, Ly S (2013) The many traps of green technology promotion. Environ Econ Policy Stud 15:73–91
Canton J (2008) Redealing the cards: how an eco-industry modifies the political economy of environmental taxes. Resour Energy Econ 30:295–315
Cole MA, Elliott RJR (2003) Determining the trade-environment composition effect: the role of capital, labor and environmental regulations. J Environ Econ Manag 46:363–383
David M, Nimubona AD, Sinclair-Desgagné B (2011) Emission taxes and the market for abatement goods and services. Resour Energy Econ 33:179–191
De Melo J, Vijil M (2014) Barriers to trade in environmental goods and environmental services: how important are they? How much progress at reducing them? Nota di lavoro 36.2014, FEEM
Feess E, Muehlheusser G (2002) Strategic environmental policy, clean technologies and the learning curve. Environ Resour Econ 23:149–166
Fisher-Vanden K, Ho MS (2010) Technology, development, and the environment. J Environ Econ Manag 59:94–108
Fischer C, Parry IWH, Pizer WA (2003) Instrument choice for environmental protection when technological innovation is endogenous. J Environ Econ Manag 45:523–545
Greaker M (2006) Spillovers in the development of new pollution abatement technology: a new look at the Porter hypothesis. J Environ Econ Manag 56:411–420
Greaker M, Rosendahl KE (2008) Environmental policy with upstream pollution abatement technology firms. J Environ Econ Manag 56:246–259
Hamwey R (2005) Environmental goods: where do the dynamic trade opportunities for developing countries lie? Working paper prepared to support discussions at the Hong Kong Trade and Development Symposium and the sixth WTO ministerial Conference in Hong Kong in December 2005
Hanley N, McGregor P, Swales JK, Turner K (2009) Do increases in energy efficiency improve environmental quality and sustainability? Ecol Econ 68:692–709
Jaffe AB, Newell RG, Stavins RN (2003) Technological change and the environment. In: Maler KG, Vincent JR (eds). Handbook of environmental economics, vol I, pp 461–516
Khazzoom DJ (1980) Economic implications of mandated efficiency standards for household appliances. Energy J 1:21–40
Laffont JJ, Tirole J (1996) Pollution permits and environmental innovation. J Public Econ 62:127–140
Lovely M, Popp D (2011) Trade, technology, and the environment: does access to technology promote environmental regulation? J Environ Econ Manag 61:16–35
Managi S, Hibiki A, Tsurumi T (2009) Does trade openness improve environmental quality? J Environ Econ Manag 58:346–363
Milliman SR, Prince R (1989) Firms incentives to promote technological change in pollution control. J Environ Econ Manag 17:247–265
Nimubona AD (2012) Pollution policy and trade liberalization of environmental goods. Environ Resou Econ 53:323–346
OECD (2003) Environmental goods and services: the benefits of further global trade liberalisation. OECD, Paris
OECD (2005) Trade that benefits the environment and development: opening markets for environmental goods and services. OECD, Paris
Parry W (1995) Optimal pollution taxes and endogenous technological progress. Resour Energy Econ 17:69–85
Parry W (1998) Pollution regulation and the efficiency gains from technological innovation. J Regul Econ 14:229–254
Perino G (2010) Technology diffusion with market power in the upstream industry. Environ Resour Econ 46:403–428
Requate T (2005a) Dynamic incentives by environmental policy instruments—a survey. Ecol Econ 54:175–195
Requate T (2005b) Timing and commitment of environmental policy, adoption of new technology, and repercussions on R&D. Environ Resour Econ 31:175–199
Saunders HD (2000) A view from the macro side: rebound, backfire, and Khazzoom-Brookes. Energy Policy 28:439–449
Sinclair-Desgagné B (2008) The environmental goods and services industry. Int Rev Environ Resour Econ 2:69–99
UNEP, ITC and ICTSD (2012) “Trade and environment briefings: Trade in environmental goods”, ICTSD Programme on Global Economic Policy and Institutions; Policy Brief No. 6; International Centre for Trade and Sustainable Development, Geneva, Switzerland. http://www.ictsd.org/sites/default/files/research/2012/06/trade-in-environmental-goods
USTR (2014) “Remarks by United States Trade Representative Michael Froman announcing new talks towards increased trade in environmental goods”, United States Trade Representative, 24 January 2014. https://ustr.gov/about-us/policy-offices/press-office/press-releases/2014/January/USTR-Froman-remarks-on-new-talks-towards-increased-trade-environmental-goods
World Trade Organization (2001) Ministerial declaration, ministerial conference, fourth session, Doha, 9–14 November 2001
Zhang ZX (2013) Trade in environmental goods, with focus on climate-friendly goods and technologies. In: van Calster G, Prévost D (eds) Research handbook on environment, health and the WTO. Edward Elgar, Northampton, pp 673–699
Acknowledgements
We thank Rod Falvey, Arijit Mukherjee, Joanna Poyago-Theotoky, the anonymous referee and seminar attendants at ZEW Mannheim and the Universities of Strathclyde (Glasgow) and Tor Vergata (Rome) for valuable comments. Any remaining errors are our own. The views expressed in this paper do not reflect the views of NOMS, the Ministry of Justice or Her Majesty’s Government.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Conditions for \(q_{2}^{s}>0\)
Autarky. \(q_{d}^{id}\) in (19) is decreasing in \(\lambda\) and has an interior minimum in \(e_{i}\in \left[ 1/\sqrt{\lambda };1\right]\) given \(\lambda\). To make sure that \(q_{d}^{id}>0\) for all \(e_{i}\in \left[ 1/\sqrt{\lambda };1\right] ,\) we calculate the \(\lambda\) where the minimum equals zero. Setting \(q_{d}^{id}=0\) and \(dq_{d}^{id}/de_{i}=0\) in (19) yields, respectively:
The only positive solution for \(\lambda\) and \(e_{i}\) is \(\lambda =\frac{5}{2 }\sqrt{5}+\frac{11}{2}.\) Therefore, \(q_{d}^{id}>0\) for all \(e_{i}\in \left[ 1/ \sqrt{\lambda };1\right]\) if and only if:
Free trade. Comparing (19) and (24), we see that \(q_{f}^{nf}>q_{d}^{nd}\) by (18). Thus, condition (44) that ensures \(q_{d}^{nd}>0\) is also sufficient for \(q_{f}^{nf}>0.\)
Output \(q_{h}^{jh},\ j=f,n,\) in (29) is positive for all values of \(e_{j}\) for which the second-order condition holds (which implies that the denominator on the RHS of (29) is positive) if and only if:
where \(\hat{e}_{j}\) as a function of \(e_{h}\) and \(\lambda\) is implicitly defined by:
The point where the LHS of (45) switches from \(+\infty\) to \(-\infty\) is where
and (46) holds. Solving (46) and (47) simultaneously for \(\lambda\) and \(e_{j},\) we find that the only positive real solution features \(\lambda =\frac{1}{2e_{h}^{2}}\left( 3\sqrt{5} +5\right) .\) Then, \(q_{h}^{jh}>0\) for all \(e_{j}\) if and only if:
Appendix 2: The licence fee
In Sect. 4, we introduced the restriction that the licence fee should be decreasing in \(e_{1}.\) In this appendix, we discuss the conditions under which this is the case.Footnote 15
1.1 Autarky
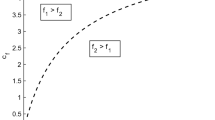
Figure 1 shows the licence fee \(F_{h}^{id}\) (given by 20) as a function of \(e_{i}\) for different values of \(\lambda\) with \(\tilde{\alpha }=1\). The condition \(dF_{h}^{id}/de_{i}<0\) is binding for \(i=n,\) because it is clear from Fig.1 that when \(dF_{h}^{nd}/de_{n}<0,\) then \(dF_{h}^{hd}/de_{h}<0\) as well, since \(e_{h}>e_{n}\). Thus, \(e_{n}\) should exceed \(\bar{e}_{n},\) where \(\bar{e}_{n}\) is defined implicitly by:
1.2 Free trade
Domestic firm has found the new technology. Comparing \(dF_{h}^{nf}/de_{n}\) in (25) to \(dF_{h}^{nd}/de_{n}\) in (20) with \(i=n,\) we see that qualitatively the only difference lies in the less efficient technology 2 which has \(e_{f}<1\) in scenario nf and \(e=1\) in nd. At \(\bar{e}_{n}\) as defined by (49) we must have \(dt^{nd}/de_{n}>0\) by (13). Then, since emissions with the less efficient technology \(E_{2}\) are lower in scenario nf than in nd, \(dF_{h}^{nf}(\bar{e}_{n})/de_{n}<0\) and \(dF_{h}^{nf}/de_{n}=0\) occurs at an \(e_{n}<\bar{e}_{n}\).
Domestic firm has not found the new technology. It can be shown that \(F_{f}^{jh}\) in (30)\(,j=n,f,\) is first increasing and then decreasing in \(e_{j}.\) Then, the condition \(dF_{f}^{jh}/de_{j}<0\) is binding for \(j=n,\) since when \(dF_{f}^{nh}/de_{n}<0,\) then \(dF_{h}^{fh}/de_{f}<0\) as well, since \(e_{f}>e_{n}\). Thus, \(e_{n}\) should exceed \(\tilde{e}_{n},\) where \(\tilde{e}_{n}\) is defined implicitly by:
It can be shown that \(\tilde{e}_{n}(e_{h})\) is an increasing function of \(e_{h}\).
1.3 Conclusion
We have found two minimum values of \(e_{n}\): \(\bar{e}_{n}\) in (49) does not depend on \(e_{h},\) while \(\tilde{e}_{n}\) in (50) is increasing in \(e_{h}.\) This means that for low values of \(e_{h},\) the binding constraint is \(e_{n}>\bar{e}_{n},\) while for higher values of \(e_{h}\) it is \(e_{n}>\tilde{e}_{n}.\) Table 2 shows how the minimum \(e_{n}\) value changes with \(e_{h}\) for selected values of \(\lambda .\) With \(\lambda =3,\) for instance, \(\bar{e}_{n}=0.708\) while \(\tilde{e}_{n}=0.708\) for \(e_{h}=0.779.\) Thus, for \(0.708<e_{h}<0.779,\) the binding constraint is \(e_{n}> \bar{e}_{n}=0.708.\) For \(e_{h}>0.779,\) the binding constraint is \(e_{n}> \tilde{e}_{n},\) with \(\tilde{e}_{n}\) increasing in \(e_{h}.\) For the maximum value of one for \(e_{h},\) \(\tilde{e}_{n}=0.807.\) For the \(\lambda\) values of 3 and 5, the maximum value of \(e_{h}\) is one, whereas for higher \(\lambda\)’s it is constrained by (48).
Appendix 3: Proofs
1.1 Proof of Proposition 1
Let us first collect the expressions for welfare. Substituting (17) and (19) into (16) yields welfare in scenario \(id,\ i=h,n\):
Substituting (22) and (23) into (21) gives welfare in scenarios nn and nf as:
Substituting (27) and (29) into (26) gives welfare in scenario \(jh,\ j=f,n,\) as:
Before proving the Proposition, we first establish the following two lemmas:
Lemma 1
When the domestic firm has not found the new technology, welfare is higher with free trade than under autarky:\(\ W^{jh}>W^{hd}\) with \(j=f,n.\)
Proof
From (51) with \(i=h\) and (53), it is clear that \(W^{hd}=W^{jh}\) for \(e_{j}=e_{h}.\) From (53):
The sign of \(dW^{jh}/de_{j}\) in (54) is the sign of the numerator on the RHS. Defining \(a\equiv e_{j}/e_{h},\ b\equiv \lambda e_{j}^{2},\) the sign of the numerator is the sign of:
\(\Phi\) has a maximum in b for:
\(b^{*}\) is positive for\(\ a\in (\bar{a};1],\) with \(\bar{a}\approx 0.414.\) For \(a\in \left[ 0;\bar{a}\right] ,\) \(\Phi\) reaches its maximum at \(b=0\), which from (55) is clearly negative.
Substituting \(b=b^{*}\) from (56) into (55), we find the maximum possible value of \(\Phi\) given \(a\in (0.414;1]\):
Plotting this expression shows that \(\Phi ^{*}<0\) for all \(a\in (0.414;1]\). Thus, \(\Phi <0\) in (55) for all feasible values of a and b, which means that \(dW^{jh}/de_{j}<0\) in (54). This combined with \(W^{hd}=W^{jh}\) for \(e_{j}=e_{h}\) proves the lemma. \(\square\)
Lemma 2
In scenario nf with free trade, welfare \(W^{nf}\) net of the domestic upstream firm’s net revenue \(R_{h}^{nf}\) exceeds welfare \(W^{hd}\) in scenario hd under autarky: \(W^{nf}-R_{h}^{nf}>W^{hd}.\)
Proof
Differentiating (57) with respect to \(e_{n}\), we obtain:
with
where \(a\equiv e_{n}/e_{f},\ b\equiv \lambda e_{n}^{2}.\) Note that \(b<\frac{5 }{2}+\frac{3}{2}\sqrt{5}\) by (48).
The sign of the RHS of (58) is the sign of \(\Omega\) which is quadratic in a with a maximum (minimum) for \(b>(<)3.\) The highest value of \(\Omega\) is then at \(\partial \Omega /\partial a=0\) for \(b>3\) (if this is an internal maximum) and at either the highest or lowest value of a for \(b\le 3\). The highest value of a is 1, for which \(\Omega =-2(b+1)<0.\) The lowest value for a is where \(dF_{h}^{nf}/de_{n}=0\) from (25). Substituting this into (59), we find \(\Omega =-2a^{2}b\left( b+1\right) <0.\) For \(b>3,\) the maximum value of \(\Omega\) in (59) occurs at:
Substituting this into (59), the highest possible value of \(\Omega\) is:
We see that \(a^{*}>0\) and \(\Omega ^{*}<0\) for \(b\in \left( 3;2+\sqrt{ 5}\right)\) and \(a^{*}<0\) and \(\Omega ^{*}>0\) for \(b\in \left( 2+ \sqrt{5};\frac{5}{2}+\frac{3}{2}\sqrt{5}\right) .\) Thus, for all values of b for which there is potentially an interior maximum (\(a^{*}>0\)), \(\Omega ^{*}\) is negative. We conclude that \(\Omega\) is negative so that the RHS of (58) is negative. The lowest possible value of \((W^{nf}-F_{h}^{nf})\) is thus achieved at the maximum value of \(e_{n},\) which is \(e_{f}.\) Setting \(e_{n}=e_{f}\) in (57), we find from (51):
The inequality follows from (4) and \(e_{f}<e_{h}.\) \(\square\)
We will now prove Proposition 1 by examining each possible combination of R&D decisions in turn.Footnote 16
1.1.1 No R&D in autarky; (No R&D, No R&D) with trade
In autarky, welfare is \(W^{hd}.\) With trade, welfare is \(W^{fh}.\) By Lemma 1, \(W^{fh}>W^{hd}.\)
1.1.2 No R&D in autarky; (No R&D, R&D) with trade
In autarky, welfare is \(W^{hd}.\) With trade, welfare is \(W^{nh}\) if the foreign firm’s R&D is successful and \(W^{fh}\) if it is not. By Lemma 1, \(W^{jh}>W^{hd},\ j=n,f.\)
1.1.3 No R&D in autarky; (R&D, R&D) with trade
In autarky, welfare is \(W^{hd}.\) With trade, welfare is \(W^{nn}-C^{h}=W^{nf}-C^{h}\) if the domestic firm’s R&D is successful and \(W^{jh}-R,j=f,n,\) if it is not. Thus, we have:Footnote 17
The first inequality follows from \(C^{h}<C_{2}^{h}\) in (R&D, R&D), with \(C_{2}^{h}\) given by (36). The second inequality follows from Lemmas 1 and 2.
1.1.4 R&D in autarky; (No R&D, No R&D) with trade
In autarky, welfare is \(W^{nd}-C^{h}\) if R&D by the domestic firm is successful and \(W^{hd}-C^{h}\) if it is not. With trade, welfare is \(W^{fh}.\) Thus:
Solving for \(p^{h}\), we see that expected welfare under free trade is higher than under autarky if and only if inequality (40) holds.
1.1.5 R&D in autarky; (No R&D, R&D) with trade
In autarky, welfare is \(W^{nd}-C^{h}\) if R&D by the domestic firm is successful and \(W^{hd}-C^{h}\) if it is not. With trade, welfare is \(W^{nh}\) if the foreign firm’s R&D is successful and \(W^{fh}\) if it is not. Thus:
The RHS is positive if and only if (43) holds.
1.1.6 R&D in autarky; (R&D, R&D) with trade
In autarky, welfare is \(W^{nd}-C^{h}\) if R&D by the domestic firm is successful and \(W^{hd}-C^{h}\) if it is not. With trade, welfare is \(W^{nf}-C^{h}=W^{nn}-C^{h}=W^{nd}-C^{h}\) if the domestic firm’s R&D is successful and \(W^{jh}-C^{h},j=f,n,\) if it is not. Thus, we have:
The inequality follows from Lemma 1.
1.2 Proof of Proposition 2
Let us first collect the expressions for emissions. Emissions in each scenario are given by \(e_{1}q_{1}.\) Thus, in scenario \(id,\ i=h,n,\) we have from (19):
In scenarios nf and nn, emissions are, from (23):
In scenario \(jh,\ j=f,n,\) emissions are, from (29):
Before turning to the Proposition, we first establish:
Lemma 3
When the domestic firm has not found the new technology, emissions are higher with free trade than under autarky:\(\ E^{jh}>E^{hd}\) with \(j=f,n.\)
Proof
From (60) and (62), it is clear that \(E^{jh}=E^{hd}\) for \(e_{j}=e_{h}.\) From (62):
Setting \(e_{j}=e_{h}\) yields:
Thus, when reducing \(e_{j}\) below \(e_{h},\) \(E^{jh}\) initially rises above \(E^{hd}.\) However, for lower values of \(e_{j}\), \(E^{jh}\) may decline again.
Defining \(a\equiv e_{j}/e_{h},\ b\equiv \lambda e_{h}^{2},\) we can write ( 62) as:
so that
The (potentially) positive solutions for \(E^{jh}=E^{hd}\) are \(e_{j}=e_{h}\) and
There are only real solutions for a when \(b^{2}-6b+1\ge 0,\) which is satisfied for \(b\le 3-2\sqrt{2}\) and \(b\ge 3+2\sqrt{2}.\) The first inequality is irrelevant by (18). In case the second inequality holds, the highest possible value for a is for the maximum value of b given by (48), combined with the “+” sign on the RHS of (63), so that:
Note that (28) can be written as \(ba^{3}+a-2>0.\) Substituting a from (64) and \(b=\frac{5}{2}+\frac{3}{2}\sqrt{5}\) from (48), we find \(ba^{3}+a-2=0,\) so that (28) is violated. Thus, \(E^{jh}=E^{hd}\) cannot hold and pollution is higher with trade than under autarky. \(\square\)
We will now prove Proposition 2 by examining each possible combination of R&D decisions in turn.Footnote 18
1.2.1 No R&D in autarky; (No R&D, No R&D) with trade
In autarky, emissions are \(E^{hd}\). With trade, emissions are \(E^{fh}.\) By Lemma 3, \(E^{fh}>E^{hd}.\)
1.2.2 No R&D in autarky; (No R&D, R&D) with trade
In autarky, emissions are \(E^{hd}\). With trade, emissions are \(E^{nh}\) if the foreign firm’s R&D is successful and \(E^{fh}\) if it is not. By Lemma 3, \(E^{jh}>E^{hd},\ j=n,f.\)
1.2.3 No R&D in autarky; (R&D, R&D) with trade
In autarky, emissions are \(E^{hd}\). With trade, emissions are \(E^{nn}=E^{nf}\) if the domestic firm’s R&D is successful and \(E^{jh},j=f,n,\) if it is not. We know from Sect. 1 that \(E^{nn}=E^{nf}>E^{hd}\) and from Lemma 3 that \(E^{jh}>E^{hd}\) with \(j=f,n.\)
1.2.4 R&D in autarky; (No R&D, No R&D) with trade
In autarky, emissions are \(E^{nd}\) if R&D is successful and \(E^{hd}\) if it is not. With trade, emissions are \(E^{fh}\) with \(j=f.\) Thus:
Solving for \(p^{h},\) we see that the expected pollution damage under free trade is greater than under autarky if and only if (42) holds.
1.2.5 R&D in autarky; (No R&D, R&D) with trade
In autarky, emissions are \(E^{nd}\) if R&D is successful and \(E^{hd}\) if it is not. With trade, emissions are \(E^{nh}\) if the foreign firm’s R&D is successful and \(E^{fh}\) if it is not. Thus, we have:
By Lemma 3, a sufficient condition for \(D^{NR}>D^{R}\) is (41).
1.2.6 R&D in autarky; (R&D, R&D) with trade
In autarky, emissions are \(E^{nd}\) if R&D is successful and \(E^{hd}\) if it is not. With trade, emissions are \(E^{nn}=E^{nf}=E^{nd}\) if the domestic firm’s R&D is successful and \(E^{jh},j=f,n,\) if it is not. Thus, we have:
The inequality follows from Lemma 3.
About this article
Cite this article
Dijkstra, B.R., Mathew, A.J. Liberalizing trade in environmental goods and services. Environ Econ Policy Stud 18, 499–526 (2016). https://doi.org/10.1007/s10018-015-0121-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10018-015-0121-6