Skip to main content
SpringerLink
Log in

Trajectory generation for balloon robot using time-state control form extended to three dimensions space

  • Original Article
  • Published:
Artificial Life and Robotics Aims and scope Submit manuscript

Abstract

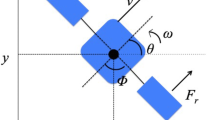
The balloon robot is made up of balloons and has airship-like functions by filling it with helium. Due to the lower risk of accidents compared to other flying robots, balloon robot is better suited for use in densely populated environments. The control characteristics of the balloon robot are that it does not skid and has non-holonomic constraint in the direction perpendicular to the propulsion direction. This makes the balloon robot difficult to control from Brockett's theorem. One of the methods for controlling a robot with non-holonomic constraints is the time-axis state control. In the previous study, predecessor developed a control law for the motion of the balloon robot in two dimensions space. In this study, we extend this control law to three dimensions space by analyzing the relationship between the pitch angle of the balloon robot and the propulsive characteristics of the pectoral fin motion. We analyze the relationship between the pitch angle of the balloon robot and the propulsive characteristics of the pectoral fins and derive the output of translational velocity and turning angular velocity by changing the motion of the pectoral fins in various ways. Based on the results, we simulate the trajectory of the aircraft.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Brockett R, Millman R, Sussman H (1983) Differential geomatric control theory. Springer, pp 181–208

    Google Scholar 

  2. Sampei M (1994) A control strategy for a class of non-holonomic systems—time state control form and its application. In: Proceedings of 33rd, conference on decision and control, pp 1120–1121

  3. Kiyota H, Sampei M (1999) Stabilization of nonholonomic systems without drift terms by time-axis state control form. Trans Inst Syst Control Inf Eng 12:647–654

    Google Scholar 

  4. Yamakawa S (2013) Stabilization condition of chained system based on time-based state control. Trans Soc Instrum Control Eng 49(5):499–504

    Article  Google Scholar 

  5. Miyamae H, Hori K, Uchida M (2021) Control system using time-state control form for balloon robot. IEE J Trans Electr Electron Eng 16:412–418

    Article  Google Scholar 

  6. Miyamae H, Uchida M (2019) Constructing a control system using a time-state control form for a fish-type balloon robot. Artif Life Robot 25:316–321

    Article  Google Scholar 

  7. Haga M, Uchida M (2017) Propulsion modeling of caudal fin driving system on balloon fish robot. Artif Life Robot 22:10–16

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. The Graduate School of Informatics and Engineering, The University of Electro-Communications, 1-5-1 Chofugaoka, Chofu, Tokyo, Japan

    Yusuke Kataoka & Masafumi Uchida

Authors
  1. Yusuke Kataoka
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Masafumi Uchida
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Masafumi Uchida.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kataoka, Y., Uchida, M. Trajectory generation for balloon robot using time-state control form extended to three dimensions space. Artif Life Robotics 27, 506–512 (2022). https://doi.org/10.1007/s10015-022-00757-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10015-022-00757-8

Keywords

Search

Navigation