Multiscale Modelling and Analysis of Signalling Processes in Tissues with Non-Periodic Distribution of Cells

Abstract

In this paper, a microscopic model for a signalling process in the left ventricular wall of the heart, comprising a non-periodic fibrous microstructure, is considered. To derive the macroscopic equations, the non-periodic microstructure is approximated by the corresponding locally periodic microstructure. Then, applying the methods of locally periodic homogenization (the locally periodic (l-p) unfolding operator, locally periodic two-scale (l-t-s) convergence on oscillating surfaces and l-p boundary unfolding operator), we obtain the macroscopic model for a signalling process in the heart tissue.

1 Introduction

In this paper, we consider the multiscale analysis of microscopic problems posed in domains with non-periodic microstructures. We consider a model for a signalling process in the cardiac muscle tissue of the left ventricular wall, comprising plywood-like microstructure [25, 28]. The plywood-like structure is given by the superposition of planes of parallel aligned fibres, gradually rotated with a rotation angle γ, see Fig. 1. In the left ventricular wall, the orientation of the layers of muscle fibres changes from a negative angle at the epicardium to a positive angle at the endocardium. In the microscopic model of a signalling process, we consider the diffusion of signalling molecules in the extracellular space and their interaction with receptors located on the surfaces of muscle cells. There are two main challenges in the multiscale analysis of microscopic problems posed in domains with non-periodic perforations: (i) the approximation of the non-periodic microstructure by a locally periodic one and (ii) derivation of limit equations for the non-linear equations defined on oscillating surfaces of the microstructure. First, assuming the C ²-regularity for the rotation angle γ, we define the locally periodic microstructure which approximates the original non-periodic plywood-like structure. Similar approximation of non-periodic plywood-like microstructure by locally periodic one was considered in [7, 29]. Then, applying techniques of locally periodic homogenization (locally periodic two-scale convergence (l-t-s) and l-p unfolding operator), we derive macroscopic equations for the original microscopic model. The l-p two-scale convergence on oscillating surfaces and l-p boundary unfolding operator allow us to pass to the limit in the non-linear equations defined on surfaces of the locally periodic microstructure.

Fig. 1

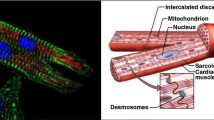
L e f t: Schematic representation of a plywood-like structure. R i g h t: Cardiac muscle fiber orientations vary continuously through the left ventricular wall from a negative angle at the epicardium to positive values toward the endocardium. Republished from A.D. McCulloch, Cardiac biomechanics, in The Biomedical Engineering Handbook, 2nd edn., J.D. Bronzino (ed.), CRC Press, Boca Raton, FL, 2000 [25]

In this paper, we consider a simple model describing the interactions between processes defined in the perforated domain and on the surfaces of the microstructure. However, the techniques presented here can be also applied to more general microscopic models as well as to other non-periodic microstructures, provided the variations in the microscopic structure are sufficiently regular.

Previous results on homogenization in locally periodic media constitute the multiscale analysis of a heat-conductivity problem defined in domains with non-periodically distributed spherical balls [3, 8, 31], and elliptic and Stokes equations in non-periodic fibrous materials [4, 6, 7, 29]. Formal asymptotic expansion and two-scale convergence defined for periodic test functions, [27], were used to derive macroscopic equations for models posed in domains with locally periodic perforations, i.e., domains consisting of periodic cells with smoothly changing perforations [5, 10, 11, 22, 23, 33].

The paper is organized as follows. In Section 2, the microscopic model for a signalling process in a tissue with non-periodic plywood-like microstructure is formulated. In Section 3, we prove the existence and uniqueness results for the microscopic model and derive a priori estimates for a solution of the microscopic model. The approximation of the microscopic equations posed in the domain with non-periodic microstructure by the corresponding problem defined in a domain with locally periodic microstructure is given in Section 4. Then, applying the l-p unfolding operator, l-t-s convergence on oscillating surfaces, and l-p boundary unfolding operator we derive the macroscopic model for a signalling process in the heart muscle tissue. In Appendix, we summarize the definitions and main compactness results for the l-t-s convergence and l-p unfolding operator.

2 Microscopic Model for a Signalling Process in Heart Tissue

In this work, we consider a receptor-based microscopic model for a cellular signalling process in cardiac tissue. A signalling system is important for proper function of cells and appropriate respond to changes in the extracellular environment. Many regulatory events in cardiac tissue are mediated via surface receptors, located in cardiac cells membrane, that transmit signals through the activation of GTP binding proteins (G proteins) [34]. Cardiac cells (myocytes) in the heart wall tissue are joined in a linear arrangement to form muscle fibres. In the left ventricular wall of the heart the orientation of layers of muscle fibre changes with position through the wall. The layers of parallel aligned muscle fibres are rotated from −60^∘ at epicardium to +70^∘ at endocardium [25] and create a non-periodic plywood-like microstructure. For simplicity, we assume that the individual muscle fibres are not connected to each other. However, it is possible to consider a periodic distribution of connections between the fibres.

In the mathematical model for a signalling process in cardiac tissue, we consider the binding of signalling molecules to receptors located on the cell membrane, which through the activation of G proteins (not considered in our simple model) results in the activation of a cell signalling pathway. We consider the diffusion, production and decay of ligands (signalling molecules) c and binding of ligands to the membrane receptors. We shall distinguish between free receptors r _f and bound receptors r _b , which correspond to receptor-ligand complexes. We assume that the receptor-ligand complex can dissociate and result in a free receptor and ligand. We also consider the production of new free receptors and natural decay of free and bound receptors.

$$\begin{array}{llll} &\partial_{t} c - \nabla\cdot (A(x) \nabla c) = F(x,c) && \text{ in the extracellular space}, \\ &A(x) \nabla c \cdot n = - \alpha(x) c\, r_{f} + \beta(x) r_{b} && \text{ on the cell membrane}, \\ &\partial_{t} r_{f} = p(x, r_{b}) - \alpha(x) c\, r_{f} + \beta(x) r_{b} - d_{f}(x) r_{f} && \text{ on the cell membrane}, \\ &\partial_{t} r_{b} = \alpha(x) c\, r_{f} - \beta(x) r_{b} - d_{b}(x) r_{b} && \text{ on the cell membrane}, \end{array} $$

where d _f and d _b are the decay rates, β denotes the dissociation rate for the receptor-ligand complex, α is the binding rate, the function p models the production of free receptors, and the function F describes the production and decay of ligands.

To define the plywood-like microstructure of the cardiac muscle tissue of the left ventricular wall, we consider a function $\gamma \in C^{2}(\mathbb R)$, with −π/2≤γ(x)≤π/2 for $x\in \mathbb R$ and define the rotation matrix around the x ₃-axis as

$$R(\gamma(x)) = \left(\begin{array}{ccc} \cos(\gamma(x)) &\quad- \sin(\gamma(x))&\quad 0\\ \sin(\gamma(x)) &\quad \cos(\gamma(x))&\quad 0\\ 0 &\quad 0 &\quad 1 \end{array} \right), $$

where γ(x) denotes the rotation angle with the x ₁-axis. Denote R _x : = R(γ(x ₃)).

We consider an open, bounded subdomain ${\Omega }\subset \mathbb R^{3}$, with Lipschitz boundary, representing a part of the cardiac muscle tissue and the x ₃-axis to be orthogonal to the layers of parallel-aligned muscle fibres. We assume that the radius of the muscle fibres depends on the position in the tissue and define the characteristic function of a fibre by

$$\vartheta(x, y)=\left\{ \begin{array}{ll} 1, \quad& |\hat y|\leq \rho(\hat x_{R}) a,\\ 0, \quad& |\hat y|>\rho(\hat x_{R}) a, \end{array}\right. $$

where $\hat y = (y_{2}, y_{3})$ and $\hat x_{R} = ((R_{x}^{-1} x)_{2}, (R_{x}^{-1}x)_{3})$, $\rho \in C^{1}(\mathbb R^{2})$, with $0< \rho _{0} \leq \rho (\hat x_{R}) \leq \rho _{1} < \infty$ and $\rho (\hat x_{R})a\leq 2/5$ for all $x\in \overline {\Omega }$, i.e., a=2/(5ρ ₁).

By small parameter ε we denote the characteristic size of the microstructure of cardiac tissue, given as a ratio between the characteristic diameter of muscle fibres and characteristic size of the cardiac tissue. Notice that for plywood-like microstructure the axis of each fibre can be defined by a rotated around the x ₃-axis line, parallel to the x ₁-axis and passing through a point of an ε-grid in the plane x ₁=const. Thus, for $j\in \mathbb Z^{3}$, we define $x_{j}^{\varepsilon }=R_{x_{j}^{\varepsilon }} \varepsilon j$ with $R_{x_{j}^{\varepsilon }}:= R(\gamma (x_{j,3}^{\varepsilon }))$. Notice that $x_{j,3}^{\varepsilon } =\varepsilon j_{3}$ and the third variable is invariant under the rotation $R_{x_{j}^{\varepsilon }}$. This ensures that for each fixed ε j ₃ we obtain a layer of parallel aligned fibres.

Then the perforated domain ${\Omega }_{\varepsilon }^{\ast }$, corresponding to the extracellular space of cardiac tissue, is defined as

$${\Omega}^{\ast}_{\varepsilon} = {\Omega} \setminus {\Omega}_{\varepsilon}^{0}, \quad \text{ with} \,\,\, {\Omega}_{\varepsilon}^{0} = \bigcup_{j \in {\Xi}_{\varepsilon}} (\varepsilon R_{x_{j}^{\varepsilon}} K_{x_{j}^{\varepsilon}} Y_{0}+ x_{j}^{\varepsilon}) = \bigcup_{j \in {\Xi}_{\varepsilon}} \varepsilon R_{x_{j}^{\varepsilon}} (K_{x_{j}^{\varepsilon}}Y_{0}+ j), $$

where ${\Xi }_{\varepsilon } = \{j \in \mathbb Z^{3}: \varepsilon R_{x_{j}^{\varepsilon }} (\overline Y_{1}+ j) \subset {\Omega }\}$, $Y_{0}=\{ y\in \overline Y_{1}: |\hat y| \leq a\}$, with a=2/(5ρ ₁) and $\rho _{1}=\sup _{\overline {\Omega }} \rho (x)$, and

$$Y_{1}= \left(-\frac12,\frac12\right)^{3}, \quad K_{x} = K(x), \quad K(x) = \begin{pmatrix} 1\; & 0&0\\ 0\; & \rho(\hat x_{R}) & 0 \\ 0\; & 0& \rho(\hat x_{R}) \end{pmatrix}. $$

We aslo define $Y_{x_{j}^{\varepsilon }} = R_{x_{j}^{\varepsilon }} Y_{1}$, and $Y^{\ast }_{x_{j}^{\varepsilon }, K} = R_{x_{j}^{\varepsilon }} (Y_{1}\setminus K_{x_{j}^{\varepsilon }} Y_{0})$ for j∈Ξ _ε .

We denote ${\Gamma }_{0,1} =\{y \in \mathbb R^{3}: \; y_{1} = \pm 1/2 \}$. Then, assumptions on ρ and a ensure that K _x (Y ₀∖Γ_0,1)⊂Y ₁ for all $x\in \overline {\Omega }$ and, since R is a rotation matrix, $(\varepsilon R_{x_{n}^{\varepsilon }} K_{x_{n}^{\varepsilon }} Y_{0} + x_{n}^{\varepsilon })\cap (\varepsilon R_{x_{m}^{\varepsilon }} K_{x_{m}^{\varepsilon }} Y_{0} + x_{m}^{\varepsilon }) = \emptyset$ for any m,n∈Ξ _ε with n ₂≠m ₂ or n ₃≠m ₃. Hence, ${\Omega }_{\varepsilon }^{\ast }$ is connected. This corresponds to our assumption that muscle fibres do not touch each other and are not directly connected, and the interactions between the muscle fibres are facilitated through the extracellular matrix.

Now, using the definition of 𝜗, the characteristic function of muscle fibres in cardiac tissue reads

$$ \chi_{{\Omega}_{f}^{\varepsilon}} (x) =\chi_{\Omega}(x)\sum\limits_{j\in {\Xi}_{\varepsilon}} \vartheta \left(x_{j}^{\varepsilon}, R^{-1}_{x_{j}^{\varepsilon}}(x- x_{j}^{\varepsilon})/ \varepsilon\right) $$

and the extracellular space is characterised by

$$\chi_{{\Omega}^{\ast}_{\varepsilon}} = (1 - \chi_{{\Omega}^{\varepsilon}_{f}})\chi_{\Omega}. $$

The surfaces of muscle cells, i.e., the boundaries of the microstructure, are denoted by

$${\Gamma}^{\varepsilon} = \sum\limits_{j \in {\Xi}_{\varepsilon}} \left(\varepsilon R_{x_{j}^{\varepsilon}} K_{x_{j}^{\varepsilon}}{\Gamma} + x_{j}^{\varepsilon}\right)= \sum\limits_{j \in {\Xi}_{\varepsilon}} \varepsilon R_{x_{j}^{\varepsilon}} (K_{x_{j}^{\varepsilon}}{\Gamma} + j), $$

where ${\Gamma } =\overline {\partial Y_{0}\setminus {\Gamma }_{0,1}}$.

Notice that the changes in the microstructure of ${\Omega }^{\ast }_{\varepsilon }$ are defined by changes in the periodicity given by the linear transformation (rotation) R(x) and by changes in the shape of the microstructure (changes in the radius of muscle fibres) given by the linear transformation K(x) for x∈Ω.

To determine the non-constant reaction rates for binding and dissociation processes on cell membranes, we consider $\alpha , \beta \in C^{1}(\overline {\Omega }; {C^{1}_{0}}(Y_{1}))$, extended in y-variable by zero to $\mathbb R^{3}$, and define

$$\begin{array}{@{}rcl@{}} \alpha^{\varepsilon}(x)&=& \sum\limits_{j \in {\Xi}_{\varepsilon}} \alpha(x, R^{-1}_{x_{j}^{\varepsilon}}(x-x_{j}^{\varepsilon})/\varepsilon)\chi_{(\varepsilon Y_{x_{j}^{\varepsilon}} + x_{j}^{\varepsilon})}(x), \\ \beta^{\varepsilon}(x)&=& \sum\limits_{j \in {\Xi}_{\varepsilon}}\beta(x, R^{-1}_{x_{j}^{\varepsilon}}(x-x_{j}^{\varepsilon})/\varepsilon)\chi_{(\varepsilon Y_{x_{j}^{\varepsilon}} + x_{j}^{\varepsilon})}(x). \end{array} $$

Then, the microscopic model for a signalling process in cardiac tissue reads

$$ \begin{array}{rll} \partial_{t} c^{\varepsilon} - \text{div}(A \nabla c^{\varepsilon}) &= F(c^{\varepsilon})& \text{ in}\,\, (0,T)\times {\Omega}^{\ast}_{\varepsilon}, \\ -A \nabla c^{\varepsilon} \cdot \textbf{n} & =\varepsilon \left[\alpha^{\varepsilon}(x) \, c^{\varepsilon} \, r_{f}^{\varepsilon} - \beta^{\varepsilon}(x)\, r_{b}^{\varepsilon} \right]& \text{ on}\,\, (0,T)\times {\Gamma}^{\varepsilon}, \\ A \nabla c^{\varepsilon} \cdot \textbf{n} &= 0 & \text{ on}\,\, (0,T)\times(\partial{\Omega}^{\ast}_{\varepsilon}\setminus {\Gamma}^{\varepsilon}),\\ c^{\varepsilon}(0,x) &= c_{0}(x) & \text{ in}\,\, {\Omega}^{\ast}_{\varepsilon}, \end{array} $$

(1)

where the dynamics in the concentrations of free and bound receptors on cell surfaces is determined by two ordinary differential equations

$$ \begin{array}{rll} \partial_{t} r^{\varepsilon}_{f} &= p(r_{b}^{\varepsilon}) - \alpha^{\varepsilon}(x) c^{\varepsilon} r_{f}^{\varepsilon} + \beta^{\varepsilon}(x) r_{b}^{\varepsilon} -d_{f} r_{f}^{\varepsilon} \quad & \text{ on} \, (0,T)\times {\Gamma}^{\varepsilon},\\ \partial_{t} r^{\varepsilon}_{b} &= \alpha^{\varepsilon}(x) c^{\varepsilon} r_{f}^{\varepsilon} - \beta^{\varepsilon}(x) r_{b}^{\varepsilon} - d_{b} r_{b}^{\varepsilon} \quad & \text{ on} \, (0,T)\times {\Gamma}^{\varepsilon}, \\ r_{f}^{\varepsilon}(0, x) &= r_{f0}^{\varepsilon}(x), \quad \qquad r_{b}^{\varepsilon}(0, x) = r_{b0}^{\varepsilon}(x) \quad & \text{ on} \, {\Gamma}^{\varepsilon}, \end{array} $$

(2)

with initial conditions defined as

$$r_{l0}^{\varepsilon}(x)= r_{l0}^{1}(x) \sum\limits_{j \in {\Xi}_{\varepsilon}} r_{l0}^{2}(R_{x_{j}^{\varepsilon}}^{-1} (x- x_{j}^{\varepsilon})/\varepsilon) \chi_{(\varepsilon Y_{x_{j}^{\varepsilon}} + x_{j}^{\varepsilon})}(x) \qquad \text{ for} \; l=f,b. $$

For simplicity of the presentation we shall assume that the diffusion coefficient A and the decay rates d _f , d _b are constant. We also assume that the functions F and p are independent of x∈Ω. The dependence of A, d _f , d _b , F and p on the microscopic and macroscopic variables can be analyzed in the similar way as for α ^ε and β ^ε.

Assumption 1

• A is symmetric and (A ξ,ξ)≥a ₀|ξ|² for $\xi \in \mathbb R^{3}$, a ₀>0.

• $\gamma \in C^{2}(\mathbb R)$, $K \in C^{1}(\overline {\Omega })$ with $0< {\rho _{0}^{2}} \leq |\det K(x)| \leq {\rho _{1}^{2}}< \infty$ and K(x)(Y ₀∖Γ_0,1)⊂Y ₁ for all $x\in \overline {\Omega }$, and d _l ≥0 for l = f,b.

• $F:\mathbb R\to \mathbb R$ is Lipschitz continuous, F(ξ ₋)ξ ₋≤μ _F |ξ ₋|², with μ _F >0 and ξ ₋= min{0,ξ}.

• $p: \mathbb R \to \mathbb R$ is Lipschitz continuous and p(ξ)≥0 for ξ≥0.

• $\alpha , \beta \in C^{1}(\overline {\Omega }; {C_{0}^{1}}(Y_{1}))$ are nonnegative.

• c ₀∈H ¹(Ω)∩L ^∞(Ω), $r^{1}_{l0} \in C^{1}(\overline {\Omega })$, and $r^{2}_{l0} \in {C^{1}_{0}}(Y_{1})$, extended by zero to $\mathbb R^{3}$, and c ₀, $r^{j}_{l0}$ are nonnegative for l = f,b and j=1,2.

Notice that the C ¹-regularity of α and β is required for the approximation of the integrals defined on the boundaries of the non-periodic microstructure by the integrals defined on the boundaries of the corresponding locally periodic microstructure.

We shall use the following notations ${\Omega }_{\varepsilon , T}^{\ast } = (0,T)\times {\Omega }_{\varepsilon }^{\ast }$ ${\Gamma }^{\varepsilon }_{T} = (0,T)\times {\Gamma }^{\varepsilon }$, Ω _T =(0,T)×Ω, Γ _T =(0,T)×Γ, and Γ _x,T =(0,T)×Γ _x .

For u∈L ^q(0,τ;L ^p(G)) and $v \in L^{q^{\prime }}(0,\tau ; L^{p^{\prime }} (G))$, with 1/p+1/p ^′=1 and 1/q+1/q ^′=1, τ>0 and $G \subset \mathbb {R}^{d}$ for d=2 or 3, we denote $\langle u,v \rangle _{G_{\tau }} = {\int }_{0}^{\tau }{\int }_{G} uvdx dt$.

We shall consider a weak solution of the problem (1) and (2), defined in the following way.

Definition 1

A weak solution of the microscopic problem (1) and (2) are functions c ^ε, $r^{\varepsilon }_{f}$, $r^{\varepsilon }_{b}$ such that

$$\begin{array}{@{}rcl@{}} c^{\varepsilon} &\in& L^{2}(0,T; H^{1}({\Omega}^{\ast}_{\varepsilon}))\cap H^{1}(0,T; L^{2}({\Omega}_{\varepsilon}^{\ast})), \\ r_{l}^{\varepsilon} &\in& H^{1}(0,T; L^{2}({\Gamma}^{\varepsilon})),\quad r_{l}^{\varepsilon} \in L^{\infty}(0,T; L^{\infty}({\Gamma}^{\varepsilon})), \quad l = f,b, \end{array} $$

satisfying (1) in the weak form

$$ \langle \partial_{t} c^{\varepsilon}, \phi \rangle_{{\Omega}_{\varepsilon, T}^{\ast}} + \langle A\nabla c^{\varepsilon}, \nabla \phi \rangle_{{\Omega}_{\varepsilon, T}^{\ast}} = \langle F(c^{\varepsilon}), \phi \rangle_{{\Omega}_{\varepsilon,T}^{\ast}} + \varepsilon \langle \beta^{\varepsilon} r^{\varepsilon}_{b} - \alpha^{\varepsilon} c^{\varepsilon} r^{\varepsilon}_{f}, \phi \rangle_{{\Gamma}^{\varepsilon}_{T}} $$

(3)

for all $\phi \in L^{2}(0,T; H^{1}({\Omega }_{\varepsilon }^{\ast }))$, (2) are satisfied a.e. on ${\Gamma }^{\varepsilon }_{T}$, and c ^ε→c ₀ in $L^{2}({\Omega }_{\varepsilon }^{\ast })$, $r_{l}^{\varepsilon } \to r_{l0}^{\varepsilon }$ in L ²(Γ^ε) for l = f,b, as t→0.

3 Existence, Uniqueness, and a Priori Estimates for a Weak Solution of the Microscopic Problem (1) and (2)

In a similar way as in [9, 21, 30], we can prove the existence, uniqueness, and a priori estimates for a weak solution of problem (1)–(2). Notice that for the derivation of a priori estimates a trace estimate, uniform in ε, for functions $\phi \in W^{1,p}({\Omega }^{\ast }_{\varepsilon })$ is required. The fact that K _x (Y ₀∖Γ_0,1)⊂Y ₁ for all $x\in \overline {\Omega }$ and the uniform boundedness of detK, i.e., $0<{\rho ^{2}_{0}} \leq |\det K(x)|\leq {\rho ^{2}_{1}} < \infty$, ensure the trace estimate for $\phi \in H^{1}(Y_{1}\setminus K_{x_{j}^{\varepsilon }} Y_{0})$, i.e.,

$$\|\phi \|^{p}_{L^{p}(K_{x_{j}^{\varepsilon}}{\Gamma})} \leq C \left[\|\phi\|^{p}_{L^{p}(Y_{1}\setminus K_{x_{j}^{\varepsilon}} Y_{0})} + \|\nabla_{y} \phi\|^{p}_{L^{p}(Y_{1}\setminus K_{x_{j}^{\varepsilon}} Y_{0})}\right], $$

where the constant C depends on Y ₁, Y ₀, K and is independent of ε and j∈Ξ _ε . Then, considering the change of variables $x= \varepsilon R_{x_{j}^{\varepsilon }} y + x_{j}^{\varepsilon } = \varepsilon R_{x_{j}^{\varepsilon }} (y + j)$ and summing up over j∈Ξ _ε , we obtain for $\phi \in W^{1,p}({\Omega }^{\ast }_{\varepsilon })$, with p∈[1,∞), that

$$ \varepsilon \| \phi \|^{p}_{L^{p}({\Gamma}^{\varepsilon})} \leq \tilde \mu \left[\| \phi \|^{p}_{L^{p}({\Omega}_{\varepsilon}^{\ast})} + \varepsilon^{p} \|\nabla \phi \|^{p}_{L^{p}({\Omega}_{\varepsilon}^{\ast})} \right], $$

(4)

where the constant $\tilde \mu$ depends on Y ₁, Y ₀, R and K and is independent of ε.

Lemma 1

Under Assumption 1 there exists a unique non-negative weak solution of the microscopic problem (1) and (2) satisfying the following a priori estimates

$$\begin{array}{@{}rcl@{}} \|c^{\varepsilon}\|_{L^{\infty}(0,T; L^{2}({\Omega}_{\varepsilon}^{\ast}))} + \|\nabla c^{\varepsilon}\|_{L^{2}({\Omega}_{\varepsilon, T}^{\ast})} + \|\partial_{t} c^{\varepsilon}\|_{L^{2}({\Omega}_{\varepsilon,T}^{\ast})} + \varepsilon^{\frac 12} \|c^{\varepsilon}\|_{L^{2}({\Gamma}^{\varepsilon}_{T})} &\leq& \mu, \end{array} $$

(5a)

$$\begin{array}{@{}rcl@{}} \|r^{\varepsilon}_{f}\|_{L^{\infty}({\Gamma}^{\varepsilon}_{T})} + \|r^{\varepsilon}_{b}\|_{L^{\infty}({\Gamma}^{\varepsilon}_{T})} + \varepsilon^{\frac 12}\|\partial_{t} r^{\varepsilon}_{f}\|_{L^{2}({\Gamma}^{\varepsilon}_{T})} + \varepsilon^{\frac 12}\|\partial_{t} r^{\varepsilon}_{b}\|_{L^{2}({\Gamma}^{\varepsilon}_{T})} &\leq& \mu, \end{array} $$

(5b)

and

$$ \|(c^{\varepsilon}-M_{1} e^{M_{2} t})^{+}\|_{L^{\infty}(0,T; L^{2}({\Omega}_{\varepsilon}^{\ast}))} + \|\nabla (c^{\varepsilon}-M_{1} e^{M_{2} t})^{+}\|_{L^{2}({\Omega}_{\varepsilon, T}^{\ast})} \leq \mu\, \varepsilon, $$

(6)

where the constant μ is independent of ε, $M_{1} \geq \|c_{0}\|_{L^{\infty }({\Omega })}$ , and $M_{1}M_{2} \geq |F(0)| + \|F^{\prime }\|_{L^{\infty }}M_{1} + \tilde \mu \|\beta \|_{L^{\infty }({\Omega }\times Y_{1})} \|r_{b}^{\varepsilon }\|_{L^{\infty }({\Gamma }^{\varepsilon }_{T})}$ , with $\tilde \mu$ being the constant in the trace inequality (4).

Proof

(Sketch) As in [30] the existence of a solution of the microscopic problem (1) and (2) for each fixed ε>0 is obtained by applying fixed point arguments and Galerkin method. Also, using the same arguments as in [30] we obtain that c ^ε(t,x)≥0 for $(t,x) \in {\Omega }_{\varepsilon , T}^{\ast }$ and $r^{\varepsilon }_{l} (t,x) \geq 0$ for $(t,x) \in {\Gamma }_{T}^{\varepsilon }$, with l = f,b. To derive a priori estimates, we consider the structure of the microscopic equations. For non-negative solutions, by adding the equations for $r_{f}^{\varepsilon }$ and $r_{b}^{\varepsilon }$, we obtain

$$\partial_{t} (r_{f}^{\varepsilon}+ r_{b}^{\varepsilon}) = p(r_{b}^{\varepsilon}) - d_{b} r_{b}^{\varepsilon} -d_{f} r_{f}^{\varepsilon}. $$

Then the Lipschitz continuity of p and the non-negativity of $r_{f}^{\varepsilon }$ and $r_{b}^{\varepsilon }$ imply the boundedness of $r_{f}^{\varepsilon }$ and $r_{b}^{\varepsilon }$ on ${\Gamma }^{\varepsilon }_{T}$.

Considering c ^ε as a test function in (3) and using the trace inequality (4), we obtain the estimates for c ^ε. Testing (2) by $\partial _{t} r_{f}^{\varepsilon }$ and $\partial _{t} r_{b}^{\varepsilon }$, respectively, yields the estimates for the time derivatives of $r_{f}^{\varepsilon }$ and $r_{b}^{\varepsilon }$. In the derivation of the a priori estimate for ∂ _t c ^ε we use the equation for $\partial _{t} r_{f}^{\varepsilon }$ to estimate the non-linear term on the boundary Γ^ε, i.e.,

$$\begin{array}{@{}rcl@{}} &&-{\int}_{{\Gamma}^{\varepsilon}} \alpha^{\varepsilon}(x) r^{\varepsilon}_{f} \, c^{\varepsilon} \partial_{t} c^{\varepsilon} d\sigma_{x} = -\frac 12 \frac{d}{dt}{\int}_{{\Gamma}^{\varepsilon}} \alpha^{\varepsilon}(x) r^{\varepsilon}_{f} \, |c^{\varepsilon} |^{2} d\sigma_{x} \\ &&\qquad\qquad + \frac 12 {\int}_{{\Gamma}^{\varepsilon}} \alpha^{\varepsilon}(x) (p(r_{b}^{\varepsilon}) - \alpha^{\varepsilon}(x) r_{f}^{\varepsilon} c^{\varepsilon} + \beta^{\varepsilon}(x) r_{b}^{\varepsilon} - d_{f} r_{f}^{\varepsilon}) |c^{\varepsilon}|^{2} d\sigma_{x} \\ &&\qquad\qquad \leq \frac 12 {\int}_{{\Gamma}^{\varepsilon}} \left(\alpha^{\varepsilon}(x) p(r_{b}^{\varepsilon}) + \beta^{\varepsilon}(x) r_{b}^{\varepsilon}\right) |c^{\varepsilon}|^{2} d\sigma_{x} - \frac 12 \frac{d}{dt}{\int}_{{\Gamma}^{\varepsilon}} \alpha^{\varepsilon}(x) r^{\varepsilon}_{f} \, |c^{\varepsilon} |^{2} d\sigma_{x}. \end{array} $$

Considering $(c^{\varepsilon } - M_{1} e^{M_{2} t})^{+}$ as a test function in (3), where M ₁ and M ₂ are as in the formulation of the lemma, we obtain

$$\begin{array}{@{}rcl@{}} && {\int}_{{\Omega}_{\varepsilon}^{\ast}} |(c^{\varepsilon}(\tau) - M_{1}e^{M_{2} \tau})^{+}|^{2} dx + {\int}_{0}^{\tau} {\int}_{{\Omega}_{\varepsilon}^{\ast}} M_{1} M_{2}e^{M_{2} t} (c^{\varepsilon} - M_{1}e^{M_{2} t})^{+} dx dt \\ && + {\int}_{0}^{\tau} \left[{\int}_{{\Omega}_{\varepsilon}^{\ast}} |\nabla (c^{\varepsilon} - M_{1} e^{M_{2} t})^{+}|^{2} dx + \varepsilon {\int}_{{\Gamma}^{\varepsilon}} \alpha^{\varepsilon}(x) r^{\varepsilon}_{f} c^{\varepsilon} (c^{\varepsilon}-M_{1} e^{M_{2} t})^{+} d\sigma_{x} \right] dt \\ &&\leq C_{1} {\int}_{0}^{\tau} \left[{\int}_{{\Omega}_{\varepsilon}^{\ast}} F(c^{\varepsilon}) (c^{\varepsilon} - M_{1}e^{M_{2} t})^{+} dx + \varepsilon {\int}_{{\Gamma}^{\varepsilon}} \beta^{\varepsilon}(x) r_{b}^{\varepsilon} (c^{\varepsilon} - M_{1}e^{M_{2} t})^{+} d\sigma_{x} \right]dt \end{array} $$

for τ∈(0,T]. Using the non-negativity and boundedness of β ^ε and $r_{f}^{\varepsilon }$, along with the trace inequality (4), the last integral can be estimated as

$$\begin{array}{@{}rcl@{}} &&\varepsilon {\int}_{0}^{\tau} {\int}_{{\Gamma}^{\varepsilon}} \beta^{\varepsilon} r_{b}^{\varepsilon} (c^{\varepsilon} - M_{1}e^{M_{2} t})^{+} d\sigma_{x} dt\\ && \leq \mu_{1} {\int}_{0}^{\tau} {\int}_{{\Omega}_{\varepsilon}^{\ast}} (c^{\varepsilon} - M_{1}e^{M_{2} t})^{+} dx dt + \varepsilon \mu_{1} {\int}_{0}^{\tau} {\int}_{{\Omega}_{\varepsilon}^{\ast}} |\nabla (c^{\varepsilon} - M_{1}e^{M_{2} t})^{+}| dx dt\\ &&\leq \mu_{1} {\int}_{0}^{\tau} {\int}_{{\Omega}_{\varepsilon}^{\ast}} (c^{\varepsilon} - M_{1}e^{M_{2} t})^{+} dx dt + \mu_{2} \delta {\int}_{0}^{\tau} {\int}_{{\Omega}_{\varepsilon}^{\ast}} |\nabla (c^{\varepsilon} - M_{1}e^{M_{2} t})^{+}|^{2} dx dt + \mu_{\delta} \varepsilon^{2} \end{array} $$

for any δ>0, where the constants μ ₁, μ ₂ and μ _δ depend on $\|\beta \|_{L^{\infty }({\Omega }\times Y_{1})}$, $\|r_{b}^{\varepsilon }\|_{L^{\infty }({\Gamma }^{\varepsilon }_{T})}$ and on the transformation matrices R and K, but are independent of ε. More specifically, $\mu _{1} = \tilde \mu \|\beta \|_{L^{\infty }({\Omega }\times Y_{1})}\|r_{b}^{\varepsilon }\|_{L^{\infty }({\Gamma }^{\varepsilon }_{T})}$. Using the non-negativity of c ^ε and $r^{\varepsilon }_{f}$, the Lipschitz continuity of F, and the assumptions on M ₁ and M ₂, and applying the Gronwall inequality yield estimate (6).

To show the uniqueness of a solution of the microscopic problem (1) and (2), we consider the equations for the difference of two solutions $(c^{\varepsilon }_{1}, r^{\varepsilon }_{f,1}, r^{\varepsilon }_{b,1})$ and $(c^{\varepsilon }_{2}, r^{\varepsilon }_{f,2}, r^{\varepsilon }_{b,2})$. The non-negativity of α ^ε, $r^{\varepsilon }_{f,j}$, and $c^{\varepsilon }_{j}$, along with the boundedness of $r^{\varepsilon }_{f,j}$, ensures

$$\|r^{\varepsilon}_{f,1}(\tau) - r^{\varepsilon}_{f,2}(\tau)\|^{2}_{L^{2}({\Gamma}^{\varepsilon})} \leq \mu {\int}_{0}^{\tau} \left[\sum\limits_{l=f,b}\|r^{\varepsilon}_{l,1} - r^{\varepsilon}_{l,2}\|^{2}_{L^{2}({\Gamma}^{\varepsilon})} + \|c^{\varepsilon}_{1} - c^{\varepsilon}_{2}\|^{2}_{L^{2}({\Gamma}^{\varepsilon})} \right] dt. $$

Testing the sum of the equations for $r^{\varepsilon }_{f,1} -r^{\varepsilon }_{f,2}$ and $r^{\varepsilon }_{b,1}- r^{\varepsilon }_{b,2}$ by $r^{\varepsilon }_{f,1} + r^{\varepsilon }_{b,1}- r^{\varepsilon }_{f,2} - r^{\varepsilon }_{b,2}$ and using the estimate from above yield

$$\begin{array}{@{}rcl@{}} \|r^{\varepsilon}_{b,1}(\tau) - r^{\varepsilon}_{b,2}(\tau)\|^{2}_{L^{2}({\Gamma}^{\varepsilon})} &\leq& \|r^{\varepsilon}_{b,1}(\tau) + r^{\varepsilon}_{f,1}(\tau)- r^{\varepsilon}_{b,2}(\tau) - r^{\varepsilon}_{f,2}(\tau)\|^{2}_{L^{2}({\Gamma}^{\varepsilon})} \\ &&+ \|r^{\varepsilon}_{f,1}(\tau) - r^{\varepsilon}_{f,2}(\tau)\|^{2}_{L^{2}({\Gamma}^{\varepsilon})} \\ &\leq& \mu_{1}{\int}_{0}^{\tau} \sum\limits_{l=f,b} \|r^{\varepsilon}_{l,1} \!- r^{\varepsilon}_{l,2}\|^{2}_{L^{2}({\Gamma}^{\varepsilon})} dt \,+\, \mu_{2}{\int}_{0}^{\tau} \|c^{\varepsilon}_{1} - c^{\varepsilon}_{2}\|^{2}_{L^{2}({\Gamma}^{\varepsilon})} dt. \end{array} $$

Combining the last two inequalities and applying the Gronwall inequality imply the estimates for $\|r^{\varepsilon }_{l,1}(\tau ) - r^{\varepsilon }_{l,2}(\tau )\|^{2}_{L^{2}({\Gamma }^{\varepsilon })}$, with l = f,b, in terms of $\|c^{\varepsilon }_{1} - c^{\varepsilon }_{2}\|^{2}_{L^{2}((0,\tau )\times {\Gamma }^{\varepsilon })}$ for τ∈(0,T].

Considering (c ^ε−S)⁺, with some S>0, as a test function in (3) and using the boundedness of $r^{\varepsilon }_{f}$ and $r^{\varepsilon }_{b}$ we obtain

$$\|(c^{\varepsilon} - S)^{+}\|_{L^{\infty}(0,T; L^{2}({\Omega}_{\varepsilon}^{\ast}))} + \|\nabla(c^{\varepsilon} - S)^{+}\|_{L^{2}({\Omega}_{\varepsilon, T}^{\ast})} \leq \mu_{1} S \left({{\int}_{0}^{T}} |{\Omega}_{\varepsilon}^{\ast,S}(t) | dt \right)^{\frac 12}, $$

where $S\geq \max \{\|c_{0}\|_{L^{\infty }({\Omega })}, \|\beta \|_{L^{\infty }({\Omega }\times Y_{1})}\|r_{b}^{\varepsilon }\|_{L^{\infty }({\Gamma }_{T}^{\varepsilon })}, |F(0)| \}$, μ ₁ is some positive constant, and ${\Omega }_{\varepsilon }^{\ast , S}(t) = \{ x\in {\Omega }_{\varepsilon }^{\ast } : c^{\varepsilon }(t,x) >S\}$. Then, Theorem II.6.1 in [20] yields the boundedness of c ^ε in $(0,T)\times {\Omega }_{\varepsilon }^{\ast }$ for every fixed ε.

Considering now (3) for two solutions $(c^{\varepsilon }_{1}, r_{f,1}^{\varepsilon }, r_{b,1}^{\varepsilon })$ and $(c^{\varepsilon }_{2}, r_{f,2}^{\varepsilon }, r_{b,2}^{\varepsilon }),$ we obtain the estimates for $\|c_{1}^{\varepsilon } - c_{2}^{\varepsilon }\|^{2}_{L^{2}({\Omega }^{\ast }_{\varepsilon , \tau })}$ and $\varepsilon \|c_{1}^{\varepsilon } - c_{2}^{\varepsilon }\|^{2}_{L^{2}((0,\tau )\times {\Gamma }^{\varepsilon })}$ in terms of $\varepsilon \|r^{\varepsilon }_{l,1} - r^{\varepsilon }_{l,2}\|^{2}_{L^{2}((0,\tau )\times {\Gamma }^{\varepsilon })}$, with l = f,b and τ∈(0,T]. Using the estimates for $\|r^{\varepsilon }_{l,1}(\tau ) - r^{\varepsilon }_{l,2}(\tau )\|^{2}_{L^{2}({\Gamma }^{\varepsilon })}$ in terms of $\|c_{1}^{\varepsilon } - c_{2}^{\varepsilon }\|^{2}_{L^{2}((0,\tau )\times {\Gamma }^{\varepsilon })}$, shown above, and applying the Gronwall inequality, we conclude that $r^{\varepsilon }_{l,1} = r^{\varepsilon }_{l,2}$ on (0,T)×Γ^ε, with l = f,b, and $c^{\varepsilon }_{1}= c^{\varepsilon }_{2}$ in $(0,T)\times {\Omega }^{\ast }_{\varepsilon }$. □

The assumptions on the non-periodic microstructure of ${\Omega }_{\varepsilon }^{\ast }$ and the regularity of the transformation matrices R and K ensure the following extension result.

Lemma 2

For $x_{j}^{\varepsilon } \in {\Omega }$ , and $u \in W^{1,p}(Y^{\ast }_{x_{j}^{\varepsilon }, K})$ , with p∈(1,+∞) and j∈Ξ _ε , there exists an extension $\tilde u \in W^{1,p}(Y_{x_{j}^{\varepsilon }})$ from $Y^{\ast }_{x_{j}^{\varepsilon }, K}$ into $Y_{x_{j}^{\varepsilon }}$ such that

$$ \|\tilde u\|_{L^{p}(Y_{x_{j}^{\varepsilon}})} \leq \mu \|u\|_{L^{p}(Y_{x_{j}^{\varepsilon},K}^{\ast})}, \qquad \|\nabla \tilde u\|_{L^{p}(Y_{x_{j}^{\varepsilon}})} \leq \mu \|\nabla u\|_{L^{p}(Y_{x_{j}^{\varepsilon},K}^{\ast})}, $$

(7)

where μ depends on Y ₁ , Y ₀ , R and K and is independent of ε and j∈Ξ _ε .

For $u \in W^{1,p}({\Omega }^{\ast }_{\varepsilon })$ we have an extension $\tilde u \in W^{1,p}({\Omega })$ from ${\Omega }_{\varepsilon }^{\ast }$ into Ω such that

$$ \|\tilde u\|_{L^{p}({\Omega})} \leq \mu \|u\|_{L^{p}({\Omega}^{\ast}_{\varepsilon})}, \qquad \|\nabla \tilde u\|_{L^{p}({\Omega})} \leq \mu \|\nabla u\|_{L^{p}({\Omega}^{\ast}_{\varepsilon})}, $$

(8)

where μ depends on Y ₁ , Y ₀ , R and K and is independent of ε.

Proof

(Sketch) The proof follows the same lines as in the periodic case, see e.g. [15, 19]. The only difference here is that the extension depends on the Lipschitz continuity of K and R and the uniform boundedness from above and below of |detK(x)| and |detR(x)| for all $x\in \overline {\Omega }$.

To show (8), we first consider the extension from $R_{x_{j}^{\varepsilon }}((Y_{1} \setminus K_{x_{j}^{\varepsilon }} Y_{0}) + j)$ into $R_{x_{j}^{\varepsilon }}(Y_{1}+j)$ and obtain the estimates in (7). Notice that due to the definition of K(x), the fibre radius varies between different fibres in the plywood-like structure of the heart tissue, but is constant along each individual fibre. Thus, apart from the end parts of the fibres near ∂Ω, we have to extend u only in the directions orthogonal to the fibres. In the definition of ${\Omega }_{\varepsilon }^{\ast }$ we consider those j that $\varepsilon R_{x_{j}^{\varepsilon }}(\overline Y_{1}+j)\subset {\Omega }$. Hence the extension for the end parts of the fibres near ∂Ω, i.e., for such $R_{x_{j}^{\varepsilon }}((Y_{1} \setminus K_{x_{j}^{\varepsilon }} Y_{0}) + j)$ that $\bigcup _{m \in \{0,1\}^{3}} \varepsilon R_{x_{j}^{\varepsilon }}(\overline Y_{1} + j \pm m)\cap \partial {\Omega } \ne \emptyset$, is also well-defined. Since detR(x)=1, and $0<{\rho _{0}^{2}}\leq |\det K(x)|\leq {\rho _{1}^{2}}< \infty$ for all $x\in \overline {\Omega }$, we obtain that the constant μ in (7) is independent of $x_{j}^{\varepsilon }$, ε, and j∈Ξ _ε . Then scaling $R_{x_{j}^{\varepsilon }}((Y_{1} \setminus K_{x_{j}^{\varepsilon }} Y_{0}) + j)$ and $R_{x_{j}^{\varepsilon }}(Y_{1}+j)$ by ε and summing up over j∈Ξ _ε in (7) imply (8).

In the case when the boundary ∂Ω crosses the fibres in a non-orthogonal way, we would obtain only a local extension to a subdomain Ω^δ={x∈Ω:dist(x,∂Ω)>δ} for any fixed δ>0. □

4 Derivation of Macroscopic Equations

To derive macroscopic equations for the microscopic problem posed in a domain with the non-periodic plywood-like microstructure, we approximate it by a problem defined in the domain with the corresponding locally periodic microstructure and apply the methods of locally periodic two-scale convergence (l-t-s) and l-p unfolding operator (see Appendix for the definitions and convergence results for l-t-s convergence and l-p unfolding operator). Notice that the regularity assumptions on the orientation angle γ are essential for the construction of an appropriate locally periodic microstructure for the non-periodic plywood-like structure.

To define the locally periodic microstructure related to the original non-periodic one, we consider, similarly to [8, 29], the partition covering of Ω by a family of open non-intersecting cubes $\{{\Omega }_{n}^{\varepsilon }\}_{1\leq n\leq N_{\varepsilon }}$ of side ε ^r, with 0<r<1, such that

$${\Omega}\subset \bigcup\limits_{n=1}^{N_{\varepsilon}} \overline{\Omega}_{n}^{\varepsilon} \qquad \text{and} \qquad {\Omega}_{n}^{\varepsilon} \cap {\Omega} \neq \emptyset. $$

For each $x \in \mathbb R^{3}$, we consider a transformation matrix $D(x)\in \mathbb R^{3\times 3}$ and assume that $D, D^{-1} \in \text {Lip}(\mathbb R^{3}; \mathbb R^{3\times 3})$ and 0<d ₀≤|detD(x)|≤d ₁<∞ for all $x\in \overline {\Omega }$. The matrix D will be defined by the rotation matrix R and its derivatives and the specific form of D will be given later.

Then, the locally periodic microstructure is defined by considering a covering of ${\Omega }_{n}^{\varepsilon }$ by parallelepipeds $\varepsilon D_{x_{n}^{\varepsilon }}Y$ such that

$${\Omega}_{n}^{\varepsilon} \subset \tilde x_{n}^{\varepsilon} + \bigcup_{\xi \in {\Xi}_{n}^{\varepsilon}} \varepsilon D_{x_{n}^{\varepsilon}}(\overline Y+ \xi), \quad \text{ where}\,\,\, {\Xi}_{n}^{\varepsilon}= \{\xi \in \mathbb Z^{3}: \varepsilon D_{x_{n}^{\varepsilon}}(Y+ \xi) \cap {\Omega}_{n}^{\varepsilon} \neq \emptyset\}, $$

and points $x_{n}^{\varepsilon }, \tilde x_{n}^{\varepsilon } \in {\Omega }_{n}^{\varepsilon }$, for n=1,…,N _ε , are arbitrary chosen, but fixed. Here Y=(0,1)³, D _x : = D(x), and $D_{x_{n}^{\varepsilon }} = D(x_{n}^{\varepsilon })$ for 1≤n≤N _ε . Then, the perforated domain with locally periodic microstructure is given by

$$\widetilde {\Omega}^{\ast}_{\varepsilon} = \text{Int}\left(\bigcup\limits_{n=1}^{N_{\varepsilon}} {\Omega}_{n}^{\ast, \varepsilon}\right) \cap {\Omega}, \quad \text{ with} \,\,\,{\Omega}_{n}^{\ast, \varepsilon}= \left(\tilde x_{n}^{\varepsilon} + \bigcup\limits_{\xi \in {\Xi}_{n}^{\varepsilon}}\varepsilon D_{x_{n}^{\varepsilon}}(\overline Y_{K_{x_{n}^{\varepsilon}}}^{\ast} + \xi) \right)\cap \overline {\Omega}_{n}^ \varepsilon, $$

where $Y_{K_{x_{n}^{\varepsilon }}}^{\ast } = Y \setminus \bigcup _{j \in \{0,1\}^{3}}(\widetilde K_{x_{n}^{\varepsilon }} Y_{0}+ j)$, with $\widetilde K_{x_{n}^{\varepsilon }} = \widetilde K(x_{n}^{\varepsilon })$ for n=1,…,N _ε , and the transformation matrix $\widetilde K$ will be specified later. We shall also denote

$$\hat {\Omega}_{n}^{\varepsilon} = \tilde x_{n}^{\varepsilon}+\text{Int} \left(\bigcup\limits_{\xi \in \hat {\Xi}_{n}^{\varepsilon}} \varepsilon D_{x_{n}^{\varepsilon}}(\overline{Y}+ \xi)\right) \quad \text{ and} \quad {\Lambda}_{\varepsilon}^{\ast} = \widetilde {\Omega}_{\varepsilon}^{\ast} \setminus \bigcup\limits_{n=1}^{N_{\varepsilon}} \hat {\Omega}_{n}^{\varepsilon}, $$

where $\hat {\Xi }^{\varepsilon }_{n} =\{\xi \in {\Xi }_{n}^{\varepsilon } : \varepsilon D_{x_{n}^{\varepsilon }}(Y+ \xi ) \subset ({\Omega }_{n}^{\varepsilon } \cap {\Omega })\}$. The boundaries of the locally periodic microstructure are defined as

$$\widetilde {\Gamma}^{\varepsilon} =\bigcup\limits_{n=1}^{N_{\varepsilon}} {\Gamma}_{n}^{\varepsilon}\cap {\Omega}, \quad \text{ where}\,\,\, {\Gamma}_{n}^{\varepsilon}= \left(\tilde x_{n}^{\varepsilon} + \bigcup_{\xi\in {\Xi}_{n}^{\varepsilon}} \varepsilon D_{x_{n}^{\varepsilon}} (\widetilde {\Gamma}_{x_{n}^{\varepsilon},K} + \xi)\right)\cap {\Omega}_{n}^{\varepsilon}, $$

and

$$\hat {\Gamma}^{\varepsilon} = \bigcup\limits_{n=1}^{N_{\varepsilon}}\left(\tilde x_{n}^{\varepsilon} + \bigcup\limits_{\xi\in \hat {\Xi}_{n}^{\varepsilon}} \varepsilon D_{x_{n}^{\varepsilon}} (\widetilde {\Gamma}_{x_{n}^{\varepsilon},K} + \xi)\right), $$

where $\widetilde {\Gamma }_{x_{n}^{\varepsilon },K}= \widetilde K_{x_{n}^{\varepsilon }} {\Gamma }$ and ${\Gamma }= \overline {\partial Y_{0}\setminus {\Gamma }_{0,1}}$. For the problem analyzed here, we shall consider $\tilde x_{n}^{\varepsilon } = x_{n}^{\varepsilon }$.

The following calculations illustrate the motivation for the locally periodic approximation and determine formulas for the transformation matrices D and $\widetilde K$. For n=1,…,N _ε , we choose such $\kappa _{n} \in \mathbb Z^{3}$ that for $x_{n}^{\varepsilon }=R_{x_{n}^{\varepsilon }}\varepsilon \kappa _{n}$ we have $x_{n}^{\varepsilon } \in {\Omega }_{n}^{\varepsilon }$. In the definition of covering of ${\Omega }_{n}^{\varepsilon }$ by shifted parallelepipeds, we consider a numbering of $\xi \in {\Xi }_{n}^{\varepsilon }$ and write

$${\Omega}_{n}^{\varepsilon}\subset x_{n}^{\varepsilon} + \bigcup\limits_{j=1}^{I_{n}^{\varepsilon}} \varepsilon D_{x_{n}^{\varepsilon}}(\overline Y+\xi_{j}) \quad \qquad \text{ for} \,\,\, \xi_{j}\in {\Xi}_{n}^{\varepsilon}. $$

Then for $1\leq j \leq I_{n}^{\varepsilon }$ we consider ${k_{j}^{n}} = \kappa _{n} + \xi _{j}$ and $x_{{k_{j}^{n}}}^{\varepsilon }= R_{{k_{j}^{n}}}\varepsilon {k_{j}^{n}}$. Here $R_{{k_{j}^{n}}}:=R_{x_{{k_{j}^{n}}}^{\varepsilon }}$ and $R_{\kappa _{n}} := R_{x_{n}^{\varepsilon }}$.

Using the regularity assumptions on the function γ and considering the Taylor expansion of R ⁻¹ around $x_{n}^{\varepsilon }$, i.e. around ε κ _n,3, we obtain

$$\begin{array}{@{}rcl@{}} &&R^{-1}_{{k_{j}^{n}}}(x- x_{{k_{j}^{n}}}^{\varepsilon}) = R^{-1}_{{k_{j}^{n}}} x- \varepsilon {k_{j}^{n}}\\ && = R^{-1}_{\kappa_{n}}x + (R_{\kappa_{n}}^{-1})^{\prime} x_{n}^{\varepsilon} \xi_{j,3}\varepsilon +(R_{\kappa_{n}}^{-1})^{\prime}(x- x_{n}^{\varepsilon}) \xi_{j,3}\varepsilon + b(|\xi_{j,3} \varepsilon|^{2})x - \varepsilon(\kappa_{n}+ \xi_{j}) \\ && = R_{\kappa_{n}}^{-1}(x -x_{n}^{\varepsilon})- \widetilde W_{x_{n}^{\varepsilon}}\xi_{j}\varepsilon +(R_{\kappa_{n}}^{-1})^{\prime}(x- x_{n}^{\varepsilon}) \xi_{j,3}\varepsilon+ b(|\xi_{j,3} \varepsilon|^{2})x, \end{array} $$

(9)

where $\widetilde W_{x_{n}^{\varepsilon }} = \widetilde W(x_{n}^{\varepsilon })$ with $\widetilde W(x)=(I- \nabla R^{-1}(\gamma (x_{3})) x)$. The notation of the gradient is understood as ∇R ⁻¹(γ(x))x=∇ _z (R ⁻¹(γ(z))x)| _{z = x} . Thus, for $x, x_{n}^{\varepsilon }\in {\Omega }_{n}^{\varepsilon }$, since $|x- x_{n}^{\varepsilon }| \leq C\varepsilon ^{r}$, the distance between $R^{-1}_{x^{\varepsilon }_{n}} (x -x_{n}^{\varepsilon })- \widetilde W_{x_{n}^{\varepsilon }} \xi _{j}\varepsilon$ and $R^{-1}_{{k_{j}^{n}}}(x- x_{{k_{j}^{n}}}^{\varepsilon })$ is of the order $\sup _{1\leq j\leq I_{n}^{\varepsilon }} |\xi _{j}\varepsilon |^{2} \sim \varepsilon ^{2r}$.

This calculation together with the estimates below will ensure that the non-periodic plywood-like structure can be approximated by the corresponding locally periodic microstructure, comprising $\widetilde Y_{x_{n}^{\varepsilon }}$-periodic structure in each ${\Omega }_{n}^{\varepsilon }$ for n=1,…,N _ε , and $|{\Omega }_{n}^{\varepsilon }|\sim \varepsilon ^{3r}$ for an appropriate r∈(0,1). Here $\widetilde Y_{x}= D(x)Y$, with D(x) = R _x W(x), and

$$ W(x) = \left(\begin{array}{cccc} 1 \;& 0 & 0\\ 0&1\; & w(x)\\ 0&0&1 \end{array}\right), $$

(10)

where w(x) = γ ^′(x ₃)(cos(γ(x ₃))x ₁+ sin(γ(x ₃))x ₂) and R _x = R(γ(x ₃)). The transformation matrix $\widetilde K$ is defined as $\widetilde K(x) = W^{-1}(x) K(x)$ and the boundary of the muscle fibres in the locally periodic approximation is given by $\widetilde {\Gamma }_{x}= D(x) \widetilde K(x) {\Gamma }= R_{x} K(x) {\Gamma }$.

The definitions of R, W and γ ensure that the transformation matrices D and $\widetilde K$ are Lipschitz continuous, as well as 0<d ₀≤|detD(x)|≤d ₁<∞ and $0 < {\rho _{0}^{2}} \leq |\det \widetilde K(x) | \leq {\rho _{1}^{2}} <\infty$ for all $x\in \overline {\Omega }$. Since 𝜗 is independent of the first variable, we consider in the definition of W(x) the shift only in the second variable. Notice that if the original microstructure would be locally periodic, i.e. $R(\gamma (x_{3})) = R(\gamma (x_{n,3}^{\varepsilon }))$ for $x\in {\Omega }_{n}^{\varepsilon }$ and some $x_{n}^{\varepsilon } \in {\Omega }_{n}^{\varepsilon }$, then the matrix W would be constant in each ${\Omega }_{n}^{\varepsilon }$ and we would obtain D(x) = R(γ(x ₃)) for x∈Ω.

In the approximation of the problem posed in the domain with the non-periodic plywood-like structure, we shall use the following lemma, proven in [6], that facilitate the estimate for the difference between the values of the characteristic function at two different points.

Lemma 3 (6)

Let χ _b be the characteristic function of the fibre of radius b, i.e., χ _b (x)=1 for $|\hat x|\leq b$ and χ _b (x)=0 for $|\hat x|>b$ , with $\hat x = (x_{2}, x_{3})$ . Then

$$\|\chi_{b}(x+\delta) - \chi_{b}(x)\|^{2}_{L^{2}({\Omega})} \leq C b L |\delta| \quad\text{ for all}\,\, b>0 \, \text{ and}\,\, |\delta|\leq b, $$

where L is the length of the fibre and the constant C is independent of b, δ, and L.

Deriving estimates for the difference of solutions of the original microscopic problem and the corresponding locally periodic approximation and applying techniques of locally periodic homogenization, we obtain the following macroscopic equations for the microscopic problem (1) and (2).

Theorem 1

A sequence of solutions of the microscopic problem (1) and (2) converges to a solution

$$c \in L^{2}(0,T; H^{1}({\Omega})) \cap H^{1}(0,T; L^{2}({\Omega})) \quad \text{ and} \quad r_{l} \in H^{1}(0,T; L^{2}({\Omega}; L^{2}(\widetilde{\Gamma}_{x}))), $$

where l=f,b, of the macroscopic equations

$$\begin{array}{@{}rcl@{}} \theta(x) \partial_{t} c - \text{div} (\mathcal A(x) \nabla c) &=& \theta(x) F(c) +\frac 1 {|\widetilde Y_{x}|} {\int}_{\widetilde {\Gamma}_{x}}\left[\widetilde \beta(x,y) r_{b} -\widetilde \alpha(x,y) r_{f} c \right] d\sigma_{y}, \\ \mathcal A(x) \nabla c \cdot \textbf{n} &=&0 \qquad \text{ on} \,\,\, \partial{\Omega}\times (0,T), \\ \partial_{t} r_{f} &=& p(r_{b}) - \widetilde \alpha(x,y) r_{f} \, c + \widetilde \beta(x, y) r_{b} - d_{f}\, r_{f}, \\ \partial_{t} r_{b}&=& \widetilde \alpha(x,y) r_{f} \, c - \widetilde \beta(x,y)r_{b} - d_{b} \, r_{b}, \end{array} $$

(11)

for (t,x)∈(0,T)×Ω and $y \in \widetilde {\Gamma }_{x}$ , where the macroscopic diffusion coefficient $\mathcal A$ is defined as

$$\mathcal A_{ij}(x) = \frac 1{|\widetilde Y_{x}|}{\int}_{\widetilde Y^{\ast}_{x,K}} (A_{ij} + A_{ik} \partial_{y_{k}} w^{j}(x,y) ) dy, $$

with w ^j , for j=1,2,3, which are solutions of the unit cell problems

$$ \begin{array}{rll} \text{div} (A(\nabla_{y} w^{j} + \textbf{e}_{j})) &= 0 \quad & \text{ in}\,\, \widetilde Y^{\ast}_{x,K},\\ A(\nabla_{y} w^{j} + \textbf{e}_{j})\cdot \textbf{n} &=0 \quad & \text{ on}\,\, \widetilde {\Gamma}_{x}, \quad w^{j} \; \; \widetilde Y_{x}-\text{periodic},{\int}_{\widetilde{Y}_{x}^{\ast}w^{j}d_{y}=\,0}. \end{array} $$

(12)

Here

$$\begin{array}{@{}rcl@{}} \widetilde Y_{x,K}^{\ast}&=& D_{x}\left(Y \setminus \bigcup\limits_{m \in \{ 0,1\}^{3}} (\widetilde K_{x} Y_{0}+ m)\right),\qquad \widetilde Y_{x}= D_{x} Y,\\ \widetilde {\Gamma}_{x} &=& \bigcup\limits_{m\in \{0,1\}^{3}} D_{x}(\widetilde K_{x}{\Gamma}+ m) \cap \widetilde Y_{x}, \qquad \theta(x) = \frac{|\widetilde Y^{\ast}_{x,K}|}{|\widetilde Y_{x}|}, \end{array} $$

where Y=(0,1) ³ , R _x =R(γ(x ₃ )), D _x =R _x W _x , $\widetilde K_{x} = W_{x}^{-1} K_{x}$ , with W _x =W(x) defined by (10), and

$$\begin{array}{@{}rcl@{}} \widetilde \alpha(x,y)&=& \sum\limits_{m\in \mathbb Z^{3}} \alpha(x, R^{-1}_{x}(y - D_{x} m)), \\ \widetilde \beta(x,y)&=& \sum\limits_{m\in \mathbb Z^{3}} \beta(x, R^{-1}_{x}(y - D_{x} m)). \end{array} $$

(13)

Proof

Using calculations from above, we consider a domain with a locally periodic microstructure characterised by the periodicity cell $\widetilde Y_{x_{n}^{\varepsilon }} = D_{x_{n}^{\varepsilon }} Y$ in each ${\Omega }_{n}^{\varepsilon }$, with n=1,…,N _ε and the shift $x_{n}^{\varepsilon } \in {\Omega }_{n}^{\varepsilon }$ in the covering of ${\Omega }_{n}^{\varepsilon }$ by $D_{x_{n}^{\varepsilon }} (Y+\xi )$, with $\xi \in {\Xi }_{n}^{\varepsilon }$.

Then, the characteristic function of the extracellular space $\widetilde {\Omega }^{\ast }_{\varepsilon }$ in a tissue with locally periodic microstructure is defined by $\chi _{\widetilde {\Omega }^{\ast }_{\varepsilon }}= (1- \chi _{\widetilde {\Omega }^{\varepsilon }_{f}})\chi _{\Omega }$, where $\chi _{\widetilde {\Omega }^{\varepsilon }_{f}}$ denotes the characteristic function of fibres

$$\chi_{\widetilde {\Omega}^{\varepsilon}_{f}} = {\sum}_{n=1}^{N_{\varepsilon}} \chi_{\widetilde {\Omega}^{\varepsilon}_{n,f}} \quad \text{ and} \quad \chi_{\widetilde {\Omega}^{\varepsilon}_{n,f}} = {\sum}_{\xi\in {\Xi}_{n}^{\varepsilon}} \vartheta(x_{n}^{\varepsilon}, R^{-1}_{x_{n}^{\varepsilon}}(x- x_{n}^{\varepsilon}- \varepsilon D_{x_{n}^{\varepsilon}} \xi)/\varepsilon) \chi_{{\Omega}_{n}^{\varepsilon}}. $$

The boundaries of the locally periodic microstructure are denoted by

$$\widetilde {\Gamma}^{\varepsilon} = \bigcup\limits_{n=1}^{N_{\varepsilon}}\bigcup\limits_{\xi\in {\Xi}_{n}^{\varepsilon}} (x_{n}^{\varepsilon} + \varepsilon R_{x_{n}^{\varepsilon}} K_{x_{n}^{\varepsilon}} {\Gamma} + \varepsilon D_{x_{n}^{\varepsilon}} \xi)\cap{\Omega}. $$

Notice that non-periodic changes in the shape of the perforations (radius of muscle fibres) are approximated by the same transformation matrix K(x). This is consistent with the results obtained in [10, 11, 23, 33]. However spatial changes in the periodicity are approximated by D _x = R _x W _x .

The reaction rates (binding and dissociation rates) are defined in terms of locally periodic microstructure in the following way

$$\begin{array}{@{}rcl@{}} \widetilde \alpha^{\varepsilon}(x)&=& \sum\limits_{n=1}^{N_{\varepsilon}}\sum\limits_{\xi \in {\Xi}_{n}^{\varepsilon}} \alpha(x,(R^{-1}_{x_{n}^{\varepsilon}}(x-x_{n}^{\varepsilon}) - W_{x_{n}^{\varepsilon}} \varepsilon \xi)/\varepsilon)\chi_{{\Omega}_{n}^{\varepsilon}},\\ \widetilde \beta^{\varepsilon}(x)&=& \sum\limits_{n=1}^{N_{\varepsilon}}\sum\limits_{\xi \in {\Xi}_{n}^{\varepsilon}}\beta(x,(R^{-1}_{x_{n}^{\varepsilon}}(x-x_{n}^{\varepsilon}) - W_{x_{n}^{\varepsilon}} \varepsilon \xi)/\varepsilon)\chi_{{\Omega}_{n}^{\varepsilon}}. \end{array} $$

To show that we can approximate the problem (1) and (2) by a microscopic problem defined in the domain with the locally periodic microstructure, we have to prove that the difference between the characteristic function of the original domain $\chi _{{\Omega }^{\ast }_{\varepsilon }}$ and of the locally periodic perforated domain $\chi _{\widetilde {\Omega }^{\ast }_{\varepsilon }}$ converges to zero strongly in L ²(Ω) as ε→0. Also, we have to show that the difference between boundary integrals and their locally periodic approximations converges to zero as ε→0. This will ensure that as ε→0 the sequence of solutions of the original microscopic problem (1)–(2) will converge to a solution of the macroscopic equations obtained by homogenization of the corresponding problem defined in the domain with locally periodic microstructure.

For the difference between $\chi _{{\Omega }_{\varepsilon }^{\ast }}$ and $\chi _{\widetilde {\Omega }_{\varepsilon }^{\ast }}$, we have

$$\begin{array}{@{}rcl@{}} && {\int}_{\Omega} |\chi_{{\Omega}_{\varepsilon}^{\ast}} - \chi_{\widetilde {\Omega}_{\varepsilon}^{\ast}}|^{2} dx \leq \mathcal I_{1} +\mathcal I_{2}\\ &&= \sum\limits_{n=1}^{N_{\varepsilon}} {\int}_{{\Omega}_{n}^{\varepsilon}} \sum\limits_{j \in J_{n}^{\varepsilon}} \left|\vartheta(x^{\varepsilon}_{k_{j}}, R^{-1}_{x_{k_{j}}^{\varepsilon}}(x-x_{k_{j}}^{\varepsilon})/\varepsilon) - \vartheta(x_{n}^{\varepsilon}, R^{-1}_{x_{k_{j}}^{\varepsilon}}(x-x^{\varepsilon}_{k_{j}})/\varepsilon)\right|^{2} dx \\ &&\quad +\sum\limits_{n=1}^{N_{\varepsilon}} {\int}_{{\Omega}_{n}^{\varepsilon}} \sum\limits_{j \in J_{n}^{\varepsilon}} \left|\vartheta(x_{n}^{\varepsilon}, R^{-1}_{x_{k_{j}}^{\varepsilon}}(x-x_{k_{j}}^{\varepsilon})/\varepsilon) - \vartheta(x^{\varepsilon}_{n}, (R^{-1}_{x_{n}^{\varepsilon}}(x- x_{n}^{\varepsilon}) - \varepsilon W_{x_{n}^{\varepsilon}} j)/\varepsilon)\right|^{2} dx, \end{array} $$

where $x^{\varepsilon }_{n}=R_{x^{\varepsilon }_{n}} \varepsilon \kappa _{n}$, $x^{\varepsilon }_{k_{j}}= R_{x^{\varepsilon }_{k_{j}}} \varepsilon k_{j}$, with k _j = κ _n + j, and

$$J_{n}^{\varepsilon}=\left\{j \in \mathbb Z^{3}: \left[\left(x^{\varepsilon}_{k_{j}}+\varepsilon R_{x^{\varepsilon}_{k_{j}}}Y_{1}\right) \cup \left(x^{\varepsilon}_{n} + \varepsilon R_{x^{\varepsilon}_{n}} Y_{1} + \varepsilon D_{x_{n}^{\varepsilon}} j\right) \right]\cap {\Omega}_{n}^{\varepsilon} \neq \emptyset \right\}. $$

We notice that $\varepsilon ^{3} |J_{n}^{\varepsilon }| \leq C \varepsilon ^{3r}$ and |N _ε |≤C ε ^−3r. For the first integral, we have

$$\mathcal I_{1} \leq \sum\limits_{n=1}^{N_{\varepsilon}}\varepsilon^{3} |J_{n}^{\varepsilon}| \|\nabla \rho\|_{L^{\infty}({\Omega})} \sup_{j \in J_{n}^{\varepsilon}}|x_{n}^{\varepsilon} - x^{\varepsilon}_{k_{j}}| \leq C \varepsilon^{r}. $$

To estimate the second integral, we use Lemma 3. Since in each ${\Omega }_{n}^{\varepsilon }$ the length of fibres is of order ε ^r, applying estimate in Lemma 3, equality (9), and the estimates N _ε ≤C ε ^−3r and $|J_{n}^{\varepsilon }|\leq C \varepsilon ^{3(r-1)}$, we conclude that

$$ \mathcal I_{2} \leq C\varepsilon^{3r-2}. $$

Thus, for r∈(2/3,1), we have $\mathcal I_{1}\to 0$ and $\mathcal I_{2} \to 0$ as ε→0.

To estimate the difference between boundary integral we have to extend c ^ε, $r_{f}^{\varepsilon }$, and $r_{b}^{\varepsilon }$ from ${\Omega }_{\varepsilon }^{\ast }$ to Ω. For c ^ε, we can consider the extension as in Lemma 2. Then, using the extended $\tilde c^{\varepsilon }$ and the fact that the reaction rates and the initial data are defined on whole Ω we can extend $r_{f}^{\varepsilon }$ and $r_{b}^{\varepsilon }$ to Ω as solutions of the ordinary differential equations with $\tilde c^{\varepsilon }$ instead of c ^ε

$$ \begin{array}{rll} \partial_{t} \tilde r^{\varepsilon}_{f} &= p(\tilde r_{b}^{\varepsilon}) - \alpha^{\varepsilon}(x)\, \tilde c^{\varepsilon}\, \tilde r_{f}^{\varepsilon} + \beta^{\varepsilon}(x) \, \tilde r_{b}^{\varepsilon} -d_{f}\, \tilde r_{f}^{\varepsilon} \quad & \text{ in}\,\,\, (0,T)\times {\Omega},\\ \partial_{t} \tilde r^{\varepsilon}_{b} &= \alpha^{\varepsilon}(x)\, \tilde c^{\varepsilon} \, \tilde r_{f}^{\varepsilon} - \beta^{\varepsilon}(x)\, \tilde r_{b}^{\varepsilon} - d_{b}\, \tilde r_{b}^{\varepsilon} \quad & \text{ on} \,\,\, (0,T)\times {\Omega}, \\ \tilde r_{f}^{\varepsilon}(0, x) &= r_{f0}^{\varepsilon}(x), \qquad \tilde r_{b}^{\varepsilon}(0, x) = r_{b0}^{\varepsilon}(x) \quad & \text{ in} \,\,\, {\Omega}. \end{array} $$

(14)

The non-negativity of c ^ε and the construction of the extension ensure that $\tilde c^{\varepsilon }$ is non-negative. Then, in the same way as for $r_{f}^{\varepsilon }$ and $r_{b}^{\varepsilon }$, using the properties of p and the non-negativity of the coefficients and initial data, we obtain the non-negativity of $\tilde r^{\varepsilon }_{f}$ and $\tilde r_{b}^{\varepsilon }$. Thus, adding the equations for $\tilde r^{\varepsilon }_{f}$ and $\tilde r^{\varepsilon }_{b}$, we obtain the boundedness of $\tilde r^{\varepsilon }_{f}$ and $\tilde r^{\varepsilon }_{b}$ in Ω _T , i.e.

$$\|\tilde r^{\varepsilon}_{f}\|_{L^{\infty}({\Omega}_{T})} + \|\tilde r^{\varepsilon}_{b}\|_{L^{\infty}({\Omega}_{T})} \leq C. $$

Differentiating equations in (14) with respect to x and using the estimate $\|\nabla \tilde r_{b}^{\varepsilon }\|_{L^{2}({\Omega })} \leq \|\nabla \tilde r_{b}^{\varepsilon }+\nabla \tilde r_{f}^{\varepsilon } \|_{L^{2}({\Omega })} + \|\nabla \tilde r_{f}^{\varepsilon } \|_{L^{2}({\Omega })}$, we obtain

$$\begin{array}{@{}rcl@{}} && \|\nabla \tilde r^{\varepsilon}_{f}\|_{L^{\infty}(0,T; L^{2}({\Omega}))} + \|\nabla \tilde r^{\varepsilon}_{b}\|_{L^{\infty}(0,T; L^{2}({\Omega}))} \leq \mu_{1} \| \nabla \tilde c^{\varepsilon}\|_{L^{2}({\Omega}_{T})} \\ &&+ \varepsilon^{-1} \mu_{2} \|\tilde c^{\varepsilon}\|_{L^{2}({\Omega}_{T})} + \varepsilon^{-1}\mu_{3}\left[ \| \tilde r_{f}^{\varepsilon}\|_{L^{\infty}({\Omega}_{T})} + \|\tilde r_{b}^{\varepsilon}\|_{L^{\infty}({\Omega}_{T})} \right]\leq \mu_{4} \left(1 + \frac 1\varepsilon\right), \end{array} $$

(15)

where the constants μ _j , with j=2,3,4, depend on the derivatives of α, β, and μ _j , with j=1,2,3,4, are independent of ε. Hence, for each ε>0, the extensions $\tilde r^{\varepsilon }_{f}$, $\tilde r_{b}^{\varepsilon }$, and $\tilde c^{\varepsilon }$ are well-defined on the boundaries $\widetilde {\Gamma }^{\varepsilon }$ of the locally periodic microstructure. In what follows we shall use the same notation for a function and for its extension.

Notice that ε ⁻¹ in the estimates for $\nabla r^{\varepsilon }_{f}$ and $\nabla r^{\varepsilon }_{b}$ will be compensated by ε in the estimate for the difference between neighbouring points in non-periodic and locally periodic domains, respectively, i.e.

$$|\varepsilon R_{x^{\varepsilon}_{k_{j}}} K_{x_{k_{j}}^{\varepsilon}} y - \varepsilon R_{x_{n}^{\varepsilon}}K_{x_{n}^{\varepsilon}} y| \leq C \varepsilon^{1+r}(1+\|\gamma^{\prime}\|_{L^{\infty}(\mathbb R)})(1+ \|\nabla K \|_{L^{\infty}({\Omega})}). $$

Then, for the boundary integrals, we have

$$\begin{array}{@{}rcl@{}} &&\varepsilon \left|{\int}_{{\Gamma}^{\varepsilon}} \alpha^{\varepsilon} r^{\varepsilon}_{f} c^{\varepsilon}\psi d\sigma_{x}^{\varepsilon} - {\int}_{\widetilde {\Gamma}^{\varepsilon}}\widetilde \alpha^{\varepsilon} r^{\varepsilon}_{f} c^{\varepsilon} \psi d\sigma_{x}^{\varepsilon}\right| \leq \mathcal I_{3} + \mathcal I_{4}\\ && = \varepsilon \sum\limits_{n=1}^{N_{\varepsilon}} \sum\limits_{j \in J_{n}^{\varepsilon}}\left| {\int}_{\varepsilon K^{R}_{x_{k_{j}}^{\varepsilon}}{\Gamma} + x_{k_{j}}^{\varepsilon}} \alpha^{\varepsilon} r^{\varepsilon}_{f} c^{\varepsilon} \psi d\sigma_{x}^{\varepsilon} - {\int}_{\varepsilon K^{R}_{x_{n}^{\varepsilon}}{\Gamma} + x_{k_{j}}^{\varepsilon}} \alpha^{\varepsilon} r^{\varepsilon}_{f} c^{\varepsilon}\psi d\sigma_{x}^{\varepsilon}\right| \\ &&\quad +\varepsilon \sum\limits_{n=1}^{N_{\varepsilon}} \sum\limits_{j \in J_{n}^{\varepsilon}}\left| {\int}_{\varepsilon K^{R}_{x_{n}^{\varepsilon}}{\Gamma} + x_{k_{j}}^{\varepsilon}} \alpha^{\varepsilon} r^{\varepsilon}_{f} c^{\varepsilon} \psi d\sigma_{x}^{\varepsilon} - {\int}_{\varepsilon K^{R}_{x_{n}^{\varepsilon}}{\Gamma} + x_{n}^{\varepsilon} + \varepsilon D_{x_{n}^{\varepsilon}} j}\widetilde \alpha^{\varepsilon} r^{\varepsilon}_{f} c^{\varepsilon} \psi d\sigma_{x}^{\varepsilon}\right| \end{array} $$

for $\psi \in C^{1}(\overline {\Omega }_{T})$, where ${K^{R}_{x}}= R_{x} K_{x}$. Considering the regularity of K and R and the uniform boundedness from below and above of |detK|, and using the trace estimate for the L ²(Γ)-norm of a H ^σ(Y)-function, with σ∈(1/2,1), the first integral we can estimates as

$$\begin{array}{@{}rcl@{}} \mathcal I_{3} &\leq& C_{1} \varepsilon^{d} \sum\limits_{n=1}^{N_{\varepsilon}} \sum\limits_{j \in J_{n}^{\varepsilon}} {\int}_{\Gamma} \left|\alpha^{\varepsilon} r^{\varepsilon}_{f} (t,y_{k_{j}^{\varepsilon}}) c^{\varepsilon}(t,y_{k_{j}^{\varepsilon}}) - \alpha^{\varepsilon} r^{\varepsilon}_{f} (t,y_{\kappa_{n}^{\varepsilon}}) c^{\varepsilon}(t,y_{\kappa_{n}^{\varepsilon}})\right| d\sigma_{y}+ C_{2} \varepsilon^{r}\\ & \leq& C_{3}\left[\varepsilon^{\frac{d+1}2} \sum\limits_{n=1}^{N_{\varepsilon}} \sum\limits_{j \in J_{n}^{\varepsilon}} \|c^{\varepsilon}\|_{L^{2}({\Gamma}_{n,j}^{\varepsilon})}\left[{\int}_{\Gamma} \left|\alpha^{\varepsilon}(y_{k_{j}^{\varepsilon}}) - \alpha^{\varepsilon}(y_{\kappa_{n}^{\varepsilon}})\right|^{2} d\sigma_{y} \right]^{\frac 12} \right]\\ &&\left.+ C_{4} \varepsilon^{d} \sum\limits_{n=1}^{N_{\varepsilon}} \sum\limits_{j \in J_{n}^{\varepsilon}}\left[{\vphantom{\left.+ C_{4} \varepsilon^{d} \sum\limits_{n=1}^{N_{\varepsilon}} \sum\limits_{j \in J_{n}^{\varepsilon}}\left[{\int}_{Y} | c^{\varepsilon}(t,y_{k_{j}^{\varepsilon}}) - c^{\varepsilon}(t,y_{\kappa_{n}^{\varepsilon}})|^{2} + | r^{\varepsilon}_{f}(t, y_{k_{j}^{\varepsilon}}) - r_{f}^{\varepsilon}(t,y_{\kappa_{n}^{\varepsilon}})|^{2} dy\right.\right.}}{\int}_{Y} | c^{\varepsilon}(t,y_{k_{j}^{\varepsilon}}) - c^{\varepsilon}(t,y_{\kappa_{n}^{\varepsilon}})|^{2} + | r^{\varepsilon}_{f}(t, y_{k_{j}^{\varepsilon}}) - r_{f}^{\varepsilon}(t,y_{\kappa_{n}^{\varepsilon}})|^{2} dy\right.\right.\\ &&\left.+ {\int}_{Y}{\int}_{Y} \frac{|[c^{\varepsilon}(t,y^{1}_{k_{j}^{\varepsilon}})- c^{\varepsilon}(t,y^{2}_{k_{j}^{\varepsilon}})]- [c^{\varepsilon}(t,y^{1}_{\kappa^{\varepsilon}_{n}})- c^{\varepsilon}(t,y^{2}_{\kappa^{\varepsilon}_{n}})]|^{2}}{|y^{1}-y^{2}|^{2\sigma+ d}} dy^{1} dy^{2}\right. \\ &&\left.+ {\int}_{Y} {\int}_{Y} \frac{|[r^{\varepsilon}_{f}(y^{1}_{k_{j}^{\varepsilon}})-r^{\varepsilon}_{f}(y^{2}_{k_{j}^{\varepsilon}})] - [r^{\varepsilon}_{f}(y^{1}_{\kappa_{n}^{\varepsilon}})-r^{\varepsilon}_{f}(y^{2}_{\kappa_{n}^{\varepsilon}})]|^{2}}{|y^{1}-y^{2}|^{2\sigma+ d}} dy^{1} dy^{2} \right]^{\frac 12}\\ &&\times \left[{\int}_{\Gamma} \left(|c^{\varepsilon}(y_{k_{j}^{\varepsilon}})|^{2} + |r_{f}^{\varepsilon}(y_{\kappa_{n}^{\varepsilon}})|^{2}\right) d \sigma_{y}\right]^{\frac 12}+ C_{5} \varepsilon^{r}, \end{array} $$

where d= dim(Ω)=3 and ${\Gamma }_{n,j}^{\varepsilon } = x_{k_{j}}^{\varepsilon }+ \varepsilon K^{R}_{x_{k_{j}}^{\varepsilon }} {\Gamma } = x_{k_{j}}^{\varepsilon }+\varepsilon R_{x_{k_{j}}^{\varepsilon }}K(x_{k_{j}}^{\varepsilon }){\Gamma }$, with $j \in J_{n}^{\varepsilon }$ and n=1,…,N _ε . Here, we used the short notations

$$\begin{array}{@{}rcl@{}} y_{k_{j}^{\varepsilon}} &=& x_{k_{j}}^{\varepsilon} + \varepsilon K^{R}_{x_{k_{j}}^{\varepsilon}} y, \qquad y_{\kappa_{n}^{\varepsilon}} =x_{k_{j}}^{\varepsilon}+ \varepsilon K^{R}_{x_{n}^{\varepsilon}} y, \\ y^{l}_{k_{j}^{\varepsilon}} &=& x_{k_{j}}^{\varepsilon} + \varepsilon K^{R}_{x_{k_{j}}^{\varepsilon}} y^{l},\qquad y^{l}_{\kappa_{n}^{\varepsilon}} = x_{k_{j}}^{\varepsilon}+\varepsilon K^{R}_{x_{n}^{\varepsilon}} y^{l}\qquad \text{ for}\,\,\, l=1,2. \end{array} $$

Using the regularity of γ, K, and α, and applying a priori estimates for c ^ε and $r^{\varepsilon }_{f}$, together with (15), we obtain for 0<σ ₁<1/2, with σ + σ ₁=1,

$$\begin{array}{@{}rcl@{}} {{\int}_{0}^{T}} \mathcal I_{3}dt &\leq& \mu_{1} \sum\limits_{n=1}^{N_{\varepsilon}} \sum\limits_{j\in J_{n}^{\varepsilon}} {\varepsilon{\int}_{0}^{T}} \left[\|\nabla r^{\varepsilon}_{f}\|_{L^{2}(Y_{k_{j}}^{\varepsilon})} + \|\nabla c^{\varepsilon}\|_{L^{2}(Y_{k_{j}}^{\varepsilon})}+ \|\nabla \alpha^{\varepsilon}\|_{C(Y_{k_{j}}^{\varepsilon})}\right]dt \\ &&\times \|\gamma^{\prime}\|_{L^{\infty}(\mathbb R)} \|\nabla K\|_{L^{\infty}({\Omega})}\left[\sup_{j \in J_{n}^{\varepsilon}}|x_{k_{j}}^{\varepsilon} - x_{n}^{\varepsilon}| +\sup_{j \in J_{n}^{\varepsilon}}|x_{k_{j}}^{\varepsilon} - x_{n}^{\varepsilon}|^{\sigma_{1}}\right] + \mu_{1} \varepsilon^{r}\\ & \leq& \mu \varepsilon^{\sigma_{1} r}, \end{array} $$

where $Y_{k_{j}}^{\varepsilon }= x_{k_{j}}^{\varepsilon }+\varepsilon R_{x_{k_{j}}^{\varepsilon }} Y_{1}$. Conducting similar calculations as for $\mathcal I_{3}$ and using the fact that $|x_{k_{j}}^{\varepsilon } - x_{n}^{\varepsilon } - D_{x_{n}^{\varepsilon }} \varepsilon j| \leq C_{1} |\varepsilon j|^{2}\leq C_{2} \varepsilon ^{2 r}$ yield

$$\begin{array}{@{}rcl@{}} {{\int}_{0}^{T}}\mathcal I_{4} dt &\leq& \mu_{1} \sum\limits_{n=1}^{N_{\varepsilon}} \sum\limits_{j \in J_{n}^{\varepsilon}}{{\int}_{0}^{T}} \left[\|\nabla r^{\varepsilon}_{f}\|_{L^{2}(\widetilde Y_{n,j}^{\varepsilon})} + \|\nabla c^{\varepsilon}\|_{L^{2}(\widetilde Y_{n,j}^{\varepsilon})}+ \|\nabla \widetilde \alpha^{\varepsilon}\|_{C(\widetilde Y_{n,j}^{\varepsilon})}\right] dt\\ &&\times \left(\varepsilon^{1+r} + \varepsilon^{\sigma} \left|R^{-1}_{x_{k_{j}}^{\varepsilon}}(x-x_{k_{j}}^{\varepsilon}) -R^{-1}_{x_{n}^{\varepsilon}}(x- x_{n}^{\varepsilon}) - W_{x_{n}^{\varepsilon}} \varepsilon j\right|^{\sigma_{1}} \right)\\ &\leq& \mu\left[\varepsilon^{(2r-1)\sigma_{1}}+ \varepsilon^{r}\right], \end{array} $$

where σ + σ ₁=1 and $\widetilde Y_{n,j}^{\varepsilon }=x_{n}^{\varepsilon } + \varepsilon R_{x_{n}^{\varepsilon }}Y_{1} + \varepsilon D_{x_{n}^{\varepsilon }} j$. In a similar way, we obtain the estimates for the difference of the other two boundary integrals. Thus, we conclude that for r∈(1/2,1), the difference between the boundary integrals for non-periodic and locally periodic microstructures converges to zero as ε→0.

Notice that since the extensions of c ^ε and $r^{\varepsilon }_{l}$, with l = f,b, are in L ²(0,T;H ¹(Ω)) and ∂Ω is Lipschitz continuous, we can extend them to L ²(0,T;H ¹(Ω₁)) with Ω⊂Ω₁.

Now, we rewrite the weak formulation of the microscopic equation for c ^ε as

$$\begin{array}{@{}rcl@{}} &&\langle \partial_{t} c^{\varepsilon} - F(c^{\varepsilon}), \phi \chi_{{\Omega}_{\varepsilon}^{\ast}} \rangle_{{\Omega}_{T}} + \langle A\nabla c^{\varepsilon}, \nabla \phi \chi_{{\Omega}_{\varepsilon}^{\ast}} \rangle_{{\Omega}_{T}} - \varepsilon \langle \beta^{\varepsilon} r_{b}^{\varepsilon} -\alpha^{\varepsilon} c^{\varepsilon} r_{f}^{\varepsilon}, \phi \rangle_{{\Gamma}^{\varepsilon}_{T}}\\ &&= \left[\langle \partial_{t} c^{\varepsilon} - F(c^{\varepsilon}), \phi \chi_{\widetilde {\Omega}_{\varepsilon}^{\ast}} \rangle_{{\Omega}_{T}} + \langle A\nabla c^{\varepsilon}, \nabla \phi \chi_{\widetilde {\Omega}_{\varepsilon}^{\ast}} \rangle_{{\Omega}_{T}} - \varepsilon \langle \widetilde \beta^{\varepsilon} r_{b}^{\varepsilon} -\widetilde \alpha^{\varepsilon} c^{\varepsilon} r_{f}^{\varepsilon}, \phi \rangle_{\widetilde {\Gamma}^{\varepsilon}_{T}} \right]\\ &&\quad+\left[\langle \partial_{t} c^{\varepsilon} - F(c^{\varepsilon}), \phi (\chi_{{\Omega}_{\varepsilon}^{\ast}}-\chi_{\widetilde {\Omega}_{\varepsilon}^{\ast}}) \rangle_{{\Omega}_{T}} + \langle A\nabla c^{\varepsilon}, \nabla \phi (\chi_{{\Omega}_{\varepsilon}^{\ast}} -\chi_{\widetilde {\Omega}_{\varepsilon}^{\ast}}) \rangle_{{\Omega}_{T}} \right]\\ &&\quad -\varepsilon \left[\langle \beta^{\varepsilon} r_{b}^{\varepsilon} -\alpha^{\varepsilon} c^{\varepsilon} r_{f}^{\varepsilon}, \phi \rangle_{{\Gamma}^{\varepsilon}_{T}} - \langle \widetilde \beta^{\varepsilon} r_{b}^{\varepsilon} -\widetilde \alpha^{\varepsilon} c^{\varepsilon} r_{f}^{\varepsilon}, \phi \rangle_{\widetilde {\Gamma}^{\varepsilon}_{T}} \right]=I_{1} +I_{2} +I_{3} \end{array} $$

for $\phi \in C^{1}(\overline {\Omega }_{T})$. Notice that we use the same notation for c ^ε, $r^{\varepsilon }_{f}$, and $r^{\varepsilon }_{b}$ and their extensions.

The estimates for $\mathcal I_{1}$, $\mathcal I_{2}$, $\mathcal I_{3}$, and $\mathcal I_{4}$, shown above, and similar calculations for the difference of the boundary integrals of $\beta ^{\varepsilon } r_{b}^{\varepsilon }$ and $\widetilde \beta ^{\varepsilon } r_{b}^{\varepsilon }$, respectively, imply that I ₂→0 and I ₃→0 as ε→0. Thus we obtain that

$$\begin{array}{@{}rcl@{}} 0&=&\lim_{\varepsilon \to 0}\left[\langle \partial_{t} c^{\varepsilon}- F(c^{\varepsilon}), \phi \chi_{{\Omega}_{\varepsilon}^{\ast}} \rangle_{{\Omega}_{T}} + \langle A\nabla c^{\varepsilon}, \nabla \phi \chi_{{\Omega}_{\varepsilon}^{\ast}} \rangle_{{\Omega}_{T}} - \varepsilon \langle \beta^{\varepsilon} r_{b}^{\varepsilon} -\alpha^{\varepsilon} c^{\varepsilon} r_{f}^{\varepsilon}, \phi \rangle_{{\Gamma}^{\varepsilon}_{T}} \right]\\ &=& \lim_{\varepsilon \to 0} \left[\langle \partial_{t} c^{\varepsilon} - F(c^{\varepsilon}), \phi \chi_{\widetilde {\Omega}_{\varepsilon}^{\ast}} \rangle_{{\Omega}_{T}} + \langle A\nabla c^{\varepsilon}, \nabla \phi \chi_{\widetilde {\Omega}_{\varepsilon}^{\ast}} \rangle_{{\Omega}_{T}} - \varepsilon \langle \widetilde \beta^{\varepsilon} r_{b}^{\varepsilon} -\widetilde \alpha^{\varepsilon} c^{\varepsilon} r_{f}^{\varepsilon}, \phi \rangle_{\widetilde {\Gamma}^{\varepsilon}_{T}} \right]. \end{array} $$

Similarly, we obtain that

$$\begin{array}{@{}rcl@{}} 0&=&\lim_{\varepsilon \to 0}\varepsilon \langle \partial_{t} r^{\varepsilon}_{f} - p(r_{b}^{\varepsilon}) + \alpha^{\varepsilon} c^{\varepsilon} r_{f}^{\varepsilon} - \beta^{\varepsilon} r_{b}^{\varepsilon} + d_{f} r_{f}^{\varepsilon}, \phi \rangle_{{\Gamma}^{\varepsilon}_{T}}\\ &=& \lim_{\varepsilon \to 0}\varepsilon\langle \partial_{t} r^{\varepsilon}_{f} - p(r_{b}^{\varepsilon}) + \widetilde \alpha^{\varepsilon} c^{\varepsilon} r_{f}^{\varepsilon} -\widetilde \beta^{\varepsilon} r_{b}^{\varepsilon} + d_{f} r_{f}^{\varepsilon}, \phi \rangle_{\widetilde {\Gamma}^{\varepsilon}_{T}}, \\ 0&=&\lim_{\varepsilon \to 0}\varepsilon \langle \partial_{t} r^{\varepsilon}_{b} - \alpha^{\varepsilon} c^{\varepsilon} r_{f}^{\varepsilon} + \beta^{\varepsilon} r_{b}^{\varepsilon} + d_{b} r_{b}^{\varepsilon}, \phi \rangle_{{\Gamma}^{\varepsilon}_{T}}\\ &=& \lim_{\varepsilon \to 0}\varepsilon\langle \partial_{t} r^{\varepsilon}_{b} - \widetilde \alpha^{\varepsilon} c^{\varepsilon} r_{f}^{\varepsilon} + \widetilde \beta^{\varepsilon} r_{b}^{\varepsilon} + d_{b} r_{b}^{\varepsilon}, \phi \rangle_{\widetilde {\Gamma}^{\varepsilon}_{T}} \qquad \text{ for}\,\,\, \phi \in C^{1}(\overline{\Omega}_{T}). \end{array} $$

The definition of $\widetilde {\Omega }_{\varepsilon }^{\ast }$, $\widetilde {\Gamma }^{\varepsilon }$, $\widetilde \alpha ^{\varepsilon }$, and $\widetilde \beta ^{\varepsilon }$ implies that the original non-periodic problem is approximated by equations posed in a domain with locally periodic microstructure. Hence we can apply the methods of locally periodic two-scale convergence (l-t-s) and l-p unfolding operator to derive the limit equations.

Using the extension of c ^ε, we have that the sequences {c ^ε}, {∇c ^ε} and {∂ _t c ^ε} are defined on Ω _T and we can determine $\mathcal T^{\varepsilon }_{\mathcal L} (c^{\varepsilon })$, $\mathcal T^{\varepsilon }_{\mathcal L} (\nabla c^{\varepsilon })$, $\partial _{t} \mathcal T^{\varepsilon }_{\mathcal L} (c^{\varepsilon })$, and $\mathcal T^{b,\varepsilon }_{\mathcal L} (c^{\varepsilon })$. The properties of $\mathcal T^{\varepsilon }_{\mathcal L}$ and $\mathcal T^{b, \varepsilon }_{\mathcal L}$ together with estimates (5a)–(5a) ensure

$$\begin{array}{@{}rcl@{}} \|\mathcal T^{\varepsilon}_{\mathcal L} (c^{\varepsilon})\|_{L^{2}({\Omega}_{T}\times Y)}+\|\mathcal T^{\varepsilon}_{\mathcal L} (\nabla c^{\varepsilon})\|_{L^{2}({\Omega}_{T}\times Y)}+ \|\partial_{t} \mathcal T^{\varepsilon}_{\mathcal L}(c^{\varepsilon}) \|_{L^{2}({\Omega}_{T}\times Y)} &\leq& C,\\ \|\mathcal T^{b,\varepsilon}_{\mathcal L} (c^{\varepsilon})\|_{L^{2}({\Omega}_{T}\times {\Gamma})} + \sum\limits_{j=f,b}\|\mathcal T^{b,\varepsilon}_{\mathcal L} (r_{j}^{\varepsilon})\|_{H^{1}(0,T;L^{2}({\Omega}\times {\Gamma}))} &\leq& C. \end{array} $$

Then, the convergence results for the l-p unfolding operator and l-t-s convergence, see [29, 30] or Appendix, imply that there exist subsequences (denoted again by c ^ε, $r^{\varepsilon }_{f}$ and $r^{\varepsilon }_{b}$) and the functions c∈L ²(0,T;H ¹(Ω)), ∂ _t c∈L ²(Ω _T ), $c_{1} \in L^{2}({\Omega }_{T}; H^{1}_{\text {per}}(\widetilde Y_{x}))$, $r_{f}, r_{b} \in H^{1}(0,T; L^{2}({\Omega }; L^{2} (\widetilde {\Gamma }_{x})))$ such that

$$ \begin{array}{rll} \mathcal T_{\mathcal L}^{\varepsilon}(c^{\varepsilon}) &\to c & \text{ strongly in} \,\,\, L^{2}({\Omega}_{T}; H^{1}(Y)),\\ \partial_{t} \mathcal T_{\mathcal L}^{\varepsilon}(c^{\varepsilon}) &\rightharpoonup \partial_{t} c \quad &\text{ weakly in}\,\,\, L^{2}({\Omega}_{T}\times Y),\\ \mathcal T_{\mathcal L}^{\varepsilon}(\nabla c^{\varepsilon}) &\rightharpoonup \nabla c + D_{x}^{-T} \nabla_{\tilde y} c_{1}(\cdot, D_{x} \cdot) \quad & \text{ weakly in}\,\,\, L^{2}({\Omega}_{T}\times Y), \\ \mathcal T_{\mathcal L}^{b,\varepsilon}(c^{\varepsilon}) &\to c &\text{ strongly in}\,\,\, L^{2}({\Omega}_{T}; L^{2}({\Gamma})), \\ r^{\varepsilon}_{j} &\rightharpoonup r_{j}, \quad \partial_{t} r^{\varepsilon}_{j} \rightharpoonup \partial r_{j} \quad & \text{ l-t-s} ,\quad r_{j}, \partial_{t} r_{j} \in L^{2}({\Omega}_{T}; L^{2}(\widetilde {\Gamma}_{x})), \\ \mathcal T_{\mathcal L}^{b,\varepsilon}(r^{\varepsilon}_{j}) &\rightharpoonup r_{j}(\cdot, \cdot, D_{x} \widetilde K_{x} \cdot) & \text{ weakly in}\,\,\, L^{2}({\Omega}_{T} \times {\Gamma}), \\ \partial_{t} \mathcal T_{\mathcal L}^{b,\varepsilon}(r^{\varepsilon}_{j}) &\rightharpoonup \partial_{t} r_{j}(\cdot,\cdot, D_{x} \widetilde K_{x} \cdot) & \text{ weakly in}\,\,\, L^{2}({\Omega}_{T} \times {\Gamma}), \quad j=f,b. \end{array} $$

(16)

The coefficients $\widetilde \alpha ^{\varepsilon }$ and $\widetilde \beta ^{\varepsilon }$ can be defined as locally periodic approximations of $\widetilde \alpha$ and $\widetilde \beta$, given by (13), i.e.,

$$\widetilde \alpha^{\varepsilon} = \mathcal L^{\varepsilon}(\widetilde \alpha), \qquad \widetilde \beta^{\varepsilon} =\mathcal L^{\varepsilon}(\widetilde \beta) \quad \text{ with}\,\,\, \tilde x_{n}^{\varepsilon} = x_{n}^{\varepsilon}. $$

See Appendix or [29] for the definition of the locally periodic approximation $\mathcal L^{\varepsilon }$. The regularity assumptions on α, β, K, and γ ensure that $\widetilde \alpha$, $\widetilde \beta \in C(\overline {\Omega }; C_{\text {per}}(\widetilde Y_{x}))$.

Considering $\psi ^{\varepsilon }(t, x) =\psi _{1}(t,x) + \varepsilon \mathcal {L}_{\rho }^{\varepsilon }(\psi _{2})(t,x)$, with $\psi _{1} \in C^{1}(\overline {\Omega }_{T})$ and $\psi _{2} \in {C^{1}_{0}}({\Omega }_{T}; C^{1}_{\text {per}}(\widetilde Y_{x}))$, as a test function in (3) (see Appendix or [29] for the definition of $\mathcal {L}_{\rho }^{\varepsilon }$) and applying l-p unfolding operator and l-p boundary unfolding operator imply

$$\begin{array}{@{}rcl@{}} &&\langle \mathcal T_{\mathcal L}^{\varepsilon}(\chi^{\varepsilon}_{\widetilde {\Omega}_{\varepsilon}^{\ast}}) \partial_{t} \mathcal T_{\mathcal L}^{\varepsilon}(c^{\varepsilon}), \mathcal T_{\mathcal L}^{\varepsilon}(\psi^{\varepsilon}) \rangle_{{\Omega}_{T}\times Y} + \langle A \mathcal T_{\mathcal L}^{\varepsilon}(\chi^{\varepsilon}_{\widetilde {\Omega}_{\varepsilon}^{\ast}})\mathcal T_{\mathcal L}^{\varepsilon}(\nabla c^{\varepsilon}), \mathcal T_{\mathcal L}^{\varepsilon}(\nabla \psi^{\varepsilon}) \rangle_{{\Omega}_{T}\times Y} \\ &=&\langle\mathcal T_{\mathcal L}^{\varepsilon}(\chi^{\varepsilon}_{\widetilde {\Omega}_{\varepsilon}^{\ast}}) F(\mathcal T_{\mathcal L}^{\varepsilon}(c^{\varepsilon})), \mathcal T_{\mathcal L}^{\varepsilon}(\psi^{\varepsilon}) \rangle_{{\Omega}_{T}\times Y} \\ &&+ \left\langle \sum\limits_{n=1}^{N_{\varepsilon}} \frac{\sqrt{g_{x_{n}^{\varepsilon}}}}{\sqrt{g}|\widetilde Y_{x_{n}^{\varepsilon}}|} \left[\mathcal T_{\mathcal L}^{b,\varepsilon}(\widetilde \beta^{\varepsilon} r^{\varepsilon}_{b}) - \mathcal T_{\mathcal L}^{b,\varepsilon}(\widetilde \alpha^{\varepsilon}) \mathcal T_{\mathcal L}^{b,\varepsilon} (c^{\varepsilon}) \mathcal T_{\mathcal L}^{b,\varepsilon} (r^{\varepsilon}_{f})\right]\chi_{{\Omega}_{n}^{\varepsilon}}, \mathcal T_{\mathcal L}^{b,\varepsilon}(\psi^{\varepsilon}) \right\rangle_{{\Omega}_{T}\times {\Gamma}}\\ &&-\langle A\nabla c^{\varepsilon}, \nabla\psi^{\varepsilon}\rangle_{{\Lambda}^{\ast}_{\varepsilon},T} \,+\, \langle F(c^{\varepsilon})\,-\, \partial_{t} c^{\varepsilon} , \psi^{\varepsilon}\rangle_{{\Lambda}^{\ast}_{\varepsilon},T} \,+\, \varepsilon \langle \widetilde \beta^{\varepsilon} r_{b}^{\varepsilon} -\widetilde \alpha^{\varepsilon} c^{\varepsilon} r_{f}^{\varepsilon}, \psi^{\varepsilon} \rangle_{\widetilde {\Gamma}^{\varepsilon}\setminus \hat {\Gamma}^{\varepsilon}, T}+\delta(\varepsilon), \end{array} $$

where δ(ε)→0 as ε→0, $\chi ^{\varepsilon }_{\widetilde {\Omega }_{\varepsilon }^{\ast }}=\mathcal L^{\varepsilon }_{0}(\chi _{\widetilde Y_{x,K}^{\ast }})$ and $\chi _{\widetilde Y_{x,K}^{\ast }}$ is the characteristic function of $\widetilde Y^{\ast }_{x,K}$ extended $\widetilde Y_{x}$-periodically to $\mathbb R^{3}$.

The regularity assumptions on γ and K ensure that $\chi _{\widetilde Y_{x,K}^{\ast }} \in L^{\infty }(\bigcup _{x \in {\Omega }}\{ x\} \times \widetilde Y_{x})$ and $\chi _{\widetilde Y_{x,K}^{\ast }} \in C(\overline {\Omega }; L^{p}_{\text {per}}(\widetilde Y_{x}))$ for p∈(1, + ∞).

Applying the results from [30] we obtain $\mathcal T_{\mathcal L}^{\varepsilon }(\chi ^{\varepsilon }_{\widetilde {\Omega }_{\varepsilon }^{\ast }})(x,\tilde y) \to \chi _{\widetilde Y^{\ast }_{x,K}} (x, D_{x} \tilde y)$ in L ^p(Ω×Y) and $\mathcal T_{\mathcal L}^{b,\varepsilon }(\widetilde \beta ^{\varepsilon })(x,\bar y)\to \widetilde \beta (x, D_{x} \widetilde K_{x} \bar y)$, $\mathcal T_{\mathcal L}^{b,\varepsilon }(\widetilde \alpha ^{\varepsilon })(x,\bar y)\to \widetilde \alpha (x, D_{x} \widetilde K_{x} \bar y)$ in L ^p(Ω×Γ) for p∈(1, + ∞), as ε→0.

Using the a priori estimates for c ^ε, $r^{\varepsilon }_{f}$ and $r^{\varepsilon }_{b}$, the strong convergence of $\mathcal T_{\mathcal L}^{\varepsilon }(c^{\varepsilon })$ in L ²(Ω _T ;H ¹(Y)), the strong convergence and boundedness of $\mathcal T_{\mathcal L}^{b,\varepsilon }(\widetilde \alpha ^{\varepsilon })$, the weak convergence and boundedness of $\mathcal T_{\mathcal L}^{b,\varepsilon } (r^{\varepsilon }_{f})$, together with the regularity of D, γ, and K, and the strong convergence of $\mathcal T_{\mathcal L}^{b,\varepsilon }(\psi ^{\varepsilon }),$ we obtain

$$\begin{array}{@{}rcl@{}} &&\lim_{\varepsilon \to 0} \left\langle \sum\limits_{n=1}^{N_{\varepsilon}} \frac{\sqrt{g_{x_{n}^{\varepsilon}}}}{\sqrt{g}|\widetilde Y_{x_{n}^{\varepsilon}}|} \mathcal T_{\mathcal L}^{b,\varepsilon}(\widetilde\alpha^{\varepsilon}) \mathcal T_{\mathcal L}^{b,\varepsilon} (c^{\varepsilon}) \mathcal T_{\mathcal L}^{b,\varepsilon} (r^{\varepsilon}_{f})\chi_{{\Omega}_{n}^{\varepsilon}}, \mathcal T_{\mathcal L}^{b,\varepsilon}(\psi^{\varepsilon}) \right\rangle_{{\Omega}_{T}\times {\Gamma}}\\ &&\quad= \left\langle \frac{\sqrt{g_{x}}}{\sqrt{g} |\widetilde Y_{x}|}\widetilde \alpha(x, D_{x} \widetilde K_{x} \bar y) c(t,x) r_{f} (t,x, D_{x} \widetilde K_{x} \bar y), \psi_{1}(t,x) \right\rangle_{{\Omega}_{T}\times {\Gamma}}. \end{array} $$

Similar arguments along with the Lipschitz continuity of F and the strong convergence of $\mathcal T_{\mathcal L}^{\varepsilon }(\chi ^{\varepsilon }_{\widetilde {\Omega }_{\varepsilon }^{\ast }})$ ensure

$$\langle\mathcal T_{\mathcal L}^{\varepsilon}(\chi^{\varepsilon}_{\widetilde {\Omega}_{\varepsilon}^{\ast}})\, F(\mathcal T_{\mathcal L}^{\varepsilon}(c^{\varepsilon})), \mathcal T_{\mathcal L}^{\varepsilon}(\psi^{\varepsilon}) \rangle_{{\Omega}_{T}\times Y} \to \langle \chi_{\widetilde Y_{x,K}^{\ast}}(x, D_{x} \tilde y) \, F(c), \psi_{1} \rangle_{{\Omega}_{T}\times Y} $$

as ε→0. Using the convergence results (16), the strong convergence of $\mathcal T_{\mathcal L}^{\varepsilon }(\psi ^{\varepsilon })$ and $\mathcal T_{\mathcal L}^{\varepsilon }(\nabla \psi ^{\varepsilon })$ and the fact that $|{\Lambda }^{\ast }_{\varepsilon }| \to 0$ as ε→0, taking the limit as ε→0, and considering the change of variables $y=D_{x} \tilde y$ for $\tilde y \in Y$ and $y = D_{x} \widetilde K_{x} \bar y$ for $\bar y \in {\Gamma }$, we obtain

$$\begin{array}{@{}rcl@{}} &&\langle|\widetilde Y_{x}|^{-1} c , \psi_{1} \rangle_{\widetilde Y^{\ast}_{x,K}\times {\Omega}_{T}} + \langle |\widetilde Y_{x}|^{-1} A (\nabla c + \nabla_{y} c_{1}), \nabla \psi_{1} + \nabla_{y} \psi_{2} \rangle_{\widetilde Y^{\ast}_{x,K}\times {\Omega}_{T}} \\ && + \langle |\widetilde Y_{x}|^{-1} \left[\widetilde \alpha(x, y) r_{f} c -\widetilde \beta(x, y) r_{b}\right], \psi_{1} \rangle_{\widetilde {\Gamma}_{x} \times {\Omega}_{T}} = \langle |\widetilde Y_{x}|^{-1} F(c), \psi_{1} \rangle_{\widetilde Y^{\ast}_{x,K}\times {\Omega}_{T}}. \end{array} $$

Considering ψ ₁(t,x)=0 for (t,x)∈Ω _T , we obtain

$$c_{1}(t,x,y) = \sum\limits_{j=1}^{3} \partial_{x_{j}} c(t,x) w^{j} (x,y), $$

where w ^j are solutions of (12). Choosing ψ ₂(t,x,y)=0 for (t,x)∈Ω _T and $y\in \widetilde Y_{x}$ yields the macroscopic equation for c.

Using the strong convergence of $\mathcal {T}_{\mathcal L}^{b,\varepsilon }(c^{\varepsilon })$ in L ²(Ω _T ;L ²(Γ)), estimates (5a)–(5a) and (6), and the Lipschitz continuity of p we obtain that $\{\mathcal {T}_{\mathcal L}^{b,\varepsilon }(r^{\varepsilon }_{j})\}$ is a Cauchy sequence in L ²(Ω _T ;L ²(Γ)) for j = f,b, and hence upto a subsequence, $\mathcal {T}_{\mathcal L}^{b,\varepsilon }(r^{\varepsilon }_{j}) \to r_{j} (\cdot ,\cdot , D_{x} \widetilde K_{x} \cdot )$ strongly in L ²(Ω _T ;L ²(Γ)). Then applying the l-p boundary unfolding operator to the equations on $\widetilde {\Gamma }^{\varepsilon }$ and taking the limit as ε→0 we obtain the equations for r _f and r _b . The proof of the uniqueness of a solution of the macroscopic problem is similar to the corre- sponding proof for the microscopic problem, and hence the convergence of the whole sequences of solutions of the microscopic problem follows. □

Remark 1

Notice that for the proof of the homogenization results it is sufficient to have a local extension of c ^ε from ${\Omega }_{\varepsilon }^{\ast }$ to Ω^δ, with Ω^δ={x∈Ω:dist(x,∂Ω)>δ} for any fixed δ>0, and hence, the local strong convergence of $\mathcal T_{\mathcal L}^{\varepsilon }(c^{\varepsilon })$, i.e., the strong convergence in $L^{2}(0,T; L^{2}_{\text {loc}}({\Omega }; H^{1}(Y)))$.

Remark 2

For numerical computations of the cell problems (12) and the ordinary differential equations (11), defining the dynamics of receptor densities, approaches from the two-scale finite element method [24] or the heterogeneous multiscale method [1, 2, 17, 18] can be applied.

Appendix: Definition and Convergence Results for the l-t-s Convergence and l-p Unfolding Operator

We shall consider the space $C(\overline {\Omega }; C_{\text {per}}(\widetilde Y_{x}))$ given in a standard way, i.e. for any $\widetilde \psi \in C(\overline {\Omega }; C_{\text {per}}(Y))$ the relation $\psi (x,y)= \widetilde \psi (x, D_{x}^{-1}y)$ with x∈Ω and $y \in \widetilde Y_{x}$ yields $\psi \in C(\overline {\Omega }; C_{\text {per}}(\widetilde Y_{x}))$. In the same way the spaces $L^{p}({\Omega }; C_{\text {per}}(\widetilde Y_{x}))$, $L^{p}({\Omega }; L^{q}_{\text {per}}(\widetilde Y_{x}))$ and $C(\overline {\Omega }; L^{q}_{\text {per}}(\widetilde Y_{x}))$, for 1≤p≤∞, 1≤q<∞, are given.

Due to the assumptions on D, i.e. $D\in \text {Lip}(\overline {\Omega })$ and 0<d ₀≤| detD(x)|≤d ₁<∞ for all $x\in \overline {\Omega }$, we obtain that the function $u: {\Omega } \to C(\widetilde Y_{x})$ is well-defined. The separability of $C_{\text {per}}(\widetilde Y_{x})$ for each x∈Ω and the Weierstrass approximation for continuous functions $u: {\Omega } \to C_{\text {per}}(\widetilde Y_{x})$ ensure the separability of $C(\overline {\Omega }; C_{\text {per}}(\widetilde Y_{x}))$. Also, we have the following relation for the norm $\| \psi \|_{C(\overline {\Omega }; C_{\text {per}}(\widetilde Y_{x}))}:= \sup _{x\in \overline {\Omega }} \sup _{y\in \widetilde Y_{x}} |\psi (x,y)|$:

$$\|\psi\|_{C(\overline {\Omega}; C_{\text{per}}(\widetilde Y_{x}))}= \sup_{x\in \overline{\Omega}} \sup_{y \in \widetilde Y_{x}} |\widetilde \psi(x,D_{x}^{-1}y)| = \sup_{x\in \overline{\Omega}} \sup_{\tilde y\in Y}|\widetilde \psi(x, \tilde y)|. $$

The assumptions on D and K ensure that

$$\begin{array}{@{}rcl@{}} L^{2}({\Omega}; H^{1}(\widetilde Y_{x})) &=& \{ u \in L^{2}({\Omega}; L^{2}(\widetilde Y_{x})), \, \nabla_{y} u \in L^{2}({\Omega}; L^{2}(\widetilde Y_{x})^{3}) \} \quad \text{ and} \\ L^{2}({\Omega}; L^{2}(\widetilde {\Gamma}_{x}))&=& \left\{u:\cup_{x\in {\Omega}} \left(\{x\}\times \widetilde {\Gamma}_{x}\right) \to \mathbb R \,\text{ measurable, with} \right.\\ &&\left.\quad u(x) \in L_{2}(\widetilde {\Gamma}_{x}) \text{ for a.e.}\, x\in {\Omega} \text{ and} {\int}_{\Omega} \|u\|^{2}_{L^{2}(\widetilde {\Gamma}_{x})} dx< \infty\right\} \end{array} $$

are well-defined, separable Hilbert spaces, see e.g. [16, 26, 32].

Consider $\psi \in C(\overline {\Omega }; C_{\text {per}}(\widetilde Y_{x}))$ and corresponding $\widetilde \psi \in C(\overline {\Omega }; C_{\text {per}}(Y))$. As a locally periodic (l-p) approximation of ψ, we name $\mathcal L^{\varepsilon }: C(\overline {\Omega }; C_{\text {per}}(\widetilde Y_{x}))\to L^{\infty }({\Omega })$ given by, see [29],

$$ (\mathcal L^{\varepsilon} \psi)(x) = \sum\limits_{n=1}^{N_{\varepsilon}} \widetilde \psi\left(x, \frac {D^{-1}_{x_{n}^{\varepsilon}}(x-\tilde x_{n}^{\varepsilon})} \varepsilon\right)\chi_{{\Omega}_{n}^{\varepsilon}}(x) \quad \text{ for}\,\, x\in {\Omega}. $$

(17)

We consider also the map $\mathcal L^{\varepsilon }_{0}: C(\overline {\Omega }; C_{\text {per}}(\widetilde Y_{x})) \to L^{\infty }({\Omega })$ defined for x∈Ω as

$$(\mathcal L^{\varepsilon}_{0} \psi)(x)=\sum\limits_{n=1}^{N_{\varepsilon}} \psi\left(x_{n}^{\varepsilon}, \frac {x-\tilde x_{n}^{\varepsilon}}\varepsilon\right)\chi_{{\Omega}_{n}^{\varepsilon}}(x)= \sum\limits_{n=1}^{N_{\varepsilon}} \widetilde \psi\left(x_{n}^{\varepsilon}, \frac {D^{-1}_{x_{n}^{\varepsilon}}(x-\tilde x_{n}^{\varepsilon})}\varepsilon\right)\chi_{{\Omega}_{n}^{\varepsilon}}(x). $$

If we choose $\tilde x_{n}^{\varepsilon } = D_{x_{n}^{\varepsilon }} \varepsilon k$ for some $k \in \mathbb Z^{3}$, then the periodicity of $\widetilde \psi$ implies

$$(\mathcal L^{\varepsilon} \psi)(x) = \sum\limits_{n=1}^{N_{\varepsilon}} \widetilde \psi\left(x, \frac {D^{-1}_{x_{n}^{\varepsilon}}x}\varepsilon\right)\chi_{{\Omega}_{n}^{\varepsilon}}(x), \quad (\mathcal L^{\varepsilon}_{0} \psi)(x) = \sum\limits_{n=1}^{N_{\varepsilon}} \widetilde \psi\left(x_{n}^{\varepsilon}, \frac {D^{-1}_{x_{n}^{\varepsilon}}x} \varepsilon\right)\chi_{{\Omega}_{n}^{\varepsilon}}(x) $$

for x∈Ω, see e.g. [29] for more details. In the similar way, we define $\mathcal L^{\varepsilon }\psi$ and $\mathcal L^{\varepsilon }_{0}\psi$ for ψ in $C(\overline {\Omega }; L^{q}_{\text {per}}(\widetilde Y_{x}))$ or $L^{p}({\Omega }; C_{\text {per}}(\widetilde Y_{x}))$.

We define also a regular approximation of $\mathcal L^{\varepsilon } \psi$

$$(\mathcal L^{\varepsilon}_{\rho} \psi)(x)= \sum\limits_{n=1}^{N_{\varepsilon}} \widetilde \psi\left(x, \frac {D^{-1}_{x_{n}^{\varepsilon}} x}\varepsilon\right)\phi_{{\Omega}_{n}^{\varepsilon}}(x) \quad \text{ for}\,\, x\in {\Omega}, $$

where $\phi _{{\Omega }_{n}^{\varepsilon }}$ are approximations of $\chi _{{\Omega }_{n}^{\varepsilon }}$ such that $\phi _{{\Omega }_{n}^{\varepsilon }} \in C^{\infty }_{0} ({\Omega }_{n}^{\varepsilon })$ and

$$\sum\limits_{n=1}^{N_{\varepsilon}}|\phi_{{\Omega}_{n}^{\varepsilon}} - \chi_{{\Omega}_{n}^{\varepsilon}}| \to 0 \text{ in}\,\, L^{2}({\Omega}),\quad \|\nabla^{m} \phi_{{\Omega}_{n}^{\varepsilon}}\|_{L^{\infty}(\mathbb R^{d})}\leq C \varepsilon^{-\rho m} \text{ for}\,\, 0<r<\rho<1. $$

We recall here the definition of locally periodic two-scale (l-t-s) convergence and l-p unfolding operator, see [29, 30] for details.

Definition 2 (29)

Let u ^ε∈L ^p(Ω) for all ε>0 and 1<p<∞. We say the sequence {u ^ε} converges l-t-s to $u \in L^{p}({\Omega }; L^{p}(\widetilde Y_{x}))$ as ε→0 if $\| u^{\varepsilon }\|_{L^{p}({\Omega })} \leq C$ and for any $\psi \in L^{q}({\Omega }; C_{\text {per}}(\widetilde Y_{x}))$

where $\mathcal L^{\varepsilon }$ is the l-p approximation of ψ and 1/p+1/q=1.

Definition 3 (30)

A sequence $\{u^{\varepsilon }\} \subset L^{p}(\widetilde {\Gamma }^{\varepsilon })$, with 1<p<∞, is said to converge locally periodic two-scale (l-t-s) to $u \in L^{p}({\Omega }; L^{p}(\widetilde {\Gamma }_{x}))$ if

$$\varepsilon \|u^{\varepsilon} \|^{p}_{L^{p}(\widetilde{\Gamma}^{\varepsilon})} \leq C $$

and for any $\psi \in C(\overline {\Omega }; C_{\text {per}}(\widetilde Y_{x}))$

$$\lim_{\varepsilon \to 0} \varepsilon {\int}_{\widetilde{\Gamma}^{\varepsilon}} u^{\varepsilon}(x) \mathcal{L}^{\varepsilon} \psi(x) d\sigma_{x} = {\int}_{\Omega} \frac 1{|\widetilde Y_{x}|} {\int}_{\widetilde {\Gamma}_{x}} u(x,y) \psi(x, y) d\sigma_{y} dx, $$

where $\mathcal {L}^{\varepsilon }$ is the l-p approximation of ψ defined in (17).

Lemma 4 (30)

For $\psi \in C(\overline {\Omega }; C_{\textnormal {per}}(\widetilde Y_{x}))$ and 1≤p<∞, we have that

$$\lim_{\varepsilon \to 0}\varepsilon {\int}_{\widetilde{\Gamma}^{\varepsilon}} |\mathcal{L}^{\varepsilon} \psi (x)|^{p} d\sigma_{x} = {\int}_{\Omega} \frac 1 {|\widetilde Y_{x}|} {\int}_{\widetilde{\Gamma}_{x}} |\psi(x,y)|^{p} d\sigma_{y} dx. $$

Definition 4 (30)

For any Lebesgue-measurable on Ω function ψ the locally periodic unfolding operator (l-p unfolding operator) $\mathcal T_{\mathcal L}^{\varepsilon }$ is defined as

$$\mathcal T^{\varepsilon}_{\mathcal L} (\psi) (x,y) = \sum\limits_{n=1}^{N_{\varepsilon}} \psi\left(\varepsilon D_{x_{n}^{\varepsilon}} \left[{D^{-1}_{x_{n}^{\varepsilon}} x} /\varepsilon \right]_{Y} + \varepsilon D_{x_{n}^{\varepsilon}} y \right) \chi_{\hat {\Omega}_{n}^{\varepsilon}}(x) $$

for x∈Ω and y∈Y.

The definition implies that $\mathcal T_{\mathcal L}^{\varepsilon } (\phi )$ is Lebesgue-measurable on Ω×Y and is zero for x∈Λ^ε, where ${\Lambda }^{\varepsilon }= \bigcup _{n=1}^{N_{\varepsilon }} ({\Omega }_{n}^{\varepsilon } \setminus \hat {\Omega }_{n}^{\varepsilon })\cap {\Omega }$.

Definition 5 (30)

For any Lebesgue-measurable on $\widetilde {\Gamma }^{\varepsilon }$ function ψ the l-p boundary unfolding operator $\mathcal T_{\mathcal L}^{b,\varepsilon }$ is defined as

$$\mathcal T^{b,\varepsilon}_{\mathcal L} (\psi) (x,y) = \sum\limits_{n=1}^{N_{\varepsilon}} \psi\left(\varepsilon D_{x_{n}^{\varepsilon}} \big[ {D^{-1}_{x_{n}^{\varepsilon}} x}/ \varepsilon\big]_{Y} + \varepsilon D_{x_{n}^{\varepsilon}}\widetilde K_{x_{n}^{\varepsilon}} y \right) \chi_{\hat {\Omega}_{n}^{\varepsilon}}(x) $$

for x∈Ω and y∈Γ.

These definitions provide a generalization of the periodic unfolding operator and periodic boundary unfolding operator introduced in [12–14] to locally periodic microstructures.

Theorem 2 (30)

For a sequence {w ^ε }⊂L ^p (Ω), with p∈(1,∞), satisfying

$$\|w^{\varepsilon} \|_{L^{p}({\Omega})} + \varepsilon \|\nabla w^{\varepsilon} \|_{L^{p}({\Omega})} \leq C $$

there exist a subsequence (denoted again by {w ^ε }) and $w \in L^{p}({\Omega }; W^{1,p}_{\textnormal {per}}(\widetilde Y_{x}))$ such that

$$\begin{array}{rll} \mathcal{T}_{\mathcal L}^{\varepsilon}(w^{\varepsilon}) &\rightharpoonup w(\cdot, D_{x} \cdot) \quad& \text{ weakly in}\,\,\, L^{p}({\Omega}; W^{1,p}(Y)), \\ [5pt] \varepsilon \mathcal{T}_{\mathcal L}^{\varepsilon}(\nabla w^{\varepsilon}) &\rightharpoonup D_{x}^{-T}\nabla_{y} w(\cdot, D_{x} \cdot) \quad & \text{ weakly in} \,\,\, L^{p}({\Omega}\times Y). \end{array} $$

Theorem 3 (30)

For a sequence {w ^ε }⊂W ^1,p (Ω), with p∈(1,∞), that converges weakly to w in W ^1,p (Ω), there exist a subsequence (denoted again by {w ^ε }) and a function $w_{1}\in L^{p}({\Omega }; W^{1,p}_{\textnormal {per}}(\widetilde Y_{x}))$ such that

$$\begin{array}{rll} \mathcal T_{\mathcal L}^{\varepsilon}(w^{\varepsilon}) & \rightharpoonup w & \text{ weakly in}\,\,\, L^{p}({\Omega}; W^{1,p}(Y)), \\ [5pt] \mathcal T_{\mathcal L}^{\varepsilon}(\nabla w^{\varepsilon})(\cdot, \cdot) & \rightharpoonup \nabla_{x} w(\cdot) + D_{x}^{-T} \nabla_{y} w_{1}(\cdot, D_{x} \cdot) & \text{ weakly in}\,\,\, L^{p}({\Omega}\times Y). \end{array} $$

Theorem 4 (30)

For a sequence $\{ w^{\varepsilon } \} \subset L^{p}(\widetilde {\Gamma }^{\varepsilon })$ , with p∈(1,∞), satisfying

$$\varepsilon \| w^{\varepsilon}\|^{p}_{L^{p}(\widetilde {\Gamma}^{\varepsilon})}\leq C $$

there exist a subsequence (denoted again by {w ^ε }) and $w \in L^{p}({\Omega }; L^{p}(\widetilde {\Gamma }_{x}))$ such that

$$w^{\varepsilon} \to w \quad \text{ locally periodic two-scale (l-t-s)}. $$

Theorem 5 (30)

Let $\{ w^{\varepsilon }\} \subset L^{p}(\widetilde {\Gamma }^{\varepsilon })$ with $\varepsilon \| w^{\varepsilon } \|^{p}_{L^{p}(\widetilde {\Gamma }^{\varepsilon })} \leq C$, where p∈(1,∞). The following assertions are equivalent

• (i) w ^ε →w l-t-s, $w \in L^{p}({\Omega }; L^{p}(\widetilde {\Gamma }_{x}))$.

• (ii) $\mathcal {T}_{\mathcal L}^{b, \varepsilon } (w^{\varepsilon }) \rightharpoonup w(\cdot , D_{x}\widetilde K_{x} \cdot )$ weakly in L ^p(Ω×Γ).

Theorems 4 and 5 imply that for $\{ w^{\varepsilon }\} \subset L^{p}(\widetilde {\Gamma }^{\varepsilon })$ with $\varepsilon \| w^{\varepsilon } \|^{p}_{L^{p}(\widetilde {\Gamma }^{\varepsilon })} \leq C$ we have the weak convergence of $\{\mathcal {T}_{\mathcal L}^{b, \varepsilon } (w^{\varepsilon })\}$ in L ^p(Ω×Γ), where p∈(1,∞).