1 Introduction

For a successful transition from fossil fuels to less CO2 emissions, an increase in energy from renewable sources will be crucial. Wind energy takes on a leading role, showing a trend towards larger and more efficient Wind Turbines (WT) over the last decades. Aside from larger and more efficient turbines, regulations for new turbine sites reduce the expansion of this technology significantly. Such strict regulations intend to reduce the negative impact of acoustic emissions from WT for residents nearby. To increase the amount of potential areas for wind energy, the acoustic emissions of new turbines must be reduced. In order to achieve this reduction, developers aim to simulate the acoustic emissions of a WT early in the development process and optimize the WT accordingly.

To reduce acoustic emissions of a WT, the source of the vibrations (e.g. blades, gearbox), the emitting surfaces (e.g. blades, tower and nacelle cover) and the transmission between source and surface have to be studied. The focus of this paper lies on a method to identify relevant transfer paths between the WT drivetrain and the emitting surfaces. The identified transfer paths can be used to improve turbine acoustics, especially in problematic transmission areas.

To study the transmission of the vibration, the system is separated into an active side, which contains one or multiple excitations, and a passive side, which contains a reference point, point of interest or surface of radiation ([1]; see Fig. 1).

Fig. 1
figure 1

Transfer path between active and passive side

Full size image

The transfer characteristics of the coupled system is expressed as a result of the frequency response function (\(FRF_{ki}\)) multiplied with the interface force \(F_{i}\) at the coupling points (Eq. 1; [2, 4]).

$$y_{k}=\sum _{i=1}^{n}\mathrm{FRF}_{ki}\cdot F_{i}$$
(1)

The FRF describes the relation at a reference point y to an excitation at point x. The excitation is normally a force acting at the coupling point, while the answer y can be a force, an acceleration or sound pressure. Both values are given in the complex frequency domain.

$$FRF=\frac{Y\left(f\right)}{X\left(f\right)}$$
(2)

The FRF for a classical TPA are measured for the passive system with shaker or hammer excitation close to the coupling points and accelerometers at various position on the structure. This method of determining the frequency response of the system requires an extensive testing procedure. If there is no room to place sensors close to the transfer path or if the structure is too large to apply sufficient excitation with a hammer or shaker to receive an answer signal, the measurement of a FRF may yield insufficient results.

The operational transfer path analysis (OTPA) is based on the estimation of the transmissibility matrix from operational measurements [1]. Contrary to the FRF, the Transmissibility Matrix \(H_{ki}\) can be determined using a H1-estimation. In comparison to a classical TPA, the OTPA estimates the transfer path in an assembled system using operation data. It considers the transmissibility at the connector points for different speeds and can factor in the contribution of different source excitations of the drivetrain in one measurement. A key factor for a successful OTPA is the identification of all necessary indicator points around the source and close to the connector points [1]. With a multi-body-simulation-model (MBS model), easy access to the necessary measuring points with virtual sensors is possible. This allows to apply and validate the method and necessary measurement points, not being restricted by the physical limitations of the structure or expensive measurement campaigns.

With the resulting transmissibility matrix, a complete map for the transmission of the vibrations to a receiver point can be visualized and the dominant transfer path can be identified.

2 Operational transfer path method

In the following Chap. 2.2 and 2.3, the method for the operational transfer path analysis is introduced. The method is applied for the wind turbine model described in Chap. 2.1.

The aim of TPA is to study the transmission of vibrations over different coupling points from one structure to another [1]. The method separates the transmission characteristics from the excitation. The system is therefore divided in an active part, which contains the excitation (gearbox, generator, blades) and a passive part, which contains the surface of radiation or point of interest. With measurement points along the coupling points and along the passive structure, the path contribution of the individual path can be calculated.

The method is applied to results obtained from an MBS model of a wind turbine described in Chap. 2.1. An OTPA is applied to be able to validate the results with measurements from a turbine. This circumvents the need for a time-consuming and difficult measurement of FRF by determining the transfer characteristics with a transmissibility matrix obtained by operational measurements [1].

2.1 Simulation model

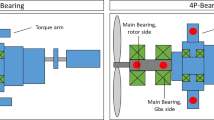
The MBS-model of a 3 MW WT is simulated using SIMPACK. In the model the gearbox in the drivetrain consists of two planetary stages and one spur gear stage. Concerning the drivetrain, all gears of the three stages are simulated flexible as well as the gearbox housing itself. Furthermore, the blades and the tower are included in the model as flexible bodies. The setup of the model is represented in Fig. 2.

Fig. 2
figure 2

Network of WEA Model with Transfer path

Full size image

The drive train is connected to the mainframe by a three-point main bearing arrangement. The bearings themselves are simulated by global stiffness and damping. The connection of the generator with the mainframe is reduced to one centred coupling point even though it is connected in a WT with four mounts. One coupling point of the generator fits the aim to identify the relevant acoustic transfer paths. In total, four transfer paths were considered, one for the rotor bearing, two transfer paths for the gearbox bushing and one over the generator mounts.

2.2 Frequency domain

In a first step, measurement or simulation data is translated from time domain into frequency domain. For this, a Fast-Fourier-transformation (FFT), see Eq. 3, is applied to defined segments of the signal depending on the rotation [3]. A Hanning window without overlapping segments is considered. The resulting complex signal represents the amplitude and phase of the measured data as a function of the frequency. According to the Shannon sampling theorem only the results for half of the sampling frequency can be considered. For this model, a frequency range of interest from 20 to 1000 Hz is observed. Thus, an analysis of the signal at certain frequencies of interest, e.g. tooth mesh frequencies or eigenmodes, can be conducted.

$$S_{d}\left(f_{d}\right)=\sum _{n=0}^{N-1}s_{d}\left(t_{d}\right)\cdot e^{-i2\pi \cdot {f_{d}}{t_{d}}}$$
(3)

2.3 Transmissibility matrix

For a linearized model, the relation between a set of input and output signals can be described with the following Eq. 4:

$$H\left(f\right)\cdot x\left(f\right)=y(f)$$
(4)

In this equation \(H(f)\) stands for the transfer function, or transmissibility matrix, while vector \(x(f)\) represents the input signals, the vector \(y(f)\) the output signals. Both input and output vector can describe motion, typically acceleration \(a_{i}\), forces \(F_{i}\) or sound pressure \(p_{i}.\) For a transfer path analysis the input signals consist of the forces at the transfer path in three coordinates (\(m\)), while the output signal (\(k\)) typically is described by the acceleration of a reference point in two directions or the sound pressure [2, 3].

$$\left[\begin{array}{ccc} H_{11} & \ldots & H_{1m}\\ \vdots & \ddots & \vdots \\ H_{k1} & \ldots & H_{km} \end{array}\right]\cdot \left[\begin{array}{c} x^{\left(1\right)}\\ \vdots \\ x^{\left(m\right)} \end{array}\right]=\left[\begin{array}{c} \begin{array}{c} y^{\left(1\right)}\\ \ldots \\ y^{\left(k\right)} \end{array} \end{array}\right]$$
(5)

For one measurement, the transfer function would only describe the system behavior linearized for one operation point. But the transmissibility matrix aims to describe the systems relation for over different operational points. This adds another dimension to the matrix and a coherence factor µ, which describes the quality of the transmissibility matrix H [2]:

$$\left[\begin{array}{ccc} H_{11} & \ldots & H_{1m}\\ \vdots & \ddots & \vdots \\ H_{k1} & \ldots & H_{km} \end{array}\right]\cdot \left[\begin{array}{ccc} x_{1}^{\left(1\right)} & \ldots & x_{r}^{\left(1\right)}\\ \vdots & \ddots & \vdots \\ x_{1}^{\left(m\right)} & \ldots & x_{r}^{\left(m\right)} \end{array}\right]=\left[\begin{array}{ccc} y_{1}^{\left(1\right)} & \ldots & y_{r}^{\left(1\right)}\\ \vdots & \ddots & \vdots \\ y_{1}^{\left(k\right)} & \ldots & y_{r}^{\left(k\right)} \end{array}\right]-\left[\begin{array}{c} \mu ^{\left(1\right)}\\ \vdots \\ \mu ^{\left(k\right)} \end{array}\right]$$
(6)
$$H\cdot X=Y-\mu$$
(7)

The given equation is solved for every frequency individually. To solve this problem, the Eq. 6 is multiplied with the complex conjugate transpose \(X^{T}\). The coherence value is considered to be zero. This results in a least square estimation [2].

$$H=YX^{T}\cdot \left(XX^{T}\right)^{-1}$$
(8)

This equation can also be written as quotient from the Auto Power Spectrum (APS) and Cross Power Spectrum (CPS) with each spectrum averaged by the numbers of considered operational points [2, 3].

$$H=G_{yx}G_{xx}^{-1}$$
(9)
$$G_{xx}=\frac{1}{r}XX^{T}$$
(10)
$$G_{yx}=\frac{1}{r}YX^{T}$$
(11)

This method equals the multi-output-multi-input method to determine the FRF for classical TPA. To calculate the APS/CPS, the Term \(X^{T}X\) is divided with the number of measurements r. This is canceled out when calculating the Transmissibility matrix (Eq. 9; [3]).

2.3.1 Coherence function

The multiple coherence function for the transmissibility matrix (Eq. 12) can give an impression of the accuracy of the results, with \(\left[H\right]^{T}\) being the complex conjugate of H. The coherence function will take a value between 0 and 1, with 1 being full coherence, while a coherence of 0 indicates random noise.

$$\mu _{y\colon x}^{2}\left(f\right)=\frac{\left\lfloor H\right\rfloor \left[G_{xx}\right]\left\lfloor H\right\rfloor ^{T}}{G_{yy}}$$
(12)

2.4 Path contribution plot

To determine the path contribution of each transfer path, the transmissibility matrix is multiplied with the force acting upon the transfer paths. The result shows the path contribution. The sum over all path denotes the total excitation at the reference point (Eq. 13; [4]).

$$y_{k}=\sum _{i=1}^{m}H_{ki}\cdot F_{i}$$
(13)

The results can be plotted in a Partial Path Contribution Plot (PPCP). This graph shows the path contribution and the sum over all path, either in relation to an operation point (e.g. speed), or for a specific operation point in relation to frequency or an order. The path contribution is shown as color plot in logarithmic scale.

3 Transfer path analysis results

The measurements are based on a run-up simulation of the drivetrain between 650 and 1450 rpm with a constant nominal load. The run-up is divided into multiple blocks, which represent individual operation points (n_rot). The measurements were simulated with a sampling rate of 5000 Hz. The acceleration at each considered transfer path was measured in m/s2 in relation to the initial system of the nacelle. In addition, the forces of each mount were measured also using the same reference system. For applications, when the force cannot be measured at a TP directly, the interface forces can also be estimated with the stiffness of the connection point. The measurement was performed for each Transfer Path (rotor bearing, gearbox bushing left and right, generator mount) in each direction of the coordinate system (TP 1–12). The target location (reference point) is a sensor connected to the centre of the tower structure below the yaw bearing, which measures the acceleration in 3 direction (RP 1–3).

3.1 Path contributions

For the application of the OTPA, described in Chap. 2, every considered block of the run-up measurement is set to describe one point of operation. The rotational speed and loads over one block are assumed to be constant. Therefore, the measurement is divided into 60 Blocks, with each measurement block spanning over 0.25 s. That results in 1250 samples per block and a frequency resolution of 4 Hz. The frequency resolution is enough to apply the method and examine the results, with adequate calculation time. For a higher frequency resolution, a different block size or longer measurement can be applied.

The graphs in Fig. 3 picture the simulation results at the gearbox for the rotational block at nominal speed. The first graph is the acceleration for RP 2 in time domain, the second graph shows the same measurement transformed in frequency domain. In the frequency domain, excitations corresponding with distinct vibration sources like tooth mesh frequencies from the gearbox are visible.

Fig. 3
figure 3

Simulation results in time and frequency domain

Full size image

3.1.1 Partial path contribution plot

The path contribution and total path are shown in the following graphs (Fig. 4). The transfer paths 1, 4 and 7 have compared to the other TP a low impact on the vibrations. The graphs show that the main contribution path for this model are the TP 3 and 6, as well as the TP 10–12. The TP 10–12 are more dominant at low speeds, while the TP 3 and 6 show higher relevance in higher speeds.

Fig. 4
figure 4

Partial Path Contribution Plot for a RP1, b RP2, c RP3

Full size image

The Path contribution can also be observed at individual operating point for different frequencies or as Order plot. The path contribution for one rotational speed is given in Fig. 5. It can be observed, that for these conditions, the main transfer path at lower frequencies (<400 Hz) is over the TP 3, 9 and 11. For higher frequencies, the relevant transfer path is almost exclusively the TP11. In the plot in Fig. 5, peaks for certain frequencies can be observed. For example, at 550 Hz and at 680 Hz TP 3 and TP 6 are more relevant, while at 450 Hz the TP 10 has more contribution to the reference point.

Fig. 5
figure 5

Partial path contribution plot for one operation point

Full size image

3.2 Transmissibility matrix

The transmissibility matrix is represented in Fig. 6 for transfer path 1–3. The amplitude of the transmissibility matrix is logarithmically scaled.

Fig. 6
figure 6

Transmissibility Matrix H (a–c) and Coherence (d)

Full size image

The graph in Fig. 6 for TP1 shows a much higher amplitude than the amplitude of the transmissibility matrix for TP 2 and 3. The reason for that is not a higher mobility between the TP 1 and the reference point, but a much lower interface force acting upon that TP.

The coherence for the transmissibility matrix shown in Fig. 6d has a value of \(\mu >0.8\) for all frequencies. This can be considered as good coherence of the transmissibility matrix [3]. The lowest value is at 53 Hz with 0.803. At frequencies over 300 Hz, the transmissibility matrix shows almost full coherence.

In Fig. 7 the transmissibility matrix \(H_{32}\) (H from TP 2 to RP 3) is plotted. With the linear axis of the transmissibility matrix, three peaks are clearly visible. These peaks coincide with the Eigen modes of the mainframe, which show high mobility between the TP 2 and the reference point.

Fig. 7
figure 7

Transmissibility Matrix H32

Full size image

4 Conclusion and outlook

The method described in Chap. 2 enables an examination of transfer paths in a wind turbine based on an MBS model. The acoustic analysis of the model is based on results from an MBS simulation, but can be applied for simulation results as well as for measurements of actual turbine data. With the force acting on the transfer path and measured accelerations for one or multiple reference points, the path contribution of each path can be estimated and plotted. The computed coherence factor proves the transmissibility matrix is coherent for all frequencies. The results can be examined for single operating points or frequency bands in detail, if the transfer path analysis indicates areas of special interest.

For further investigation of transfer path behavior in wind turbines, the simulation model will be validated with turbine measurement.

In addition, the method can be extended with an approach to calculate the interface force on the transfer path with a matrix inversion method from multiple additional measurements.