Skip to main content
SpringerLink
Log in

Lower face cephalometry based on quadrilateral analysis with cone-beam computed tomography: a clinical pilot study

  • Original Article
  • Published:
Oral and Maxillofacial Surgery Aims and scope Submit manuscript

Abstract

Objective

As most orthognathic surgeries focus on the lower face, the aim of this study was to transfer previously developed two-dimensional cephalometry—which is useful for surgeons in the orthognathic surgery of the lower face—to three-dimensional (3D) cephalometry by using cone-beam computed tomography (CBCT). We selected the quadrilateral lower face analysis developed by the surgeon Di Paolo, who focused only for the lower face and mentioned that data in millimeters are more easy to use than angles for surgeons. Additionally, we wanted to create a 3D lower face analysis approach based on quadrilateral analysis and establish a reference table for surgical planning.

Study design

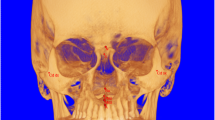
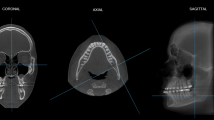
Three investigators assigned 16 landmarks on CBCT images from 30 patients with normocclusion. Intra-class correlation coefficients (ICCs) and standard deviations (SDs) were calculated according to each landmark. The maxillary and mandibular lengths and widths and the anterior and posterior lower facial heights (ALFH and PLFH) are presented as means and SDs. The asymmetry of the face was calculated with paired t test, and the coherence of the lower face was assessed with correlation coefficients (r) and regression models.

Results

The ICCs were ≥0.90, and the SDs of the landmarks were lower than 1.00 mm, except for the J-point, which was located at the junction of the anterior border of the ramus and the corpus of the mandible. The SDs of linear measurements were 3.06–5.20 mm, and there was no significant facial asymmetry. The r among the structures was greater than 0.3 in 13 of 15 assessments. Based on these values, we could establish a floating norm of the lower face using the following five regressions: one linear regression for the mandibular length, two quadratic models for the ALFH and PLFH, and two multivariate regressions for the posterior widths of the maxillae and mandible.

Conclusion

The adaptation of quadrilateral analysis can provide accurate 3D characterization of the morphology of the lower face and the floating norm based on millimeter values, which is practical for surgeons. As the 3D extension of quadrilateral analysis could provide references of the lower face, which might be an accurate 3D approach for presurgical planning, the further investigation in bigger sample would be relevant in the practice.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Papadopoulos MA, Jannowitz C, Boettcher P, Henke J, Stolla R, Zeilhofer HF, Kovacs L, Erhardt W, Biemer E, Papadopulos NA (2005) Three-dimensional fetal cephalometry: an evaluation of the reliability of cephalometric measurements based on three-dimensional CT reconstructions and on dry skulls of sheep fetuses. Journal of Cranio-Maxillo-Facial Surgery: Official Publication of the European Association for Cranio-Maxillo-Facial Surgery 33(4):229–237. doi:10.1016/j.jcms.2005.02.003

    Article  Google Scholar 

  2. Sicurezza E, Greco M, Giordano D, Maiorana F, Leonardi R (2012) Accuracy of landmark identification on postero-anterior cephalograms. Prog Orthod 13(2):132–140. doi:10.1016/j.pio.2011.10.003

    Article  PubMed  Google Scholar 

  3. Silva MA, Wolf U, Heinicke F, Bumann A, Visser H, Hirsch E (2008) Cone-beam computed tomography for routine orthodontic treatment planning: a radiation dose evaluation. American Journal of Orthodontics and Dentofacial Orthopedics: Official Publication of the American Association of Orthodontists, its constituent societies, and the American Board of Orthodontics 133(5):640.e641–640.e645. doi:10.1016/j.ajodo.2007.11.019

    Article  Google Scholar 

  4. Chau AC, Fung K (2009) Comparison of radiation dose for implant imaging using conventional spiral tomography, computed tomography, and cone-beam computed tomography. Oral Surgery, Oral Medicine, Oral Pathology, Oral Radiology, and Endodontics 107(4):559–565. doi:10.1016/j.tripleo.2008.11.009

    Article  PubMed  Google Scholar 

  5. De Vos W, Casselman J, Swennen GR (2009) Cone-beam computerized tomography (CBCT) imaging of the oral and maxillofacial region: a systematic review of the literature. Int J Oral Maxillofac Surg 38(6):609–625. doi:10.1016/j.ijom.2009.02.028

    Article  CAS  PubMed  Google Scholar 

  6. Zamora N, Llamas JM, Cibrian R, Gandia JL, Paredes V (2012) A study on the reproducibility of cephalometric landmarks when undertaking a three-dimensional (3D) cephalometric analysis. Medicina oral, patologia oral y cirugia bucal 17(4):e678–e688

    Article  PubMed  PubMed Central  Google Scholar 

  7. Kim S (2010) Cone beam computed tomography (CBCT) dosimetry: measurements and Monte Carlo simulations. Dissertation, Duke University

  8. Cattaneo PM, Melsen B (2008) The use of cone-beam computed tomography in an orthodontic department in between research and daily clinic. World Journal of Orthodontics 9(3):269–282

    PubMed  Google Scholar 

  9. Gribel BF, Gribel MN, Frazao DC, McNamara JA Jr, Manzi FR (2011a) Accuracy and reliability of craniometric measurements on lateral cephalometry and 3D measurements on CBCT scans. The Angle Orthodontist 81(1):26–35. doi:10.2319/032210-166.1

    Article  PubMed  Google Scholar 

  10. Pittayapat P, Bornstein MM, Imada TS, Coucke W, Lambrichts I, Jacobs R (2015) Accuracy of linear measurements using three imaging modalities: two lateral cephalograms and one 3D model from CBCT data. Eur J Orthod 37:202–208. doi:10.1093/ejo/cju036

    Article  PubMed  Google Scholar 

  11. Gribel BF, Gribel MN, Manzi FR, Brooks SL, McNamara JA Jr (2011b) From 2D to 3D: an algorithm to derive normal values for 3-dimensional computerized assessment. The Angle Orthodontist 81(1):3–10. doi:10.2319/032910-173.1

    Article  PubMed  Google Scholar 

  12. Di Paolo RJ, Philip C, Maganzini AL, Hirce JD (1984) The quadrilateral analysis: a differential diagnosis for surgical orthodontics. Am J Orthod 86(6):470–482

    Article  CAS  PubMed  Google Scholar 

  13. Di Paolo RJPC, Maganzini AL, Hirce JD (1983) The quadrilateral analysis: an individualized skeletal assessment. Am J Orthod 83(1):19–32

    Article  CAS  PubMed  Google Scholar 

  14. Lou L, Lagravere MO, Compton S, Major PW, Flores-Mir C (2007) Accuracy of measurements and reliability of landmark identification with computed tomography (CT) techniques in the maxillofacial area: a systematic review. Oral Surgery, Oral Medicine, Oral Pathology, Oral Radiology, and Endodontics 104(3):402–411. doi:10.1016/j.tripleo.2006.07.015

    Article  PubMed  Google Scholar 

  15. Segner D, Hasund A (1998) Individualisierte Kephalometrie, 3rd edn. Dietmar Segner Verlag, Hamburg

    Google Scholar 

  16. Di Paolo RJ (1970) Cephalometric diagnosis using the quadrilateral analysis. J Clin Orthod 4:30–35

    CAS  PubMed  Google Scholar 

  17. Di Paolo RJ (1969) The quadrilateral analysis: cephalometric analysis of the lower face. J Clin Orthod 3(10):523–530

  18. Lagravere MO, Low C, Flores-Mir C, Chung R, Carey JP, Heo G, Major PW (2010) Intraexaminer and interexaminer reliabilities of landmark identification on digitized lateral cephalograms and formatted 3-dimensional cone-beam computerized tomography images. American Journal of Orthodontics and Dentofacial Orthopedics: Official Publication of the American Association of Orthodontists, its constituent societies, and the American Board of Orthodontics 137(5):598–604. doi:10.1016/j.ajodo.2008.07.018

    Article  Google Scholar 

  19. Weinberg H, Kronman JH (1966) Orthodontic influence upon anterior facial height. The Angle Orthodontist 36(1):80–88. doi:10.1043/0003-3219(1966)036<0080:oiuafh>2.0.co;2

    CAS  PubMed  Google Scholar 

  20. Scheideman GB, Bell WH, Legan HL, Finn RA, Reisch JS (1980) Cephalometric analysis of dentofacial normals. Am J Orthod 78(4):404–420

    Article  CAS  PubMed  Google Scholar 

  21. Bayome M, Park JH, Kook YA (2013) New three-dimensional cephalometric analyses among adults with a skeletal class I pattern and normal occlusion. Korean Journal of Orthodontics 43(2):62–73. doi:10.4041/kjod.2013.43.2.62

    Article  PubMed  PubMed Central  Google Scholar 

  22. Wang MF, Otsuka T, Akimoto S, Sato S (2013) Vertical facial height and its correlation with facial width and depth: three dimensional cone beam computed tomography evaluation based on dry skulls. International Journal of Stomatology & Occlusion Medicine 6:120–129. doi:10.1007/s12548-013-0089-4

    Article  Google Scholar 

  23. Severt TR, Proffit WR (1997) The prevalence of facial asymmetry in the dentofacial deformities population at the University of North Carolina. The International Journal of Adult Orthodontics and Orthognathic Surgery 12(3):171–176

    CAS  PubMed  Google Scholar 

  24. Samman N, Tong AC, Cheung DL, Tideman H (1992) Analysis of 300 dentofacial deformities in Hong Kong. The International Journal of Adult Orthodontics and Orthognathic Surgery 7(3):181–185

    CAS  PubMed  Google Scholar 

  25. de Moraes ME, Hollender LG, Chen CS, Moraes LC, Balducci I (2011) Evaluating craniofacial asymmetry with digital cephalometric images and cone-beam computed tomography. American Journal of Orthodontics and Dentofacial Orthopedics: Official Publication of the American Association of Orthodontists, its constituent societies, and the American Board of Orthodontics 139(6):e523–e531. doi:10.1016/j.ajodo.2010.10.020

    Article  Google Scholar 

  26. Farkas LG, Cheung G (1981) Facial asymmetry in healthy North American Caucasians: an anthropometrical study. Angle Orthod 51(1):70–77

  27. Levine M, Ensom MH (2001) Post hoc power analysis: an idea whose time has passed? Pharmacotherapy 21(4):405–409

    Article  CAS  PubMed  Google Scholar 

  28. Hoenig JM, Heisey DM (2001) The abuse of power: the pervasive fallacy of power calculations for data analysis. Am Stat 55(1):19–24

    Article  Google Scholar 

  29. Lundstrom F, Leighton BC, Richardson A, Lundstrom A (1998) A proportional analysis of some facial height and depth variables in 10 to 16 year old children. Eur J Orthod 20(1):35–44

    Article  CAS  PubMed  Google Scholar 

  30. Franchi L, Baccetti T, McNamara JA Jr (1998) Cephalometric floating norms for North American adults. The Angle Orthodontist 68(6):497–502. doi:10.1043/0003-3219(1998)068<0497:cfnfna>2.3.co;2

    CAS  PubMed  Google Scholar 

  31. Bingmer M, Ozkan V, Jo JM, Lee KJ, Baik HS, Schneider G (2010) A new concept for the cephalometric evaluation of craniofacial patterns (multiharmony). Eur J Orthod 32(6):645–654. doi:10.1093/ejo/cjp152

    Article  PubMed  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Oro-Maxillofacial Surgery and Stomatology, Semmelweis University, Mária Street 52, Budapest, 1085, Hungary

    Adrienn Dobai, Tamás Vizkelety & József Barabás

  2. Kandó Kálmán Faculty of Electrical Engineering, Óbuda University, Tavaszmező Street 15-17, Budapest, 1084, Hungary

    Zsolt Markella

  3. Dento-Cura Kft. Private Praxis, Kálvin Square 3, Budapest, 1053, Hungary

    Adrienne Rosta & Ágnes Kucsera

Authors
  1. Adrienn Dobai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tamás Vizkelety
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zsolt Markella
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Adrienne Rosta
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ágnes Kucsera
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. József Barabás
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Adrienn Dobai.

Ethics declarations

The study was approved by the ethics committee of our institution (approval number: TUKEB 2/2008).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dobai, A., Vizkelety, T., Markella, Z. et al. Lower face cephalometry based on quadrilateral analysis with cone-beam computed tomography: a clinical pilot study. Oral Maxillofac Surg 21, 207–218 (2017). https://doi.org/10.1007/s10006-017-0620-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10006-017-0620-7

Keywords

Search

Navigation