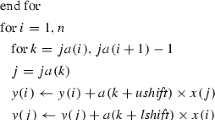Skip to main content
SpringerLink
Log in

Newton-Krylov-FAC methods for problems discretized on locally refined grids

  • Regular Article
  • Published:
Computing and Visualization in Science

Abstract

Many problems in computational science and engineering are nonlinear and time-dependent. The solutions to these problems may include spatially localized features, such as boundary layers or sharp fronts, that require very fine grids to resolve. In many cases, it is impractical or prohibitively expensive to resolve these features with a globally fine grid, especially in three dimensions. Adaptive mesh refinement (AMR) is a dynamic gridding approach that employs a fine grid only where necessary to resolve such features. Numerous AMR codes exist for solving hyperbolic problems with explicit time stepping and some classes of linear elliptic problems. Researchers have paid much less attention to the development of AMR algorithms for the implicit solution of systems of nonlinear equations.

Recent efforts encompassing a variety of applications demonstrate that Newton-Krylov methods are effective when combined with multigrid preconditioners. This suggests that hierarchical methods, such as the Fast Adaptive Composite grid (FAC) method of McCormick and Thomas, can provide effective preconditioning for problems discretized on locally refined grids. In this paper, we address algorithm and implementation issues for the use of Newton-Krylov-FAC methods on structured AMR grids. In our software infrastructure, we combine nonlinear solvers from KINSOL and PETSc with the SAMRAI AMR library, and include capabilities for implicit time stepping. We have obtained convergence rates independent of the number of grid refinement levels for simple, nonlinear, Poisson-like, problems. Additional efforts to employ this infrastructure in new applications are underway.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Almgren, A.S., Bell, J.B., Colella, P., Howell, L.H., Welcome, M.L.: A conservative adaptive projection method for variable density incompressible Navier-Stokes equations. J. Comput. Phys. 142, 1–46 (1998)

    Article  Google Scholar 

  2. Balay, S., Buschelman, K., Gropp, W.D., Kaushik, D., Knepley, M., McInnes, L.C., Smith, B.F., Zhang, H.: PETSc users manual. Tech. Rep. ANL-95/11 — Revision 2.1.3, Argonne National Laboratory, (2002) See http://www-unix.mcs.anl.gov/petsc/petsc-2/

  3. Balay, S., Gropp, W.D., McInnes, L.C., Smith, B.F.: Efficient management of parallelism in object oriented numerical software libraries. In: Arge, E., Bruaset, A.M., Langtangen, H.P. (eds.) Modern Software Tools in Scientific Computing pp. 163–202. Birkhauser Press, Cambridge, MA (1997)

    Google Scholar 

  4. Balsara, D.S.: Divergence-free adaptive mesh refinement for magnetohydrodynamics. J. Comput. Phys. 174, 614–648 (2001)

    Article  Google Scholar 

  5. Bank, R.E.: PLTMG: A software package for solving elliptic partial differential equations Users Guide 9.0, tech. rep., Department of Mathematics, University of California San Diego (2004)

  6. Bastian, P., Birken, K., Johannsen, K., Lang, S., Neuß, N., Rentz-Reichert, H., Wieners, C.: UG–A flexible software toolbox for solving partial differential equations. Comput. Visual. Sci. 1, 27–40 (1997)

    Article  Google Scholar 

  7. Berger, M.J., Colella, P.: Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys. 82, 64–84 (1989)

    Article  Google Scholar 

  8. Berger, M.J., Oliger, J.: Adaptive mesh refinement for hyperbolic partial differential equations. J. Comput. Phys. 53, 484–512 (1984)

    Article  Google Scholar 

  9. Brown, P.N., Saad, Y.: Hybrid Krylov methods for nonlinear systems of equations. SIAM J. Sci. Statist. Comput. 11, 450–481 (1990)

    Article  Google Scholar 

  10. Buschelman, K.R., Gropp, W.D., McInnes, L.C., Smith, B.F.: PETSc and Overture: Lessons learned developing an interface between components. In: Boisvert, R.F., Tang, P.T.P. (eds.) The Architecture of Scientific Software. Kluwer Boston (2001)

    Google Scholar 

  11. Chacon, L., Knoll, D.A., Finn, J.M.: An implicit, nonlinear reduced resistive MHD solver. J. Comput. Phys. 178, 15–36 (2002)

    Article  Google Scholar 

  12. de Zeeuw, D.L., Gombosi, T.L., Groth, C.P.T., Powell, K.G., Stout, Q.F.: An adaptive MHD method for global space weather simulations. IEEE Trans. Plasma Sci. 28, 1956–1965 (2000)

    Article  Google Scholar 

  13. de Zeeuw, P.M.: Matrix dependent prolongations and restrictions in a black box multigrid solver. J. Comput. Appl. Math. 3, 1–27 (1990)

    Article  Google Scholar 

  14. Dembo, R.S., Eisenstat, S.C., Steihaug, T.: Inexact Newton methods. SIAM J. Numer. Anal. 19, 400–408 (1982)

    Article  Google Scholar 

  15. Dendy, Jr., J.E.: Black box multigrid. J. Comput. Phys. 48, 366–386 (1982)

    Article  Google Scholar 

  16. Dorr, M.R., Garaizar, F.X., Hittinger, J.A.F.: Simulation of laser plasma filamentation using adaptive mesh refinement. J. Comput. Phys. 177, 233–263 (2002)

    Article  Google Scholar 

  17. Eisenstat, S.C., Walker, H.F.: Globally convergent inexact Newton methods. SIAM J. Optimization 4, 393–422 (1994)

    Article  Google Scholar 

  18. Eisenstat, S.C., Walker, H.F.: Choosing the forcing terms in an inexact Newton method. SIAM J. Sci. Comput. 17, 16–32 (1996)

    Article  Google Scholar 

  19. Ewing, R.E., Lazarov, R.D., Vassilevski, P.S.: Local refinement techniques for elliptic problems on cell–centered grids. I: Error analysis. Math. Comp. 56, 437–461 (1991)

    Google Scholar 

  20. Falgout, R.D., Yang, U.M.: Hypre a library of high performance preconditioners. In: Sloot, P.M.A., Tan, C.J.K., Dongarra, J.J., Hoekstra, A.G. (eds.) Computational Science - CARS 2002 Part III, vol. 2331 of Lecture Notes in Computer Science pp. 632–641. New York. Springer-Verlag (2002) See http://www.llnl.gov/CASC/hypre/

  21. Freund, R.W., Golub, G.H., Nachtigal, N.M.: Iterative Solution of Linear Systems. Acta Numerica, pp. 87–100 (1992)

  22. Friedel, H., Grauer, R., Marliani, C.: Adaptive mesh refinement for singular current sheets in incompressible magnetohydrodynamics flow. J. Comput. Phys. 134, 190–198 (1997)

    Article  Google Scholar 

  23. Fuchs, L.: A local mesh refinement technique for incompressible flows. Computers and Fluids 14, 69–81 (1986)

    Article  Google Scholar 

  24. Gamma, E., Helm, R., Johnson, R., Vlissides, J.: Design Patterns: Elements of Reusable Object-Oriented Software. Addison-Wesley, Reading, MA (1995)

    Google Scholar 

  25. Garaizar, X.F., Trangenstein, J.: Adaptive mesh refinement and front-tracking for shear bands in an antiplane shear model. SIAM J. Sci. Comput. 20, 750–779 (1998)

    Article  Google Scholar 

  26. Hairer, E., Wanner, G.: Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems. vol. 14 of Springer Series in Computational Mathematics. Springer-Verlag, Berlin (1991)

    Google Scholar 

  27. Hindmarsh, A.C.: SUNDIALS SUite of Nonlinear and DIfferential/ALgebraic equation Solvers. See http://www.llnl.gov/CASC/sundials/(in press)

  28. Hindmarsh, A.C., Taylor, A.G.: PVODE and KINSOL: Parallel software for differential and nonlinear systems. Tech. Rep. UCRL–ID–129739, Lawrence Livermore National Laboratory (1998)

  29. Hornung, R.D., Kohn, S.: Managing application complexity in the SAMRAI object-oriented framework. Concurrency Comput.: Pract. Exp. 14, 347–368 (2002). See http://www.llnl.gov/CASC/SAMRAI/

    Article  Google Scholar 

  30. Hornung, R.D., Trangenstein, J.A.: Adaptive mesh refinement and multilevel iteration for flow in porous media. J. Comput. Phys. 136, 522–545 (1997)

    Article  Google Scholar 

  31. Knoll, D.A., Chacón, L., Margolin, L.G., Mousseau, V.A.: On balanced approximations for time integration of multiple time scale systems. J. Comput. Phys. 185, 583–611 (2003)

    Article  Google Scholar 

  32. Knoll, D.A., Keyes, D.E.: Jacobian-free Newton-Krylov methods: a survey of approaches and applications. J. Comput. Phys. 193, 357–397 (2004)

    Article  Google Scholar 

  33. Knoll, D.A., Rider, W.J., Olson, G.L.: Nonlinear convergence, accuracy, and time step control in nonequilibrium radiation diffusion. J. Quant. Spectrosc. Ra. 70, 25–36 (2001)

    Article  Google Scholar 

  34. Martin, D.F., Colella, P.: A cell-centered adaptive projection method for the incompressible Euler equations. J. Comput. Phys. 163, 271–312 (2000)

    Article  Google Scholar 

  35. McCormick, S.F.: Multilevel Adpative Methods for Partial Differential Equations. SIAM, Philadelphia, PA (1989)

    Google Scholar 

  36. Mousseau, V.A., Knoll, D.A., Reisner, J.M.: An implicit nonlinearly consistent method for the two-dimensional shallow-water equation with Coriolis force. Mon. Weather Rev. 130, 2611–2625 (2002)

    Article  Google Scholar 

  37. Ober, C.C., Shadid, J.N.: Studies on the accuracy of time integration methods for the radiation diffusion equations. J. Comput. Phys. 195, 743–772 (2004)

    Article  MathSciNet  Google Scholar 

  38. Saad, Y., Schultz, M.H.: GMRES: A generalized minimum residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Statist. Comput. 7, 856–869 (1986)

    Article  Google Scholar 

  39. Schmidt, A., Siebert, K.G.: ALBERT – software for scientific computations and applications. Acta Math. Univ. Comenianae 70, 105–122 (2001)

    Google Scholar 

  40. Taylor, A.G., Hindmarsh, A.C.: User documentation for KINSOL, a nonlinear solver for sequential and parallel computers. Tech. Rep. UCRL–ID–131185, Lawrence Livermore National Laboratory (1998)

  41. Trangenstein, J.A.: Adaptive mesh refinement for wave propagation in nonlinear solids. SIAM J. Sci. Comput. 82, 94–121 (1989)

    Google Scholar 

  42. Wissink, A., Hysom, D., Hornung, R.: Enhancing scalability of parallel structured AMR calculations. In: Proceedings of the 17th ACM International Conference on Supercomputing (ICS03), pp. 336–347. San Francisco, CA (2003)

Download references

Author information

Authors and Affiliations

  1. Computer and Computational Sciences Division, Los Alamos National Laboratory, Los Alamos, NM, 87545, USA

    M. Pernice

  2. Center for Applied Scientific Computing, Lawrence Livermore National Laboratory, Livermore, CA, 94551, USA

    R. D. Hornung

Authors
  1. M. Pernice
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. D. Hornung
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Pernice.

Additional information

Communicated by: G. Wittum

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pernice, M., Hornung, R.D. Newton-Krylov-FAC methods for problems discretized on locally refined grids. Comput. Visual Sci. 8, 107–118 (2005). https://doi.org/10.1007/s00791-005-0156-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00791-005-0156-5

Keywords

Search

Navigation