Algebraic factorizations for 3D non-hydrostatic free surface flows

Abstract.

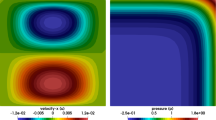
The high amount of computer resources required to simulate complex free surface flows has prompted for developing fractional step schemes capable of reducing the computational effort. These schemes are borrowed from a wider family of methods originally devised for the incompressible Navier–Stokes equations. An alternative approach is to perform an algebraic splitting on the coefficient matrix of the linear system resulting from the discretized problem, ending up with the successive solution of sub-problems of smaller size. The resulting schemes are shown in different cases to be the algebraic counterpart of the standard fractional step formulations. This algebraic procedure was again originally devised in the context of incompressible Navier–Stokes system, but we believe it is far more general: in this paper it is indeed extended to the more involved 3D free surface flow model. The inexact block factorization technique is applied to the coefficient matrix arising from the problem at hand and two significant choices for the approximation are discussed and numerically tested.