Abstract
Exploratory search paradigm assists users who do not have a clear search intent and are unfamiliar with the underlying data space. Query formulation evolves iteratively in this paradigm as a user becomes more familiar with the content. Although exploratory search has received significant attention recently in the context of structured data, scant attention has been paid for graph-structured data. An early effort for building exploratory subgraph search framework on graph databases suffers from efficiency and scalability problems. In this paper, we present a visual exploratory subgraph search framework called ferrari, which embodies two novel index structures called vaccine and advise, to address these limitations. vaccine is an offline, feature-based index that stores rich information related to frequent and infrequent subgraphs in the underlying graph database, and how they can be transformed from one subgraph to another during visual query formulation. advise, on the other hand, is an adaptive, compact, on-the-fly index instantiated during iterative visual formulation/reformulation of a subgraph query for exploratory search and records relevant information to efficiently support its repeated evaluation. Extensive experiments and user study on real-world datasets demonstrate superiority of ferrari to a state-of-the-art visual exploratory subgraph search technique.
















Similar content being viewed by others
Notes
The central ideas in direct manipulation interfaces are visibility of the objects and actions of interest; rapid, reversible, incremental actions; and replacement of typed commands by a pointing action on the object of interest [31].
An overview of this work appeared in [36] as a short 4-page paper.
We can easily extend it to handle deletion of a set of edges (e.g., template pattern) by iteratively updating \(I_L\).
Let a graph g is represented by an adjacency matrix M. Every diagonal entry of M is filled with the label of the corresponding node and every off diagonal entry is filled with 1 or 0 if there is no edge. The cam code is formed by concatenating lower triangular entries of M, including the entries on the diagonal. The order is from top to bottom and from the leftmost entry to the rightmost entry. We choose the maximal code among all possible codes of a graph by lexicographic order as this graph’s canonical code.
Intuitively, canonical labeling is a process in which a graph is relabeled in such a way that isomorphic graphs are identical after relabeling. Hence, isomorphism testing on two graphs can be performed by simply comparing their canonical labeling.
Update of an edge can be considered as deletion followed by addition of a new edge (i.e., modify and add actions).
References
Ahn, J., Brusilovsky, P.: Adaptive visualization for exploratory information retrieval. Inf. Process. Manag. 49(5), 1139–1164 (2013)
Bhowmick, S.S., Chua, H.-E., Choi, B., Dyreson, C.: ViSual: simulation of visual subgraph query formulation to enable automated performance benchmarking. IEEE Trans. Knowl. Data Eng. 29(8), 1765–1778 (2017)
Bonifati, A., Martens, W., Timm, T.: An analytical study of large SPARQL query logs. PVLDB 11(2), 149–161 (2017)
Bonnici, V., Ferro, A., et al.: Enhancing graph database indexing by suffix tree structure. In: Pattern Recognition in Bioinformatics (2010)
Cordella, L., Foggia, P., Sansone, C., Vento, M.: A (sub)graph isomorphism algorithm for matching large graphs. IEEE Trans. PAMI 26(10), 1367–1372 (2004)
Demetrescu, C., Eppstein, D., Galil, Z., Italiano. G.F.: Dynamic graph algorithms. In: Algorithms and Theory of Computation Handbook. CRC Press, Boca Raton (2010)
Di Natale, R., Ferro, A., et al.: Sing: subgraph search in non-homogeneous graphs. BMC Bioinform. 11(1), 96 (2010)
Elseidy, M., Abdelhamid, E., et al.: GRAMI: frequent subgraph and pattern mining in a single large graph. Proc. VLDB Endow. 7(7), 517–528 (2014)
Fan, W., Hu, C., Tian, C.: Incremental graph computations: doable and undoable. In SIGMOD (2017)
Fan, W., Wang, X., Wu, Y.: Incremental graph pattern matching. ACM Trans. Database Syst. 38(3), 1–47 (2013)
Galakatos, A., Crotty, A., et al.: Revisiting reuse for approximate query processing. Proc. VLDB Endow. 10(10), 1142–1153 (2017)
Huan, J.P., Wang, W., Prins, J.: Efficient mining of frequent subgraph in the presence of isomorphism. In ICDM (2003)
Huang, K., Bhowmick, S.S., Zhou, S., Choi, B.: PICASSO: exploratory search of connected subgraph substructures in graph databases. Proc. VLDB Endow. 10(12), 1861–1864 (2017)
Hung, H.H., Bhowmick, S.S., Truong, B.Q., Choi, B., Zhou, S.: QUBLE: towards blending interactive visual subgraph search queries on large networks. VLDB J. 23(3), 401–426 (2014)
Idreos, S., Papaemmanouil, O., Chaudhuri, S.: Overview of data exploration techniques. In SIGMOD (2015)
Jayaram, N., Goyal, S., Li, C.: VIIQ: auto-suggestion enabled visual interface for interactive graph query formulation. Proc. VLDB Endow. 8(12), 1940–1943 (2015)
Jayachandran, P., Tunga, K., Kamat, N., Nandi, A.: Combining user interaction, speculative query execution and sampling in the DICE system. Proc. VLDB Endow. 7(13), 1697–1700 (2014)
Jin, C., Bhowmick, S.S., Choi, B., Zhou, S.: PRAGUE: a practical framework for blending visual subgraph query formulation and query processing. In ICDE (2012)
Jin, C., Bhowmick, S.S., Xiao, X., Cheng, J., Choi, B.; Gblender: towards blending visual query formulation and query processing in graph databases. In ACM SIGMOD (2010)
Katsarou, F., Ntarmos, N., Triantafillou, P.: Performance and scalability of indexed subgraph query processing methods. Proc. VLDB Endow. 8(12), 1566–1577 (2015)
Kim, S., et al.: PubChem Substance and Compound Databases. Nucleic Acids Research, 44(D1). Oxford University Press, Oxford (2015)
Koutrika, G., et al.: Exploratory search in databases and the web. In EDBT Workshop (2014)
Laura Faulkner, L.: Beyond the five-user assumption: benefits of increased sample sizes in usability testing. Behav. Res. Methods Instrum. Comput. 35(3), 379–383 (2003)
Lazar, J., Feng, J.H., Hochheiser, H.: Research Methods in Human–Computer Interaction. Wiley, Hoboken (2010)
Marchionini, G.: Exploratory search: from finding to understanding. Commun. ACM 49(4), 41–46 (2006)
McKay, B.D., Piperno, A.: Practical graph isomorphism, II. J. Symb. Comput. 60, 94–112 (2014)
Mongiova, M., Natale, R.D., Giugno, R., Pulvirenti, A., Ferro, A.: Sigma: a set-cover-based inexact graph matching algorithm. J. Bioinform. Comput. Biol. 80, 199–218 (2010)
Namaki, M.H., Wu, Y., Zhang, X.: GExp: cost-aware graph exploration with keywords. In SIGMOD (2018)
Pienta, R., Hohman, F., et al.: Visual graph query construction and refinement. In SIGMOD (2017)
Sarrafzadeh, B., Lank, E.: Improving exploratory search experience through hierarchical knowledge graphs. In SIGIR (2017)
Shneiderman, B., Plaisant, C., Cohen, M., Jacobs, S.: Designing the User Interface: Strategies for Effective Human–Computer Interaction, 5th edn. Pearson, London (2009)
Shang, H., et al.: Connected substructure similarity search. In SIGMOD (2010)
Siddiqui, T., et al.: Effortless data exploration with zenvisage: an expressive and interactive visual analytics system. PVLDB 10(4), 457–468 (2016)
Song, Y., Chua, H.E., Bhowmick, S.S., Choi, B., Zhou, S.: BOOMER: blending visual formulation and processing of p-homomorphic queries on large networks. In SIGMOD (2018)
Sun, S., Luo, Q.: Scaling up subgraph query processing with efficient subgraph matching. In ICDE (2019)
Wang, C., Xie, M., Bhowmick, S.S., Choi, B., Xiao, X., Zhou, S.: An indexing framework for efficient visual exploratory subgraph search in graph databases. In ICDE (2019)
White, R.W., Roth, R.A.: Exploratory Search: Beyond the Query-response Paradigm. Synthesis Lectures on Information Concepts, Retrieval, and Services, vol. 1, 1 (2009)
Yahya, M., Berberich, K., et al.: Exploratory querying of extended knowledge graphs. Proc. VLDB Endow. 9(13), 1521–1524 (2016)
Yan, X., Han, J.: gspan: graph-based substructure pattern mining. In ICDM (2002)
Yan, X., Yu, P.S., Han, J.: Graph indexing: a frequent structure-based approach. In SIGMOD (2004)
Yan, X., Yu, P.S., Han, J.: Substructure similarity search in graph databases. In ACM SIGMOD (2005)
Yi, P., Choi, B., et al.: AutoG: a visual query autocompletion framework for graph databases. VLDB J. 26(3), 347–372 (2017)
Acknowledgements
The first three authors are supported by AcRF MOE2015-T2-1-040 and AcRF Tier-1 Grant RG24/12. Shuigeng Zhou is supported by National NSF of China (Grant No. U1636205).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Proofs
Proof of Lemma 1(Sketch). Algorithm 2 builds a vaccine index by adding all frequent fragments one by one and connecting them together by their transformation relationships via two types of primitive transformers. So the number of vertices in a vaccine index is the total number of frequent fragments and difs (i.e., N). For a frequent fragment f, there are at most \(N_{fmax}\) nodes. Hence, we can add \(C_{N_{fmax}}^2\) new edges for connecting current nodes in f. In addition, there are at most \(N_{fe}\) different ways to add a new frequent edge of a new labeled node to a current node in f. So it can create at most \(N_{fmax}N_{fe}\) edges. Thus, there are \(O(N(C_{N_{fmax}}^{2}+N_{fmax}N_{fe}))\) edges at most in a vaccine index.
Proof of Theorem 1(Sketch). In Algorithm 2, the process for creating vaccine index can be divided into three major steps. The first step (Line 1) is to mine all frequent fragment from \(\mathcal {D}\), whose time complexity is denoted as \(C_{ff}\). The second step (Line 5–10) is to fetch all frequent edges in \(\mathcal {D}\) and store them in a matrix. Its time complexity is O(|E|). The third step (Line 11–14) is to iterate through all frequent fragments to create the index by utilizing the node and edge transformers. Assume the time complexity of the canonical labeling process is \(C_{cl}\). Then the time complexities of node and edge transformers are \(O(N_{fmax}|\mathcal {L}|C_{cl})\) and \(N_{fmax}^{2}C_{cl})\), respectively. Hence the overall complexity is \(N_{f}C_{cl}(N_{fmax}|\mathcal {L}|+N_{fmax}^{2})\). The final step (Line 15–17) is to compute data graph identifier set of difs. Its complexity is \(O(N_{dif}N_{dmax})\). Thus, the time complexity for building vaccine index is \(O(C_{ff} + |\mathcal {E}|+N_{f}C_{cl}(N_{fmax}|\mathcal {L}|+N_{fmax}^{2}) + N_{dif}N_{dmax})\).
Proof of Theorem 2(Sketch). First, we prove the following lemma, which we shall be using subsequently.
Lemma 2
Given a vaccine index \(G_{I}=(V_{I}, E_{I})\), the time complexity of processing a new edge \(e_{\ell }\) to the current query fragment \(q=(V_{q},E_{q})\) is \(O(|V_{I}|C_{CAM} + min(|V_{I}|, x_{f})(|V_{q}| + |E_{q}|))\), where \(x_{f}\) is the number of frequent fragments and DIFs of q in \(G_{I}\) that contains \(e_{\ell }\) and \(C_{CAM}\) is the time complexity of comparing the cam codes of a pair of graphs.
Proof of Lemma 2
When a new edge \(e_\ell \) is added to the current query fragment q, Algorithm 4 first compares the cam code of \(e_\ell \) with all fragments in \(G_{I}\) to check whether the new edge is a frequent fragment or a dif. If it is, then we can get the corresponding matching vertex for \(e_\ell \) (Line 1). The time complexity for this task is \(O(|V_{I}|C_{CAM})\). Next, the algorithm finds and indexes all frequent fragments and difs that contain \(e_\ell \) gradually by utilizing the primitive transformers associated with the edges of the matching vertex. For each fragment, it performs three tasks: (a) compare the transformer information with all children of the matching vertex for finding the next one via MatchingInVaccine function (Line 11), (b) update/add vertex for matched fragments (Lines 12–15) and its parental relationships (Lines 16), and (c) push itself to the queue (Line 17). The time complexities of these three tasks are O(1) (using a suitable hash function), \(O(|V_{q}| +|E_{q}|)\) (there are at most \(|E_{q}|-1\) parent-child relationships in \(G_{I}\) for a fragment) and O(1), respectively. The upper bound of the number of frequent fragments and difs is the minimum value of \(|V_{I}|\) and \(x_{f}\). Thus, the complexity of processing each new edge during query formulation is \(O(|V_{I}|C_{CAM} + min(|V_{I}|, x_{f}) (|V_{q}| + |E_{q}|))\). \(\square \)
Proof of Theorem 2
From Lemma 2, we know that the time complexity for building advise index by adding an edge \(e_{\ell }\) to the current query graph \(q_{c}=(V_{q_{c}}, E_{q_{c}})\) is \(O(|V_{I}|C_{CAM} + min(|V_{I}|, x_{f})(|V_{q_{c}}| + |E_{q_{c}}|))\) where \(x_{f}\) is the number of frequent fragments and difs of \(q_{c}\) in \(G_{I}\) that contains \(e_{\ell }\). The whole query q is formulated gradually, thus \(|E_{q_{c}}| \le |E_{q}|\) and \(|V_{q_{c}}| \le |V_{q}|\). So the worst-case cost for adding a query edge is \(O(|V_{I}|C_{CAM} + min(|V_{I}|, x_{fq})(|V_{q}| + |E_{q}|))\). Because there are at most \(E_{q}\) different edges with distinct labels to be added during the formulation of q, the total time complexity is \(O(|E_{q}|*(|V_{I}|C_{CAM} + min(|V_{I}|, x_{fq}) (|V_{q}| + |E_{q}|)))\). \(\square \)
The upper bound of the number of vertices in \(G_{A}\) is the minimum value of \((|V_{I}|\) and \(2^{|E_{q}|}-1)\). Thus, the space complexity of advise index is \(m*min(|V_{I}|, 2^{|E_{q}|}-1)\).
GUI of FERRARI and PICASSO
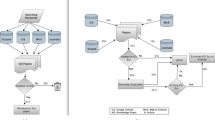
Figure 17 depicts the direct manipulation interface of picasso and ferrari. It consists of the following panels.
-
An Attribute Panel (Panel 2) to display a set of labels or attributes of nodes or edges of the underlying data.
-
A Pattern Panel (Panel 3) to display a set of template patterns that can aid query formulation.
-
A Query Panel (Panel 4) for constructing a graph query graphically by leveraging the Attribute and Pattern Panels.
-
A Results Exploration Panel (Panel 5) that displays the query results during exploration.
A typical query would be constructed using the interface by performing the following sequence of steps.
-
1.
Move the mouse cursor to the Attribute or Pattern Panel.
-
2.
Scan and select a label or pattern (e.g., label C, benzene ring pattern).
-
3.
Drag the selected item to the Query Panel and drop it. Each such action represents formulation of a single node or a query fragment in the query graph.
-
4.
Repeat, if necessary, Steps 1–3 for constructing another node or a query fragment.
-
5.
Construct edges (if necessary) between relevant nodes in the constructed subgraphs by clicking on them.
-
6.
Repeat Steps 4 and 5 until the query graph is executed by clicking on the Run icon.
Rights and permissions
About this article
Cite this article
Wang, C., Xie, M., Bhowmick, S.S. et al. FERRARI: an efficient framework for visual exploratory subgraph search in graph databases. The VLDB Journal 29, 973–998 (2020). https://doi.org/10.1007/s00778-020-00601-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00778-020-00601-0