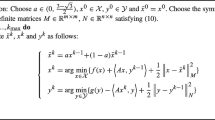Abstract
Signal reconstruction problem (SRP) is an important optimization problem where the objective is to identify a solution to an underdetermined system of linear equations that is closest to a given prior. It has a substantial number of applications in diverse areas including network traffic engineering, medical image reconstruction, acoustics, astronomy and many more. Most common approaches for SRP do not scale to large problem sizes. In this paper, we propose multiple optimization steps, developing scalable algorithms for the problem. We first propose a dual formulation of the problem and develop the Direct algorithm that is significantly more efficient than the state of the art. Second, we show how adapting database techniques developed for scalable similarity joins provides a significant speedup over Direct, scaling our proposal up to large-scale settings. Third, we describe a number of practical techniques that allow our algorithm to scale to settings of size in the order of a million by a billion. We also adapt our proposal to identify the top-k components of the solved system of linear equations. Finally, we consider the dynamic setting where the inputs to the linear system change and propose efficient algorithms inspired by the database techniques of materialization and reuse. Extensive experiments on real-world and synthetic data confirm the efficiency, effectiveness and scalability of our proposal.



































Similar content being viewed by others
Notes
We assume that the problem has at least one solution.
Note that \(\min \frac{1}{2}X^\mathrm{T}X - {X'}^\mathrm{T}X\) is the same as \(\min ||X-X'||_2\).
We have found out the knee point of the cumulative flow is around 2%.
References
Beyer, K., Gemulla, R., Haas, P.J., Reinwald, B., Sismanis, Y.: Distinct-value synopses for multiset operations. Commun. ACM 52(10), 87–95 (2009)
Bjerhammar, A.: Application of Calculus of Matrices to Method of Least Squares: With Special Reference to Geodetic Calculations. Elander, Göteborg (1951)
Boehm, M., Dusenberry, M.W., Eriksson, D., Evfimievski, A.V., Manshadi, F.M., Pansare, N., Reinwald, B., Reiss, F.R., Sen, P., Surve, A.C., et al.: SystemML: declarative machine learning on spark. PVLDB 9(13), 1425–1436 (2016)
Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)
Broder, A.Z.: On the resemblance and containment of documents. In: Proceedings on Compression and Complexity of Sequences 1997, pp. 21–29 (1997)
Candes, E.J., Romberg, J.K., Tao, T.: Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 59(8), 1207–1223 (2006)
Cao, J., Davis, D., Vander Wiel, S., Yu, B.: Time-varying network tomography: router link data. J. Am. Stat. Assoc. 95(452), 1063–1075 (2000)
Chandrasekaran, B.: Survey of Network Traffic Models, vol. 567. Washington University, St. Louis CSE (2009)
Chaudhuri, S., Ganti, V., Kaushik, R.: A primitive operator for similarity joins in data cleaning. In: ICDE (2006)
Cohen, E., Kaplan, H.: Tighter estimation using bottom k sketches. PVLDB 1(1), 213–224 (2008)
Cormode, G., Korn, F., Muthukrishnan, S., Srivastava, D.: Finding hierarchical heavy hitters in data streams. In: Proceedings of the 29th International Conference on Very Large Data Bases, vol. 29, pp. 464–475. VLDB Endowment (2003)
Craig, I.J., Brown, J.C.: Inverse problems in astronomy: a guide to inversion strategies for remotely sensed data. In: Research Supported by SERC. Adam Hilger, Ltd., Bristol and Boston (1986)
Dasu, T., Johnson, T., Muthukrishnan, S., Shkapenyuk, V.: Mining database structure; or, how to build a data quality browser. In: Proceedings of the 2002 ACM SIGMOD International Conference on Management of Data, pp. 240–251. ACM (2002)
Ding, B., König, A.C.: Fast set intersection in memory. PVLDB 4(4), 255–266 (2011)
Dokmanić, I., Gribonval, R.: Beyond Moore–Penrose part II: the sparse pseudoinverse (2017). arXiv:1706.08701
Erdos, P., Rényi, A.: On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 5(1), 17–60 (1960)
Fortz, B., Thorup, M.: Optimizing OSPF/IS-IS weights in a changing world. IEEE J. Sel. Areas Commun. 20(4), 756–767 (2002)
Ge, D., Jiang, X., Ye, Y.: A note on the complexity of \(L_p\) minimization. Math. Program. 129(2), 285–299 (2011)
Goldschmidt, O.: ISP backbone traffic inference methods to support traffic engineering. In: Internet Statistics and Metrics Analysis (ISMA) Workshop, pp. 1063–1075 (2000)
Gong, Y.: Identifying P2P users using traffic analysis (2005). www.symantec.com/connect/articles/identifying-p2p-users-using-traffic-analysis. Accessed 21 May 2007
Gordon, J.: Pareto process as a model of self-similar packet traffic. In: Global Telecommunications Conference, 1995 (GLOBECOM’95) vol. 3, pp. 2232–2236 (1995)
Grangeat, P., Amans, J.L.: Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine, vol. 4. Springer, Berlin (2013)
Hadjieleftheriou, M., Yu, X., Koudas, N., Srivastava, D.: Hashed samples: selectivity estimators for set similarity selection queries. PVLDB 1(1), 201–212 (2008)
Hansen, P.C.: Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion. SIAM, Philadelphia (1998)
Hasani, S., Thirumuruganathan, S., Asudeh, A., Koudas, N., Das, G.: Efficient construction of approximate ad-hoc ML models through materialization and reuse. Proc. VLDB Endow. 11(11), 1468–1481 (2018)
Hrinivich, W.T., Hoover, D.A., Surry, K., Edirisinghe, C., D’Souza, D., Fenster, A., Wong, E.: Ultrasound guided high-dose-rate prostate brachytherapy: live needle segmentation and 3d image reconstruction using the sagittal transducer. Brachytherapy 15, S195 (2016)
Kaoudi, Z., Quiané-Ruiz, J.A., Thirumuruganathan, S., Chawla, S., Agrawal, D.: A cost-based optimizer for gradient descent optimization. In: Proceedings of the 2017 ACM International Conference on Management of Data, pp. 977–992. ACM (2017)
Kim, Y., Nelson, P.: Optimal regularisation for acoustic source reconstruction by inverse methods. J. Sound Vib. 275(3), 463–487 (2004)
Kleinrock, L., Kamoun, F.: Hierarchical routing for large networks performance evaluation and optimization. Comput. Netw. 1(3), 155–174 (1977)
Kumar, A., Naughton, J., Patel, J.M., Zhu, X.: To join or not to join? Thinking twice about joins before feature selection. In: Proceedings of the 2016 International Conference on Management of Data, pp. 19–34. ACM (2016)
Lagrange, J.L.: Mécanique Analytique, vol. 1. Mallet-Bachelier, Paris (1853)
Leskovec, J., Faloutsos, C.: Sampling from large graphs. In: Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 631–636. ACM (2006)
Leskovec, J., Kleinberg, J., Faloutsos, C.: Graphs over time: densification laws, shrinking diameters and possible explanations. In: Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, pp. 177–187. ACM (2005)
McMahan, B., Ramage, D.: Federated learning: collaborative machine learning without centralized training data. Technical report, Google (2017)
Medina, A., Taft, N., Salamatian, K., Bhattacharyya, S., Diot, C.: Traffic matrix estimation: existing techniques and new directions. ACM SIGCOMM Comput. Commun. Rev. 32(4), 161–174 (2002)
Moors, E.: On the reciprocal of the general algebraic matrix (abstract). Bull. Am. Math. Soc. 26, 394–395 (1920)
Needell, D., Tropp, J.A.: CoSaMP: iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 26(3), 301–321 (2009)
Nunes, B.A.A., Mendonca, M., Nguyen, X.N., Obraczka, K., Turletti, T.: A survey of software-defined networking: past, present, and future of programmable networks. IEEE Commun. Surv. Tutor. 16(3), 1617–1634 (2014)
Penrose, R.: A generalized inverse for matrices. In: Mathematical proceedings of the Cambridge philosophical society, vol. 51, pp. 406–413. Cambridge University Press, Cambridge (1955)
Tebaldi, C., West, M.: Bayesian inference on network traffic using link count data. J. Am. Stat. Assoc. 93(442), 557–573 (1998)
Trefethen, L.N., Bau III, D.: Numerical linear algebra. Society for Industrial and Applied Mathematics, Philadelphia. Technical report, ISBN 978-0-89871-361-9 (1997)
Tsirogiannis, D., Guha, S., Koudas, N.: Improving the performance of list intersection. PVLDB 2(1), 838–849 (2009)
Tune, P., Roughan, M.: Maximum entropy traffic matrix synthesis. In: ACM SIGMETRICS Performance Evaluation Review vol. 42(2), pp. 43–45 (2014)
Vogel, C.R.: Computational Methods for Inverse Problems. SIAM, Philadelphia (2002)
Zhang, C., Kumar, A., Ré, C.: Materialization optimizations for feature selection workloads. ACM Trans. Datab. Syst. (TODS) 41(1), 2 (2016)
Zhang, Y., Roughan, M., Duffield, N., Greenberg, A.: Fast accurate computation of large-scale IP traffic matrices from link loads. In: ACM SIGMETRICS Performance Evaluation Review, vol. 31, pp. 206–217. ACM (2003)
Zhang, Y., Roughan, M., Lund, C., Donoho, D.: An information-theoretic approach to traffic matrix estimation. In: Proceedings of the 2003 conference on Applications, technologies, architectures, and protocols for computer communications, pp. 301–312. ACM (2003)
Funding
This paper was supported in part by AT&T and National Science Foundation (Grant No. 1343976, 1443858, 1624074, and 1760059).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
Theoretical negative result for sparsity of \(AA^\mathrm{T}\)
In this section, we study an adversarial case that shows the negative result that in theory \(t=AA^\mathrm{T}\) can be non-sparse and even thresholding will not significantly help to make them sparse.
We found the negative result in the context of traffic matrix reconstruction. We use the chain graph (Fig. 36), while considering all pairs of nodes as valid SD pairs, as an adversarial case in this section. This provides the upper bound on the number of nonzero elements in \(t=AA^\mathrm{T}\):
Theorem 4
\(n^2\) is the tight upper bound on the number of nonzero elements in \(t=AA^\mathrm{T}\) for SRP.
Proof
We use the chain graph for proving the upper bound. As we discussed in Sect. 5.2, each cell t[i, j] is the number of SD pairs that contain both edges \(e_i\) and \(e_j\) in their route. In following, we show that every pair of edges in the chain share at least one flow. Note that in the chain, there is a unique path between each pair of nodes, containing the set of edges between the two nodes. Consider the first and last nodes in the chain, i.e., \(N_1\) and \(N_{r}\) in Fig. 36. The path between these two nodes contains \(\{e_1,e_2, \cdots , e_{r-1}\}\), i.e., all edges of the graph. It means for any pair \(e_i\) and \(e_j\), there exists at least one SD pair that contains both of them in their path. As a result, for the case of chain, all cells of matrix t are nonzero. The existence of a case for which none of the elements in \(t=AA^\mathrm{T}\) are zero provides the tight upper bound on the nonzero elements of t as \(n^2\).\(\square \)
The problem in the chain is that the choice of paths between the SD pairs is very limited and all traffic should flow within the same paths. Fortunately, in practice, having a graph structure, there are multiple alternatives for paths, reducing the chance that two random edges share at least a flow. In our experiments in Sect. 7, the number of nonzero values was always below 2% of \(AA^\mathrm{T}\) cells.
Next, we show that even thresholding cannot help, increasing the sparsity in the chain. For simplicity of explanations, let the indexing of nodes and edges be as presented in Fig. 36. Note that in this graph, there are \(n=r-1\) edges and \(m={r \atopwithdelims ()2}\) SD pairs. The first observation is that there is only one pair of edges (\(e_1\) and \(e_{r-1}\)) that only share one flow between them. That is, only the cells \(t[1,r-1]\) and \(t[r-1,1]\) have the value of 1, and all other cells have larger values. It means with the threshold of \(\tau =2\), there are only two cells with values less than \(\tau \) in \(t = AA^\mathrm{T}\).
Now, consider a pair of edges \(e_i\) and \(e_j\) where \(i\le j\). Looking at Fig. 36, there are exactly i nodes in the left-hand side of \(e_i\) and exactly \((r-j)\) nodes in the right-hand side of \(e_j\). Note that only the SD pairs with one of their nodes in the left-hand side of \(e_i\) and the other in the right-hand side of \(e_j\) have both \(e_i\) and \(e_j\) in their paths. There exist \(i(r-j)\) such pairs. Following this, one can calculate the value of t[i, j] as \(t[i,j]=t[j,i] = i(r-j)\). Therefore, the number of cells with values smaller than a threshold \(\tau \) is equal to two times the number of cases of \(i\le j\) such that \(i(r-j)< \tau \). For a fixed value \(i\in [i,\tau )\):
This means, for each such value \(i\in [i,\tau )\), there are \(\frac{\tau -1}{i}\) values of j satisfying the above condition. In other words, for each such value i, there are \(2\frac{\tau -1}{i}\) cells in t with values at least equal to \(\tau \). Using this, the number of cells with nonzero elements in \(t=AA^\mathrm{T}\) is:
where H is the hyperbolic function.
Equation 14 shows the negative result that for a chain, even thresholding will not make \(AA^\mathrm{T}\) sparse. That is because the number of cells with value less that \(\tau \) is independent of the size of \(AA^\mathrm{T}\). As a result, for a large value of r, the number of nonzero elements in \(AA^\mathrm{T}\) almost does not reduce by thresholding.
Rights and permissions
About this article
Cite this article
Asudeh, A., Augustine, J., Nazi, A. et al. Scalable algorithms for signal reconstruction by leveraging similarity joins. The VLDB Journal 29, 681–707 (2020). https://doi.org/10.1007/s00778-019-00562-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00778-019-00562-z