Abstract
Increasing single instruction multiple data (SIMD) capabilities in modern hardware allows for the compilation of data-parallel query pipelines. This means GPU-alike challenges arise: control flow divergence causes the underutilization of vector-processing units. In this paper, we present efficient algorithms for the AVX-512 architecture to address this issue. These algorithms allow for the fine-grained assignment of new tuples to idle SIMD lanes. Furthermore, we present strategies for their integration with compiled query pipelines so that tuples are never evicted from registers. We evaluate our approach with three query types: (i) a table scan query based on TPC-H Query 1, that performs up to 34% faster when addressing underutilization, (ii) a hashjoin query, where we observe up to 25% higher performance, and (iii) an approximate geospatial join query, which shows performance improvements of up to 30%.
Similar content being viewed by others
1 Introduction
Integrating SIMD processing with database systems has been studied for more than a decade [28]. Several operations, such as selection [12, 23], join [2, 3, 10, 26], partitioning [20], sorting [5], CSV parsing [17], regular expression matching [25], and (de-)compression [15, 23, 27] have been accelerated using the SIMD capabilities of the x86 architectures. In more recent iterations of hardware evolution, SIMD instruction sets have become even more popular in the field of database systems. Wider registers, higher degrees of data-parallelism, and comprehensive support for integer data has increased the interest in SIMD and led to the development of many novel algorithms.
SIMD is mostly used in interpreting database systems [9] that use the column-at-a-time or vector-at-a-time execution model [4]. Compiling database systems [9] like HyPer [8] barely use it due to their data-centric tuple-at-a-time execution model [18]. In such systems, therefore, SIMD is primarily used in scan operators [12] and in string processing [17].
With the increasing vector-processing capabilities for database workloads in modern hardware, especially with the advent of the AVX-512 instruction set, query compilers can now vectorize entire query execution pipelines and benefit from the high degree of data-parallelism [6]. With AVX-512, the width of vector registers increased to 512 bit, allowing for the processing of an entire cache line in a single instruction. Depending on the bit-width of the attribute values, data elements from up to 64 tuples can be packed into a single register.
Vectorizing entire query pipelines raises new challenges. One such challenge is keeping all SIMD lanes busy during query evaluation, as not all in-flight tuples follow the same control flow. For instance, some might is disqualified during predicate evaluation, while others may not find a join partner later on and get discarded. Whenever a tuple gets disqualified, the corresponding SIMD lane is affected. A scalar (non-vectorized) pipeline would take a branch and thereby return the control flow to a tuple producing operator to fetch the next tuple. In a vectorized pipeline, this is only possible iff all in-flight tuples have been disqualified. If this is not the case, the query of the subsequent operator still needs to be executed. Ignoring SIMD lanes containing disqualified tuples is the easiest way to deal with this situation, as it does not introduce branching logic and only requires a small amount of bookkeeping. A small bitmap is sufficient to keep track of disqualified elements. The bitmap is used at the pipeline sink, when the (intermediate) result is materialized, making sure that disqualified elements are not written to the query result set. The downside of this approach is, that within the pipeline, all instructions are performed on all SIMD lanes regardless of whether the SIMD lane contains an active or an inactive element. All operations that are performed on inactive elements can be considered overhead, as they do not contribute to the result. In other words, not all SIMD lanes perform useful work and if lanes contain disqualified elements, the vector-processing units (VPUs) can be considered underutilized. Therefore, efficient algorithms are required to counter the underutilization of vector-processing units. In [16], this issue was addressed by introducing (memory) materialization points immediately after each vectorized operator. However, with respect to the more strict definition of pipeline breakers given in [18], materialization points can be considered as pipeline breakers because tuples are evicted from registers to slower (cache) memory. In this work, we present alternative algorithms and strategies that do not break pipelines. Further, our approach can be applied at the intra-operator level as well as at operator boundaries.
The remainder of this paper is organized as follows. In Sect. 2, we briefly describe the relevant AVX-512 instructions that we use in our algorithms. The potential performance degradation caused by underutilization in holistically vectorized pipelines is discussed in Sect. 3. In Sect. 4, we introduce efficient algorithms to counter underutilization, and in Sect. 5, we present strategies for integrating these algorithms with compiled query pipelines. The experimental evaluation of the proposed algorithms using a table scan query, a hashjoin query, and an approximate geospatial join query is given in Sect. 6. The experimental results are summarized and discussed in Sect. 7, followed by our conclusions in Sect. 8.
2 Background
In this section, we briefly describe the key features of the AVX-512 instruction set that we use in our algorithms in Sect. 4. In particular, we cover the basics of vector predication as well as the permute and the compress/expand instructions.
Mask instructions: Almost all AVX-512 instructions support predication. These instructions allow to perform a vector operation only on those vector components (or lanes) specified by a given bitmask, where the \(i{\text {th}}\) bit in the bitmask corresponds to the \(i{\text {th}}\) lane. For example, an
 instruction in its simplest form requires two (vector) operands and a destination register that receives the result. In AVX-512, the instruction exists in two additional variants:
instruction in its simplest form requires two (vector) operands and a destination register that receives the result. In AVX-512, the instruction exists in two additional variants:
- 1.
Merge masking: The instruction takes two additional arguments, a mask and a source register, for example,
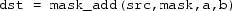 . The addition is performed on the vector components in
. The addition is performed on the vector components in
 and
and
 specified by the
specified by the
 . The remaining elements, where the mask bits are
. The remaining elements, where the mask bits are
 , are copied from
, are copied from
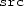 to
to
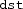 at their corresponding positions.
at their corresponding positions. - 2.
Zero masking: The functionality is basically the same as that of merge masking, but instead of specifying an additional source vector, all elements in
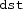 are set to zero if the corresponding bit in the mask is not set. Zero masking is, therefore, (logically) equivalent to merge masking with
are set to zero if the corresponding bit in the mask is not set. Zero masking is, therefore, (logically) equivalent to merge masking with
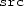 set to zero:
set to zero:
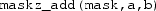 \(\equiv \)
\(\equiv \)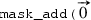
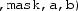 ). Thus, zero masking is a special case of merge masking.
). Thus, zero masking is a special case of merge masking.
Masked instructions can be used to prevent individual vector components from being altered, e.g.,
 .
.
Typically, masks are created using comparison instructions and stored in special mask registers, which is a significant improvement over earlier SIMD instruction sets, in which these masks were stored in 256-bit vector registers.
Permute: The
 instruction shuffles elements within a vector register according to a given index vector:
instruction shuffles elements within a vector register according to a given index vector:
It is noteworthy, that the
 instruction has already been available in earlier instruction sets. But due to the doubled register size, twice as many elements can now be processed at once. Further, in our application, we achieve four times higher throughput compared to the earlier AVX2 instruction set. The reason is, that assigning new elements to idle SIMD lanes is basically a merge operation of the content of two vector registers. In combination with merge masking, this operation can be performed using a single instruction, whereas with AVX2, two instructions need to be issued, (i) a
instruction has already been available in earlier instruction sets. But due to the doubled register size, twice as many elements can now be processed at once. Further, in our application, we achieve four times higher throughput compared to the earlier AVX2 instruction set. The reason is, that assigning new elements to idle SIMD lanes is basically a merge operation of the content of two vector registers. In combination with merge masking, this operation can be performed using a single instruction, whereas with AVX2, two instructions need to be issued, (i) a
 to move the elements into their desired SIMD lanes and (ii) a
to move the elements into their desired SIMD lanes and (ii) a
 to select the desired lanes from two source registers and merge them into a destination register.
to select the desired lanes from two source registers and merge them into a destination register.
Compress/Expand: Typically, before a
 instruction can be issued, an algorithm needs to determine the aforementioned index vector, which used to be a tedious task that often induced significant overheads, such as additional accesses into predefined lookup tables [7, 12, 16, 22]. The key instructions introduced with AVX-512 to efficiently solve these types of problems, are called
instruction can be issued, an algorithm needs to determine the aforementioned index vector, which used to be a tedious task that often induced significant overheads, such as additional accesses into predefined lookup tables [7, 12, 16, 22]. The key instructions introduced with AVX-512 to efficiently solve these types of problems, are called
 and
and
 .
.
 stores the active elements (indicated by a bitmask) contiguously into a target register, and
stores the active elements (indicated by a bitmask) contiguously into a target register, and
 stores the contiguous elements of an input at certain positions (specified by a write mask) in a target register:
stores the contiguous elements of an input at certain positions (specified by a write mask) in a target register:

Both instructions come in two flavors: (i) read/write from/to memory and (ii) directly operate on registers.
Our algorithms in general require both,
 and
and
 instructions. There is only one special case, where a
instructions. There is only one special case, where a
 suffices, which we describe in the later Sect. 4.
suffices, which we describe in the later Sect. 4.
3 Vectorized pipelines
As mentioned in the introduction, the major difference between a scalar (i.e., non-vectorized) pipeline, as pioneered by HyPer [8], and a vectorized pipeline is that in the latter, multiple tuples are pushed through the pipeline at once. This impacts the control flow within the query pipeline. In a scalar pipeline, whenever the control flow reaches any operator, it is guaranteed that there is exactly one tuple to process (tuple-at-a-time). By contrast, in a vectorized pipeline, there are several tuples to process. However, because the control flow is not necessarily the same for all tuples, some SIMD lanes may become inactive when a conditional branch is taken. Such a branch is only taken if at least one element satisfies the branch condition. This implies that a vector of length n may contain up to \(n-1\)inactive elements, as depicted in Fig. 1. The figure shows a simplified control flow graph (CFG) for an example query pipeline that consists of a table scan, a selection, and a join operator. The directed edges represent the branching logic. For instance, the no match edges are taken if a tuple is disqualified in the selection or the join operator. The index traversal (self-)edge is taken when an index lookup is performed. For instance, a hash table or tree lookup might require one to follow multiple bucket pointers until a join partner for the current tuples is found. The right-hand side of Fig. 1 visualizes the SIMD lane utilization over time. Initially, in the scan operator, all SIMD lanes are active (green color). Inside the select or join operator, elements are disqualified (marked with a X), but the no match branch is not taken, because some elements are still active. Lane 4 represents a different situation, where an SIMD lane becomes temporarily inactive. In that example, the element in lane 4 finds its join partner in the very first iteration of the index lookup. However, lanes 1 and 6 need three iterations until the index lookup terminates. During that time, lane 4 is idle and afterward, it becomes active again.
In general, all conditional branches within the query pipeline are potential sources of control flow divergence and, therefore, a source of the underutilization of VPUs, whereas, disqualified elements cause underutilization in all subsequent operators and lookups in index structures cause intra-operator underutilization. The latter is an inherent problem when traversing irregular pointer-based data structures in an SIMD fashion [24]. To avoid underutilization through divergence, we need to dynamically assign new tuples to idle SIMD lanes, possibly at multiple “points of divergence” within the query pipeline. We refer to this process as pipeline refill.
4 Refill algorithms
In this section, we present our refill algorithms for AVX-512, which we later integrate into compiled query pipelines (cf., Sect. 5). These algorithms essentially copy new elements to desired positions in a destination register. In this context, these desired positions are the lanes that contain inactive elements. The active lanes are identified by a small bitmask (or simply mask), where the \(i{\text {th}}\) bit corresponds to the \(i{\text {th}}\) SIMD lane. An SIMD lane is active if the corresponding bit is set, and vice versa. Thus, the bitwise complement of the given mask refers to the inactive lanes and, therefore, to the write positions of new elements. We distinguish between two cases as follows: (i) where new elements are copied from a source memory address and (ii) where elements are already in vector registers.
In the following, we frequently use various constant values, which we write in capital letters. For instance,
 and
and
 refer to constant values where all bits are zero or one, respectively. The vector constant
refer to constant values where all bits are zero or one, respectively. The vector constant
 contains an integer sequence starting at 0 and
contains an integer sequence starting at 0 and
 refers to the number of SIMD lanes.
refers to the number of SIMD lanes.
4.1 Memory to register
Refilling from memory typically occurs in the table scan operator, where contiguous elements are loaded from memory (assuming a columnar storage layout). AVX-512 offers the convenient

 instruction that loads contiguous values from memory directly into the desired SIMD lanes (cf., Fig. 2). One mask instruction (
instruction that loads contiguous values from memory directly into the desired SIMD lanes (cf., Fig. 2). One mask instruction (
 ) is required to determine the write mask and one vector instruction (
) is required to determine the write mask and one vector instruction (
 ) to execute the actual load. Overall, the simple case of refilling from memory is supported by AVX-512 directly out of the box.
) to execute the actual load. Overall, the simple case of refilling from memory is supported by AVX-512 directly out of the box.
The table scan operator typically produces an additional output vector containing the tuple identifiers (TIDs) of the newly loaded attribute values. The TIDs are derived from the current read position and are used, for example, to (lazily) load attribute values of a different column later on or to reconstruct the tuple order. Figure 3 illustrates, how the content of the TID vector register is updated, using the read position and write mask from Fig. 2.
4.2 Register to register
Moving data between vector registers is more involved. In the most general case, we have a source and a destination register that contain both active and inactive elements at random positions. The goal is to move as many elements as possible from the source to the destination. This can be achieved using a single masked
 instruction. But before the permutation instruction can be issued, the permutation indices need to be computed, based on the positions of active elements in the source and the destination vector registers. This is illustrated in Fig. 4, where, as in the previous examples, the write mask refers to the inactive lanes in the destination register. In total, three vector instructions are required to compute the permutation indices and an additional permutation mask. The latter is required in case the number of active elements in the source is smaller than the number of empty lanes in the destination vector. In that case, the destination register still contains some inactive lanes, and the corresponding bitmask must be updated accordingly.
instruction. But before the permutation instruction can be issued, the permutation indices need to be computed, based on the positions of active elements in the source and the destination vector registers. This is illustrated in Fig. 4, where, as in the previous examples, the write mask refers to the inactive lanes in the destination register. In total, three vector instructions are required to compute the permutation indices and an additional permutation mask. The latter is required in case the number of active elements in the source is smaller than the number of empty lanes in the destination vector. In that case, the destination register still contains some inactive lanes, and the corresponding bitmask must be updated accordingly.
Once the permutation indices are computed, elements can be moved between registers accordingly. Notably, the algorithm can be adapted to move elements directly instead of computing the permutation indices first. However, if elements need to be moved between more than one source/destination vector pair, the additional cost of computing the permutation amortizes immediately with the second pair. In practice, the permutation is typically applied multiple times, for example, when multiple attributes are pushed through the pipeline or to keep track of the TIDs.
In the general case, there are no guarantees about the number of (active) elements nor their positions within the vector register. For example, the elements in the source may not be entirely consumed or the destination vector may still contain inactive elements. Thus, it is necessary to update source and destination masks accordingly. Updating the destination mask is straightforward by using a
 with the previously computed permutation mask. Updating the source mask is less obvious as illustrated in Fig. 5. As the figure shows, updating the source mask is as expensive as preparing the permutation. However, if it is guaranteed that all source elements fit into the destination vector, this phase of the algorithm can be skipped altogether. Listing 1 shows the full algorithm formulated in C++.
with the previously computed permutation mask. Updating the source mask is less obvious as illustrated in Fig. 5. As the figure shows, updating the source mask is as expensive as preparing the permutation. However, if it is guaranteed that all source elements fit into the destination vector, this phase of the algorithm can be skipped altogether. Listing 1 shows the full algorithm formulated in C++.
In summary, a typical refill looks as follows:

4.3 Variants
Depending on the position of the elements, cheaper algorithms can be used. Especially when the vectors are in a compressed state, meaning that the active elements are stored contiguously, it is considerably cheaper to prepare the permutation (compare Listing 1 and 2). Compared to the first algorithm, which can permute elements from/to random positions, the second algorithm does not need any bit masks to refer to the active lanes. Instead, it is sufficient to pass in the number of active elements. In Listing 2, we refer to these numbers as
 and
and
 . Based on these, the permutation indices, as well as the permutation mask, can be computed without any crosslane operations, such as compress/expand. A noteworthy property of the second SIMD algorithm is that the source vector remains in a compressed state even if not all elements fit into the destination vector.
. Based on these, the permutation indices, as well as the permutation mask, can be computed without any crosslane operations, such as compress/expand. A noteworthy property of the second SIMD algorithm is that the source vector remains in a compressed state even if not all elements fit into the destination vector.

These two foundational SIMD algorithms cover the extreme cases where (i) active elements are stored at random positions and (ii) active elements are stored contiguously. Based on these cases, the algorithms can easily be adapted so that only one vector needs to be compressed, which is useful when vector registers are used as tiny buffers because those should always be in a compressed state to achieve the best performance. In total, there are four different algorithms. Each algorithm has two different flavors: (i) where all elements from the source register are guaranteed to fit into the destination register or (ii) where not all elements can be moved and therefore elements remain in the source register. We do not show all variants here, but have released the C++ source codeFootnote 1 under the BSD license.

SIMD lane utilization using different strategies. In a, no refilling is performed to visualize the divergence. b Uses the consume everything strategy, which performs refills when the utilization falls below 75%. The dashed purple lines indicate a write to buffer registers, black lines a read. c shows a partial consume throughout the entire pipeline with the minimum required utilization set to 50%. Lanes colored in purple are protected (color figure online)
5 Refill strategies
We discuss the integration of these refill algorithms in data-centric compiled query pipelines. Such pipelines turn a query operator pipeline into a for-loop, and the code generated by the various operators is nested bottom-up in the body of such a loop [18]. Relational operators in this model generate code in two methods, namely,
 and
and
 , which are called in a depth-first traversal of the query tree:
, which are called in a depth-first traversal of the query tree:
 code is generated before generating the code for the children, and
code is generated before generating the code for the children, and
 afterward.
afterward.
The main idea of data-centric execution with SIMD is to insert checks for each operator that control the number of tuples in play, i.e., if-statements nesting the rest of the body. Such an if-statement ensures that its body only gets executed if the SIMD registers are sufficiently full. Generally speaking, operator code processes input SIMD data computed by the outer operator and refills the registers it works with and the ones it outputs.
We identify two base strategies for applying this refilling.
5.1 Consume everything
The consume everything strategy allocates additional vector registers that are used to buffer tuples. In the case of underutilization, the operator defers the processing of these tuples. This means the body will not be executed in this iteration (if-condition not satisfied) but instead (else) the active tuples will be moved to these buffer registers. It uses the refill algorithms from the previous section both to move data to the buffer and to emit buffered tuples into the unused lanes in a subsequent iteration. Listing 3 shows the code skeleton as it would be generated by such a buffering operator. The
 parameter specifies when a refill is triggered during query execution. Depending on the situation, the costs for refilling might not amortize if only a few lanes contain inactive elements. But if the remaining pipeline is very expensive, setting the threshold to the number of SIMD lanes could be the best option. The important thing to note here is that all SIMD lanes are empty when the control flow returns to the previous operator, thus we call it consume everything.
parameter specifies when a refill is triggered during query execution. Depending on the situation, the costs for refilling might not amortize if only a few lanes contain inactive elements. But if the remaining pipeline is very expensive, setting the threshold to the number of SIMD lanes could be the best option. The important thing to note here is that all SIMD lanes are empty when the control flow returns to the previous operator, thus we call it consume everything.
Compared to a scalar pipeline, this strategy only requires a minor change to the push model: handling a special case when the pipeline execution is about to terminate, flushing the buffer(s). The essence is that buffering only takes place in SIMD registers and it specifically does not cause extra in-memory materialization.
Figure 6a, b illustrates the effects of applying a refill strategy to a query pipeline by visualizing the SIMD lane utilization over time. The structure of the query is similar to the one shown in Fig. 1 and consists of a scan, a selection, a join, and a sink to where the output is written. The stage indicator on top of the plot refers to the node in the control flow graph in Fig. 1. In Fig. 6a, the query is executed without divergence handling, and the white areas refer to underutilization. Figure 6b visualizes the same workload with in-register buffering, following consume everything semantics. The purple and black vertical lines indicate that tuples are written to the buffers, or read from the buffer, respectively. Compared to the divergent implementation, the lane utilization has significantly increased, and the overall execution time has reduced. In this example, we require the utilization to be at least 75% (six out of eight lanes need to be active). Underutilization is observed only when the execution is about to finish, which triggers a pipeline flush, where all (potentially) buffered tuples need to be processed regardless of the minimum utilization threshold.

5.2 Partial consume
As the name suggests, the second base strategy no longer expects the
 code to process the entire input. The consume code can decide to defer execution by returning the control flow to the previous operator and leave the active elements in the vector registers. New tuples are assigned only to inactive lanes by one of the preceding operators, typically a table scan. Naturally, the active lanes, that contain deferred tuples, must not be overwritten or modified by other operators. We refer to these elements (or to their corresponding lanes) as being protected. Another way of looking at a protected lane is that the lane is owned by a different operator. When an owning operator completes the processing of a tuple, it transfers the ownership to the subsequent operator. Alternatively, if the tuple is disqualified, it gives up ownership to allow a tuple producing operator to assign a new tuple to the corresponding lane.
code to process the entire input. The consume code can decide to defer execution by returning the control flow to the previous operator and leave the active elements in the vector registers. New tuples are assigned only to inactive lanes by one of the preceding operators, typically a table scan. Naturally, the active lanes, that contain deferred tuples, must not be overwritten or modified by other operators. We refer to these elements (or to their corresponding lanes) as being protected. Another way of looking at a protected lane is that the lane is owned by a different operator. When an owning operator completes the processing of a tuple, it transfers the ownership to the subsequent operator. Alternatively, if the tuple is disqualified, it gives up ownership to allow a tuple producing operator to assign a new tuple to the corresponding lane.

Lane protection requires additional bookkeeping on a per operator basis. Each operator must be able to distinguish between tuples that (i) have just arrived, (ii) have been protected by the operator itself in an earlier iteration and (iii) tuples that have already advanced to later stages in the pipeline. To do so, an operator maintains two masks, one that identifies the lanes that are owned by the current operator and another one that identifies lanes that are owned by a later operator. Listing 4 shows the structure of such an operator, where
 and
and
 are part of the operator’s state and
are part of the operator’s state and
 is used to communicate which lanes contain active elements (regardless of their stage).
is used to communicate which lanes contain active elements (regardless of their stage).
Figure 6c shows how the partial consume strategy affects the lane utilization with the minimum lane utilization threshold set to 50%. The lanes colored in purple are in a protected state. Compared to the divergent implementation, the lane utilization has increased. However, if we take protected lanes into account and consider them as idle, the overall utilization decreases. Thus, the example workload, used in Fig. 6, reveals an important drawback. If the lanes become protected in later stages of the pipeline, these lanes can cause significant underutilization in the preceding operators. We discuss this issue, among other things, in the following section.
5.3 Discussion and implications
The two strategies are not mutually exclusive. Within a single pipeline, both strategies can be applied to individual operators as long as buffering operators are aware of protected lanes (mixed strategy). Moreover, the query compiler might decide to not apply any refill strategy to certain operators. Especially, when a sequence of operators is quite cheap, divergence might be acceptable as long as the costs for refill operations are not amortized. Naturally, this is a physical query optimization problem that we will leave for future work. Nevertheless, we briefly discuss the advantages and disadvantages, as this is the first work in which we present the basic principles of vector-processing in compiled query pipelines.
As mentioned above, consume everything requires additional registers, which increases the register pressure and may lead to spilling. partial consume allocates additional registers as well, but these are restricted to (smaller) mask registers. Therefore, it is unlikely to be affected by (potential) performance degradation due to spilling.
The second major difference lies in the cost of refilling empty lanes. In a pipeline that follows the partial consume strategy, the very first operator, that is, the pipeline source, is responsible for refilling empty lanes. If other operators experience underutilization, they return the control flow to the previous operator while retaining ownership of the active lanes. This cascades downward until the source operator is reached, as shown in Fig. 6c. All operators between the pipeline source and the operator that returned the control flow may be subject to underutilization because all lanes in later stages are protected. The costs of refilling, therefore, depend on the length of the pipeline and the costs of the preceding operators. In general, the costs increase in the later stages. Nevertheless, partial consume can improve query performance if it is applied only to the very first operators. By contrast, the refilling costs of buffering operators do not depend on the pipeline length. Instead, the crucial factor governing these costs is the number of required buffer registers. The greater the number of buffers, the greater the number of
 instructions that need to be executed, whereas the number of required buffers depends on (i) the number of attributes passed along the pipeline and optionally on (ii) the number of registers required to save the internal state of the operator (e.g., a pointer to the current tree node).
instructions that need to be executed, whereas the number of required buffers depends on (i) the number of attributes passed along the pipeline and optionally on (ii) the number of registers required to save the internal state of the operator (e.g., a pointer to the current tree node).
6 Evaluation
We evaluate our approach with two major sources of control flow divergence, (i) predicate evaluation as part of a table scan and (ii) a hash join. Additionally, we experiment with a more complex operator, an approximate geospatial join. The experiments were conducted on an Intel Skylake-X (SKX) and an Intel Knights Landing (KNL) processor (cf., Table 1). The experiments were implemented in C
 and compiled with GCC 5.4.0 at optimization level three (
and compiled with GCC 5.4.0 at optimization level three (
 ) and the target architecture set to
) and the target architecture set to
 . If not stated otherwise, we ran the experiments in parallel using two threads per core.Footnote 2 We dispatched the work in batches to the individual threads using batch sizes between \(2^{16}\) and \(2^{20}\) tuples. On the KNL platform, we placed the data in high-bandwidth memory (HBM); otherwise, the experiments would have been dominated by memory stalls. To measure the throughputs, we let each experiment run for at least three seconds, possibly consuming the input data multiple times.
. If not stated otherwise, we ran the experiments in parallel using two threads per core.Footnote 2 We dispatched the work in batches to the individual threads using batch sizes between \(2^{16}\) and \(2^{20}\) tuples. On the KNL platform, we placed the data in high-bandwidth memory (HBM); otherwise, the experiments would have been dominated by memory stalls. To measure the throughputs, we let each experiment run for at least three seconds, possibly consuming the input data multiple times.
6.1 Table scan
To evaluate the effects of divergence handling in table scans, we integrate our refill algorithms into the AVX-512 implementation of TPC-H Query 1 of Gubner et al. [6]. Additionally, we implemented and integrated the materialization approach as proposed by Menon et al. in [16].
From a high-level perspective, TPC-H Query 1 (or short Q1) is a structurally simple query that operates on a single fact table (lineitem) with a single scan predicate. It involves several fixed-point arithmetic operations in the aggregation based on the group by clause. In total, five additional attributes are accessed to compute eight aggregated values per group. Almost all tuples survive the selection (i.e., selectivity \(\approx \) 0.98). Therefore, in its original form, Q1 does not suffer from control flow divergence. To simulate control flow divergence and the resulting underutilization of SIMD lanes, we vary the selectivity of the scan predicate on the shipdate attribute.
We evaluate and compare a scalarFootnote 3 non-SIMD) implementation with four AVX-512 implementations:
Divergent: The divergent implementation refers to the implementation published by the authors of [6], with a minor modification. In the original version, all tuples are pushed through the query pipeline and disqualified elements are ignored in the final aggregation by setting the lane bitmask accordingly. For our experiments, we introduced a branch behind the predicate evaluation code, which allows to return the control flow to the scan operator iff all SIMD lanes contain disqualified elements. In the case of Q1, the predicate is evaluated on 16 elements in parallel.
Partial/Buffered: The partial and buffered implementations make use of our refill algorithms. A major difference to the divergent implementation is that it can no longer make use of aligned SIMD loads. Instead, it relies on the gather instruction to load subsequent attribute values. The select operator, therefore, produces a tuple identifier (TID) list that identifies the qualifying tuples. The subsequent operators use the TIDs to compute the offset from where to load the additional attributes. Both implementations are parameterized with the minimum lane utilization threshold, which limits the degree of underutilization.
Materialization: The materialization implementation makes use of small (memory) buffers to consecutively store the output. Similarly to our approach, the select operator produces a TID list. The code of the subsequent operator(s) is executed when the buffer is (almost) full. The buffered TID list is then consumed (scanned) similarly to a table scan in the subsequent operator. Notably, the output contains only TIDs that belong to qualifying tuples, which is in contrast to our approach, where SIMD lanes may contain non-qualifying tuples, depending on the chosen threshold.
Figure 7a shows the performance results for varying selectivities (between 0.00001 and 1.0) on SKX. In the extreme cases, all implementations perform similarly. Interestingly, this includes the scalar implementation, which indicates that the SKX processor performs extremely well with respect to IPC, branch prediction, and out of order execution. With intermediate selectivities, divergence handling can make a significant difference. For instance, with \(\hbox {sel} = 0.01\) the difference between the divergent and materialization implementation is 2.6 billion tuples per second (1.5 billion over scalar). The graph also shows that the materialization dominates over almost the entire range. Our approach (buffered) can compete, but is slightly slower in most cases. On KNL (Fig. 7b), we observed similar effects. The most important difference is that the divergent SIMD implementation is significantly slower than the scalar implementation with selectivities larger than 0.0001. Divergence handling extends the range in which SIMD optimizations become beneficial.
For this experiment, we varied the utilization threshold for partial and buffered as well as the buffer size for materialization and we reported only the best performing variant. In the following, we investigate the impact of these parameters. Figure 8a shows the performance of the materialization approach for varying buffer sizes and a fixed selectivity (\(\hbox {sel} = 0.01\)). Peak performance for Q1 is achieved with a memory buffer of size 1024 elements or larger.
In Fig. 8b, we vary the SIMD lane utilization threshold for our approaches. The performance of the buffered implementation increases with the threshold. Peak performance is reached when only qualifying tuples pass the select operator \((\hbox {threshold} = 16)\). But the performance only gradually increases for a threshold \(\ge 6\). The reason for this behavior is that non-qualifying tuples only cause computational overhead in the remaining pipeline but no memory accesses, which would be significantly more expensive. On the other hand, the partial consume strategy favors a threshold that is approximately half the number of SIMD lanes. If the threshold is too low (left-hand side), many non-qualifying tuples pass the filter, and if it is set too high (right-hand side), the control flow is often returned to the scan code to fetch (a few) more values.
6.2 Hashjoin
Probing a hash table is a search operation in a pointer-based data structure and therefore a prime source of control flow divergence. Here, we evaluate the very common foreign-key join of two relations followed by (scalar) aggregations. The primary key relation constitutes the build size in such a way that the join is non-expanding, i.e., for a probe tuple, at most one join partner exists. The two input relations each have two 8-byte integer attributes: a key and a value. The relations are joined using the keys. Afterward, three aggregations are computed on the join result: the number of tuples, the sum of the values from the left input relation, and the sum of the values from the right input relation. Our hash table implementation stores the first key-value pair per hash bucket in the hash table dictionary. In case of collisions, additional key-value pairs are stored in a linked list per hash bucket.
We evaluate and compare a scalar (non-SIMD) implementation with four AVX-512 implementations:
Divergent: This SIMD implementation handles eight tuples in parallel. The lane bitmask is used to keep track of disqualified tuples, such that they can be ignored at the end of the pipeline. As in the table scan evaluation, we add a branch to allow for an early return to the beginning of the pipeline iff all SIMD lanes contain disqualified tuples. We introduce this branch after the first hash table lookup, i.e., it is triggered when all probe tuples fall into empty hash buckets.
Partial/Buffered: These implementations make use of our in-register refill algorithms. In contrast to the table scan discussed in 6.1, the hash table example uses only few relation attributes. Therefore, instead of loading the additional attributes using gather, here all attributes (i.e., key and value) are passed through the pipeline. If the number of active SIMD lanes drops below the minimum lane utilization threshold, a refill is performed.
Materialization: Menon et al. [16] propose operator fusion, which introduces buffers between operators to compact the stream of tuples flowing through a pipeline. Here, we introduce an intra-operator buffer to further densify the stream of tuples. At the beginning of the pipeline, we load key-value pairs from the probe side input, and compute the hash value and the pointer to the hash table dictionary. We store these key-value pairs and pointers in an input buffer. From this buffer, we then lookup eight pointers in the hash table in parallel, and determine if (i) we found a match, (ii) we need to follow a chain (further), or (iii) there is no match. Unfinished tuples (case (ii)) are written back into the input buffer with an updated pointer; matching tuples (case (i)) are directly pushed to the subsequent aggregation operator without further buffering, which is not in line with [16], where materialization happens on operator boundaries. We also implemented a “fully” materialized version where the matches are first stored in an output buffer before the aggregation code is executed. However, our experiments have shown that two memory materializations are more expensive.
Figures 9 and 10 show the performance results for varying hash table sizes (between 10 KiB and 45 MiB). The hash table size is chosen depending on the build input size. We size the hash table dictionary so that it has the same number of buckets as there are build tuples. Among all evaluated approaches, as well as both platforms, the throughput shrinks with growing hash table sizes. The overall throughput on Knights Landing is about twice as high as on Skylake-X, even though the performance of Skylake-X can be increased by 50% by using Hyper-Threading. On Skylake-X (Fig. 9a, b), as expected, a sharp performance decrease happens when the hash table grows beyond the size of the L2 cache at around 1 MiB, and at around 10 MiB when it exceeds the L3 cache. For large hash tables, that do not fit into the cache, all approaches converge. This has also been observed in earlier work, for instance, by Polychroniou et al. [21] and by Kersten et al. [9]. In these cases, partitioning the hash table might help (cf. the radix partitioning join proposed by Kim et al. [10]), but this is out of scope for this paper.
When the hash table is small enough to fit into the L1 or L2 cache, all SIMD approaches outperform the scalar baseline: Irrespective of the SIMD divergence handling deployed by the individual approaches, they all reach a higher throughput than the scalar approach. For larger hash tables, SIMD divergence no longer dominates the performance, and thus the scalar approach reaches similar throughput levels (using 10 threads) or even higher throughput (using 20 threads) than some SIMD variants. For the whole evaluated range of hash table sizes, the partial and buffered approaches that make use of the introduced refill strategies outperform or are on par with the divergent SIMD approach. Using 20 threads, the buffered approach achieves up to 32% higher throughput than the divergent approach, while the partial approach outperforms the divergent one by up to 19%.
When the hash table fits into the L1 cache, the buffered approach defeats the materialization approach by up to 8%. When the hash tables grow, the materialization approach dominates all other approaches. Two contradicting influences determine whether the materialization approach outperforms our divergence-handling approaches: First, the materialization approach can hide memory latencies better than the buffered and partial approaches because more memory is accessed at the same time (i.e., multiple outstanding loads). This is shown in Fig. 9a and more severely in Fig. 9b when the hash table is large, because it then resides in slower memory. Second, the materialization approach suffers from the higher number of issued instructions, i.e., load and store instructions. In particular, when the hash table fits into L1, the number of instructions can become the limiting factor. On the Knights Landing platform in particular, the materialization approach has a significantly lower throughput compared to the other SIMD variants (Fig. 10). In contrast to the table scan, which we evaluated in Sect. 6.1, the materialization buffer is read and written in the same loop multiple times—during index lookup, which exceeds the limited out-of-order execution capabilities of KNL.
In Fig. 11a, b, we vary the SIMD lane utilization threshold for the partial and buffered approaches. Hyper-Threading, i.e., using 20 threads instead of 10, increases throughput by about 50%. In general, a higher threshold, i.e., less inactive SIMD lanes and more refills, results in a higher throughput. There is little change in throughput when setting the threshold to six, seven or all eight tuples. This is because in most hash table lookups, only a few of the eight tuples need to be kept for additional pointer lookups in the collision chains. As a result, almost no refills are done differently when choosing six, seven or eight as the threshold. The buffered approach is more sensitive to the chosen threshold. For a low threshold, the partial approach reaches a higher throughput, but that changes at threshold 3 (using 10 threads) or 5 (using 20 threads). As mentioned, only few tuples need to be kept for additional lookups. Thus, only few tuples need to be buffered in the buffered approach, while the partial approach suffers from underutilization when frequently performing refills in the table scan.
Figure 11c focuses on the materialization approach, varying the buffer size between eight and 8192 tuples and a fixed build cardinality (hash table size \(\approx \) 128 KiB). For the chosen configuration, the scalar approach reaches a throughput of 1747 Mtps. For small buffers, e.g., 8 tuples, the scalar approach outperforms the materialization approach. The materialization approach with an 8-tuple buffer is conceptually similar to the buffered approach with a SIMD line utilization threshold of 1. Both use a buffer the size of one SIMD vector. In the buffered approach, this buffer lives in registers, while the materialization approach stores it in memory. As a result, the buffered approach outperforms the materialization approach with a throughput of 1964 Mtps (i.e., about 2 billion tuples per second). A buffer size between 128 and 1024 results in the best performance of the materialization approach. The throughput shrinks gracefully when the buffer size is further increased. This is an effect of the chosen workload, especially the number of attributes beside the join attribute.
Two additional parameters affect throughput in the hashjoin evaluation: First, the match probability describes how likely a tuple from the probe side finds a join partner in the hash table. We vary this probability between 0.01 and 1. A low match probability, therefore, results in more disqualified tuples, which—depending on the approach—in turn leads to more ignored SIMD lanes, more refills, or a worse VPU utilization. Figure 12a shows that the buffered approach, using the proposed refill strategies, outperforms both preexisting approaches, scalar and divergent, irrespective of the match probability. The scalar approach is competitive with the SIMD approaches for low match probabilities. With few matches, the scalar approach can often exit the pipeline early, which leads to the high throughput rates we observed. The divergent approach, on the other hand, suffers from extreme underutilization because frequently only few SIMD lanes stay active due to the low match probability. With a match probability of 50%, branches are mispredicted in the scalar approach, and its throughput subsequently tanks. When the match probability approaches 100%, almost all probe tuples find a non-empty hash bucket that then needs to be inspected further. Furthermore, the final aggregation becomes more expensive as more tuples make it into the join result. The scalar approach, therefore, performs best for low match probabilities and worst for a match probability of around 50%, and cannot fully recover its throughput even for a match probability of 100%. When looking at the SIMD approaches, we observe that the throughput difference between the divergent approach and our novel refill approaches increases with the match probability. A higher match probability comes along with more active SIMD lanes after the first lookup in the hash dictionary. Then, more divergence happens because these tuples will have to traverse collision chains of different lengths. The divergence-handling buffered and partial approaches can, therefore, outperform the divergent approach for high match probabilities.
Second, we define the hash table’s load factor as the number of buckets in the hash table divided by the number of keys stored in the hash table. While the load factor has been kept constant in all previous experiments (\(=1.0\)), in real scenarios, the hash table size is not only determined by the size of the build side input, but also by the set load factor. With a low load factor, more collisions in the hash table occur, resulting in longer chains. With longer chains, the variance of the number of pointers that need to be followed to perform the hash table probe increases. This variance directly translates to higher SIMD divergence. A low load factor, therefore, leads to worse VPU utilization in the divergent approach, which can then be mitigated by applying the proposed in-register refill strategies. Figure 12b shows how the load factor affects the throughputs reached by the different approaches. The hash table for load factor 4 is 16 times as big as the hash table for load factor 0.25. Over all approaches, the throughput of the bigger hash table is about three times as high as for the smaller one. For high load factors, the scalar approach performs well. This is because for high load factors, fewer and shorter collision chains exist. When zero of the eight tuples in a vector need to follow a chain, there is not SIMD divergence. Subsequently, for especially high load factors like 4, there is little difference between all approaches.
6.3 Approximate geospatial join
In the following, we evaluate and compare our approach with a modern and more complex operator, an approximate geospatial point-polygon join. Our approximate geospatial join [11] uses a quadtree-based hierarchical grid to approximate polygons. Figure 13 shows such an approximation for the neighborhoods in New York City (NYC). The grid cells are encoded as 64-bit integers and are stored in a specialized radix tree, where the cell size corresponds to the level within the tree structure (larger cells are stored closer to the root node and vice versa). During join processing, we perform (prefix) lookups on the radix tree. Each lookup is separated into two stages: First, we check for a common prefix of the query point and the indexed cells. The common prefix allows for the fast filtering of query points. If the query point does not share the common prefix, there are no join partners. The actual tree traversal takes place in the second stage. We traverse the tree starting from the root node until we hit a leaf node (which contains a reference to the matching polygon).
An important property of our approximate geospatial join operator is that it can be configured to guarantee a certain precision. In the experiments, we used 60-, 15-, and 4-meter precision (as in [11]). The higher the precision guarantee, the smaller are the cells at the polygon boundaries, which in turn increases the total number of cells and, more importantly, the height of the radix tree. In general, the probability of control flow divergence during index lookups increases with the tree height. Throughout our experiments, the tree height is \({\le }\,6\).
In our experiments, we join the boroughs, neighborhoods, and census blocks polygons of NYCFootnote 4 with randomly generated points, uniformly distributed within the minimum bounding box of the corresponding polygonal dataset. The datasets vary in terms of the total number of polygons and complexity (with respect to the number of vertices).
Table 2 summarizes the relevant metrics of the polygon datasets, and Table 3 summarizes the metrics of the corresponding radix tree, including the probability distribution of the number of search steps during the tree traversal.
6.3.1 Query pipeline
The query pipeline of our experiments (point-polygon join) consists of four stages:
- (1)
Scan point data (source)
- (2)
Prefix check
- (3)
Tree traversal
- (4)
Output point-polygon pairs (sink)
Stages (2) and (3) are subject to control flow divergence, with (3) being significantly costlier than (2). For simplicity, the produced output (point-polygon pairs) is not further processed. We compile the pipeline in three different flavors:
Divergent: Refers to the baseline pipeline without divergence handling, thus the pipeline follows consume everything semantics. The code of subsequent operators is executed if at least one lane is active.
Partial: The partial consume strategy is applied to stages (2) and (3), which also affects the scan operator because it needs to be aware of protected lanes.
Buffered: Follows consume everything semantics with register buffers in stage (3). We check the lane utilization after each traversal step. Divergence in stage (2) is not handled at all.
Materialization: The integration of memory materialization is similar to the one used with the hash join operator (cf., Sect. 6.2).
6.3.2 Results
Figure 14 shows the performance results in million tuples per second on KNL using 128 threads. We observe that refilling from register buffers improves the overall throughput by up to 20% \(({=}\,870\,\hbox {mtps})\) when joining with the boroughs or neighborhood polygons. The effect of divergence handling falls below 10% with the census blocks polygons where the index structure is more than 1 GiB in size. In that case, the memory subsystem is the limiting factor.
As expected, the partial consume strategy exacerbates the divergence issue in most cases (cf., Sect. 5.3), resulting in a 53% performance degradation in the worst case.
The materialization approach performs poorly on KNL. The throughput is similar to the scalar implementation, thus canceling out all SIMD optimizations. As in previous benchmarks, we observed a significantly better performance on SKX. Here, the materialization approach is on par with the buffered pipeline: in case of small index structures (boroughs) slightly worse, and with large indexes (census) slightly better. In the latter case, the materialization approach helps to hide memory latencies through out-of-order execution.
Unlike the previous experiments, the optimal lane utilization threshold for the buffered approach is less than the number of SIMD lanes (cf., Fig. 15), which is due to the higher refilling costs involved in the geojoin operator. During the radix tree traversal, refilling affects five vector registers, whereas in the hash join experiment, refilling affects three registers; and only one in the table scan experiment. The optimal threshold for the partial approach is 1, indicating that a refill from the pipeline source is not efficient.
In the experiment above, all points pass the prefix check stage (2) and therefore cause an radix tree traversal. In the following, we also apply divergence handling on the second stage of the pipeline and we changed the workload so that a certain amount of points are disqualified in that stage. We compiled the query pipeline with several combinations of the different approaches. We refer to it using the first letter of the approach (Divergent, Buffered, Partial, and Materialization). For instance, PB refers to the pipeline that uses partial consume in stage two and in-register buffering in the third stage, and BB uses buffering in both stages. Figure 16 shows the results for the neighborhood/4 meter precision workload with varying selectivities. We observe an 8% performance decrease when the buffered approach is applied to stages 2 and 3, and the selectivity remains at 1.0. In contrast, the materialization approach adds a significantly larger overhead (35% decrease). If materialization is applied in both pipeline stages, the performance is worse compared to the pipeline, where it is applied only in the tree traversal stage. Overall, the performance difference for lower selectivities is relatively small with the partial and buffered approaches: \({+}\) 5% with buffering applied in both stages, \({-}\) 7% when partial consume is applied in stage 2 and buffering in stage 3. Compared to the divergent pipeline, lane refilling increases the throughput of the neighborhood workload by up to 30% with lower selectivities.
6.4 Overhead
In our final experiment, we evaluate the overhead of divergence handling with a varying number of attributes. To quantify the overhead, we use a very simplistic query that consists of a simple selection and a scalar aggregation (
 ). Divergence is handled immediately after the selection and before the aggregation. In that scenario, we expect the divergent pipeline to perform best, as the remainder of the pipeline only consists of a single addition and thus the benefits of refilling are close to zero.
). Divergence is handled immediately after the selection and before the aggregation. In that scenario, we expect the divergent pipeline to perform best, as the remainder of the pipeline only consists of a single addition and thus the benefits of refilling are close to zero.
In the following, we consider two different selectivities:
\(\hbox {sel}=1\): For in-register buffering, this situation is the one with the lowest overhead, as the tuples are passed through to the subsequent operator and the buffer registers are not used altogether (cf. Listing 3). Thus, the overhead is rather small, as it effectively consists of a
 to determine the number of active lanes and a branch instruction. The same applies for partial consume pipelines.
to determine the number of active lanes and a branch instruction. The same applies for partial consume pipelines.\(\hbox {sel} = 0.125 = 1/\texttt {LANE\_CNT}\): A selectivity of \(1/\texttt {LANE\_CNT}\) results in one active lane per iteration (on average) and thus represents the most write-intensive case for in-register buffering. That is, the refill algorithm, which moves active elements to the buffer registers, is executed in almost every iteration. The partial consume strategy, on the other hand, suffers from lane underutilization caused by lane protection, and thus, the lower part of the pipeline is executed more frequently.
Throughout all experiments, the pipelines are 8-way data-parallel and we set the minimum lane utilization threshold to 6 for buffered and 4 for partial; the size of memory buffers are fixed to 1024 elements (\({=}\) 8 KiB). The number of attributes is varied within the range [1, 32].
Figure 17 summarizes the results for both evaluation platforms. On KNL, all approaches perform similarly with up to four attributes and the overhead, i.e., the performance difference to the divergent pipeline is barely measurable. The materialization approach degrades significantly when the number of attributes increases (2.5 CPU cycles per tuple per thread compared to 0.14 cycles for divergent). The throughput of the buffered approach degrades as well, which is also attributed to memory materializations. The high register file pressure forces the compiler to evict values to memory. Even though the buffer registers are not used in the case of \(\hbox {sel}=1\), register allocation is static and happens at query compilation time when the actual selectivity is not known. Therefore, a performance degradation can be observed even if register buffers are not used at query runtime. In contrast, the partial consume pipelines are on par with the divergent pipelines.
On the SKX platform, the performance degrades more steeply with an increasing number of attributes. In case of \(\hbox {sel}=1\), the throughput of the materialization approach decreases linearly with the number of attributes. Compared to KNL, the number of attributes has a higher impact on the overall performance on SKX. For instance, in-register buffering is \(4\, \times \) faster on KNL with \(\hbox {sel}=1\) and \(3.6\, \times \) faster with \(\hbox {sel}=0.125\). For \(\hbox {sel}=0.125\) and a single projected attribute, we measure an overhead of approximately 0.1 cycles per tuple for buffered and 0.15 cycles per tuple for partial, which is significantly higher than with the materialization approach (0.02 cycles). However, the per attribute overhead of buffered and partial decreases with more projected attributes, whereas the materialization approach shows an increasing overhead with an increasing number of attributes. The crossover point is reached with 8 projected attributes. Afterward, our approaches are consistently faster.
In general, the partial consume approach shows no performance impact when the number of projected attributes increases, which is an expected result, because the bookkeeping overhead about protected lanes is constant, irrespective from the number of projected attributes. The actual overhead of the partial consume strategy depends on the pipeline costs, more precisely on the pipeline fragment before divergence handling (see Sect. 5.3).
7 Summary and discussion
The partial consume strategy shows performance improvements for relatively simple workloads. With more complex workloads, like the geospatial join, we observe severe performance degradations. The reason for that is twofold. (i) Protected lanes inherently cause the underutilization of VPUs (as described in Sect. 5) and (ii) they result in a suboptimal memory access pattern at the pipeline source where the refill happens. In contrast to the consume everything strategy, wherein every iteration exact
 elements are read from memory, a partial consume scan reads at most
elements are read from memory, a partial consume scan reads at most elements. This circumstance reduces the degree of data-parallelism (fewer elements are loaded per instruction) and also leads to unaligned SIMD loads. Even though the access pattern is still sequential, the alignment issues can reduce the load throughput by up to 25% (on our evaluation platforms), which could severely reduce the overall performance of scan-heavy workloads.
elements. This circumstance reduces the degree of data-parallelism (fewer elements are loaded per instruction) and also leads to unaligned SIMD loads. Even though the access pattern is still sequential, the alignment issues can reduce the load throughput by up to 25% (on our evaluation platforms), which could severely reduce the overall performance of scan-heavy workloads.
We found that the materialization approach is very sensitive to the underlying hardware, in particular, on KNL, the approach performs poorly when the buffer is read and written within a tight loop (intra-operator), an effect that could not be observed on SKX. On the other hand, if materialization is applied at operator boundaries and thus written and read only once, it performs similarly or better than in-register buffering, as it benefits from out-of-order execution, which allows the materialization approach to hide memory latencies. Memory access latencies play an important role when the data that is randomly accessed (like a hash table) does not fit into the L1 / L2 cache. In contrast, when the data fits into cache or the workload is more compute-heavy, the in-register buffering approach dominates because the buffers provide much faster access.
The SIMD lane utilization threshold (refill more often vs. VPU underutilization) has a big impact on the buffered approach and less impact on partial. As buffered shows better performance in general, this parameter is important. Choosing the highest possible threshold shows the best results in simple workloads, so going back down the pipeline to refill the vector is always better than having inactive lanes, we found. So the idea of materialization, where only active (or qualifying) elements are passed along the pipeline, was right in these scenarios. The picture changes with more complex operators like the geojoin, where refilling affects five vector registers. In this case, refilling doesn’t pay off for a single idle SIMD lane. On average, the optimal utilization threshold was 5 out of 8 among the geospatial related experiments.
It remains an open question how the optimal threshold can be predicted at query compilation time, as it depends on hardware, refilling costs, the costs incurred by underutilized lanes, and the actual input data. A possible approach to address this issue is to adaptively adjust the threshold parameter at runtime (per batch or per morsel [14]). Nevertheless, divergence handling cannot fully be disabled once the pipeline has been compiled. One can set the threshold to 1, which is equivalent to a divergent execution, but some overhead remains in the compiled code, namely the population count instruction and the branching logic. For instance, in our geospatial experiments on KNL, we observed an overhead of up to 6% over divergent with the boroughs workload when the utilization threshold is set to one (neighborhoods 3.6%, census 0.6%). Dynamically adjusting the threshold at query runtime provides some flexibility but due to the fact that divergence handling cannot be fully disabled, a database system needs to decide at compilation time whether to enable or disable divergence handling altogether.
Finally, we want to point out that our proposed refill algorithms and strategies are generally applicable to any data processing system that uses AVX-512 SIMD instructions. A prominent open-source representative is Apache Arrow [1] (in combination with Gandiva) which shares many similarities with state-of-the-art relational database systems (e.g., columnar storage, JIT-compilation, and operator fusion). Further, our approaches are also applicable if the underlying database system uses compression in its storage layer. In particular, when compression is only used on secondary storage, it does not affect query execution. However, recent systems [13, 19] tend to use lightweight compression techniques that allow for the processing of data without explicitly decompressing it. This implies that the degree of data-parallelism can be increased, as more attributes can be packed into a single vector register. Currently, our buffered approach is limited to 16-way data-parallelism on the KNL and SKX platforms, but it can be easily extended to 64-way data-parallelism for upcoming processors with the AVX-512/VBMI2 instruction set.
8 Conclusions
In this work, we presented efficient refill algorithms for vector registers by using the latest SIMD instruction set, AVX-512. Further, we identified and presented two basic strategies for applying refilling to compiled query pipelines for preventing the underutilization of VPUs. Our experimental evaluation showed that our strategies can efficiently handle control flow divergence. In particular, query pipelines that involve traversing irregular pointer-based data structures, like hash tables or radix trees, can significantly benefit from divergence handling. Especially when the workload is compute-intense or fits into fast caches, our novel approach shows better performance than existing approaches that rely on memory buffers.
Nevertheless, our research also showed that SIMD still cannot live up to the high expectations set by the promising features of the latest hardware, i.e., providing n-way data-parallelism. In practice, SIMD speedups are only a fraction of the advertised degree of data-parallelism, for many reasons, including underutilization. Our refill algorithms address this important reason, yet merely achieve a 2 \(\times \) speedup over scalar code.
Notes
Source code: https://github.com/harald-lang/simd_divergence.
Please note that throughout our (multi-threaded) experiments, we did not observe any performance penalties through downclocking. Both processors KNL and SKX run stable at 1.4 GHz and 4.0 GHz, respectively.
Scalar refers to an implementation which does not use any SIMD instructions. We verified, that the compiler did not auto-vectorize the query pipelines.
References
Apache Arrow. https://arrow.apache.org/
Balkesen, C., Alonso, G., Teubner, J., Özsu, M.T.: Multi-core, main-memory joins: sort vs. hash revisited. PVLDB 7(1), 85–96 (2013)
Balkesen, C., Teubner, J., Alonso, G., Özsu, M.T.: Main-memory hash joins on multi-core CPUs: tuning to the underlying hardware. In: 29th IEEE International Conference on Data Engineering, ICDE 2013, Brisbane, Australia, April 8–12, 2013, pp. 362–373 (2013). https://doi.org/10.1109/ICDE.2013.6544839
Boncz, P.A., Zukowski, M., Nes, N.: MonetDB/X100: hyper-pipelining query execution. In: CIDR 2005, 2nd Biennial Conference on Innovative Data Systems Research, Asilomar, CA, USA, January 4–7, 2005, Online Proceedings, pp. 225–237 (2005). http://cidrdb.org/cidr2005/papers/P19.pdf
Chhugani, J., Nguyen, A.D., Lee, V.W., Macy, W., Hagog, M., Chen, Y., Baransi, A., Kumar, S., Dubey, P.: Efficient implementation of sorting on multi-core SIMD CPU architecture. PVLDB 1(2), 1313–1324 (2008)
Gubner, T., Boncz, P.: Exploring query compilation strategies for JIT, vectorization and SIMD. In: 8th International Workshop on Accelerating Analytics and Data Management Systems Using Modern Processor and Storage Architectures, ADMS 2017, Munich, Germany, September 1, 2017 (2017)
Kemper, A., Neumann, T.: Hyper: a hybrid OLTP&OLAP main memory database system based on virtual memory snapshots. In: Proceedings of the 27th International Conference on Data Engineering, ICDE 2011, April 11–16, 2011, Hannover, Germany, pp. 195–206 (2011). https://doi.org/10.1109/ICDE.2011.5767867
Kersten, T., Leis, V., Kemper, A., Neumann, T., Pavlo, A., Boncz, P.A.: Everything you always wanted to know about compiled and vectorized queries but were afraid to ask. PVLDB 11(13), 2209–2222 (2018). https://doi.org/10.14778/3275366.3275370
Kim, C., Sedlar, E., Chhugani, J., Kaldewey, T., Nguyen, A.D., Blas, A.D., Lee, V.W., Satish, N., Dubey, P.: Sort vs. hash revisited: fast join implementation on modern multi-core CPUs. PVLDB 2(2), 1378–1389 (2009)
Kipf, A., Lang, H., Pandey, V., Persa, R.A., Boncz, P., Neumann, T., Kemper, A.: Approximate geospatial joins with precision guarantees. In: 34rd IEEE International Conference on Data Engineering, ICDE 2018, Paris, France, April 16–19, 2018 (2018)
Lang, H., Mühlbauer, T., Funke, F., Boncz, P.A., Neumann, T., Kemper, A.: Data blocks: hybrid OLTP and OLAP on compressed storage using both vectorization and compilation. In: Proceedings of the 2016 International Conference on Management of Data, SIGMOD Conference 2016, San Francisco, CA, USA, June 26–July 01, 2016, pp. 311–326 (2016). https://doi.org/10.1145/2882903.2882925
Lang, H., Mühlbauer, T., Funke, F., Boncz, P.A., Neumann, T., Kemper, A.: Data blocks: hybrid OLTP and OLAP on compressed storage using both vectorization and compilation. In: Özcan, F., Koutrika, G., Madden, S., (eds.) Proceedings of the 2016 International Conference on Management of Data, SIGMOD Conference 2016, San Francisco, CA, USA, June 26–July 01, 2016, pp. 311–326. ACM, San Francisco (2016). https://doi.org/10.1145/2882903.2882925
Leis, V., Boncz, P.A., Kemper, A., Neumann, T.: Morsel-driven parallelism: a NUMA-aware query evaluation framework for the many-core age. In: Dyreson, C.E., Li, F., Özsu, M.T. (eds.) International Conference on Management of Data, SIGMOD 2014, Snowbird, UT, USA, June 22–27, 2014, pp. 743–754. ACM, New York (2014). https://doi.org/10.1145/2588555.2610507
Lemire, D., Rupp, C.: Upscaledb: efficient integer-key compression in a key-value store using SIMD instructions. Inf. Syst. 66, 13–23 (2017). https://doi.org/10.1016/j.is.2017.01.002
Menon, P., Pavlo, A., Mowry, T.C.: Relaxed operator fusion for in-memory databases: making compilation, vectorization, and prefetching work together at last. PVLDB 11(1), 1–13 (2017)
Mühlbauer, T., Rödiger, W., Seilbeck, R., Reiser, A., Kemper, A., Neumann, T.: Instant loading for main memory databases. PVLDB 6(14), 1702–1713 (2013)
Neumann, T.: Efficiently compiling efficient query plans for modern hardware. PVLDB 4(9), 539–550 (2011)
Nowakiewicz, M., Boutin, E., Hanson, E., Walzer, R., Katipally, A.: BIPie: fast selection and aggregation on encoded data using operator specialization. In: Proceedings of the 2018 International Conference on Management of Data, SIGMOD’18, pp. 1447–1459. ACM, New York (2018). https://doi.org/10.1145/3183713.3190658
Polychroniou, O., Raghavan, A., Ross, K.A.: Rethinking SIMD vectorization for in-memory databases. In: Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data, Melbourne, Victoria, Australia, May 31–June 4, 2015, pp. 1493–1508 (2015). https://doi.org/10.1145/2723372.2747645
Polychroniou, O., Raghavan, A., Ross, K.A.: Rethinking SIMD vectorization for in-memory databases. In: Proceedings of SIGMOD, pp. 1493–1508 (2015). https://doi.org/10.1145/2723372.2747645
Polychroniou, O., Ross, K.A.: Vectorized bloom filters for advanced SIMD processors. In: 10th International Workshop on Data Management on New Hardware, DaMoN 2014, Snowbird, UT, USA, June 23, 2014, pp. 6:1–6:6 (2014). https://doi.org/10.1145/2619228.2619234
Polychroniou, O., Ross, K.A.: Efficient lightweight compression alongside fast scans. In: Proceedings of the 11th International Workshop on Data Management on New Hardware, DaMoN 2015, Melbourne, VIC, Australia, May 31–June 04, 2015, pp. 9:1–9:6 (2015). https://doi.org/10.1145/2771937.2771943
Ren, B., Agrawal, G., Larus, J.R., Mytkowicz, T., Poutanen, T., Schulte, W.: SIMD parallelization of applications that traverse irregular data structures. In: Proceedings of the 2013 IEEE/ACM International Symposium on Code Generation and Optimization, CGO 2013, Shenzhen, China, February 23–27, 2013, pp. 20:1–20:10 (2013). https://doi.org/10.1109/CGO.2013.6494989
Sitaridi, E.A., Polychroniou, O., Ross, K.A.: Simd-acceleratedregular expression matching. In: Proceedings of the 12th International Workshop on Data Management on New Hardware, DaMoN2016, San Francisco, CA, USA, June 27, 2016, pp. 8:1–8:7 (2016). https://doi.org/10.1145/2933349.2933357
Teubner, J., Müller, R.: How soccer players would do stream joins. In: Proceedings of the ACM SIGMOD International Conference on Management of Data, SIGMOD 2011, Athens, Greece, June 12–16, 2011, pp. 625–636 (2011). https://doi.org/10.1145/1989323.1989389
Zhao, W.X., Zhang, X., Lemire, D., Shan, D., Nie, J., Yan, H., Wen, J.: A general simd-based approach to accelerating compression algorithms. ACM Trans. Inf. Syst. 33(3), 15:1–15:28 (2015). https://doi.org/10.1145/2735629
Zhou, J., Ross, K.A.: Implementing database operations using SIMD instructions. In: Proceedings of the 2002 ACM SIGMOD International Conference on Management of Data, Madison, Wisconsin, June 3–6, 2002, pp. 145–156 (2002)
Acknowledgements
This work has been partially supported by the German Federal Ministry of Education and Research (BMBF) Grant 01IS12057 (FASTDATA and MIRIN) and the DFG Projects NE1677/1-2 and KE401/22. Furthermore, this work is part of the TUM Living Lab Connected Mobility (TUM LLCM) Project and has been partially funded by the Bavarian Ministry of Economic Affairs, Energy and Technology (StMWi) through the Center Digitisation.Bavaria, an initiative of the Bavarian State Government.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
An excerpt of this invited paper in the special issue “Best of DaMoN” appeared in DaMoN 2018.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lang, H., Passing, L., Kipf, A. et al. Make the most out of your SIMD investments: counter control flow divergence in compiled query pipelines. The VLDB Journal 29, 757–774 (2020). https://doi.org/10.1007/s00778-019-00547-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00778-019-00547-y


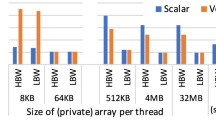


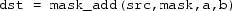 . The addition is performed on the vector components in
. The addition is performed on the vector components in
 and
and
 specified by the
specified by the
 . The remaining elements, where the mask bits are
. The remaining elements, where the mask bits are
 , are copied from
, are copied from
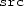 to
to
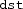 at their corresponding positions.
at their corresponding positions.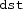 are set to zero if the corresponding bit in the mask is not set. Zero masking is, therefore, (logically) equivalent to merge masking with
are set to zero if the corresponding bit in the mask is not set. Zero masking is, therefore, (logically) equivalent to merge masking with
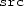 set to zero:
set to zero:
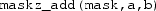
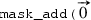
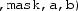 ). Thus, zero masking is a special case of merge masking.
). Thus, zero masking is a special case of merge masking.
















 to determine the number of active lanes and a branch instruction. The same applies for partial consume pipelines.
to determine the number of active lanes and a branch instruction. The same applies for partial consume pipelines.