1 Introduction

Canals play an important role in terms of shortening distance and time in the maritime transportation routes worldwide. Among them, the Suez Canal is a horizontal canal with a total length of 193 km connecting the Red Sea and the Mediterranean Sea, and this can be a key point for maritime transportation. On the other hand, due to its importance, the canal will become a bottleneck if traffic is disrupted, and the serious impact will be wide-ranging. The grounding accident of a container ship in 2021 and the subsequent stagnation of marine transportation are still fresh in our memory.

Many researchers have dealt with the problem of navigation safety of ships running in narrow waterways such as canals. In addition to experimental and analytical studies by Fujino [1] and Eda [2], the authors [3] have also applied similar methods to the navigation safety of a ship sailing near a domestic port. Recently, flow field analysis by CFD [4] has been applied. A characteristic of the problem of navigational safety for ships running in narrow waterways is that special lateral force and yaw moment (these are called asymmetric hydrodynamic forces) act on the ship when navigating near waterway wall. These are caused by the left-right asymmetry of the flow field around the ship navigating near the wall. In the conventional ship maneuvering model in narrow waterways, the asymmetric hydrodynamic forces during straight moving are captured in a tank test as a function of a distance from the center of the waterway, and the analysis was carried out by representing them using derivatives with respect to the distance [1,2,3]. The asymmetric hydrodynamic forces are considered to change not only with the distance from the center of the waterway, but also with the change in the ship’s heading in the waterway. However, there are no available studies on this so far.

In this paper, first, the equation of motion with the added mass expressed explicitly for ship maneuvering near an arbitrary-shaped bank is presented within the potential theory [5]. Then, we apply this to the maneuvering problem for ships in a straight canal. The new theory shows that the hydrodynamic derivative (\(Y_{\psi }, N_{\psi }\)) of the lateral force and the yaw moment with respect to the ship heading cannot be neglected. To confirm this, \(Y_{\psi }\) and \(N_{\psi }\) are measured together with all the hydrodynamic derivatives and added mass in a tank test. Furthermore, using the obtained derivatives, the course stability of a ship sailing in a canal is investigated, and the effect of \(Y_{\psi }\) and \(N_{\psi }\) on the course stability is discussed.

2 Equation of motion and hydrodynamic derivatives on maneuvering for ship in a canal

2.1 Equation of motion of ship in the proximity of arbitrarily shaped bank based on the potential theory

We consider maneuvering motion of a ship navigating in the proximity of an arbitrary-shaped bank. The maneuvering motion of the ship is assumed to be represented by the equations of motion for surge, sway, and yaw in the horizontal plane. In addition, we assume the following.

  1. 1.

    The flow field around the ship is non-viscous, non-compressive and non-rotating, and is expressed by the potential theory.

  2. 2.

    The ship speed is slow, and the free surface is replaced by a rigid wall.

  3. 3.

    Water depth is uniform and constant.

  4. 4.

    The damping force based on viscosity is separately considered and is not affected by the bank.

These assumptions eliminate the need to consider the memory effect due to the free surface and vortices, and the problem can be treated in a quasi-steady manner.

We consider a coordinate system \(o-xyz\) fixed to the ship hull. The longitudinal direction of the ship is the x axis, the transverse direction is the y axis, and the vertical downward direction is the z axis. If the water depth is denoted by h, the bottom is at the position \(z=h\). It is assumed that the ship maneuvers with the longitudinal velocity u, lateral velocity v, and yaw rate r. The disturbance potential \(\phi (t,x,y,z)\), which defines the flow field around the hull, satisfies the Laplace’s equation. The boundary conditions of \(\phi\) are expressed as follows.

$$\begin{aligned} \frac{\partial \phi }{\partial n}= & {} un_1+vn_2+rn_3 \ \ \ \text{ on } S_H \end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial \phi }{\partial n}= & {} 0 \ \ \ \text{ on } S_B \end{aligned}$$
(2)
$$\begin{aligned} \frac{\partial \phi }{\partial z}= & {} 0 \ \ \ \text{ on } z=0 \end{aligned}$$
(3)
$$\begin{aligned} \frac{\partial \phi }{\partial z}= & {} 0 \ \ \ \text{ on } z=h \end{aligned}$$
(4)

Equation (1) is the hull surface boundary condition, Eq.(2) is the bank wall surface boundary condition, Eq. (3) is the free surface condition assuming a rigid wall, and Eq. (4) is the bottom boundary condition. In the equations, \(S_H\) and \(S_B\) represent the hull surface and the bank wall surface, respectively. In Eq. (1), \(n_1\) and \(n_2\) are the x and y axes direction components of the outward direction cosine of the hull surface, respectively. \(n_3\) is the direction cosine component for yaw defined as \(n_3=xn_2-yn_1\), where x and y are the coordinates of the hull surface.

The surge force (\(\hat{F}_1\)), lateral force (\(\hat{F}_2\)), and yaw moment (\(\hat{F}_3\)) acting on the ship are expressed by integrating the pressure on the hull surface, which is expressed by Bernoulli’s equation, as follows.

$$\begin{aligned} \hat{F}_1(t)= & {} -\rho \int \hspace{-2mm}\int _{S_H} \left[ \frac{\partial \phi }{\partial t}+\frac{1}{2}(\nabla \phi )^2 \right] n_1 \textrm{d}S \end{aligned}$$
(5)
$$\begin{aligned} \hat{F}_2(t)= & {} -\rho \int \hspace{-2mm}\int _{S_H} \left[ \frac{\partial \phi }{\partial t}+\frac{1}{2}(\nabla \phi )^2 \right] n_2 \textrm{d}S \end{aligned}$$
(6)
$$\begin{aligned} \hat{F}_3(t)= & {} -\rho \int \hspace{-2mm}\int _{S_H} \left[ \frac{\partial \phi }{\partial t}+\frac{1}{2}(\nabla \phi )^2 \right] (xn_2-yn_1) \textrm{d}S \end{aligned}$$
(7)

where \(\rho\) is the water density. In the equations, we rewrite the terms of \(\partial \phi /\partial t\) as follows [6].

$$\begin{aligned} \hat{F}_1(t)= & {} -\rho \frac{\textrm{d}}{\textrm{d}t}\int \hspace{-2mm}\int _{S_H} \phi n_1\textrm{d}S + \rho \int \hspace{-2mm}\int _{S_H} \left[ \frac{\partial \phi }{\partial n}\frac{\partial \phi }{\partial x} - \frac{1}{2}(\nabla \phi )^2 n_1\right] \textrm{d}S \end{aligned}$$
(8)
$$\begin{aligned} \hat{F}_2(t)= & {} -\rho \frac{\textrm{d}}{\textrm{d}t}\int \hspace{-2mm}\int _{S_H} \phi n_2\textrm{d}S + \rho \int \hspace{-2mm}\int _{S_H} \left[ \frac{\partial \phi }{\partial n}\frac{\partial \phi }{\partial y}- \frac{1}{2}(\nabla \phi )^2 n_2\right] \textrm{d}S \end{aligned}$$
(9)
$$\begin{aligned} \hat{F}_3(t)= & {} -\rho \frac{\textrm{d}}{\textrm{d}t}\int \hspace{-2mm}\int _{S_H} \phi (xn_2-yn_1)\textrm{d}S \nonumber \\{} & {} + \rho \int \hspace{-2mm}\int _{S_H} \left[ \frac{\partial \phi }{\partial n}\left( x\frac{\partial \phi }{\partial y}-y\frac{\partial \phi }{\partial x}\right) - \frac{1}{2}(\nabla \phi )^2 (xn_2-yn_1)\right] \textrm{d}S \end{aligned}$$
(10)

These are basic equations of the hydrodynamic forces acting on the ship in the proximity of the bank.

Equations (8) \(\sim\) (10) have a term of d/dt, which is the hydrodynamic force component proportional to the motion acceleration of the ship. We explicitly consider expressing the hydrodynamic force component proportional to this acceleration to make numerical calculations of the hydrodynamic forces stable. Referring to Eq.(1), we express \(\phi (t,x,y,z)\) in the following form.

$$\begin{aligned} \phi (t,x,y,z) = \sum _{i=1}^{3} U_i(t)\phi _i(t,x,y,z) \end{aligned}$$
(11)

where \(U_1=u\), \(U_2=v\), and \(U_3=r\). The hull surface condition and bank wall surface condition for \(\phi _i(i=1,2,3)\) can be expressed as follows.

$$\begin{aligned} \frac{\partial \phi _i}{\partial n}= & {} n_i \ \ \ \text{ on } S_H \end{aligned}$$
(12)
$$\begin{aligned} \frac{\partial \phi _i}{\partial n}= & {} 0 \ \ \ \text{ on } S_B \end{aligned}$$
(13)

\(\phi _i\) is expressed as follows via the source strength \(\sigma _i\).

$$\begin{aligned} \phi _i(t,P) = \int \hspace{-2mm}\int _{S_H+S_B} \sigma _i(t,Q)G(P;Q) dS \end{aligned}$$
(14)

where \(P=(x,y,z)\) is the field point and \(Q=(\xi ,\eta ,\zeta )\) is the singular point. G(P; Q) is the Green’s function that satisfies Eqs. (3) and (4) by considering an infinite number of mirrored sources with respect to \(z=\pm 2h\)[7].

$$\begin{aligned} G\left( x,y,z;\xi ,\eta ,\zeta \right)= & {} \frac{1}{h}\left[ G_0\left( \tilde{x}-\tilde{\xi },\tilde{y},\tilde{z}-\tilde{\zeta }\right) +G_0\left( \tilde{x}-\tilde{\xi },\tilde{y},\tilde{z}+\tilde{\zeta }\right) \right] \end{aligned}$$
(15)

Here, \(\tilde{}\) is the non-dimensionalized value using the water depth h, and \(G_0\) is expressed as follows.

$$\begin{aligned} G_0(x,y,z)= & {} \left[ x^2+y^2+z^2\right] ^{-1/2} \nonumber \\{} & {} + \sum _{j=1}^{\infty }\left\{ \left[ x^2+y^2+(z+2j)^2\right] ^{-1/2} + \left[ x^2+y^2+(z-2j)^2\right] ^{-1/2}\right\} \end{aligned}$$
(16)

Substituting Eq. (14) into Eqs. (12) and (13) yields the following.

$$\begin{aligned}{} & {} \int \hspace{-2mm}\int _{S_H+S_B} \sigma _i(t,Q) \frac{\partial G(P;Q)}{\partial n} \textrm{d}S = f_H(P) \end{aligned}$$
(17)

where

$$\begin{aligned} f_H(P)= \left\{ \begin{array}{lll} n_i &{} \text{ for } \text{ P } \text{ on } S_H &{} \\ 0 \ \ {} &{} \text{ for } \text{ P } \text{ on } S_B&{} \end{array} \right. \end{aligned}$$
(18)

Equation (17) is an integral equation expressing the boundary conditions of the hull and bank wall with unknown \(\sigma _i\). By solving this equation, \(\sigma _i\) can be obtained.

In Eqs. (8)–(10), the hydrodynamic forces of the first integral term of the right hand side are denoted by \({F}_{Ak}(k=1,2,3)\), and the second integral term is denoted by \({F}_{Dk}(k=1,2,3)\). \({F}_{Ak}\) indicates the terms related to the time derivative of the velocity potential, and \({F}_{Dk}\) represents the terms related to the square of the velocity potential calculated in a quasi-steady manner. Paying attention to the following relationships,

$$\begin{aligned}{} & {} \frac{\textrm{d}n_1}{\textrm{d}t}=-U_3n_2, \ \ \frac{\textrm{d}n_2}{\textrm{d}t}= U_3n_1, \ \ \frac{\textrm{d}n_3}{\textrm{d}t}= U_3\left( n_1-n_2\right) , \end{aligned}$$

\({F}_{Ak}\) is expressed as follows.

$$\begin{aligned} F_{A1}= & {} -\rho \sum _{i=1}^{3}\left[ \dot{U}_i\int \hspace{-2mm}\int _{S_H} \phi _i n_1\textrm{d}S +U_i\frac{\textrm{d}}{\textrm{d}t}\int \hspace{-2mm}\int _{S_H} \phi _i n_1\textrm{d}S -U_iU_3\int \hspace{-2mm}\int _{S_H} \phi _i n_2\textrm{d}S \right] \end{aligned}$$
(19)
$$\begin{aligned} F_{A2}= & {} -\rho \sum _{i=1}^{3}\left[ \dot{U}_i\int \hspace{-2mm}\int _{S_H} \phi _i n_2\textrm{d}S +U_i\frac{\textrm{d}}{\textrm{d}t}\int \hspace{-2mm}\int _{S_H} \phi _i n_2\textrm{d}S +U_iU_3\int \hspace{-2mm}\int _{S_H} \phi _i n_1\textrm{d}S \right] \end{aligned}$$
(20)
$$\begin{aligned} F_{A3}= & {} -\rho \sum _{i=1}^{3}\left[ \dot{U}_i\int \hspace{-2mm}\int _{S_H} \phi _i n_3\textrm{d}S +{U}_i\frac{\textrm{d}}{\textrm{d}t}\int \hspace{-2mm}\int _{S_H} \phi _i n_3\textrm{d}S +{U}_iU_1\int \hspace{-2mm}\int _{S_H} \phi _i n_2\textrm{d}S \right. \nonumber \\{} & {} -\left. {U}_iU_2\int \hspace{-2mm}\int _{S_H} \phi _i n_1dS \right] \end{aligned}$$
(21)

where dot notation (\(\dot{\ \ }\)) means the ordinary derivative with respect to time t. The added mass generated in the j-th direction by the motion mode in the i-th direction is defined as follows.

$$\begin{aligned} m_{ji}= & {} \rho \int \hspace{-2mm}\int _{S_H} \phi _i \frac{\partial \phi _j}{\partial n}dS \end{aligned}$$
(22)

Then, Eqs. (19) \(\sim\) (21) are rewritten as follows.

$$\begin{aligned} F_{A1}= & {} -\sum _{i=1}^{3}\left[ \dot{U}_im_{1i}+U_i\dot{m}_{1i}-U_iU_3m_{2i} \right] \end{aligned}$$
(23)
$$\begin{aligned} F_{A2}= & {} -\sum _{i=1}^{3}\left[ \dot{U}_im_{2i}+U_i\dot{m}_{2i}+U_iU_3m_{1i} \right] \end{aligned}$$
(24)
$$\begin{aligned} F_{A3}= & {} -\sum _{i=1}^{3}\left[ \dot{U}_im_{3i}+U_i\dot{m}_{3i}+{U}_iU_1m_{2i}-{U}_iU_2m_{1i} \right] \end{aligned}$$
(25)

\(F_{Aj}\) can be calculated if the motion of the ship (\(U_i\)), added mass (\(m_{ji}\)), and their time derivatives are known.

\({F}_{Dj}\) is represented as follows.

$$\begin{aligned} {F}_{Dj}= & {} \rho \int \hspace{-2mm}\int _{S_H} \left[ \frac{\partial \phi }{\partial n}\frac{\partial \phi }{\partial x_j} - \frac{1}{2}(\nabla \phi )^2 n_j\right] \textrm{d}S \end{aligned}$$
(26)

where \(\partial /\partial x_1=\partial /\partial x\), \(\partial /\partial x_2=\partial /\partial y\), and \(\partial /\partial x_3= x\partial /\partial y-y\partial /\partial x\) are defined. By substituting Eq.(11) into Eq.(26), \({F}_{Dj}\) is expressed as follows.

$$\begin{aligned} F_{Dj}= & {} \left[ \begin{array}{ccc} D_{23}^{(1)} &{} D_{31}^{(1)} &{} D_{12}^{(1)} \\ D_{23}^{(2)} &{} D_{31}^{(2)} &{} D_{12}^{(2)} \\ D_{23}^{(3)} &{} D_{31}^{(3)} &{} D_{12}^{(3)} \\ \end{array} \right] \left\{ \ \begin{array}{cc} U_2{U}_3 \\ U_3{U}_1 \\ U_1{U}_2 \\ \end{array} \right\} +\dfrac{1}{2} \left[ \begin{array}{ccc} D_{11}^{(1)} &{} D_{22}^{(1)} &{} D_{33}^{(1)} \\ D_{11}^{(2)} &{} D_{22}^{(2)} &{} D_{33}^{(2)} \\ D_{11}^{(3)} &{} D_{22}^{(3)} &{} D_{33}^{(3)} \\ \end{array} \right] \left\{ \ \begin{array}{cc} U_1^2 \\ U_2^2 \\ U_3^2 \\ \end{array} \right\} \end{aligned}$$
(27)

where

$$\begin{aligned} D_{ik}^{(j)}= & {} \rho \int \hspace{-2mm}\int _{S_H} \left[ \frac{\partial \phi _i}{\partial n}\frac{\partial \phi _k}{\partial x_j} +\frac{\partial \phi _k}{\partial n}\frac{\partial \phi _i}{\partial x_j} -\nabla \phi _k\nabla \phi _i n_j\right] \textrm{d}S \end{aligned}$$
(28)

The equation of motion for ship maneuvering in the hull fixed coordinate system is expressed as follows.

$$\begin{aligned} \left. \begin{array}{lll} m(\dot{U_1}-U_2U_3)&=F_{A1} + F_{D1} + F_{V1} + F_{E1} \\ m(\dot{U_2}+U_1U_3)&=F_{A2} + F_{D2} + F_{V2} + F_{E2} \\ I_z\dot{U_3}&=F_{A3} + F_{D3} + F_{V3} + F_{E3} \end{array} \right\} \end{aligned}$$
(29)

where m is the mass of the ship, and \(I_z\) is the moment of inertia around z-axis. \(F_{Vk}\) is damping forces due to fluid viscosity, and \(F_{Ek}\) is external forces, such as propeller thrust and rudder force. By substituting Eqs. (23) \(\sim\) (25) and (27) into Eq. (29), the following equation is obtained.

$$\begin{aligned}{} & {} \left[ \begin{array}{ccc} m+m_{11} &{} m_{12} &{} m_{13} \\ m_{21} &{} m+m_{22} &{} m_{23} \\ m_{31} &{} m_{32} &{} I_z+m_{33} \\ \end{array} \right] \left\{ \ \begin{array}{cc} \dot{U}_1 \\ \dot{U}_2 \\ \dot{U}_3 \\ \end{array} \right\} + \left[ \begin{array}{ccc} \dot{m}_{11} &{} \dot{m}_{12} &{} \dot{m}_{13} \\ \dot{m}_{21} &{} \dot{m}_{22} &{} \dot{m}_{23} \\ \dot{m}_{31} &{} \dot{m}_{32} &{} \dot{m}_{33} \\ \end{array} \right] \left\{ \ \begin{array}{cc} U_1 \\ U_2 \\ U_3 \\ \end{array} \right\} \nonumber \\{} & {} + \left[ \begin{array}{ccc} -(m+m_{22})-D_{23}^{(1)} &{} -m_{21}-D_{31}^{(1)} &{} -D_{12}^{(1)} \\ m_{12}-D_{23}^{(2)} &{} m+m_{11}-D_{31}^{(2)} &{} -D_{12}^{(2)} \\ -m_{13}-D_{23}^{(3)} &{} m_{23}-D_{31}^{(3)} &{} m_{22}-m_{11}-D_{12}^{(3)} \\ \end{array} \right] \left\{ \ \begin{array}{cc} U_2U_3 \\ U_3U_1 \\ U_1U_2 \\ \end{array} \right\} \nonumber \\{} & {} + \left[ \begin{array}{ccc} -D_{11}^{(1)}/2 &{} -D_{22}^{(1)}/2 &{} -m_{23}-D_{33}^{(1)}/2 \\ -D_{11}^{(2)}/2 &{} -D_{22}^{(2)}/2 &{} m_{13}-D_{33}^{(2)}/2 \\ m_{21}-D_{11}^{(3)}/2 &{} -m_{12}-D_{22}^{(3)}/2 &{} -D_{33}^{(3)}/2 \\ \end{array} \right] \left\{ \ \begin{array}{cc} {U}_1^2 \\ {U}_2^2 \\ {U}_3^2 \\ \end{array} \right\} =\left\{ \ \begin{array}{cc} F_{V1} + F_{E1} \\ F_{V2} + F_{E2} \\ F_{V3} + F_{E3} \\ \end{array} \right\} \end{aligned}$$
(30)

This equation is the equation of motion with the added mass expressed explicitly for ship maneuvering in the proximity of the bank [5]. All the coupling terms explicitly appear and change depending on the positional relationship between the ship and bank, owing to the asymmetric flow field around the ship caused by the presence of the bank. In addition, the terms with respect to the time derivative of the added mass exist in the same form as the motion damping coefficients.

For reference, if there are no banks, considering the symmetry of the ship, the time derivative terms of the added mass and the \(D_{ik}^{(j)}\) terms are zero, and the following equation is obtained.

$$\begin{aligned} \left. \begin{array}{lll} &{} &{}(m+m_{11})\dot{U}_1 - (m+m_{22})U_2U_3-m_{23}U_3^2= F_{V1} + F_{E1} \\[5pt] &{} &{} (m+m_{22})\dot{U}_2 + m_{23}\dot{U}_3 + (m+m_{11})U_3U_1 = F_{V2} + F_{E2} \\[5pt] &{} &{} (I_z+m_{33})\dot{U}_3 + m_{23}\dot{U}_2 +(m_{22}-m_{11})U_1U_2 + m_{23}U_3U_1= F_{V3} + F_{E3} \end{array} \right\} \end{aligned}$$
(31)

This equation agrees with the equation of motion derived by Inoue[8].

2.2 Linearized equation of motion in a canal

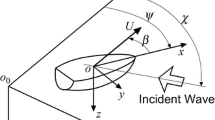
We apply the obtained equation of motion (30) to the problem of the maneuvering motion of a ship navigating in a uniform canal. Figure 1 shows the coordinate systems used. The origin o in the ship fixed coordinate system is matched with the center of gravity of the ship G. The ship is assumed to be navigating near the center line of the canal. W is the canal width. The \(x_S\) axis in the space fixed coordinate system is taken along the center line. The \(z_S\) axis points vertically downward, and the \(y_S\) axis is taken as lateral direction. \(\eta\) is the lateral deviation from the center line of the canal (\(x_S\) axis), and \(\psi\) is the heading angle of the ship. \(\delta\) is rudder angle. Ship speed U is defined as \(U=\sqrt{u^2+v^2}\). Hull drift angle \(\beta\) is defined as \(\beta =-\tan ^{-1}(v/u)\).

Fig. 1
figure 1

Coordinate system of a ship in a canal

Full size image

We consider the maneuvering motion of a ship navigating near the centerline of a canal (\(\eta =0\)). The added mass \(m_{ik}\) and \(D_{ik}^{(j)}\) change when the ship shifts \(\eta\) from the centerline or changes the course \(\psi\). Assuming that \(\eta\) and \(\psi\) are sufficiently small, \(m_{ik}\) and \(D_{ik}^{(j)}\) can be expressed by Taylor’s expansion as follows.

$$\begin{aligned} m_{ik}= & {} m_{ik0}+m_{ik\eta }\eta + m_{ik\psi }\psi + O\left( \eta ^2, \eta \psi , \psi ^2\right) \end{aligned}$$
(32)
$$\begin{aligned} D_{ik}^{(j)}= & {} D_{ik0}^{(j)}+D_{ik\eta }^{(j)}\eta +D_{ik\psi }^{(j)}\psi + O\left( \eta ^2, \eta \psi , \psi ^2\right) \end{aligned}$$
(33)

The subscripts \(\eta\) and \(\psi\) represent the partial derivatives. The time derivative of \(m_{ik}\) is expressed as

$$\begin{aligned} \dot{m}_{ik}= & {} m_{ik\eta }\dot{\eta } + m_{ik\psi }\dot{\psi } \end{aligned}$$
(34)
$$\begin{aligned}= & {} m_{ik\eta }(U\psi +v) + m_{ik\psi }r \end{aligned}$$
(35)

When the maneuvering motion (v, r) of the ship is small, \(F_V\) and \(F_E\) are expressed as follows.

$$\begin{aligned} F_{V2}= & {} Y_{v0} v + Y_{r0} r, \ \ F_{V3}=N_{v0} v + N_{r0} r \end{aligned}$$
(36)
$$\begin{aligned} F_{E2}= & {} Y_{\delta } \delta , \ \ F_{E3}=N_{\delta } \delta \end{aligned}$$
(37)

where \(Y_{v0}\), \(Y_{r0}\), \(N_{v0}\), and \(N_{r0}\) are the hydrodynamic derivatives caused by the fluid viscosity. We consider the rudder forces as \(F_{E2}\) and \(F_{E3}\). Substituting these into Eq. (30) gives the equation of motion for sway and yaw.

$$\begin{aligned} \left( m+m_{220}\right) \dot{v} + m_{230}\dot{r}= & {} Y_v v + \left( Y_r-mU\right) r + Y_{\psi } \psi + Y_{\eta } \eta + Y_{\delta } \delta \end{aligned}$$
(38)
$$\begin{aligned} m_{320}\dot{v}+(I_z+m_{330})\dot{r}= & {} N_v v + N_r r +N_{\psi } \psi + N_{\eta } \eta + N_{\delta } \delta \end{aligned}$$
(39)

where

$$\begin{aligned} \left. \begin{array}{lll} Y_v = Y_{v0} - m_{21\eta }U \\ Y_r =Y_{r0} - \left( m_{110}+m_{21\psi }\right) U \\ Y_{\psi } =\left[ -m_{21\eta } + D_{11\psi }^{(2)}/2\right] U^2 \\ Y_{\eta } = \left[ D_{11\eta }^{(2)}/2\right] U^2 \\ N_v = N_{v0} - \left( m_{220}-m_{110}+m_{31\eta }\right) U \\ N_r = N_{r0} - \left( m_{230}+m_{31\psi }\right) U \\ N_{\psi } = \left[ -m_{21\psi }-m_{31\eta } + D_{11\psi }^{(3)}/2\right] U^2 \\ N_{\eta } = \left[ -m_{21\eta }+D_{11\eta }^{(3)}/2\right] U^2 \end{array} \right\} \end{aligned}$$
(40)

From Eq. (40), the ship navigating in the canal has the potential-based derivatives, which can be calculated by partial differentiation of added mass (\(m_{ji}\)) and \(D_{ik}^{(j)}\) with respect to \(\eta\) and \(\psi\) in addition to the added mass and the derivatives due to fluid viscosity (\(Y_{v0}\), \(Y_{r0}\), \(N_{v0}\), \(N_{r0}\)).

By non-dimensionalizing Eqs. (38) and (39), the following equations are obtained.

$$\begin{aligned} \left( m'+m_{220}'\right) \dot{v}' + m_{230}'\dot{r}'= & {} Y_v' v' + \left( Y_r'-m'\right) r' + Y_{\psi }' \psi + Y_{\eta }' \eta ' + Y_{\delta }' \delta \end{aligned}$$
(41)
$$\begin{aligned} m_{320}'\dot{v}'+\left( I_z'+m_{330}'\right) \dot{r}'= & {} N_v' v' + N_r' r' +N_{\psi }' \psi + N_{\eta }' \eta ' + N_{\delta }' \delta \end{aligned}$$
(42)

The terms with respect to \(Y'_{\psi }\) and \(N'_{\psi }\) appear in the equation of motion, although these disappear in the existing studies [1,2,3]. These terms cannot be neglected theoretically. Notably, non-dimensionalization is performed according to the following equations.

$$\begin{aligned}{} & {} m', m_{220}'= \frac{m, m_{220}}{(1/2) \rho L^2d}, \ \ m_{230}', m_{320}'= \frac{m_{230}, m_{320}}{(1/2) \rho L^3d}, \ \ I_{z}', m_{330}' = \frac{I_{z}, m_{330}}{(1/2) \rho L^4d} \\{} & {} Y_v' = \frac{Y_v}{(1/2) \rho L\textrm{d}U}, \ \ Y_r' = \frac{Y_r}{(1/2) \rho L^2dU}, \ \ Y_{\psi }' = \frac{Y_{\psi }}{(1/2) \rho LdU^2}, \ \ Y_{\eta }' = \frac{Y_{\eta }}{(1/2) \rho \textrm{d}U^2} \\{} & {} N_v' = \frac{N_v}{(1/2) \rho L^2\textrm{d}U}, \ \ N_r' = \frac{N_v}{(1/2) \rho L^3\textrm{d}U}, \ \ N_{\psi }' = \frac{N_{\psi }}{(1/2) \rho L^2\textrm{d}U^2}, \ \ N_{\eta }' = \frac{N_{\eta }}{(1/2) \rho L\textrm{d}U^2} \\{} & {} Y_{\delta }' = \frac{Y_{\delta }}{(1/2) \rho L\textrm{d}U^2}, \ \ N_{\delta }' = \frac{N_{\delta }}{(1/2) \rho L^2\textrm{d}U^2}, \ \ v' = \frac{v}{U}, \ \ r' = \frac{rL}{U}, \ \ \eta ' = \frac{\eta }{L} \end{aligned}$$

2.3 Determining the linear hydrodynamic derivatives in a canal by tank tests

We consider a method for determining the linear hydrodynamic derivatives and the added mass of a ship in a canal by tank tests. As shown by Fujino [1] and Eda [2], the derivatives and added mass of the ship have been measured by oblique towing tests and planar motion mechanism (PMM) tests [9] in the canal. With reference to them, all the linear derivatives, including \(Y'_\psi\) and \(N'_\psi\), and added mass are experimentally obtained. Here, we consider the following four tests.

  • Straight towing test with lateral deviation

  • Oblique towing test

  • Pure sway test

  • Pure yaw test

The straight towing test with lateral deviation and the oblique towing test are called static tests. The pure sway and pure yaw tests are a type of the forced oscillation tests and are called the PMM tests.

2.3.1 Straight towing test with lateral deviation

In the test, the ship model is towed straight with a lateral deviation \(\eta\) from the center line of the canal; thus \(\dot{v}=\dot{r}=v=r=\psi =0\) holds. Therefore, the measured lateral force \(Y_{mea}\) and yaw moment \(N_{mea}\) are represented in Eqs.(38) and (39) as follows:

$$\begin{aligned} Y_{mea} = Y_{\eta }\eta , \ \ \ N_{mea}= N_{\eta }\eta \end{aligned}$$
(43)

By non-dimensionalized these,

$$\begin{aligned} Y_{mea}' = Y_{\eta }'\eta ', \ \ \ N_{mea}'= N_{\eta }'\eta ' \end{aligned}$$
(44)

are obtained. \(Y_{\eta }'\) and \(N_{\eta }'\) can be obtained by this test.

2.3.2 Oblique towing test

This is a straight towing test with an oblique angle (hull drift angle) \(\beta (\simeq -v')\) on the center line of the canal. Since \(\dot{v}=\dot{r}=r=\eta =0\) and \(\psi \simeq -v'\), the measured lateral force \(Y_{mea}\) and yaw moment \(N_{mea}\) are represented as

$$\begin{aligned} Y_{mea} = \left( Y_v - Y_{\psi }/U\right) v, \ \ \ N_{mea} = \left( N_v - N_{\psi }/U\right) v \end{aligned}$$
(45)

By non-dimensionalizing these,

$$\begin{aligned} Y_{mea}' = \left( Y_v' - Y_{\psi }'\right) v', \ \ \ N_{mea}' = \left( N_v' - N_{\psi }'\right) v' \end{aligned}$$
(46)

are obtained. Thus, the measured results (\(Y_{mea}'\), \(N_{mea}'\)) include not only the terms for \(Y_v'\) and \(N_v'\) but also the terms for \(Y_{\psi }'\) and \(N_{\psi }'\). However, since \(Y_v'\) and \(N_v'\) are separately obtained from the pure sway test described below, \(Y_{\psi }'\) and \(N_{\psi }'\) are known.

2.3.3 Pure sway test

We consider that the ship model is forced to laterally move with the frequency \(\omega\) while keeping \(\dot{r}=r=\psi =0\). The lateral displacement \(\eta\) is expressed as

$$\begin{aligned} \eta = -y_{\textrm{amp}} {\textrm{Re}}\left[ i \exp (i\omega t)\right] \end{aligned}$$
(47)

where \(i=\sqrt{-1}\). \(y_{\textrm{amp}}\) is the amplitude of the lateral displacement. By differentiating \(\eta\) with respect to time t,

$$\begin{aligned} v= & {} y_{\textrm{amp}}\omega {\textrm{Re}}\left[ \exp (i\omega t) \right] , \ \ \dot{v} = y_{\textrm{amp}} \omega ^2 {\textrm{Re}}\left[ i \exp (i\omega t)\right] \end{aligned}$$

are obtained. Here, the measured results are represented as \(Y_{mea}={\textrm{Re}}[\hat{Y}_{ps}\exp (i\omega t)]\), and \(N_{mea}={\textrm{Re}}[\hat{N}_{ps}\exp (i\omega t)]\). Substituting these into Eqs. (38) and (39) yields the following equations.

$$\begin{aligned} {\textrm{Re}}\left[ \hat{Y}_{ps}\right]= & {} y_{\textrm{amp}}Y_{v}\omega \end{aligned}$$
(48)
$$\begin{aligned} {\textrm{Im}}\left[ \hat{Y}_{ps}\right]= & {} y_{\textrm{amp}} \left[ Y_{\eta } + (m+m_{220})\omega ^2 \right] \end{aligned}$$
(49)
$$\begin{aligned} {\textrm{Re}}\left[ \hat{N}_{ps}\right]= & {} y_{\textrm{amp}} N_{v}\omega \end{aligned}$$
(50)
$$\begin{aligned} {\textrm{Im}}\left[ \hat{N}_{ps}\right]= & {} y_{\textrm{amp}}\left[ N_{\eta } + m_{320}\omega ^2 \right] \end{aligned}$$
(51)

By non-dimensionalizing these,

$$\begin{aligned} {\textrm{Re}}\left[ \hat{Y}'_{ps}\right]= & {} y_{\textrm{amp}}'Y_{v}'\omega ' \end{aligned}$$
(52)
$$\begin{aligned} {\textrm{Im}}\left[ \hat{Y}'_{ps}\right]= & {} y_{\textrm{amp}}' \left[ Y_{\eta }' + (m'+m_{220}')\omega '^2 \right] \end{aligned}$$
(53)
$$\begin{aligned} {\textrm{Re}}\left[ \hat{N}'_{ps}\right]= & {} y_{\textrm{amp}}' N_{v}'\omega ' \end{aligned}$$
(54)
$$\begin{aligned} {\textrm{Im}}\left[ \hat{N}'_{ps}\right]= & {} y_{\textrm{amp}}' \left[ N_{\eta }' + m_{320}'\omega '^2 \right] \end{aligned}$$
(55)

are obtained. \(\omega '=\omega L/U\). \(Y_v'\) and \(N_v'\) are obtained from Eqs. (52) and (54), respectively. When \(Y_{\eta }'\) and \(N_{\eta }'\) are known, \(m_{220}'\) and \(m_{320}'\) are obtained from Eqs. (53) and (55), respectively.

2.3.4 Pure yaw test

We consider that the ship model is forced to move with the frequency \(\omega\) for \(\eta\) and \(\psi\) as follows.

$$\begin{aligned} \eta= & {} -y_{\textrm{amp}} {\textrm{Re}}[ i\exp (i\omega t)] \end{aligned}$$
(56)
$$\begin{aligned} \psi= & {} \frac{y_{\textrm{amp}}\omega }{U}{\textrm{Re}}[\exp (i\omega t)] \end{aligned}$$
(57)

Then,

$$\begin{aligned} v= & {} y_{\textrm{amp}}\omega {\textrm{Re}}[\exp (i\omega t)] - U \psi = 0 \end{aligned}$$
(58)

holds, such that the lateral velocity v is zero. On the other hand, by differentiating \(\psi\) with respect to time,

$$\begin{aligned} r= & {} \frac{y_{\textrm{amp}}\omega ^2}{U} {\textrm{Re}}[i\exp (i\omega t)], \ \ \dot{r} = -\frac{y_{amp}\omega ^3}{U} {\textrm{Re}}[ \exp (i\omega t)] \end{aligned}$$

are obtained. Here, the measured results are represented as \(Y_{mea}={\textrm{Re}}[\hat{Y}_{py}\exp (i\omega t)]\), and \(N_{mea}={\textrm{Re}}[\hat{N}_{py}\exp (i\omega t)]\). Substituting these into Eqs.(38) and (39) yields the following equations.

$$\begin{aligned} {\textrm{Re}}[\hat{Y}_{py}]= & {} y_{\textrm{amp}}\frac{\omega }{U} \left[ Y_{\psi }+m_{230}\omega ^2 \right] \end{aligned}$$
(59)
$$\begin{aligned} {\textrm{Im}}[\hat{Y}_{py}]= & {} y_{\textrm{amp}}\left[ Y_{\eta } - (Y_r-mU) \frac{\omega ^2}{U} \right] \end{aligned}$$
(60)
$$\begin{aligned} {\textrm{Re}}[\hat{N}_{py}]= & {} y_{\textrm{amp}} \frac{\omega }{U} \left[ N_{\psi }+(I_z+m_{330})\omega ^2 \right] \end{aligned}$$
(61)
$$\begin{aligned} {\textrm{Im}}[\hat{N}_{py}]= & {} y_{\textrm{amp}}\left[ N_{\eta } - N_r \frac{\omega ^2}{U} \right] \end{aligned}$$
(62)

By non-dimensionalized these,

$$\begin{aligned} {\textrm{Re}}[\hat{Y}'_{py}]= & {} y_{\textrm{amp}}'\omega '\left[ Y_{\psi }'+m_{230}'\omega '^2 \right] \end{aligned}$$
(63)
$$\begin{aligned} {\textrm{Im}}[\hat{Y}'_{py}]= & {} y_{\textrm{amp}}'\left[ Y_{\eta }' - (Y_r'-m') \omega '^2 \right] \end{aligned}$$
(64)
$$\begin{aligned} {\textrm{Re}}[\hat{N}'_{py}]= & {} y_{\textrm{amp}}' \omega ' \left[ N_{\psi }'+(I_z'+m_{330}')\omega '^2 \right] \end{aligned}$$
(65)
$$\begin{aligned} {\textrm{Im}}[\hat{N}'_{py}]= & {} y_{\textrm{amp}}'\left[ N_{\eta }' - N_r' \omega '^2 \right] \end{aligned}$$
(66)

are obtained. \(Y_r'\) and \(N_r'\) are obtained from Eqs.(64) and (66) when \(Y_{\eta }'\) and \(N_{\eta }'\) are known, respectively. Further, when \(Y_{\psi }'\) and \(N_{\psi }'\) are known, \(m_{230}'\) and \(m_{330}'\) are obtained from Eqs.(63) and (65), respectively.

3 Measurement of hydrodynamic derivatives and added mass coefficients in a canal

Using the formulas described in Section 2.3, all linear hydrodynamic derivatives and added mass are determined by captive model tests.

3.1 Target ship and canal

In this study, we targeted a mega container ship (MCS) similar to the ship that ran aground in the Suez Canal in March 2021. All the principal particulars and hull form of this ship are based on the authors’ estimations. In the captive model tests, a temporary floor-typed shallow water facility (false bottom) was used at the Hiroshima University towing tank (length of 100 m, width of 8 m, and maximum depth of 3.5 m), and a uniform canal model (length of 33 m) was placed on the false bottom. Figure 2 shows the overview of the canal model, which is made of transparent urethane plates.

Fig. 2
figure 2

Overview of a canal model on the false bottom in Hiroshima University towing tank

Full size image

Table 1 lists the principal particulars of the full-scale ship and the ship model of MCS. The scale ratio of the model is 1/128.125. In the table, L is length between perpendiculars, B is breadth, d is draft, S is wetted surface area, \(\nabla\) is displacement volume, \(C_{b}\) is block coefficient, and \(x_{G}\) is the longitudinal position of the center of gravity. The ship has bilge keels that measure approximately 116 m in length when scaled to full size. Figure 3 shows a body plan with stern and stem profiles of MCS.

Table 1 Principal particulars of a mega container ship
Full size table
Fig. 3
figure 3

Body plan and profiles of a subject ship (MCS)

Full size image

Table 2 shows the principal particulars of rudder and propeller of MCS. In the table, \(H_{R}\) is the rudder height, \(B_{R}\) is the average chord length, and \(A_{R}\) is the rudder area including the rudder horn. \(D_{p}\) is the propeller diameter, p is the pitch ratio, and Z is the number of propeller blades.

Table 2 Principal particulars of rudder and propeller of MCS
Full size table

It should be noted that free running tests of turning and zig-zag maneuvers in deep water for the target ship have been conducted before the captive tests, and we have confirmed no problems of the ship maneuverability.

The captive tests were conducted by changing the ratio of the water depth to the draft h/d, as 1.90, 1.59, and 1.30. The water depth south of the Suez Canal where the grounding accident occurred is \(h=25\)m and corresponds to \(h/d=1.59\). Figure 4 shows the cross-sectional shape of the canal at each water depth. The cross-sectional shape was trapezoidal with a slope of 1:3. When \(h/d=1.59\), the width at the water line is \(W=2.115\)m and the water depth is \(h=0.195\)m.

Fig. 4
figure 4

Cross section of a canal (full-scale)

Full size image

3.2 Outline of captive model tests

In the captive tests, the speed of the ship model was set U=0.393 m/s (\(F_{n}\)=0.072 where \(F_n\) is the Froude number based on L) regardless of the water depth. The speed of the ship of approximately 8.6 knots corresponds to the standard navigation speed in the Suez Canal. The propeller revolution \(n_p\) was set as the self-propulsion condition (model point) at each water depth. Table 3 shows the propeller revolutions at each water depth.

Table 3 Propeller revolutions at model point in captive model tests
Full size table

The details of the test conditions are as follows.

  • Straight towing test with lateral deviation: The lateral deviation \(\eta\) was changed as 0, ±0.078, ±0.156, ±0.234, ±0.312 m.

  • Oblique towing test: The hull drift angle \(\beta\) was changed as 0\(^\circ\), \(\pm 3^\circ\), \(\pm 6^\circ\), \(\pm 9^\circ\), and \(\pm 12^\circ\). However, there was a risk of contact between the ship hull and sea bottom in \(h/d=1.3\) due to the bow sinkage; thus, the test was not performed at \(\pm 12^\circ\).

  • Pure sway and pure yaw tests: The tests were conducted with the combination of the periods and amplitudes of the forced oscillation shown in Table 4. The period \(T(=2\pi /\omega )\) was changed as T=35.3, 17.7, and 11.8 s. The analysis was performed using the measurement data for three and five cycles when T was 17.7 and 11.8 s, respectively. When T was 35.3 s, one period measurement data was used for the analysis.

Rudder angle was zero for all the tests.

Table 4 Test condition of the combination of periods and amplitudes for PMM tests
Full size table

In the tests, surge force (X), lateral force (Y), and yaw moment (N) acting on the ship model were measured, although the surge force is not mentioned in this study. The heel was fixed, and the hull sinkage and trim were free. They were measured using a three-component dynamo-meter installed on the midship of the ship model. The forces and moment measured at the midship include the inertial forces, but the inertial forces were properly removed. The lateral force Y and yaw moment N measured at the midship are distinguished by adding a subscript m, such as \(Y_m\) and \(N_m\), respectively.

3.3 Test results

3.3.1 Results of straight towing test with lateral deviation

Figure 5 illustrates the lateral force coefficient \(Y_m'\) and the yaw moment coefficient \(N_m'\) obtained in the straight towing tests with the lateral deviation. The measured values are non-dimensionalized based on \(\rho\), L, d, and U. The inclinations of \(Y_m'\) and \(N_m'\) with respect to \(\eta '(=\eta /L)\) are the linear derivatives (\(Y'_{m\eta }\), \(N'_{m\eta }\)). The fitting straight lines are also shown in the figure. The absolute value of \(Y_m'\) increases as \(\eta '\) increases, and this tendency becomes more significant as the water depth becomes shallower. This is known as the bank suction force. \(N_m'\) negatively increases as \(\eta '\) grows. This tendency becomes more significant as the water depth becomes shallower, especially when h/d=1.3, the absolute value of \(N_m'\) greatly increases. This is well known as the bow-out yaw moment, which is the direction in which the bow leaves the bank. \(Y_m'\) and \(N_m'\) linearly change with respect to \(\eta '\). The obtained \(Y'_{m\eta }\) and \(N'_{m\eta }\) are shown in Table 5.

Fig. 5
figure 5

Comparison of lateral force and yaw moment acting on the ship during straight towing tests with lateral deviation in h/d=1.9, 1.59, and 1.3

Full size image
Table 5 Hydrodynamic derivatives with respect to lateral deviation obtained by straight towing test in h/d=1.9, 1.59, and 1.3
Full size table

3.3.2 Oblique towing test results

Figure 6 illustrates the lateral force coefficient \(Y_m'\) and the yaw moment coefficient \(N_m'\) obtained from the oblique towing tests. In the figure, a fitting curve obtained as the 1st and 3rd order polynomial functions of the hull drift angle \(\beta\) is plotted.

\(Y'_{mv}-Y'_{m\psi }\) and \(N'_{mv}-N'_{m\psi }\) are obtained by taking the slope of the fitting curve at the origin with respect to the non-dimensional lateral velocity \(v'(=v/U\simeq -\beta )\). The absolute value of \(Y_m'\) shows a remarkable increase from h/d=1.59 to 1.3. This trend is the same for \(N_m'\). Since the cross-section of the target canal in this study is trapezoidal, the width at the water level decreases as the water depth becomes shallower. Therefore, the canal becomes narrower with decrease of the water depth, and the influence of the canal wall is significant. Table 6 lists the obtained derivatives. \(Y'^*_{mvvv}\) and \(N'^*_{mvvv}\) are the cubic terms of \(v'\).

Fig. 6
figure 6

Comparison of lateral force and yaw moment acting on the ship during oblique towing tests in h/d=1.9, 1.59, and 1.3

Full size image
Table 6 Hydrodynamic derivatives obtained by oblique towing tests in h/d=1.9, 1.59, and 1.3
Full size table

3.3.3 Pure sway test results

Figure  7 shows the results of Im\([\hat{Y'}_{ps}]^*\), Im\([\hat{N'}_{ps}]^*\), Re\([\hat{Y'}_{ps}]\), and Re\([\hat{N'}_{ps}]\) in h/d=1.59, which were obtained by the pure sway tests. Im\([\hat{Y'}_{ps}]^*\) and Im\([\hat{N'}_{ps}]^*\) are defined as

$$\begin{aligned} \left. \begin{array}{lll} {\textrm{Im}}\left[ \hat{Y}'_{ps}\right] ^*=\hspace{-3mm}{\textrm{Im}}\left[ \hat{Y}'_{ps}\right] -y_{\textrm{amp}}'Y_{m\eta }'\\ {\textrm{Im}}\left[ \hat{N}'_{ps}\right] ^*={\textrm{Im}}\left[ \hat{N}'_{ps}\right] -y_{\textrm{amp}}'N_{m\eta }' \end{array} \right\} \end{aligned}$$
(67)

In the graph, the horizontal axis is \(y'_{\textrm{amp}}\omega '^2\) or \(y'_{\textrm{amp}}\omega '\). \(m'+m'_{220}\), \(m'_{320}\), \(Y'_{mv}\), and \(N'_{mv }\) are obtained by taking the slope of the graph passing through the origin for the measurement results. \(Y'_{m\psi }\) and \(N'_{m \psi }\) are determined when \(Y'_{mv}\) and \(N'_{mv}\) are obtained. They have different values depending on T.

Fig. 7
figure 7

Analysis results and fitting lines of lateral force and yaw moment with various frequencies obtained by the pure sway tests in h/d=1.59

Full size image

3.3.4 Pure yaw test results

Figure  8 shows the results of Re\([\hat{Y'}_{py}]^*\), Re\([\hat{N'}_{py}]^*\), Im\([\hat{Y'}_{py}]^*\), and Im\([\hat{N'}_{py}]^*\), which are defined as follows.

$$\begin{aligned} \left. \begin{array}{lll} {\textrm{Re}}\left[ \hat{Y}'_{py}\right] ^*={\textrm{Re}}\left[ \hat{Y}'_{py}\right] -y_{\textrm{amp}}'Y_{m\psi }'\omega '\\ {\textrm{Re}}\left[ \hat{N}'_{py}\right] ^*={\textrm{Re}}\left[ \hat{N}'_{py}\right] -y_{\textrm{amp}}'N_{m\psi }'\omega '\\ {\textrm{Im}}\left[ \hat{Y}'_{py}\right] ^*={\textrm{Im}}\left[ \hat{Y}'_{py}\right] -y_{\textrm{amp}}'Y_{m\eta }'\\ {\textrm{Im}}\left[ \hat{N}'_{py}\right] ^*={\textrm{Im}}\left[ \hat{N}'_{py}\right] -y_{\textrm{amp}}'N_{m\eta }' \end{array} \right\} \end{aligned}$$
(68)

In the graph, the horizontal axis is \(y'_{\textrm{amp}}\omega '^3\) or \(y'_{\textrm{amp}}\omega '^2\). \(m'_{230}\), \(I_{z}'+m'_{330}\), \(Y'_{mr}-m'\), and \(N'_{mr}\) are obtained by taking the slope of the graph passing through the origin for the measurement results. To obtain \(m'_{330}\), the moment of inertia \(I_z'\) for yaw of the ship model is required. Here, the moment of inertia for pitch of the ship model was measured and this was regarded as \(I_z'\). \(I_z'\) was 0.0135. \({\textrm{Im}}[\hat{Y}'_{py}]^*\) was remarkably scattered when \(T=35.3\)s. In addition, \({\textrm{Re}}[\hat{Y}'_{py}]^*\) has different slopes depending on T. The difference in slope appears as a change of \(m'_{230}\)-value.

Fig. 8
figure 8

Analysis results and fitting lines of lateral force and yaw moment with various frequencies obtained by pure yaw tests in h/d=1.59

Full size image

3.4 Summary of hydrodynamic derivatives and added mass coefficients

Since the derivatives obtained in the tank tests are midship-based, they were converted to the center-of-gravity-based. The conversion formulas are expressed as follows.

$$\begin{aligned} \left. \begin{array}{lll} Y_v' = Y_{mv}' \\ Y_r' = Y_{mr}' - x_G'Y_{mv}' \\ Y_{\psi }' = Y_{m\psi }' \\ Y_{\eta }' = Y_{m\eta }' \\ N_v' = N_{mv}'+ x_G'Y_{mv}' \\ N_r' = N_{mr}'+ x_G'Y_{mr}' - x_G'N_{mv}'- x_G'^2Y_{mv}' \\ N_{\psi }' = N_{m\psi }'+ x_G'Y_{m\psi }' \\ N_{\eta }' = N_{m\eta }'+ x_G'Y_{m\eta }' \end{array} \right\} \end{aligned}$$
(69)

where \(x_G'=x_G/L\). Table 7 lists the hydrodynamic derivatives with respect to lateral deviation (\(Y_\eta '\), \(N_\eta '\)) in h/d=1.9, 1.59, and 1.3. \(Y_\eta '\) and \(N_\eta '\) are obtained by the static test; thus, they are constant regardless of the frequency. All the derivatives except \(Y_\eta '\) and \(N_\eta '\), and added mass coefficients in h/d=1.9, 1.59, and 1.3 are shown in Tables 8, 9, and 10. Additionally, Figs. 9 and 10 show the comparison of the added mass coefficients and hydrodynamic derivatives, respectively. For the graphs, the horizontal axis is non-dimensionalized frequency \(\omega \sqrt{L/g}\) at the PMM tests. \(m_{220}'\) decreases as the frequency decreases. \(m_{320}'\) is a positive value and tends to decrease as the frequency increases. On the other hand, \(m_{230}'\) greatly varies with the frequency and can be negative. According to the potential theory, \(m_{230}'\) should match \(m_{320}'\)[10], and it does not hold. \(m_{330}'\) changes significantly when the frequency is small. In case of the lowest frequency (\(\omega \sqrt{L/g}=0.099\)), it is observed that the added mass and the derivative coefficients significantly change. In the analysis at \(\omega \sqrt{L/g}=0.099\), only one cycle of the measurement data can be used; thus, there may be a problem with the reliability of the analysis results. \(Y_v'\), \(Y_r'\), \(N_v'\), and \(N_r'\) change with the frequency, but the change is not sufficiently large. \(Y_{\psi }'\) and \(N_{\psi }'\) remarkably change with the frequency.

Table 7 Hydrodynamic derivatives with respect to lateral deviation in h/d=1.9, 1.59, and 1.3
Full size table
Table 8 Added mass coefficients and linear hydrodynamic derivatives obtained by the captive model tests in \(h/d=1.9\)
Full size table
Table 9 Added mass coefficients and linear hydrodynamic derivatives obtained by the captive model tests in \(h/d=1.59\)
Full size table
Table 10 Added mass coefficients and linear hydrodynamic derivatives obtained by the captive model tests in \(h/d=1.3\)
Full size table
Fig. 9
figure 9

Comparison of added mass coefficients versus forced frequency

Full size image
Fig. 10
figure 10

Comparison of hydrodynamic derivatives versus forced frequency

Full size image

Figure 11 illustrates the relationship between added mass coefficients, derivatives of the lateral force, and the yaw moment with water depth (h/d) at T=17.7 s (\(\omega \sqrt{L/g}=0.197\)). In the graph of the added mass coefficients, the calculation results are also shown based on the potential theory described in Section 2. The details of the added mass calculation are described in the appendix at the end of the paper together with the calculation results on the changes in the added mass when the ship approaches the canal wall. Except for \(m_{230}'\), all added mass coefficients and the derivatives increase in absolute value as the water depth becomes shallower. The calculation results of \(m_{220}'\), \(m_{320}'\), and \(m_{330}'\) by the potential theory show the same tendency as that of the experimental results, but it is quantitatively smaller. The reason is that the calculation does not include the effect of the ship’s attitude change and the free surface. \(Y_{\psi }'\) is positive and \(N_{\psi }'\) is negative. When the ship turns to the starboard and the bow approaches the canal wall, a lateral force acts in the direction of being attracted to the wall, and a yaw moment acts to push the bow away from the wall. This is the same property as \(Y_{\eta }'\) and \(N_{\eta }'\). However, the absolute values of \(Y_{\psi }'\) and \(N_{\psi }'\) are smaller than \(Y_{\eta }'\) and \(N_{\eta }'\), respectively, and are approximately the same order of magnitude as \(Y_r'\) and \(N_r'\), respectively. Thus, \(Y_{\psi }'\) and \(N_{\psi }'\) are not negligible.

Fig. 11
figure 11

Comparison of added mass coefficients, Y-derivatives, and N-derivatives versus h/d

Full size image

4 Course stability of a ship in a canal

Using the obtained added mass coefficients and hydrodynamic derivatives, we investigated the course stability of the ship in the canal. Particularly, we examined the effect of consideration of the derivatives with respect to heading angle (\(Y'_{\psi }\), \(N'_{\psi }\)) on the course stability.

4.1 Course stability criteria in a canal

We considered the ship navigating the center of the canal using autopilot. It is assumed that the rudder angle \(\delta\) is calculated by \(\delta =-G_1\psi -G_2r'\) under a PD control, where \(G_1\) is the proportional gain and \(G_2\) is the differential gain. Equations (41) and (42) are the equations of motion with coupling of \(\eta '\) and \(\psi\), respectively. By assuming that the solutions of \(\eta '\) and \(\psi\) take the forms \(\eta '=C_1e^{\lambda t}\) and \(\psi =C_2e^{\lambda t}\), respectively, the characteristic equation is obtained as

$$\begin{aligned}{} & {} D_4 \lambda ^4 + D_3\lambda ^3 + D_2\lambda ^2 + D_1 \lambda + D_0 = 0 \end{aligned}$$
(70)

where

$$\begin{aligned} D_4= & {} \left( m'+m_{220}'\right) \left( I_z'+m_{330}'\right) -m_{230}'m_{320}' \end{aligned}$$
(71)
$$\begin{aligned} D_3= & {} N_v'm_{230}'+\left( m_{220}'+Y_r'-Y_{\delta }'G_2\right) m_{320}' -\left( I_z'+m_{330}'\right) Y_v'\nonumber \\{} & {} -\left( m_{320}'+N_r'-N_{\delta }'G_2\right) \left( m'+m_{220}'\right) \end{aligned}$$
(72)
$$\begin{aligned} D_2= & {} m_{230}'N_{\eta }'-\left( m_{220}'+Y_r'-Y_{\delta }'G_2\right) N_v' -\left( Y_v'-Y_{\psi }'+Y_{\delta }'G_1\right) m_{320}'\nonumber \\- & {} \left( I_z'+m_{330}'\right) Y_{\eta }' +\left( m_{320}'+N_r'-N_{\delta }'G_2\right) Y_v'+\left( N_v'- N_{\psi }'+N_{\delta }'G_1\right) \left( m'+m_{220}'\right) \end{aligned}$$
(73)
$$\begin{aligned} D_1= & {} -\left( m_{220}'+Y_r'-Y_{\delta }'G_2\right) N_{\eta }' +\left( Y_v'-Y_{\psi }'+Y_{\delta }'G_1\right) N_v'\nonumber \\{} & {} +\left( m_{320}'+N_r'-N_{\delta }'G_2\right) Y_{\eta }' -\left( N_v'- N_{\psi }'+N_{\delta }'G_1\right) Y_v' \end{aligned}$$
(74)
$$\begin{aligned} D_0= & {} \left( Y_v'-Y_{\psi }'+Y_{\delta }'G_1\right) N_{\eta }'-\left( N_v'-N_{\psi }'+N_{\delta }'G_1\right) Y_{\eta }' \end{aligned}$$
(75)

The characteristic equation is a quartic equation. If the Hurwitz’s criterion shown by the following equation is satisfied, the motion disturbance is attenuated, and the ship can be regarded as course stable.

$$\begin{aligned}{} & {} D_0, D_1, D_2, D_3, D_4 > 0 \end{aligned}$$
(76)
$$\begin{aligned}{} & {} D_5 \equiv D_3D_2D_1 - D_3^2D_0-D_4D_1^2>0 \end{aligned}$$
(77)

4.2 Effect of \(Y'_{\psi }\) and \(N'_{\psi }\) on course stability in a canal

The course stability of the ship was investigated by changing the various steering gains (\(G_{1}\), \(G_{2}\)). The added mass coefficients and hydrodynamic derivatives at T=17.7 s (\(\omega \sqrt{L/g}=0.197\)) were used for the investigation. As the rudder force coefficients \(Y_{\delta }'\) and \(N_{\delta }'\), the values shown in Table 11 were used, which were determined by a captive model test.

Table 11 Rudder force derivatives in h/d=1.9, 1.59, and 1.3
Full size table

We compared the following two cases to investigate the effect of consideration of the \(\psi\)-derivatives (\(Y'_{\psi }\), \(N'_{\psi }\)) on the course stability.

  • Considering the \(\psi\)-derivatives (w/ \(\psi\)-deriv.) Considering the \(\psi\)-derivatives, the hydrodynamic force coefficients (\(Y_H'\), \(N_H'\)) acting on the ship hull are expressed as follows.

    $$\begin{aligned} \left. \begin{array}{lll} Y'_{H} = Y'_{v}v'+Y'_{\psi }\psi +Y'_{\eta }\eta '+Y'_{r}r'\\ N'_{H} = N'_{v}v'+N'_{\psi }\psi +N'_{\eta }\eta '+N'_{r}r' \end{array} \right\} \end{aligned}$$
    (78)

  • Without considering the \(\psi\)-derivatives (w/o \(\psi\)-deriv.) Not considering the \(\psi\)-derivatives, \(Y_H'\) and \(N_H'\) are expressed as

    $$\begin{aligned} \left. \begin{array}{lll} Y'_{H}= Y'^*_{v}v'+Y'_{\eta }\eta '+Y'_{r}r'\\ N'_{H}= N'^*_{v}v'+N'_{\eta }\eta '+N'_{r}r' \end{array} \right\} \end{aligned}$$
    (79)

    where \(Y'^*_{v}\) and \(N'^*_{v}\) are defined as \(Y'^*_{v}=Y_v'-Y_\psi '\) and \(N'^*_{v}=N_v'-N_\psi '\). The derivatives (\(Y'^*_{v}\), \(N'^*_{v}\)) are obtained from oblique towing tests, as shown in Table 12.

Table 12 \(Y'^*_{v}\) and \(N'^*_{v}\) in h/d=1.9, 1.59, and 1.3
Full size table

Figure 12 shows the stable/unstable region for course keeping at h/d=1.9, 1.59, and 1.3. In the graph, the black area indicates an unstable region, and the white region represents a stable region. The horizontal axis is the proportional gain \(G_{1}\), and the vertical axis is the differential gain \(G_{2}\). In general, the white area increases and the ship changes to course stable direction as the water depth becomes shallower. The result without considering the \(\psi\)-derivatives (\(Y_{\psi }'\), \(N_{\psi }'\)) shows a larger unstable region. This is more apparent in h/d=1.3. In summary, the consideration of \(Y'_\psi\) and \(N'_\psi\) changes the ship to the course stable direction. The effect of \(Y'_\psi\) and \(N'_\psi\) on the course stability becomes significant as the water depth becomes shallower.

We investigated where the influence would appear in Eqs. (76) and (77). As the result, the condition of Eq. (77) is not satisfied in the case without \(Y_{\psi }'\) and \(N_{\psi }'\). However, the general mechanism of the course stability changes due to \(\psi\)-derivatives is not well understood because Eq. (77) is complicated. Further investigations targeting various hull forms are required.

Fig. 12
figure 12

Comparison of the stable/unstable region for course keeping with and without consideration of \(\psi\)-derivatives (\(Y'_{\psi }\), \(N'_{\psi }\)) in h/d=1.9, 1.59, and 1.3

Full size image

5 Conclusion

The findings obtained in this study are summarized as follows.

  1. 1.

    Based on the potential theory, a consistent linearized equation of motion was derived when a ship maneuvers near the center line of a canal with a symmetrical cross-section and uniform length. In the new equation of motion, hydrodynamic derivatives for the lateral force and yaw moment with respect to ship heading angle \(\psi\) (\(Y'_\psi\), \(N'_\psi\)) appear, which have not been considered in previous studies.

  2. 2.

    \(Y'_\psi\) and \(N'_\psi\) were measured together with other hydrodynamic derivatives and added mass coefficients by captive tests using a container ship model and a canal model. The measured \(Y'_\psi\) and \(N'_\psi\) have a significant magnitude and become remarkable in shallow water such as \(h/d=1.3\).

  3. 3.

    The course stability criteria for ship in the canal were derived by considering \(Y'_\psi\) and \(N'_\psi\), and the effect of \(Y'_\psi\) and \(N'_\psi\) on the course stability was investigated. The effect of \(Y'_\psi\) and \(N'_\psi\) cannot be neglected when the water depth becomes shallower. In case of the studied container ship, the consideration of \(Y'_\psi\) and \(N'_\psi\) causes the ship to shift to the course stable direction.