Abstract
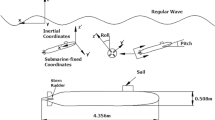
This study developed a numerical prediction method for the emergency ascent of a submarine with flow holes in calm water based on the RANS method, and utilizing sliding and overlapping grids, 6-DOF and DFBI models, and considering interactions between internal and external domains. The proposed approach was verified using numerical simulations, where it was found that the numerical calculation errors were within 10% compared to model submarine ascent test results. The paper then explored further numerically the influence of different positive buoyancies, longitudinal and vertical positions of the center of gravity, and diving depths on the ascent motion of the submarine. The results showed that the greater the positive buoyancy, the shorter the time for the submarine to ascend, but the submarine will be more susceptible to disturbances from the water surface. The more backward the longitudinal position of center of gravity relative to the longitudinal position of center of buoyancy, the greater the submarine head-up during floating, and as a result, the closer to vertical the posture of the submarine when it emerged from underwater, and the greater the peak trim angle. Conversely, when the longitudinal position of the center of gravity shifted forward, the submarine was prone to dangerous head-downs during ascent. The greater the absolute value of the height of the center of gravity, the greater the initial stability of the submarine, and the smaller the effects of water disturbances and damping. In such cases, the heel and trim angles of the submarine will be smaller after it emerges. For the submarine to ascend, the positive buoyancy should take an appropriate value. Consequently, when the longitudinal position of the center of gravity is near the position of the center of buoyancy, the smaller the height of the center of gravity and the diving depth, which is beneficial for the submarine ascent. In conclusion, the proposed numerical method and reported research findings may help to understand the ascent of real submarines.




















Similar content being viewed by others
References
Smallwood DA, Whitcomb L (2003) Adaptive identification of dynamically position underwater robotic vehicles. IEEE Trans Control Syst Technol 11(4):505–515
Watt GD (2002) Estimating the hydrodynamic characteristics of the dorado remote mine hunting vehicle. Research and Development Canada, DRDC Atlantic TM, p 177
Kim J (2002) Estimation of hydrodynamic coefficients for an AUV using nonlinear observers. IEEE J Ocean Eng 27(4):830–840
Watson KP, Webster JS (1993) Prediction of submersible maneuvering performance at high incidence angles. Ocean, pp 289–294
Carrica PM, Ismail F, Hyman M (2013) Turn and zigzag maneuvers of a surface combatant using a URANS approach with dynamic overset grids. J Mar Sci Technol. 18:166–181
Carrica PM, Hosseini HS, Stern F (2012) CFD analysis of broaching for a model surface combatant with explicit simulation of moving rudders and rotating propellers. Comput Fluids 53:117–132
Chase N, Michael T, Carrica PM (2013) Overset simulation of a submarine and propeller in towed self-propelled and maneuvering conditions. Int Shipbuild Prog 60:171–205
Chen QL, Li HW, Zhang SD (2020) Effect of waves on the behavior of emergent buoyantly rising submarines using CFD. Appl Sci 10:1–23
Zhang Z, Guo L, Wei P (2018) Numerical simulation of submarine surfacing motion in regular waves. Iran J Sci Technol Trans Mech Eng 44:359–372
Mojtaba A, Mali T, Paulo A (2018) Marcelo, How does the free surface affect the hydrodynamics of a shallowly submerged submarine? Appl Ocean Res 76:34–50
Kam BD (2019) Improving the hydrodynamic performance of the SUBOFF bare hull model: a CFD approach. A Mech Sin 11:20–34
Francis V, Craig W (2019) Nonlinear control of a subscale submarine in emergency ascent. Ocean Eng 171:646–662
Chang PE, Fang MC (2016) Wave effects on depth control motion of a submarine near the free surface. J Taiwan Soc Naval Arch Mar Eng 35(2):83–92
Lin YH, Tseng SH, Chen YH (2018) The experimental study on maneuvering derivatives of a submerged body SUBOFF by implementing the planar motion mechanism tests. Ocean Eng 170:120–135
Gertler M, Hagen GR (2020) Standard equations of motion for submarine simulation, NSRDC Report 2510. Accessed 25 Nov 2020
Feldman J (2020) Revised standard submarine equations of motion, DTNSRDC/SPD-0393–09. Accessed 25 Nov 2020
Wilcox DC (1998) Turbulence modeling for CFD[R]. DCW Industries Incorporation, La Canada, California
Menter FR (1994) Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J 32(8):1598–1605
Menter FR, Kuntz M, Langtry R (2003) Ten years of industrial experience with the SST turbulence models. Turbul, Heat Mass Trans 4:625–632
Nancy C, Thomas T, Ming S (1989) Geometric characteristics of DARPA SUBOFF models. DTRC/SHD-1298-01 [R]. Ship Hydromechanics Department, UK
Feldman J (1979) DTNSRDC revised standard submarine equations of motion, DTNSRDC Report SPD-0393-09
Acknowledgements
The authors wish to thank the China Special Aircraft Research Institute for providing the test site for experimental work. The authors also acknowledge the Naval University of Engineering for its strong support for the project and enabling the author to conduct experiments and other related investigations.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
About this article
Cite this article
Wei, K., Gao, X., Liu, D. et al. Numerical calculation of six degree of freedom floating motion of submarine with flow holes. J Mar Sci Technol 27, 916–934 (2022). https://doi.org/10.1007/s00773-022-00884-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00773-022-00884-8