Wave-induced steady forces and yaw moment of a ship advancing in oblique waves

Abstract

Wave-induced added resistance, steady sway force, and steady yaw moment, which are of second order in the incident-wave amplitude, are studied for the forward-speed case using the far-field method based on the principles of momentum and energy conservation. The Kochin functions representing ship-disturbance waves, important input data in the far-field method, are evaluated by means of both enhanced unified theory (EUT) and new strip method (NSM) to see the difference due to bow wave diffraction, 3D and forward-speed effects in the final results of second-order steady forces and moment. Special attention is paid on the precise integration method to ensure convergence in semi-infinite integrals in the calculation formulae, introducing no artificial decaying factor unlike conventional strip-theory methods. Validation of the present calculation method is made through comparison with the experiment conducted with a bulk-carrier model advancing in regular oblique waves and motion-free condition. Good agreement between computed and measured results and also superiority of EUT to NSM are confirmed for all modes of ship motion and the steady forces and yaw moment in a wide range of wave frequency.

1 Introduction

It is well known that the resistance of a ship will increase when the ship is advancing in waves at constant forward speed. This increment is called the added resistance, which is the longitudinal component of the wave-induced steady force of second order in the wave amplitude. Since the prediction of ship resistance is crucial for the economic operation in actual seas, many studies on the added resistance have been conducted so far.

In actual seaways, owing to the nature of the ocean, ships must sail obliquely to the direction of wave propagation. In oblique waves, not only the added resistance, but also the same kind of steady sway force and yaw moment may be exerted. As an effect of these steady sway force and yaw moment, the check helm and drift angle of the ship may be exerted to attain equilibrium, which will induce another kind of resistance increase. Therefore, accurate prediction of wave-induced steady force and moment becomes important in considering the maneuvering motion of a ship in waves.

Early development of the theoretical formulation for the added resistance was provided by Maruo [1] by means of the principles of momentum and energy conservation. In the calculation formula derived, the Kochin function, equivalent to the amplitude of ship-generated disturbance waves far from the ship, is needed as the input. Newman [2] studied the wave-induced steady yaw moment on a floating body at zero speed, and derived a formula using the angular momentum conservation principle. Their analyses were based on the stationary-phase method, which is expedient for the zero-speed problem, but becomes messy for the case of forward speed present. In fact, Lin and Reed [3] succeeded in obtaining a formula for the steady sway force using the stationary-phase method, but they found it difficult to derive a formula for the steady yaw moment when the forward speed exists.

Kashiwagi [4,5,6] proposed an analysis method utilizing the Fourier-transform theory to tackle the difficulty of stationary-phase method, and consequently derived the formulae for the steady forces and yaw moment at forward speed. Kashiwagi [5] computed further the Kochin function and then the added resistance, steady sway force, and steady yaw moment for the forward-speed but motion-fixed cases by means of the unified theory of Sclavounos [7]. Later Kashiwagi [8] proposed Enhanced Unified Theory (EUT) as an extension from the unified theory of Newman [9] and Sclavounos [7], and analyzed surge-related problems by retaining the x-component of the normal vector in the body boundary condition and also lateral motion modes in the same fashion as that for heave and pitch, with 3D and forward-speed effects taken into account.

Compared to a large amount of work on the added resistance, few studies have been made on the steady sway force and yaw moment. Naito et al. [10] measured the wave-induced steady forces on a tanker model for motion-fixed cases. Iwashita et al. [11] compared computed results by the 3D Green function method with measured results for the steady sway force and yaw moment only for the diffraction problem, but agreement was not good in shorter waves when the forward speed is present. Another measurement of wave-induced steady forces was conducted by Ueno et al. [12] using a VLCC model at Froude number $Fn=0.069$ in a very short wave. Utilizing a time-domain 3D higher-order boundary element method, Joncquez [13] evaluated the second-order forces and moments for all motion modes at zero speed, but the ship was free to heave and pitch. When the forward speed is considered, evaluation of forces and moment was done only for head-wave case.

For the ship maneuvering problem in waves, Skejic and Faltinsen [14] investigated the time-averaged second-order wave loads utilizing several theories, and compared their computed results for the sway force and yaw moment with available measured data for oblique incident waves. Later Seo and Kim [15] incorporated computed results of wave-induced horizontal forces (added resistance and sway force) and yaw moment into the equations of maneuvering motion of a ship. In beam-sea case, the agreement between simulated and observed results was found to be relatively poor due to considerable drift effects on the turning direction. The discrepancy in the prediction of steady yaw moment was understood to be a significant cause of the difference. Recently Zhang et al. [16] stressed the importance of the wave-induced second-order quantities in the maneuvering motion through the time-domain Rankine panel method, where the trailing vortex sheet is introduced to the double-body flow.

In this paper, study is made on the wave-induced added resistance, steady sway force, and steady yaw moment using the calculation formulae derived by Kashiwagi [4] for the general forward-speed case. The Kochin functions for symmetric and antisymmetric components of ship-disturbance waves are important input in those calculation formulae, and they are computed by EUT and NSM. Special attention is paid on the precise integration method to remove square-root singularities at the limits of integration range and to ensure the convergence in semi-infinite integrals appearing in the calculation formulae not only for the added resistance, but also for the steady sway force and yaw moment. Therefore, the calculation method in this paper is markedly different from conventional ones based on the strip-theory methods in that the numerical integration in the formulae is exactly implemented without introducing any artificial convergence factor and that the computation method for the Kochin function is exact in the framework of the linear slender-ship theory and applicable to all frequencies. In the effort to validate this computation scheme, numerical computations are made for comparison with the experiment conducted by Yasukawa et al. [17] using a bulk carrier model advancing in regular oblique waves with forward speed and six-degree-of-freedom motions.

Fig. 1

Coordinate system and notations

2 Linearized theory of a ship in waves

2.1 Formulation of boundary-value problem

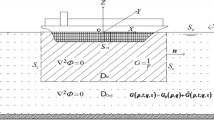
For applying the principles of momentum and energy conservation, we need an expression of the body-disturbance velocity potential valid at a distance from a ship, which advances at constant forward speed U and oscillates with circular frequency $\omega$ in regular waves. For subsequent analyses, a Cartesian coordinate system O-xyz is taken, with the origin placed at the center of a ship and on the undisturbed free surface. As shown in Fig. 1, the x-axis is directed to the ship’s bow and the z-axis is positive downward. The depth of water is assumed infinite. A plane progressive incident wave incoming with angle $\chi$ relative to the x-axis is considered, which has amplitude $\zeta _\mathrm{a}$ and circular frequency $\omega _0$. In this case, the oscillation of a ship occurs with the circular frequency of encounter given by $\omega = \omega _0 -k_0 U \cos \chi$, where $k_0$ is the wave number of incident wave and equal to $\omega _0^2 /g$, with g the acceleration due to gravity.

Under the assumption that the fluid is inviscid with irrotational motion and that the amplitudes of incident wave and ship’s oscillation are small, the velocity potential can be introduced and written as

$$\begin{aligned} {\varPhi }(x, y, z, t) = U\big [ -x +\phi _\mathrm{s} (x, y, z)\big ] +\mathfrak {R}\big [ \phi (x, y, z)\,\mathrm{e}^{i\omega t}\big ], \end{aligned}$$

(1)

where $\phi _\mathrm{s}$ represents the steady disturbance potential due to forward motion of a ship, which will be ignored eventually in this paper with assumption of slenderness of a ship. The spatial part of the unsteady velocity potential $\phi (x, y, z)$ is given as a sum of the incident-wave potential $\phi _0$ and the body-disturbance velocity potential $\phi _\mathrm{B}$. The latter component consists of the scattering and radiation potentials. These are expressed in the form

$$\begin{aligned}&\phi (x, y, z) =\displaystyle \frac{g\zeta _\mathrm{a}}{i\omega _0} \Big \{ \phi _0 (x, y, z) + \phi _\mathrm{B} (x, y, z)\Big \}, \end{aligned}$$

(2)

$$\begin{aligned}&\phi _0 (x, y, z) = \exp \big \{ -k_0 z -i k_0 ( x\cos \chi + y\sin \chi )\big \}, \end{aligned}$$

(3)

$$\begin{aligned}&\phi _\mathrm{B} (x, y, z) = \phi _7 (x, y, z) - \displaystyle \frac{\omega \omega _0}{g} \sum _{j=1}^6 \frac{X_j}{\zeta _\mathrm{a}} \phi _j (x, y, z) . \end{aligned}$$

(4)

The first term $\phi _7$ in Eq. 4 is the scattering potential and the last term $\phi _j$ is the radiation potential due to ship oscillation in six degrees of freedom ($j= 1-6$) with complex amplitude $X_j$ in the j-th mode of motion. Symbol $\mathfrak {R}$ in Eq. 1 means the real part to be taken (likewise, $\mathfrak {I}$ will be used later to mean the imaginary part).

All of the velocity potentials are governed by Laplace’s equation and subject to the free-surface boundary condition given by

$$\begin{aligned}{}[F] \quad \left( i\omega -U\displaystyle \frac{\partial }{\partial x} \right) ^2 \phi -g \displaystyle \frac{\partial \phi }{\partial z} = 0 \quad \text{ on }\ z=0 \end{aligned}$$

(5)

and the condition of vanishing velocity as $z\rightarrow \infty$. In addition, the disturbance potential $\phi _\mathrm{B}$ must satisfy the radiation condition in the far field, and each velocity potential in $\phi _\mathrm{B}$ can be characterized by the body boundary condition

$$\begin{aligned} \displaystyle \frac{\partial \phi _j}{\partial n}\,=\,\, & {} n_j +\displaystyle \frac{U}{i\omega } m_j \quad (j=1-6) \end{aligned}$$

(6)

$$\begin{aligned} \quad\ = & {} - \displaystyle \frac{\partial \phi _0}{\partial n} \quad (j=7), \end{aligned}$$

(7)

where

$$\begin{aligned} \left. \begin{array}{l} (n_1, n_2, n_3) =\varvec{n}, \ (n_4, n_5, n_6) =\varvec{r}\times \varvec{n} \\ (m_1, m_2, m_3) = -\left( \varvec{n}\cdot \nabla \right) \varvec{V} \\ (m_4, m_5, m_6) = -\left( \varvec{n}\cdot \nabla \right) \left( \varvec{r}\times \varvec{V}\right) \\ \varvec{r} =(x, y, z), \ \varvec{V} =\nabla \big [ -x +\phi _s (x, y, z)\big ] \end{array} \right\} . \end{aligned}$$

(8)

Here $n_j$ denotes the jth component of the unit normal vector directing into the fluid and $m_j$ is the so-called m-term representing interactions between the unsteady and steady flows. In the case of uniform-flow approximation for the steady flow field, it follows from Eq. 8 that $m_j=0$ for $j=1-4$, $m_5 = -n_3$, and $m_6 = n_2$.

2.2 Far-field expression of the velocity potential

With Green’s theorem, the body-disturbance potential can be given by

$$\begin{aligned} \phi _\mathrm{B} \left( P \right) =\iint _{S_\mathrm{H}} \left( \displaystyle \frac{\partial \phi _\mathrm{B}}{\partial n} -\phi _\mathrm{B} \frac{\partial }{\partial n} \right) G_{3D} (P; Q)\, \mathrm{d}S(Q), \end{aligned}$$

(9)

where $P =(x, y, z)$ is the field point and $Q=(\xi , \eta , \zeta )$ is the integration point on the wetted ship hull surface $S_\mathrm{H}$; $\partial /\partial n$ is the normal differentiation with respect to Q; $G_{3D} (P; Q)$ denotes the Green function satisfying all homogeneous boundary conditions except for the body boundary condition.

At a large distance far from the ship, the local-wave components decay and thus, we may consider only the progressive wave terms in the Green function, which can be expressed as

$$\begin{aligned} G_{3D} (P; Q) \sim \,&\displaystyle \frac{i}{2\pi } \bigg [ -\int _{-\infty }^{k_1} + \int _{k_2}^{k_3} +\int _{k_4}^\infty \bigg ] \frac{\kappa }{\sqrt{\kappa ^2 - k^2}} \nonumber \\&\times \,\mathrm{e}^{-\kappa (z+\zeta ) -i\epsilon _k |y-\eta |\sqrt{\kappa ^2 -k^2} -ik(x-\xi )}\, \mathrm{d}k , \end{aligned}$$

(10)

$$\begin{aligned}&\left. \begin{array}{l} \kappa =\displaystyle \frac{1}{g} \left( \omega +kU \right) ^2 = K + 2k \tau +\frac{k^2}{K_0} \\ K=\displaystyle \frac{\omega ^2}{g}, \,\ \tau = \frac{U\omega }{g}, \,\ K_0 =\frac{g}{U^2} \\ \epsilon _k =\mathrm{sgn}\left( \omega + kU\right) \end{array}\right\} , \end{aligned}$$

(11)

$$\begin{aligned}&\left. \begin{array}{l} k_1 \\ k_2 \end{array} \right\} = -\displaystyle \frac{K_0}{2} \big ( 1+ 2\tau \pm \sqrt{1+ 4\tau } \big ), \end{aligned}$$

(12)

$$\begin{aligned}&\left. \begin{array}{l} k_3 \\ k_4 \end{array} \right\} = +\displaystyle \frac{K_0}{2} \big ( 1- 2\tau \mp \sqrt{1 - 4\tau } \big ). \end{aligned}$$

(13)

Note that $k_j\ (j=1-4)$ are the limits of integration range, given from $\kappa ^2 =k^2$, and the integration range corresponds to the values satisfying $\kappa ^2 \ge k^2$. In the case of $\tau>1/4$, $k_3$ and $k_4$ become complex and thus the limits of integration should be interpreted as continuous for $k_2 < k$. We also note that $\epsilon _k =-1$ for $k < k_1$ and $\epsilon _k = 1$ for $k_2 < k$. Therefore, the integration range with respect to k may be written in terms of the unit step function $u(\kappa ^2 -k^2)$ as follows:

$$\begin{aligned} \bigg [ -\int _{-\infty }^{k_1} + \int _{k_2}^{k_3} +\int _{k_4}^\infty \bigg ] \ \longrightarrow \ \displaystyle \int _{-\infty }^\infty \epsilon _k\, u(\kappa ^2 -k^2). \end{aligned}$$

Substituting Eq. 10 into Eq. 9, the far-field expression of the disturbance potential can be obtained in the form

$$\begin{aligned} \phi _\mathrm{B} (P) \sim \,&\displaystyle \frac{i}{2\pi } \displaystyle \int _{-\infty }^\infty \epsilon _k\,u(\kappa ^2 -k^2)\,H^\pm (k) \nonumber \\&\times \displaystyle \frac{\kappa }{\sqrt{\kappa ^2 -k^2}} \,\mathrm{e}^{-\kappa z \mp i\epsilon _k y \sqrt{\kappa ^2 -k^2} -ikx}\, \mathrm{d}k , \end{aligned}$$

(14)

where the upper or lower of the complex signs is to be taken according as the sign of y is positive or negative, respectively. $H^\pm (k)$ is the Kochin function equivalent to the complex amplitude of the far-field disturbance wave and expressed as

$$\begin{aligned} H^\pm (k) = C(k) \pm i\epsilon _k\, S(k), \end{aligned}$$

(15)

where

$$\begin{aligned} \left. \begin{array}{l} C(k) \\ S(k) \end{array} \right\} = \iint _{S_\mathrm{H}}&\left( \displaystyle \frac{\partial \phi _\mathrm{B} (Q)}{\partial n} -\phi _\mathrm{B} (Q) \frac{\partial }{\partial n} \right) \,\mathrm{e}^{-\kappa \zeta + ik\xi } \nonumber \\&\times \left\{ \begin{array}{c} \cos \big ( \eta \sqrt{\kappa ^2 -k^2} \big ) \\ \sin \big ( \eta \sqrt{\kappa ^2 -k^2} \big ) \end{array} \right\} \, \mathrm{d}S (\mathrm{Q}) . \end{aligned}$$

(16)

C(k) and S(k) stand for the symmetric and antisymmetric wave components, respectively, with respect to the center plane of a symmetric ship about $y=0$.

Since the disturbance potential is given in a linear superposition as in Eq. 4, the Kochin functions can be written in the same way as follows:

$$\begin{aligned} C(k)\,=\,\, & {} C_7 (k) - \displaystyle \frac{\omega \omega _0}{g} \sum _{j=1,3,5}\frac{X_j}{\zeta _\mathrm{a}}\, C_j (k) , \end{aligned}$$

(17)

$$\begin{aligned} S(k)\,=\,\, & {} S_7 (k) - \displaystyle \frac{\omega \omega _0}{g} \sum _{j=2,4,6}\frac{X_j}{\zeta _\mathrm{a}}\, S_j (k) , \end{aligned}$$

(18)

where $j=1, 3, 5$ denote the longitudinal ship motions (surge, heave and pitch) and $j=2, 4, 6$ the lateral ship motions (sway, roll, and yaw). $X_j /\zeta _\mathrm{a}$ denotes the normalized complex amplitude of jth mode of ship motion, which must be given by solving the ship-motion equations.

3 Calculation formulae for wave-induced steady forces and yaw moment

It is well known that the calculation formulae for wave-induced steady force and moment can be obtained from the principles of momentum and energy conservation, and associated analyses can be done on the control surface far from the ship using the far-field expression of the velocity potential, shown in the previous section.

Maruo [1] derived the formula for the added resistance ($\,\overline{R}\,$) but the analysis using the stationary-phase method was complicated. Kashiwagi [4] showed a simpler analysis by use of Parseval’s theorem in the Fourier transform, and by extending the analysis, he also derived the formulae for the steady sway force ($\,\overline{Y}\,$) and yaw moment ($\,\overline{N}\,$). Those formulae can be summarized as follows:

$$\begin{aligned} \displaystyle \frac{\overline{R}}{\rho g \zeta _\mathrm{a}^2}= & {} \, \displaystyle \frac{1}{4\pi k_0} \int _{-\infty }^\infty \epsilon _k u(\kappa ^2 -k^2) \left\{ \big | C(k)\big |^2 +\big | S(k) \big |^2 \right\} \nonumber \\&\times \displaystyle \frac{\kappa \, (k-k_0 \cos \chi )}{\sqrt{\kappa ^2 -k^2}}\, \mathrm{d}k , \end{aligned}$$

(19)

$$\begin{aligned} \displaystyle \frac{\overline{Y}}{\rho g \zeta _\mathrm{a}^2}= & {} - \displaystyle \frac{1}{4\pi k_0} \int _{-\infty }^\infty \epsilon _k u(\kappa ^2 -k^2) \bigg [ \,\mathfrak {I}\Bigl \{ 2C(k)\,S^*(k) \Bigr \} \nonumber \\- \,\,& {} \left\{ \big | C(k)\big |^2 +\big | S(k) \big |^2 \right\} \displaystyle \frac{k_0 \sin \chi }{\sqrt{\kappa ^2 -k^2}}\,\bigg ] \kappa \, \mathrm{d}k , \end{aligned}$$

(20)

$$\begin{aligned} \displaystyle \frac{\overline{N}}{\rho g \zeta _\mathrm{a}^2}= & {} \, \displaystyle \frac{1}{4\pi k_0} \int _{-\infty }^\infty \epsilon _k u(\kappa ^2 -k^2) \nonumber \\&\times \,\mathfrak {R}\Bigl \{ C^{{\prime }}(k)\,S^*(k) -S^{{\prime }}(k) \,C^*(k)\Bigr \}\kappa \, \mathrm{d}k \nonumber \\&- \displaystyle \frac{\sin \chi }{2}\,\mathfrak {R}\bigg [ H^{{\prime }} (k_0, \chi ) \nonumber \\&\quad +\displaystyle \frac{1}{k_0} \left( \tau + \frac{k_0\cos \chi }{K_0} \right) H(k_0, \chi )\bigg ]. \end{aligned}$$

(21)

Here $C^{{\prime }}(k)$ and $S^{{\prime }}(k)$ in Eq. 21 denote differentiation with respect to k and the asterisk in the superscript stands for the complex conjugate. $H(k_0, \chi )$ are the values of the Kochin function evaluated at $k=k_0 \cos \chi$ and $\pm \epsilon _k \sqrt{\kappa ^2 -k^2} =k_0\sin \chi$. Thus, from Eqs. 15 and 16, we can write as

$$\begin{aligned} H (k_0, \chi )\,=\,\, & {} \iint _{S_\mathrm{H}} \left( \displaystyle \frac{\partial \phi _\mathrm{B} (Q)}{\partial n} - \phi _\mathrm{B}(Q) \frac{\partial }{\partial n} \right) \nonumber \\&\quad \times \,\mathrm{e}^{-k_0 \zeta + ik_0 (\xi \cos \chi + \eta \sin \chi )}\, \mathrm{d}S(Q) \nonumber \\\,=\,\, & {} C(k_0, \chi ) +i\, S(k_0, \chi ) . \end{aligned}$$

(22)

We must realize from these formulae that the Kochin function is an important input and the numerical integration with respect to k must be performed accurately.

4 Overview of enhanced unified theory

In the present study, the EUT is used to provide the body-disturbance velocity potential valid at a distance from the ship and consequently an expression of the Kochin function. The EUT and its results have been explained by Kashiwagi [8, 19] and thus only the overview and some key equations will be given in this section.

The EUT for the radiation problem is basically the same as the unified theory developed by Newman [9]. However, the surge mode ($j=1$) is analyzed in the same fashion as that for heave and pitch and its motion is computed from the coupled motion equations among surge, heave, and pitch. Furthermore, unlike the original unified theory, similar analyses are also made for lateral-motion modes ($j=2, 4, 6),$ which can be found in Kashiwagi [20] and Appendix-1 of Kashiwagi [21].

The diffraction problem in EUT is basically the same as the unified theory described in Sclavounos [7], but the effects of wave diffraction near the bow are taken into account by retaining the x-component ($n_1$) of normal vector in the body boundary condition for the inner problem. These bow diffraction effects are incorporated together with 3D and forward-speed effects in the outer solution through matching between the inner and outer solutions. In fact, the effect of $n_1$ term in the body boundary condition is crucial near the ship ends, giving an important contribution to the surge exciting force and the added resistance. Analyses for the antisymmetric component of the scattering potential are also made, as shown in Appendix-1 of Kashiwagi [21].

In the slender-ship theory, the outer solution valid far from the ship can be expressed with line distributions of 3D sources for the symmetric flow and of 3D doublets for the antisymmetric flow along the x-axis. Thus the disturbance velocity potential may be written in the form

$$\begin{aligned} \phi _j^{(o)} (x, y, z) =&\, \displaystyle \int _L Q_j (\xi )\, G_{3D}^C (x-\xi , y, z)\, \mathrm{d}\xi \nonumber \\&+\displaystyle \int _L D_j (\xi )\, G_{3D}^S (x-\xi , y, z)\, \mathrm{d}\xi . \end{aligned}$$

(23)

Here $G_{3D}^C$ is the 3D Green function considered in Eq. 9 with $\eta =\zeta =0$, physically equivalent to the velocity potential due to the source with unit strength. $Q_j$ denotes its strength, which is unknown but can be determined through matching with the inner solution. Likewise, $G_{3D}^S$ is the velocity potential due to the doublet with unit strength and axis parallel to the y-axis, which is given by

$$\begin{aligned} G_{3D}^S (x, y, z) \equiv -\displaystyle \frac{\partial }{\kappa \partial y} G_{3D} (x, y, z) . \end{aligned}$$

(24)

$D_j$ in Eq. 23 is the unknown strength of the doublet and can be determined through the matching procedure. The range of integration in Eq. 23 is assumed to be from the stern end to the bow end of a ship along the x-axis.

By substituting the asymptotic expression of the Green function Eq. 10 into Eq. 23, we can obtain the expressions for the symmetric and antisymmetric Kochin functions in the following form:

$$\begin{aligned}&C_j (k) =\displaystyle \int _L Q_j (\xi ) \,\mathrm{e}^{ik\xi }\, \mathrm{d}\xi , \end{aligned}$$

(25)

$$\begin{aligned}&S_j (k) = \displaystyle \frac{\sqrt{\kappa ^2-k^2}}{\kappa } \displaystyle \int _L D_j (\xi )\,\mathrm{e}^{ik\xi }\, \mathrm{d}\xi \equiv \displaystyle \frac{\sqrt{\kappa ^2-k^2}}{\kappa }\, \widehat{S}_j (k) . \end{aligned}$$

(26)

In EUT, as a result of matching between the inner and outer solutions, $Q_j$ and $D_j$ are determined by solving the integral equations, whose kernel functions include 3D and forward-speed effects. For instance, for the radiation problem ($j=1-6$), the integral equations are given in the form

$$\begin{aligned} Q_j (x)\,\,+\,\, & {} \displaystyle \frac{i}{2\pi } \Big ( 1-\sigma _3 / \sigma _3^* \Big ) \int _L Q_j (\xi )\, f(x-\xi )\, \mathrm{d}\xi \nonumber \\\,=\,\, & {} \sigma _j (x) +\displaystyle \frac{U}{i\omega }\,\widehat{\sigma }_j (x) \quad \text{ for }\ j=1, 3, 5 , \end{aligned}$$

(27)

$$\begin{aligned} D_j (x)\,\,+\,\, & {} \displaystyle \frac{i}{2\pi } \Big ( 1-\sigma _2 / \sigma _2^* \Big ) \int _L D_j (\xi )\, h(x-\xi )\, \mathrm{d}\xi \nonumber \\\,\,=\,\, & {} \sigma _j (x) +\displaystyle \frac{U}{i\omega }\,\widehat{\sigma }_j (x) \quad \text{ for }\ j=2, 4, 6 . \end{aligned}$$

(28)

Here $\sigma _j (x)$ and $\widehat{\sigma }_j (x)$ on the right-hand side of Eqs. 27 and 28 are 2D Kochin functions which can be computed with the particular solutions in the inner problem considered in the transverse y-z plane at station x.

The solution in the inner problem is sought to satisfy the 2D Laplace equation, the free-surface boundary condition of Eq. 5 with $U=0$, and the body boundary condition of Eqs. 6 and 7 on the contour of transverse section at station x, which will be denoted as $\mathscr {B} (x)$. Its solution for the radiation problem can be written in the form

$$\begin{aligned} \phi _j^{(i)} (x; y, z) = \varphi _j (y, z) + \displaystyle \frac{U}{i\omega } \widehat{\varphi }_j (y, z) + C_j^H (x)\,\varphi ^H (y, z) , \end{aligned}$$

(29)

where $\varphi _j$ and $\widehat{\varphi }_j$ are the particular solutions satisfying the following body boundary conditions:

$$\begin{aligned} \displaystyle \frac{\partial \varphi _j}{\partial n} = n_j,\quad \displaystyle \frac{\partial \widehat{\varphi }_j}{\partial n} = m_j . \end{aligned}$$

(30)

Namely the particular solution in Eq. 29 is exactly the same as the solution in the strip theories. The last term in Eq. 29 stands for a homogeneous solution, which can be given by $\varphi ^H =\varphi _j - \varphi _j^*$ ($j=3$ for symmetric problems and $j=2$ for antisymmetric problems), and its coefficient $C_j^H (x)$ can be determined by the matching with outer solution.

In terms of $\varphi _j$, the Kochin function $\sigma _j$ is computed from

$$\begin{aligned} \sigma _j (x) = \displaystyle \int _{\mathscr {B} (x)} \left( \displaystyle \frac{\partial \varphi _j}{\partial n} -\varphi _j \frac{\partial }{\partial n} \right) \,\mathrm{e}^{-Kz} \left\{ \begin{array}{c} \cos Ky \\ \sin Ky \end{array} \right\} \, d\ell (y, z) , \end{aligned}$$

(31)

where the upper term ($\cos Ky$) in braces should be taken for $j=1, 3, 5$ and the lower term for $j=2, 4, 6$. Likewise $\widehat{\sigma }_j (x)$ is computed in terms of $\widehat{\varphi }_j$ in place of $\varphi _j$ in Eq. 31.

The kernel functions $f(x-\xi )$ and $h(x-\xi )$ in the integral equations of Eqs. 27 and 28 represent the 3D and forward-speed effects. Their explicit expressions are given in Newman and Sclavounos [22] for $f(x-\xi )$ and in Kashiwagi [20] for $h(x-\xi )$. We can see from Eqs. 27 and 28 that if the 3D and forward-speed effects become small, the strengths of source $Q_j$ and doublet $D_j$ may approach the 2D values on the right-side side; which is the case for higher frequencies.

Corresponding expressions for the diffraction problem are provided in Kashiwagi [21]. Expressions for the symmetric and antisymmetric Kochin functions are formally the same as those in Eqs. 25 and 26, respectively, although the integral equations corresponding to Eqs. 27 and 28 are different in form. However, the numerical solutions method for the integral equations can be the same.

5 Numerical integration methods

Once the Kochin function has been obtained as a function of k, the accuracy in computed values of the wave-induced steady forces ($\,\overline{R}$ and $\overline{Y}\,$) and yaw moment ($\,\overline{N}\,$) depends on the numerical integration with respect to k. To be considered for correct numerical integration are the following two issues: (1) removal of square-root singularity at the limit of integration range $k_j\ (j=1-4)$, and (2) precise treatment of semi-infinite integrals to ensure the convergence.

5.1 Removal of singularity at integration limits

We will have to consider two types of integral:

$$\begin{aligned} \mathscr {J}_{23} \equiv \displaystyle \int _{k_2}^{k_3} \frac{F(k)}{\sqrt{\kappa ^2 -k^2}}\, \mathrm{d}k, \ \mathscr {J}_{4} \equiv \displaystyle \int _{k_4}^{\infty } \frac{F(k)}{\sqrt{\kappa ^2 -k^2}}\, \mathrm{d}k . \end{aligned}$$

(32)

The square-root singularity exists in these integrals because of $\sqrt{\kappa ^2 -k^2}=0$ at $k_j\ (j=2, 3, 4)$. To explain the variable transformation method for this issue, let us consider the following two integrals in general:

$$\begin{aligned} \left. \begin{array}{l} \mathscr {A} = \displaystyle \int _a^b \displaystyle \frac{f(x)}{\sqrt{(x-a)(b-x)}}\, \mathrm{d}x \\ \mathscr {B} = \displaystyle \int _b^\infty \frac{f(x)}{\sqrt{(x-a)(x-b)}}\, \mathrm{d}x \end{array} \right\} . \end{aligned}$$

(33)

For integral $\mathscr {A}$, we will use the following transformation of variable:

$$\begin{aligned} x=\displaystyle \frac{b+a}{2} + \frac{b-a}{2}\,\xi , \quad \xi = \sin \theta . \end{aligned}$$

(34)

Then $\mathscr {A}$ can be transformed into the following form:

$$\begin{aligned} \mathscr {A} =\displaystyle \int _{-1}^1 \displaystyle \frac{f(x)}{\sqrt{1-\xi ^2}}\, \mathrm{d}\xi =\int _{-\pi /2}^{\pi /2} f(x)\, \mathrm{d}\theta , \end{aligned}$$

(35)

where x is given by Eq. 34 with $\theta$. We can see no singularity in the last integral with respect to $\theta$, hence the numerical integration can be done in a straightforward manner.

Next, for integral $\mathscr {B}$, similar idea can be applied and the following variable transformation is used

$$\begin{aligned} x=\displaystyle \frac{b+a}{2} +\frac{b-a}{2}\,\xi , \quad \xi =\sqrt{u^2+1} . \end{aligned}$$

(36)

Then we can obtain the result as follows:

$$\begin{aligned} \mathscr {B} =\displaystyle \int _1^\infty \displaystyle \frac{f(x)}{\sqrt{\xi ^2 -1}}\, \mathrm{d}\xi = \int _0^\infty \displaystyle \frac{f(x)}{\sqrt{u^2+1}}\, \mathrm{d}u , \end{aligned}$$

(37)

which contains again no singularity at the integration limit ($u=0$) so that the numerical integration can be performed with conventional schemes. In the present study, the Gauss quadrature has been used to successive integrals with finite integration range.

5.2 Semi-infinite integral

Many studies using the strip theory have been made so far for computing the Kochin function and then the added resistance based on Eq. 19. Most of those studies usually multiply the integrand by an artificial convergence factor, like $\exp (-\kappa z_\mathrm{s})$, to ensure the convergence as $k \rightarrow \infty$, and the value of $z_\mathrm{s}$ is tuned to see reasonably fast convergence and relatively good agreement with experiments. However, this treatment implies that the depth wise position of the line distribution of singularities in the outer solution is not on $z=0$ and hence inconsistent in the context of slender-ship theory. Kashiwagi [5, 6] settled this problem by showing no difficulty in convergence of the integral in Eq. 19 for the added resistance, even if the sources are placed exactly on $z=0$. In this paper, the calculation method in Kashiwagi [5, 6] is extended to the integrals for $\overline{Y}$ and $\overline{N}$, and an analytical mistake in Kashiwagi [5, 6] is corrected.

As an example for explaining the calculation method, let us consider the following semi-infinite integral:

$$\begin{aligned}&\displaystyle \int _{k_4}^\infty \big | C(k) \big |^2 \displaystyle \frac{\kappa \, (k-k_0\cos \chi )}{\sqrt{\kappa ^2 -k^2}}\, \mathrm{d}k \nonumber \\&= \displaystyle \int _{k_4}^\infty \big | C(k) \big |^2 \displaystyle \frac{\big ( 1-\sqrt{1-k^2 /\kappa ^2} \big ) ( k-k_0 \cos \chi )}{\sqrt{\kappa ^2 -k^2}}\, \mathrm{d}k \nonumber \\&\quad + \mathscr {R}_4 - \mathscr {T}_4\,k_0\cos \chi , \end{aligned}$$

(38)

where

$$\begin{aligned} \mathscr {R}_4 \equiv \displaystyle \int _{k_4}^\infty \big | C(k) \big |^2 \,k\, \mathrm{d}k, \ \mathscr {T}_4 \equiv \displaystyle \int _{k_4}^\infty \big | C(k) \big |^2 \, \mathrm{d}k . \end{aligned}$$

(39)

Note that the first term on the right-hand side of Eq. 38 arises no problem in convergence, because $1-\sqrt{1-k^2/\kappa ^2}$ in the numerator becomes rapidly zero as k increases. Therefore, our attention will be focused on how to evaluate the integrals denoted as $\mathscr {R}_4$ and $\mathscr {T}_4$.

At first, with the assumption that k and x are non-dimensionalized with half the ship length L / 2, the Kochin function C(k) is written in the form

$$\begin{aligned} C(k) =\displaystyle \int _{-1}^1 Q(x)\,\mathrm{e}^{ikx}\, \mathrm{d}x . \end{aligned}$$

(40)

After partial integration, it follows that

$$\begin{aligned} C(k) = \displaystyle \frac{i}{k} \int _{-1}^1 Q^{{\prime }} (x) \,\mathrm{e}^{ikx}\, \mathrm{d}x , \end{aligned}$$

(41)

where we have used the assumption of $Q(\pm 1)=0$, that is, both ship ends are closed, which is plausible in the potential-flow problem. Substituting these into Eq. 39, we have

$$\begin{aligned} \left. \begin{array}{l} \mathscr {R}_4 = i\displaystyle \int _{-1}^1 Q^{{\prime }} (x)\, \mathrm{d}x \int _{-1}^1 Q^* (\xi )\ I_4 (\xi -x) \, \mathrm{d}\xi \mathscr {T}_4 = \displaystyle \int _{-1}^1 Q (x) \, \mathrm{d}x \int _{-1}^1 Q^* (\xi )\ I_4 (\xi -x) \, \mathrm{d}\xi \end{array} \right\} , \end{aligned}$$

(42)

where

$$\begin{aligned} I_4 (\xi -x) \equiv \displaystyle \int _{k_4}^\infty \mathrm{e}^{ik(x-\xi )}\, \mathrm{d}k = \pi \delta (\xi -x) -i \displaystyle \frac{\mathrm{e}^{-ik_4 (\xi -x)}}{\xi -x} , \end{aligned}$$

(43)

and $\delta (\xi -x)$ denotes Dirac’s delta function, which is obtained from the following relations:

$$\begin{aligned} \left. \begin{array}{l} \displaystyle \lim _{k\rightarrow \infty } \displaystyle \frac{\cos k (\xi -x)}{\xi -x} = 0 \\ \displaystyle \lim _{k\rightarrow \infty } \displaystyle \frac{\sin k (\xi -x)}{\xi -x} = \pi \,\delta (\xi -x) \end{array} \right\} . \end{aligned}$$

(44)

Substituting Eq. 43 in Eq. 42 gives the following results:

$$\begin{aligned} \mathscr {R}_4= & {} \, i\pi \displaystyle \int _{-1}^1 Q^{{\prime }} (x) Q^* (x)\, \mathrm{d}x \nonumber \\&+ \displaystyle \int _{-1}^1 Q^{{\prime }} (x) \,\mathrm{e}^{ik_4 x}\, \mathrm{d}x \int _{-1}^1 \displaystyle \frac{Q^*(\xi )\,\mathrm{e}^{-ik_4\xi }}{\xi -x}\, \mathrm{d}\xi , \end{aligned}$$

(45)

$$\begin{aligned} \mathscr {T}_4= & {} \, \pi \displaystyle \int _{-1}^1 \big | Q(x) \big |^2\, \mathrm{d}x \nonumber \\&-i \displaystyle \int _{-1}^1 Q (x) \,\mathrm{e}^{ik_4 x}\, \mathrm{d}x \int _{-1}^1 \displaystyle \frac{Q^*(\xi )\,\mathrm{e}^{-ik_4\xi }}{\xi -x}\, \mathrm{d}\xi . \end{aligned}$$

(46)

The first terms on the right-hand side of Eqs. 45 and 46 are missing in the analysis of Kashiwagi [5, 6]. However, we note that these terms have nothing to do with $k_4$, and they will cancel out with corresponding terms to be obtained from the integral for $-\infty< k <k_1$. To show this, let us consider the integral for $-\infty< k < k_1$ in the same way. Namely

$$\begin{aligned}&- \displaystyle \int _{-\infty }^{k_1} \big | C(k) \big |^2 \displaystyle \frac{\kappa \, (k-k_0\cos \chi )}{\sqrt{\kappa ^2 -k^2}}\, \mathrm{d}k \nonumber \\&= \displaystyle \int _{k_1}^{-\infty } \big | C(k) \big |^2 \displaystyle \frac{\big ( 1-\sqrt{1-k^2 /\kappa ^2} \big ) ( k-k_0 \cos \chi )}{\sqrt{\kappa ^2 -k^2}}\, \mathrm{d}k \nonumber \\&\quad + \mathscr {R}_1 - \mathscr {T}_1\,k_0\cos \chi , \end{aligned}$$

(47)

where

$$\begin{aligned} \mathscr {R}_1 \equiv \displaystyle \int _{k_1}^{-\infty } \big | C(k) \big |^2 \,k\, \mathrm{d}k, \ \mathscr {T}_1 \equiv \displaystyle \int _{k_1}^{-\infty } \big | C(k) \big |^2 \, \mathrm{d}k . \end{aligned}$$

(48)

Following the same procedure as that for $\mathscr {R}_4$ and $\mathscr {T}_4$, we come across an integral corresponding to Eq. 43, which can be written by use of Eq. 44 in the form

$$\begin{aligned} I_1 (\xi -x)\equiv & {} \displaystyle \int _{k_1}^{-\infty } \mathrm{e}^{ik(x-\xi )}\, \mathrm{d}k \nonumber \\= & {} - \pi \delta (\xi -x) -i \displaystyle \frac{\mathrm{e}^{-ik_1 (\xi -x)}}{\xi -x} . \end{aligned}$$

(49)

It can be seen that the first term on the right-hand side of Eq. 49 is opposite in sign to that of Eq. 43. Thus, in the end after summing up, there is no contribution from the first terms in Eqs. 45 and 46.

Regarding the singular integral with respect to $\xi$ in Eqs. 45 and 46, the analytical integration method shown in Kashiwagi [5, 6] can be applied, using the Fourier-series representation for the line distribution of sources. The resulting singular integral is the same in form as Glauert’s integral popular in the wing theory and thus can be evaluated analytically. Specifically, introducing the variable transformation of $x=\cos \theta$ and $\xi = \cos \varphi$, we have the following:

$$\begin{aligned} \displaystyle \int _{-1}^1 \displaystyle \frac{Q^* (\xi )\,\mathrm{e}^{-i\nu \xi }}{\xi -x}\, \mathrm{d}\xi= & {} \sum _{n=1}^\infty c_n^* \int _0^\pi \frac{\sin n\varphi \sin \varphi }{\cos \varphi -\cos \theta }\, \mathrm{d}\varphi \nonumber \\= & {} -\pi \displaystyle \sum _{n=1}^\infty c_n^* \cos n\theta , \end{aligned}$$

(50)

where

$$\begin{aligned} \left. \begin{array}{l} Q(x)\,\mathrm{e}^{i\nu x} =\displaystyle \sum _{n=1}^\infty c_n\sin n\theta \\ c_n =\displaystyle \frac{2}{\pi } \int _0^\pi Q(\cos \theta )\,\mathrm{e}^{i\nu \cos \theta } \sin n \theta \, \mathrm{d}\theta \end{array} \right\} \end{aligned}$$

(51)

and $\nu$ must be understood as $k_4$ or $k_1$.

Using these results and performing resultant integrals with respect to $\theta$, $\mathscr {R}_j$ and $\mathscr {T}_j$ ($j=4$ or 1) defined in Eqs. 39 and 48 can be expressed as

$$\begin{aligned} \mathscr {R}_j\,= \,\,& {} (-1)^j \,i\pi \displaystyle \int _{-1}^1 Q^{{\prime }} (x) Q^* (x)\, \mathrm{d}x \nonumber \\&\, +\displaystyle \frac{\pi ^2}{2} \sum _{n=1}^\infty \Bigl [\, k_j \,\mathfrak {I}\big ( c_n\, c_{n+1}^*\big ) + n \left| c_n \right| ^2\Bigr ] , \end{aligned}$$

(52)

$$\begin{aligned} \mathscr {T}_j\,=\,\, & {} (-1)^j \pi \displaystyle \int _{-1}^1 \big | Q(x) \big |^2\, \mathrm{d}x + \frac{\pi ^2}{2} \sum _{n=1}^\infty \mathfrak {I}\big ( c_n \, c_{n+1}^* \big ) . \end{aligned}$$

(53)

As already mentioned, the first terms on the right-hand side of Eqs. 52 and 53 do not contribute to the final result because of cancellation after summing up the terms of $j=1$ and $j=4$. Needless to say, the same calculation method will be used to the integrals related to the antisymmetric component of the Kochin function S(k) in Eq. 19.

The same technique can be applied to the integrals for the steady sway force $\overline{Y}$ in Eq. 20 and for the steady yaw moment $\overline{N}$ in Eq. 21. Let us start with the steady sway force. We will have to consider the following integral:

$$\begin{aligned}&\displaystyle \int _{\nu }^\infty \kappa \,\mathfrak {I}\Bigl \{ C(k) S^* (k) \Bigr \}\, \mathrm{d}k \nonumber \\&= \displaystyle \int _{\nu }^\infty \kappa \Bigl (\sqrt{1-k^2/\kappa ^2} -1\,\Bigr )\, \mathfrak {I}\Bigl \{ C(k) \widehat{S}^* (k)\Bigr \}\, \mathrm{d}k \nonumber \\&\quad + \displaystyle \int _{\nu }^\infty \kappa \, \mathfrak {I}\Bigl \{ C(k) \widehat{S}^* (k)\Bigr \}\, \mathrm{d}k , \end{aligned}$$

(54)

where $\widehat{S} (k)$ is defined in Eq. 26.

It should be noted again that no problem exists in convergence for the first term on the right-hand side of Eq. 54, because $\sqrt{1-k^2 /\kappa ^2}\,\rightarrow \, 1$ rapidly as $k\rightarrow \infty$. Thus we consider the last integral.

Since $\kappa = K + 2k\tau + k^2/K_0$, we should evaluate analytically the following integrals:

$$\begin{aligned} \mathscr {Y}_n \equiv \displaystyle \int _{\nu }^\infty k^n\, \mathfrak {I}\Bigl \{ C(k) \widehat{S}^* (k) \Bigr \}\, \mathrm{d}k, \quad n=0, 1, 2 . \end{aligned}$$

(55)

With these results, the last term in Eq. 54 can be computed from

$$\begin{aligned} \displaystyle \int _{\nu }^\infty \kappa \,\mathfrak {I}\Bigl \{ C(k)\widehat{S}^* (k) \Bigr \}\, \mathrm{d}k = K \,\mathscr {Y}_0 +2\tau \,\mathscr {Y}_1 +\displaystyle \frac{1}{K_0} \mathscr {Y}_2 . \end{aligned}$$

(56)

The analysis for Eq. 55, using the Fourier-series representation for the line distribution of sources and doublets, are rather lengthy and thus, their transformation and results are shown in Appendix of this paper.

Likewise, the semi-infinite integral in the steady yaw moment can be written as follows:

$$\begin{aligned}&\displaystyle \int _{\nu }^\infty \kappa \,\mathfrak {R}\Bigl \{ C^{{\prime }}(k) S^* (k) -S^{{\prime }}(k) C^*(k) \Bigr \}\, \mathrm{d}k \nonumber \\&= \displaystyle \int _{\nu }^\infty \kappa \Bigl ( \sqrt{1- k^2/\kappa ^2} -1\,\Bigr ) \nonumber \\&\quad \times \mathfrak {R}\Bigl \{ C^{{\prime }}(k) \widehat{S}^* (k) -\widehat{S}^{{\prime }}(k) C^*(k) \Bigr \}\, \mathrm{d}k \nonumber \\&\quad + \displaystyle \int _{\nu }^\infty \kappa \,\mathfrak {R}\Bigl \{ C^{{\prime }}(k) \widehat{S}^* (k) -\widehat{S}^{{\prime }}(k) C^*(k) \Bigr \}\, \mathrm{d}k . \end{aligned}$$

(57)

The first term on the right-hand side of Eq. 57 can be numerically integrated without any difficulty. For evaluating the last term in Eq. 57, we consider analytically the following integrals:

$$\begin{aligned} \mathscr {N}_n \equiv \displaystyle \int _{\nu }^\infty k^n\,\mathfrak {R}\Bigl \{ C^{{\prime }} (k) \widehat{S}^* (k) \Bigr \}\, \mathrm{d}k , \quad n=0, 1, 2 , \end{aligned}$$

(58)

$$\begin{aligned} \tilde{\mathscr {N}}_n \equiv \displaystyle \int _{\nu }^\infty k^n\,\mathfrak {R}\Bigl \{ \widehat{S}^{{\prime }} (k) C^* (k) \Bigr \}\, \mathrm{d}k , \quad n=0, 1, 2 . \end{aligned}$$

(59)

With the results of these integrals, we can readily evaluate the last integral in Eq. 57 from

$$\begin{aligned}&\displaystyle \int _{\nu }^\infty \kappa \,\mathfrak {R}\Bigl \{ C^{{\prime }} (k) \widehat{S}^* (k) - \widehat{S}^{{\prime }} (k) C^* (k) \Bigr \}\, \mathrm{d}k \nonumber \\&= K (\mathscr {N}_0 - \tilde{\mathscr {N}}_0 ) +2\tau \, (\mathscr {N}_1 - \tilde{\mathscr {N}}_1 ) +\displaystyle \frac{1}{K_0} (\mathscr {N}_2 - \tilde{\mathscr {N}}_2 ) . \end{aligned}$$

(60)

Table 1 Principal particulars of JASNAOE-BC084 hull

Fig. 2

Length-wise projection of body plan

Fig. 3

Ship-waves encountering angles

The analytical procedure for computing Eqs. 58 and 59 is essentially the same as that for $\mathscr {Y}_n\ (n=0, 1, 2)$, and we note that the calculation of $\tilde{\mathscr {N}}_n$ can be done easily from the result of $\mathscr {N}_n$ simply by exchanging C(k) and $\widehat{S} (k)$. The final expressions for $\mathscr {N}_n$ and $\tilde{\mathscr {N}}_n \ (n=0, 1, 2)$ are summarized in Appendix of this paper.

Fig. 4

Ship motions in bow oblique waves ($\chi =150^\circ$) at 4 knots ($Fn=0.037$)

6 Experiment and tested ship model

Experiments measuring the wave-induced steady forces (added resistance and sway force) and yaw moment have been conducted at the seakeeping and maneuvering model basin of Nagasaki R&D Center, Mitsubishi Heavy Industries, and some of the results are reported by Yasukawa et al. [17]. These experimental data are used for comparison with computations in the present paper.

The ship model used in the experiment is a bulk carrier named JASNAOE-BC084 in full-load condition, which is a modified version from KVLCC2 and its body plan and principal particulars are shown in Yasukawa et al. [18]. Some of the important values in the principal particulars are listed in Table 1, and the length-wise projection of the body is illustrated in Fig. 2.

In this experiment conducted by Yasukawa et al. [17], wave-induced ship motions and steady forces were measured at 4 different forward speeds; they are 0, 4, 8, and 13.5 knots in real-ship scale. For each speed, measurements were carried out at 4 different incident-wave angles ($\chi$) as shown in Fig. 3. In the highest speed case (13.5 knot), the measurement was done only in head waves ($\chi =180^\circ$). The range of wavelengths (the ratio of wavelength to ship length $\lambda /L$) is $\lambda /L =0.4-1.5$, but the wavelength $\lambda /L=0.4$ was not used in oblique waves of $\chi = 30^\circ$ and $90^\circ$.

In all cases, the ship model was set to be free in all modes of ship motion, but coil springs were used to constrain loosely the surge, sway, and yaw motions. According to the report, the incident-wave amplitude was measured by two different wave probes; one is near-field probe installed on the running carriage, upstream of the ship model, and the other is far-field probe fixed spatially near the side wall of the towing tank. At the wavelengths where interaction is intense, for instance where the peaks of forces are measured ($\lambda /L=1.0-1.2$), a large difference was observed in the incident-wave amplitude measured by these two different probes. This phenomenon can be understood, since the record by the near-field probe may include the ship disturbance waves. On the other hand, the record by the far-field probe must contain only negligibly small, or not at all, waves generated by the ship. For this physical reason, the non-dimensional values in terms of the far-field incident-wave amplitudes will be used as the experimental data in this paper.

The amplitude $\zeta _\mathrm{a}$ and maximum slope $k_0 \zeta _\mathrm{a}$ of the incident wave are used for non-dimensional values of the translational and rotational motions, respectively. Time-averaged wave-induced steady forces (added resistance $\overline{R}$ and sway force $\overline{Y}$) and yaw moment $\overline{N}$ are non-dimensionalized with $\rho g \zeta _a^2 (B^2/L)$ and $\rho g \zeta _a^2 LB$, respectively, where $\rho$ is the density of water; g the acceleration of gravity; L the ship length; and B the ship breadth.

7 Results and discussion

Precise prediction of the Kochin functions is of vital importance for computations of the wave-induced steady forces and moment. As shown in Eqs. 17 and 18, the complex amplitude of ship motions, $X_j / \zeta _\mathrm{a}\ (j=1-6)$ must be given for the motion-free case. Therefore, a comparison is made first for the amplitude of ship motions. In oblique waves where antisymmetric motions arises, we observed that the linear computation (considering only the wave-making component for the damping) gives overpredicted roll motion and its coupling, particularly near the resonant peak in roll. Therefore, we introduced an equivalent damping coefficient taking account of viscous effects, based on the component analysis method as formulated by Himeno [23].

Figure 4 shows the non-dimensional amplitudes of wave-induced motions of bulk carrier advancing at 4 knot ($Fn=0.037$) in bow oblique waves ($\chi =150^\circ$). Computed results by EUT and NSM are compared with the experimental data non-dimensionalized by the incident-wave amplitude measured with far-field wave probe (which are denoted as EXP). We can observe remarkable agreement between computed and measured results as well as the superiority of EUT to NSM on certain modes of motion, like heave and roll. Nevertheless, the computed wavelength where the roll motion takes a peak due to its resonance is slightly different from the measured one, which may be attributed to an error in the measurement of roll moment of inertia and vertical position of the center of gravity, although the uncertainty level in the measurement cannot be described explicitly.

As representative examples, the wave-induced added resistance, sway force, and yaw moment at 4 knot ($Fn=0.037$) are presented in Fig. 5 (for $\chi =150^\circ$ and 180$^\circ$) and in Fig. 6 (for $\chi =30^\circ$ and 90$^\circ$). Overall, computed values are in favorable agreement with measured data. EUT is in general better than NSM due to inclusion of 3D and forward-speed effects. In shorter waves, EUT is also prominently superior to NSM, mainly because the effect of $n_1$-term is retained in the body boundary condition for the diffraction problem. It should be noted that the values of $\overline{Y}$ and $\overline{N}$ must be zero in head waves, but as shown in Fig. 5, nonzero values can be observed, which indicates a possible degree of experimental error or noise.

Fig. 5

$\overline{R}$, $\overline{Y}$ and $\overline{N}$ in bow ($\chi =150^\circ$) and head ($\chi =180^\circ$) waves at 4 knot ($Fn=0.037$)

Fig. 6

$\overline{R}$, $\overline{Y}$ and $\overline{N}$ in stern ($\chi =30^\circ$) and beam ($\chi =90^\circ$) waves at 4 knot ($Fn=0.037$)

Fig. 7

Added resistance in head waves at 13.5 knot ($Fn=0.124$)

Fig. 8

Forward-speed effect to steady horizontal forces and moment

At higher forward speed of 13.5 knot ($Fn=0.124$), the measurement was done only for head waves, in which obviously the steady sway force ($\overline{Y}$) and yaw moment ($\overline{N}$) are very small, hence only the added resistance ($\overline{R}$) is depicted in Fig. 7. We note that the peak value of the added resistance tends to be sensitive to the accuracy in the incident-wave amplitude and also to nonlinear effects in ship motion.

As examined previously by Skejic and Faltinsen [14] and Seo and Kim [15], the horizontal steady forces and moment show its large influence on the ship maneuvering trajectory, with emphasis put on the difficulty in computation of steady yaw moment. In maneuvering motions, the amplitude of these second-order quantities in wave amplitude changes at every time step in numerical simulations, depending on varying values of U and $\chi$. Therefore, we checked the steady forces and moment in increasing the forward speed at crucial frequencies in oblique wave condition, and the results of which are shown in Fig. 8.

In relatively short waves ($\lambda /L =0.6$), the superiority of EUT to NSM is evident in the prediction of $\overline{R}$ and $\overline{Y}$. One of the noteworthy points is a significant value of the added resistance even in zero speed due to realistic ship geometry. In contrast, for a fore-aft symmetric ship (e. g., Wigley hull), it is clear that this quantity will be essentially zero.

On the other hand, for the steady yaw moment ($\overline{N}$), we suspect potential difficulty in the computation due to its sensitivity to several parameters. However, relatively good agreement can be confirmed between computed and measured results at $\lambda /L =1.0$.

After all, more validation and improvement of the computation method should be made for higher Froude numbers and other distinct ship geometries.

8 Conclusions

Investigation on the wave-induced steady forces (added resistance and sway force) and yaw moment acting on an advancing ship in oblique waves has been made. We employed enhanced unified theory (EUT) and new strip method (NSM) for solving the radiation and diffraction problems, computing the ship motions in waves and the symmetric and antisymmetric components of the Kochin function equivalent to the complex amplitude of ship-generated disturbance waves at a distance from the ship. These Kochin functions are important input data in the formulae for computing the steady forces and moment based on the principles of momentum and energy conservation. Special attention was paid on the precise computation method ensuring convergence in the semi-infinite integrals appearing in those formulae not only for the added resistance, but also for the steady sway force and yaw moment. The analytical integration method shown in this paper is exact and distinctly different from conventional ones which introduce an artificial convergence factor. For validation of the computation method, we used the experimental data conducted by Yasukawa et al. [17] with a bulk carrier model in the motion-free case with forward speed under several incident-wave angles.

Through a comparison between computed and measured results, we observed that EUT can predict the steady horizontal forces and yaw moment better than NSM. When the wavelength is much small compared to the ship length, the wave diffraction near the ship ends becomes dominant and important for accurate computations of wave-induced steady forces, especially for the added resistance and sway force. The EUT is superior in accounting for the effect of bow wave diffraction, because the x-component of the normal vector is retained in the body boundary condition.

For wavelengths longer than $\lambda /L \approx 1.0$, contribution of the radiation Kochin function becomes important and the radiation Kochin function was found to be rather sensitive to the ship’s forward speed. Therefore, forward-speed effects must be taken into account in a reasonable way for the wave-induced steady horizontal forces and yaw moment.

Appendix Analytical integration for \(\mathscr {Y}_n\), \(\mathscr {N}_n\), and \(\tilde{\mathscr {N}}_n\)

For computing the wave-induced steady sway force and yaw moment, the following integrals are needed to integrate analytically:

$$\begin{aligned}&\mathscr {Y}_n \equiv \displaystyle \int _{\nu }^\infty k^n\,\,\mathfrak {I}\Bigl \{ C(k) \widehat{S}^* (k) \Bigr \}\, \mathrm{d}k, \quad n=0, 1, 2 , \end{aligned}$$

(61)

$$\begin{aligned}&\mathscr {N}_n \equiv \displaystyle \int _{\nu }^\infty k^n \, \mathfrak {R}\Bigl \{ C^{{\prime }} (k) \widehat{S}^* (k) \Bigr \}\, \mathrm{d}k, \quad n=0, 1, 2 , \end{aligned}$$

(62)

$$\begin{aligned}&\tilde{\mathscr {N}}_n \equiv \displaystyle \int _{\nu }^\infty k^n \, \mathfrak {R}\Bigl \{ \widehat{S}^{{\prime }} (k) C^* (k) \Bigr \}\, \mathrm{d}k, \quad n=0, 1, 2 , \end{aligned}$$

(63)

where $\nu$ must be understood as a value equal to or larger than $k_4$ or $|k_1|$.

We consider $\mathscr {Y}_n$ first. By substituting the definition of the Kochin functions C(k) and $\widehat{S} (k)$ shown in Eqs. 25 and 26 and performing partial integration with assumption of $Q(\pm 1)=0$ and $D(\pm 1)=0$, we have

$$\begin{aligned}&\mathscr {Y}_0 = \mathfrak {I}\biggl [\, \displaystyle \int _{-1}^1 Q(x)\, \mathrm{d}x \int _{-1}^1 D^* (\xi )\, \mathrm{d}\xi \int _{\nu }^\infty \mathrm{e}^{ik(x-\xi )}\, \mathrm{d}k\, \biggr ] , \end{aligned}$$

(64)

$$\begin{aligned}&\mathscr {Y}_1 = \mathfrak {I}\biggl [\,i \displaystyle \int _{-1}^1 Q^{{\prime }}(x)\, \mathrm{d}x \int _{-1}^1 D^* (\xi )\, \mathrm{d}\xi \int _{\nu }^\infty \mathrm{e}^{ik(x-\xi )}\, \mathrm{d}k\, \biggr ] , \end{aligned}$$

(65)

$$\begin{aligned}&\mathscr {Y}_2 = \mathfrak {I}\biggl [\, \displaystyle \int _{-1}^1 Q^{{\prime }}(x)\, \mathrm{d}x \int _{-1}^1 D^{*{\prime }} (\xi )\, \mathrm{d}\xi \int _{\nu }^\infty \mathrm{e}^{ik(x-\xi )}\, \mathrm{d}k\, \biggr ] . \end{aligned}$$

(66)

The semi-infinite integral with respect to k can be given by the formula of Eq. 43, but as explained in the analysis for the added resistance, there is no need to consider the contribution from Dirac’s delta function in the final result for the steady sway force as well. To evaluate singular integrals with respect to $\xi$ to be obtained from the last term in Eq. 43, we prepare the following Fourier series:

$$\begin{aligned} \left. \begin{array}{l} D^*(\xi )\,\mathrm{e}^{-i\nu \xi } = \displaystyle \sum _{n=1}^\infty s_n^* \sin n\varphi \\ D^{*{\prime }} (\xi )\,\mathrm{e}^{-i\nu \xi } = -\displaystyle \frac{1}{\sin \varphi } \sum _{n=1}^\infty s_n^* \\ \quad \times \big \{ -i\nu \sin \varphi \sin n\varphi +n\,\cos n\varphi \big \} \\ s_n^* =\displaystyle \frac{2}{\pi } \int _0^\pi D^*(\cos \varphi )\,\mathrm{e}^{-i\nu \cos \varphi } \sin n\varphi \, d\varphi \end{array} \right\} . \end{aligned}$$

(67)

Then the singular integrals with respect to $\xi$ can be analytically integrated like Eq. 50, and the results are written as

$$\begin{aligned}&\displaystyle \int _{-1}^1 \displaystyle \frac{D^* (\xi )\,\mathrm{e}^{-i\nu \xi }}{\xi -x}\, d\xi = - \pi \sum _{n=1}^\infty s_n^* \cos n\theta , \end{aligned}$$

(68)

$$\begin{aligned}&\displaystyle \int _{-1}^1 \displaystyle \frac{D^{*{\prime }} (\xi )\,\mathrm{e}^{-i\nu \xi }}{\xi -x}\, \mathrm{d}\xi = -\pi \sum _{n=1}^\infty s_n^* \nonumber \\&\quad \times \Bigl \{ i\nu \cos n\theta +n\,\displaystyle \frac{\sin n \theta }{\sin \theta }\Bigr \} , \end{aligned}$$

(69)

where $x=\cos \theta$ has been used. Then after substituting Eq. 51, resulting integrals with respect to x can be evaluated as the integrals with respect to $\theta$, for which the following formulae will be used:

$$\begin{aligned}&\displaystyle \int _0^\pi \cos m\theta \sin n\theta \sin \theta \, d\theta =\displaystyle \frac{\pi }{4} \big \{\,\delta _{m+1, n} - \delta _{m, n+1}\,\big \} \end{aligned}$$

(70)

$$\begin{aligned}&\displaystyle \int _0^\pi \cos m \theta \cos n\theta \, d\theta =\!\int _0^\pi \sin m\theta \sin n\theta \, d\theta =\frac{\pi }{2}\,\delta _{m, n} \end{aligned}$$

(71)

$$\begin{aligned}&\displaystyle \int _0^\pi \displaystyle \frac{\sin m\theta \cos n\theta }{\sin \theta }\, d\theta = \left\{ \begin{array}{ll} \pi &{} \ \text{ for }\ m>n \\ 0 &{} \ \text{ otherwise } \end{array} \right. \end{aligned}$$

(72)

where $\delta _{m, n}$ denotes Kroenecker’s delta symbol, equal to 1 when $m=n$ and zero otherwise.

Performing integration using these formulae, we can obtain the following results:

$$\begin{aligned} \mathscr {Y}_0\,=\,\, & {} \mathfrak {I}\bigg [\,-i \displaystyle \int _{-1}^1 Q(x)\,\mathrm{e}^{i\nu x}\, dx \int _{-1}^1 \displaystyle \frac{D^* (\xi )\,\mathrm{e}^{-i\nu \xi }}{\xi -x}\, \mathrm{d}\xi \,\bigg ] \nonumber \\= & {} \displaystyle \frac{\pi ^2}{4} \mathfrak {R}\displaystyle \sum _{n=1}^\infty \bigl \{ \, c_{n+1}\,s_n^* - c_n\, s_{n+1}^*\, \bigr \} , \end{aligned}$$

(73)

$$\begin{aligned} \mathscr {Y}_1\,\,=\,\, & {} \mathfrak {I}\bigg [\, \displaystyle \int _{-1}^1 Q^{{\prime }}(x)\,\mathrm{e}^{i\nu x}\, dx \int _{-1}^1 \displaystyle \frac{D^* (\xi )\,\mathrm{e}^{-i\nu \xi }}{\xi -x}\, d\xi \,\bigg ] \nonumber \\= & {} \displaystyle \frac{\pi ^2}{4} \mathfrak {R}\displaystyle \sum _{n=1}^\infty \Bigl [\, \nu \bigl \{ \, c_{n+1}\,s_n^* - c_n\, s_{n+1}^*\, \bigr \} -i \big ( 2n\,c_n\,s_n^* \big ) \Bigr ] , \end{aligned}$$

(74)

$$\begin{aligned} \mathscr {Y}_2\,\,=\,\, & {} \mathfrak {I}\bigg [\, -i \displaystyle \int _{-1}^1 Q^{{\prime }}(x)\,\mathrm{e}^{i\nu x}\, dx \int _{-1}^1 \displaystyle \frac{D^{*{\prime }} (\xi )\,\mathrm{e}^{-i\nu \xi }}{\xi -x}\, d\xi \,\bigg ] \nonumber \\= & {} \displaystyle \frac{\pi ^2}{4} \mathfrak {R}\displaystyle \sum _{n=1}^\infty \Bigl [\, \nu ^2 \bigl \{ c_{n+1}\,s_n^* - c_n\, s_{n+1}^*\, \bigr \} -i\nu \big ( 4n\,c_n\,s_n^* \big ) \nonumber \\&+ 2n \displaystyle \sum _{\ell =1}^\infty (n+2\ell -1) \bigl \{\, c_{n+2\ell -1}\, s_n^* - s_{n+2\ell -1}\, c_n^* \bigr \}\Bigr ] \quad \end{aligned}$$

(75)

where the Fourier-series coefficient $c_n$ is given in Eq. 51.

Next we consider $\mathscr {N}_n$ and $\tilde{\mathscr {N}}_n$. We note that $\tilde{\mathscr {N}}_n$ can be computed from the results of $\mathscr {N}_n$, simply by replacing $c_n$ and $s_n^*$ with $s_n$ and $c_n^*$, respectively, in the Fourier-series coefficients.

In the calculation for $\mathscr {N}_n$ and $\tilde{\mathscr {N}}_n$, the derivatives of the Kochin functions with respect to k are needed, which can be given simply as

$$\begin{aligned} \left. \begin{array}{l} C^{{\prime }} (k) = \displaystyle \int _{-1}^1 ix\, Q(x)\,\mathrm{e}^{ikx}\, dx \\ \widehat{S}^{{\prime }} (k) = \displaystyle \int _{-1}^1 ix\, D(x) \,\mathrm{e}^{ikx}\, dx \end{array} \right\} . \end{aligned}$$

(76)

Since the analytical procedure is almost the same as that for $\mathscr {Y}_n \ (n=0, 1, 2)$, only the final results for $\mathscr {N}_n \ (n=0, 1, 2)$ are written below.

$$\begin{aligned} \mathscr {N}_0= & {} -\displaystyle \frac{\pi ^2}{8} \mathfrak {R}\displaystyle \sum _{n=1}^\infty \big (\, c_{n+2}\, s_n^* - c_n\,s_{n+2}^* \,\big ) , \end{aligned}$$

(77)

$$\begin{aligned} \mathscr {N}_1= & {} - \displaystyle \frac{\pi ^2}{8} \mathfrak {R}\sum _{n=1}^\infty \Big [ \,\nu \big (\, c_{n+2}\, s_n^* - c_n\,s_{n+2}^* \,\big ) \nonumber \\&\quad - i\, 2 \big \{ n\,c_{n+1}\, s_n^* + (n+1) \,c_n\, s_{n+1}^* \big \} \Big ] ,\end{aligned}$$

(78)

$$\begin{aligned} \mathscr {N}_2= & {} - \displaystyle \frac{\pi ^2}{8} \mathfrak {R}\sum _{n=1}^\infty \bigg [ \, \nu ^2 \big (\, c_{n+2}\, s_n^* - c_n\,s_{n+2}^* \,\big ) \nonumber \\&\quad -i\,\nu 4 \big \{ n\,c_{n+1}\, s_n^* + (n+1)\, c_n\, s_{n+1}^* \big \} \nonumber \\&\quad - 4\, n\, c_n \displaystyle \sum _{\ell =1}^\infty \Big \{ (n+2\ell )\, s_{n+2\ell }^* \nonumber \\&\quad +(n+2\ell -2) \, s_{n+2\ell -2}^* \Big \}\,\bigg ] . \end{aligned}$$

(79)