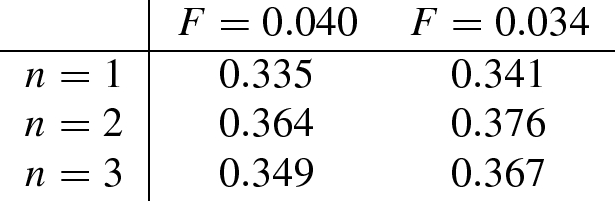Abstract
We examine the strategic use of corporate social responsibility (CSR) in imperfectly competitive markets. Before firms decide upon supply, they choose a level of CSR which determines the weight they put on consumer surplus in their objective function. First, we consider Cournot competition and show that the endogenous level of CSR is positive for any given number of firms. However, positive CSR levels imply smaller equilibrium profits. Second, we find that an incumbent monopolist can use CSR as an entry deterrent. Both results indicate that CSR may increase market concentration. Finally, we show that CSR levels decrease as the degree of product heterogeneity increases in Cournot competition and are zero in Bertrand Competition.
Similar content being viewed by others
Notes
A second important branch relies on the assumption that (some) consumers have a higher willingness to pay for socially responsibly (Baron 2009; García-Gallego and Georgantzís 2009; Manasakis et al. 2013, 2014; Liu et al. 2015; Pecorino 2016) or environmentally friendly (Arora and Gangopadhyay 1995; Cremer and Thisse 1999; Tian 2003; Bansal and Gangopadhyay 2003) produced goods and models CSR as a form of product differentiation.
Lambertini and Tampieri (2012, 2015), Lambertini (2013), and Lambertini et al. (2016) include both consumer surplus and some environmental externality in the objective function of a socially responsible firm. Incorporating consumer surplus in the objective function of a firm is also a widely-used way of taking all kinds of non-profit motives into account (see, e.g., Goering 2007, 2008; Lien 2002; Saha 2014). Models of consumer cooperatives (Mikami 2003; Marini and Zevi 2011; Kopel and Marini 2014) put full weight on consumer surplus and no weight on profits.
In an extension to their baseline model, Fanti and Buccella (2017a, Supplement) also allow for a continuous decision on CSR levels which, however, leads to a different game structure and the possibility of asymmetric equilibria. In Sect. 5.1, we discuss the similarities and differences in more detail.
In fact, constant marginal costs do not influence the equilibrium level of CSR as long as they are symmetric.
This two-stage game may be understood as a model of strategic delegation (Vickers 1985; Fershtman and Judd 1987; Sklivas 1987) offering a commitment to CSR (Baron 2008; Kopel and Brand 2012; Manasakis et al. 2014; Kopel and Lamantia 2016). Alternatively, it may be interpreted as an indirect evolutionary game (Güth and Yaari 1992; Königstein and Müller 2001) in which the most profitable CSR levels prevail.
The following table contains the respective values of total surplus net of aggregate fixed costs in a market without CSR:
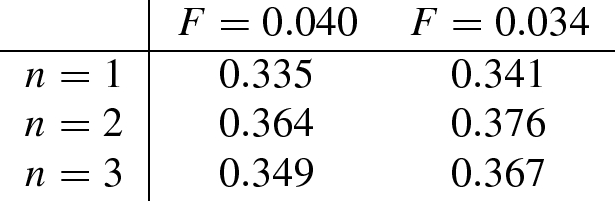
.
This leads to the testable hypothesis that large firms engage more in CSR than small ones.
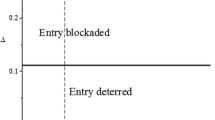
The assumption of Cournot competition in the second stage of entry games is standard in a major part of the literature (see, e.g., Dixit 1980; Maskin 1999; Fanti and Buccella 2017c) and modern textbooks (see, e.g., Belleflamme and Peitz 2015) and allows for a close link to the analysis of Sect. 3. Assuming Stackelberg competition instead will increase (decrease) the range of blockaded/deterred entry if the incumbent is the leader (follower) but does not change the results qualitatively (Dixit 1980).
\(e^* \approx 0.0034\).
This basic tradeoff will remain qualitatively unchanged if we assume Stackelberg competition instead of Cournot competition in the second stage of the entry game, whereas its exact solution obviously depends on the form of competition.
Notice that an increase in the CSR-level always implies an upward-shift of the reaction function (16) because \(\frac{dq_i}{d\theta _i}= \frac{1+\gamma q_j}{(2-\theta _i)^2} >0\) for all \(0< |\gamma | < 1\) and \(i \not = j\).
Notice, however, that this negative result hinges on our assumption that a firm’s demand does not depend directly on its level of CSR. Instead, if consumers have a preference for socially responsibly produced goods CSR may be used strategically as a means of product differentiation and possibly reduce competition this way (Conrad 2005; Liu et al. 2015).
The reason is that a CSR level of zero will never be a best response if it can be freely adjusted but might be a better response (to 0 or k) than k.
See Planer-Friedrich and Sahm (2018) for an explicit formulation of such a game structure in the context of CSR.
Hahn’s condition is known to be a sufficient condition for the strategic success of various kinds of manipulations of a firm’s objective function, while often it imposes a stricter condition than necessary (Cornes and Itaya 2016).
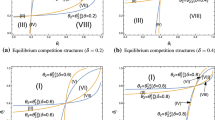
Although the formal analysis (of the first stage of the game) is not tractable for an arbitrary number of firms (\(n>2\)), the corresponding reaction function (in the second stage of the game) is then given by \(q_i = \frac{1-\gamma (1-\theta _i)\sum _{j \not = i}q_j}{2-\theta _i}\) and illustrates that the subgames of the second stage are aggregative in the sense that a firm’s output decision depends only on the sum of all other firms’ outputs. Therefore, firm i’s strategic incentives to commit to a certain reaction function by the choice of an appropriate CSR-level \(\theta _i\) in stage 1 of the game are, qualitatively, the same as in the case with only one opponent (n = 2).
Although the formal analysis (of the first stage of the game) is not tractable for an arbitrary number of firms (\(n>2\)), the corresponding reaction function (in the second stage of the game) is then given by \(p_i = \frac{(1-\theta _i)(1-\gamma +\gamma \sum _{j \not = i}p_j)}{(2-\theta _i)[1+(n-2)\gamma ]}\) and illustrates that the subgames of the second stage are aggregative in the sense that a firm’s price decision depends only on the sum of all other firms’ prices. Therefore, firm i’s strategic incentives to commit to a certain reaction function by the choice of an appropriate CSR-level \(\theta _i\) in stage 1 of the game are, qualitatively, the same as in the case with only one opponent (n = 2).
References
Amir R, De Castro L, Koutsougeras L (2014) Free entry versus socially optimal entry. J Econ Theory 154:112–125
Arora S, Gangopadhyay S (1995) Toward a theoretical model of voluntary overcompliance. J Econ Behav Organ 28(3):289–309
Bansal S, Gangopadhyay S (2003) Tax/subsidy policies in the presence of environmentally aware consumers. J Environ Econ Manag 45:333–355
Baron DP (2001) Private politics, corporate social responsibility, and integrated strategy. J Econ Manag Strategy 10(1):7–45
Baron DP (2008) Managerial contracting and corporate social responsibility. J Public Econ 92(1–2):268–288
Baron DP (2009) A positive theory of moral management, social pressure, and corporate social performance. J Econ Manag Strategy 18(1):7–43
Belleflamme P, Peitz M (2015) Industrial organization, 2nd edn. Cambridge University Press, Cambridge
Bénabou R, Tirole J (2010) Individual and corporate social responsibility. Economica 77(305):1–19
Benn S, Bolton D (2011) Key concepts in corporate social responsibility. SAGE key concepts series. SAGE, London
Boulouta I, Pitelis CN (2014) Who needs CSR? The impact of corporate social responsibility on national competitiveness. J Bus Ethics 119(3):349–364
Brand B, Grothe M (2015) Social responsibility in a bilateral monopoly. J Econ 115(3):275–289
Chen CL, Liu Q, Li J, Wang LF (2016) Corporate social responsibility and downstream price competition with retailer’s effort. Int Rev Econ Finance 46:36–54
Conrad K (2005) Price competition and product differentiation when consumers care for the environment. Environ Resource Econ 31(1):1–19
Cornes R, Itaya J-I (2016) Alternative objectives in an oligopoly model: an aggregative game approach. CESifo working paper no. 6191
Cremer H, Thisse J-F (1999) On the taxation of polluting products in a differentiated industry. Eur Econ Rev 43(3):575–594
Dixit A (1980) The role of investment in entry-deterrence. Econ J 90(357):95–106
Eccles RG, Ioannou I, Serafeim G (2014) The impact of corporate sustainability on organizational processes and performance. Manag Sci 60(11):2835–2857
Fanti L, Buccella D (2017a) Corporate social responsibility in a game-theoretic context. Econ Politica Ind 44(3):371–390
Fanti L, Buccella D (2017b) Corporate social responsibility, profits and welfare with managerial firms. Int Rev Econ 64(4):341–356
Fanti L, Buccella D (2017c) The effects of corporate social responsibility on entry. Econ Politica Ind 44(2):259–266
Fanti L, Buccella D (2018) Profitability of corporate social responsibility in network industries. Int Rev Econ 65(3):271–289
Fernández-Kranz D, Santaló J (2010) When necessity becomes a virtue: the effect of product market competition on corporate social responsibility. J Econ Mang Strategy 19(2):453–487
Fershtman C, Judd KL (1987) Equilibrium incentives in oligopoly. Am Econ Rev 77(5):927–940
Flammer C (2015) Does corporate social responsibility lead to superior financial performance? A regression discontinuity approach. Manag Sci 61(11):2549–2568
García-Gallego A, Georgantzís N (2009) Market effects of changes in consumers’ social responsibility. J Econ Manag Strategy 18(1):235–262
Garriga E, Melé D (2004) Corporate social responsibility theories: mapping the territory. J Bus Ethics 53(1–2):51–71
Goering GE (2007) The strategic use of managerial incentives in a non-profit firm mixed duopoly. Manag Decis Econ 28(2):83–91
Goering GE (2008) Welfare impacts of a non-profit firm in mixed commercial markets. Econ Syst 32(4):326–334
Goering GE (2012) Corporate social responsibility and marketing channel coordination. Res Econ 66(2):142–148
Goering GE (2014) The profit-maximizing case for corporate social responsibility in a bilateral monopoly. Manag Decis Econ 35(7):493–499
Graf C, Wirl F (2014) Corporate social responsibility: a strategic and profitable response to entry? J Bus Econ 84(7):917–927
Güth W, Yaari M (1992) An evolutionary approach to explain reciprocal behavior in a simple strategic game. In: Witt U (ed) Explaining process and change—approaches to evolutionary economics. University of Michigan Press, Ann Arbor, pp 23–34
Häckner J (2000) A note on price and quantity competition in differentiated oligopolies. J Econ Theory 93(2):233–239
Hahn FH (1962) The stability of the Cournot oligopoly solution. Rev Econ Stud 29(4):329–331
Jo H, Harjoto MA (2011) Corporate governance and firm value: the impact of corporate social responsibility. J Bus Ethics 103(3):351–383
Kemper J, Schilke O, Reimann M, Wang X, Brettel M (2013) Competition-motivated corporate social responsibility. J Bus Res 66(10):1954–1963
Kitzmueller M, Shimshack J (2012) Economic perspectives on corporate social responsibility. J Econ Lit 50(1):51–84
Königstein M, Müller W (2001) Why firms should care for customers. Econ Lett 72(1):47–52
Kopel M (2015) Price and quantity contracts in a mixed duopoly with a socially concerned firm. Manag Decis Econ 36(8):559–566
Kopel M, Brand B (2012) Socially responsible firms and endogeneous choice of strategic incentives. Econ Model 29(3):982–989
Kopel M, Lamantia F (2016) Mixed industry outcomes in oligopoly markets with socially concerned firms. University of Graz and University of Calabria, Mimeo
Kopel M, Marini MA (2014) Strategic delegation in consumer cooperatives under mixed oligopoly. J Econ 113(3):275–296
Kopel M, Lamantia F, Szidarovszky F (2014) Evolutionary competition in a mixed market with socially concerned firms. J Econ Dyn Control 48:394–409
KPMG (2015) Currents of change: the KPMG survey of corporate responsibility reporting 2015
Lambertini L (2013) Oligopoly, the environment and natural resources. Routledge, London
Lambertini L, Tampieri A (2012) Corporate social responsibility and firms’ ability to collude. In: Boubaker S, Nguyen DK (eds) Board directors and corporate social responsibility. Palgrave Macmillan, Basingstoke, pp 167–178
Lambertini L, Tampieri A (2015) Incentives, performance and desirability of socially responsible firms in a Cournot oligopoly. Econ Model 50:40–48
Lambertini L, Palestini A, Tampieri A (2016) CSR in an asymmetric duopoly with environmental externality. South Econ J 83(1):236–252
Lien D (2002) Competition between nonprofit and for-profit firms. Int J Bus Econ 1(3):193–207
Liu C-C, Wang LFS, Lee S (2015) Strategic environmental corporate social responsibility in a differentiated duopoly market. Econ Lett 129:108–111
López MV, Garcia A, Rodriguez L (2007) Sustainable development and corporate performance: a study based on the Dow Jones sustainability index. J Bus Ethics 75(3):285–300
Manasakis C, Mitrokostas E, Petrakis E (2013) Certification of corporate social responsibility activities in oligopolistic markets. Can J Econ 46(1):282–309
Manasakis C, Mitrokostas E, Petrakis E (2014) Strategic corporate social responsibility activities and corporate governance in imperfectly competitive markets. Manag Decis Econ 35(7):460–473
Mankiw NG, Whinston MD (1986) Free entry and social inefficiency. Rand J Econ 17(1):48–58
Margolis JD, Walsh JP (2003) Misery loves companies: rethinking social initiatives by business. Adm Sci Q 48(2):268–305
Margolis JD, Elfenbein HA, Walsh JP (2009) Does it pay to be good...and does it matter? A meta-analysis of the relationship between corporate social and financial performance. Working paper. Available at SSRN. https://doi.org/10.2139/ssrn.1866371. Last access 17 Nov 2014
Marini MA, Zevi A (2011) ‘Just one of us’: consumers playing oligopoly in mixed markets. J Econ 104(3):239–263
Maskin ES (1999) Uncertainty and entry deterrence. Econ Theory 14(2):429–437
McWilliams A, Siegel D (2000) Corporate social responsibility and financial performance: correlation or misspecification? Strateg Manag J 21(5):603–609
Mikami K (2003) Market power and the form of enterprise: capitalist firms, worker-owned firms and consumer cooperatives. J Econ Behav Organ 52(4):533–552
Pecorino P (2016) A portion of profits to charity: corporate social responsibility and firm profitability. South Econ J 83(2):380–398
Planer-Friedrich L, Sahm M (2018) Why firms should care for all consumers. Econ Bull 38(3):1603–1612
Saha S (2014) Firm’s objective function and product and process R&D. Econ Model 36:484–494
Sharma A (2018) A note on stackelberg equilibrium in duopoly: strategic use of corporate social responsibility. Econ Bull 38(4):1720–1726
Singh N, Vives X (1984) Price and quantity competition in a differentiated duopoly. RAND J Econ 15(4):546–554
Sklivas SD (1987) The strategic choice of managerial incentives. RAND J Econ 18(3):452–458
Spence AM (1977) Entry, capacity, investment and oligopolistic pricing. Bell J Econ 8(2):534–544
Tian H (2003) Eco-labelling scheme, environmental protection, and protectionism. Can J Econ 36(3):608–633
Tzavara D (2008) Entrant companies competing with “green” incumbents—incentives to refrain from CSR. Working paper
Vickers J (1985) Delegation and the theory of the firm. Econ J 95(Supplement: Conference Papers):138–147
Zhang R, Zhu J, Yue H, Zhu C (2010) Corporate philanthropic giving, advertising intensity, and industry competition level. J Bus Ethics 94(1):39–52
Acknowledgements
We thank two anonymous referees and the participants of the following conferences, workshops, and seminars for their helpful comments and suggestions: Oligo Workshop 2015 (Madrid), 6th Bavarian Micro Day 2015 (Bamberg), Public Economics Research Seminar 2015 (Munich), Annual Meeting of the European Economic Association 2015 (Mannheim), Economic Research Seminar at TUM 2015 (Munich), CESifo Area Conference on Applied Microeconomics 2016 (Munich), Joint Annual Meeting of the Slovak Economic Association and the Austrian Economic Association (NOeG-SEA) 2016 (Bratislava), 22nd BGPE Research Workshop 2016 (Munich), 5th World Congress of the Game Theory Society (GAMES) 2016 (Maastricht), 43rd Annual Conference of the European Association for Research in Industrial Economics (EARIE) 2016 (Lisbon), Economics Research Seminar at UJI 2018 (Castellón de la Plana).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
A Proof of Proposition 3 and Corollary 5
Given the inverse demands (14), consumer surplus can be written as follows:
In the second stage of the game, firm \(i \in \{1,2\}\) chooses \(q_i\) in order to maximize \(V_i=\pi _i + \theta _i CS\). For \(i,j \in \{1,2\}\), \(i \not = j\), the first-order conditions \(\frac{\partial V_i}{\partial q_i} = 0\) imply the reaction functionsFootnote 18
Solving the system of equations (16) yields
for \(i,j \in \{1,2\}\), \(i \not = j\). We now use (14) and (17) to compute the corresponding prices
In the first stage of the game, firm \(i \in \{1,2\}\) chooses \(\theta _i\) in order to maximize \(\pi _i=p_iq_i\). Using (17) and (18), the first-order conditions \(\frac{\partial \pi _i}{\partial \theta _i} = 0\) imply the reaction functions
for \(i,j \in \{1,2\}\), \(i \not = j\). Solving the system of equations (19) for \(i,j \in \{1,2\}\), \(i \not = j\) yields a unique feasible solution:Footnote 19
Using (20), it is straightforward to show that \(\frac{d\theta _C^*(\gamma )}{d\gamma } > 0\) for \(\gamma >0\), and \(\frac{d\theta _C^*(\gamma )}{d\gamma } < 0\) for \(\gamma <0\). This proves Proposition 3.
Finally, to prove Corollary 5, we use (20) and compute firm i’s equilibrium profit
whereas the regular Cournot profit without strategic CSR (\(\theta _1=\theta _2=0\)) equals \(\pi _i^C=\frac{1}{(2+\gamma )^2}\). A comparison shows that, in the relevant range, \(\pi _i^* > \pi _i^C\) if and only if \(-1< \gamma <0\).
B Proof of Proposition 4
The inverse demand functions (14) imply the following direct demands
for \(i,j \in \{1,2\}\), \(i\ne j\). Using (15) and (21), consumer surplus can be expressed in terms of prices:
In the second stage of the game, firm \(i \in \{1,2\}\) chooses \(p_i\) in order to maximize \(V_i=\pi _i + \theta _i CS\). For \(i,j \in \{1,2\}\), \(i \not = j\), the first-order conditions \(\frac{\partial V_i}{\partial p_i} = 0\) imply the reaction functionsFootnote 20
Solving the system of equations (22) yields
for \(i,j \in \{1,2\}\), \(i \not = j\). We now use (21) and (23) to compute the corresponding profits
In the first stage of the game, firm \(i \in \{1,2\}\) chooses \(\theta _i\) in order to maximize \(\pi \). Using (24), it is straightforward to show that for \(i,j \in \{1,2\}\), \(i \not = j\)
for all \(0<|\gamma |<1\). Consequently, each firm \(i \in \{1,2\}\) will choose the lowest CSR level possible, i.e., \(\theta _i=0=:\theta ^*_B(\gamma )\).
C Proof of Proposition 5
At the second stage, the objective functions of the two firms are given by
The maximizing quantities satisfy the first-order conditions
as well as the second order conditions \(\dfrac{\partial ^2 V_i}{\partial q_i^2} < 0\). Using \(CS(q_1+q_2)=\int _0^{q_1+q_2}[p(q)-p(q_1+q_2)]dq\) and thus \(CS'(q_1+q_2)=-(q_1+q_2)p'(q_1+q_2)\), we rewrite Eqs. (26) and (27):
Denote the left-hand side of Eqs. (28) and (29) by \(F_1(\theta _1,\theta _2,q_1,q_2)\) and \(F_2(\theta _1,\theta _2, q_1,q_2)\), respectively.
First, we compute the sign of \(dq_1/d\theta _1\). Treating \(\theta _2\) as fixed and applying the implicit function theorem yields
Notice that \(\partial F_1/\partial \theta _1=-(q_1+q_2)p'(q_1+q_2)>0\). Moreover, \(\partial F_i/\partial q_i=\partial ^2V_i/\partial q_i^2<0\) for \(i \in \{1,2\}\), as implied by the second order conditions on the solution of the maximization problem. Thus the numerator of (30) is positive. Taking the respective derivatives, using the symmetry \(\theta _1=\theta _2=\theta \) in equilibrium, writing \(q_1+q_2=Q\), and simplifying terms, we compute the denominator
Due to \(p'(Q)<0\), an increase in a firm’s CSR level will increase its output, i.e., \(dq_1/d\theta _1>0\), if and only if
Next, we compute the sign of \(d q_1/d \theta _2\). Treating \(\theta _1\) as fixed now and applying the implicit function theorem yields
The denominator of (33) equals that of (30). Again due to the symmetry in equilibrium, the numerator simplifies to
Due to \(-Qp'(Q)>0\), an increase in a firm’s CSR level will decrease its rival’s output, \(dq_1/d\theta _2<0\), if and only if
and
are either both positive or both negative, such that either the numerator of (33) is positive and the denominator of (33) is negative or vice versa. Note that (35) < (36) and thus we obtain the condition that \(dq_1/d\theta _2<0\) if and only if either
or
Finally, notice that (37) and (32) can never both be fulfilled at the same time and that (38) already implies (32).
Rights and permissions
About this article
Cite this article
Planer-Friedrich, L., Sahm, M. Strategic corporate social responsibility, imperfect competition, and market concentration. J Econ 129, 79–101 (2020). https://doi.org/10.1007/s00712-019-00663-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00712-019-00663-x
Keywords
- Corporate social responsibility
- Cournot competition
- Market concentration
- Entry deterrence
- Strategic delegation
- Bertrand competition