Skip to main content
SpringerLink
Log in

Stochastic accumulation of human capital and welfare in the Uzawa–Lucas model: an analytical characterization

  • Published:
Journal of Economics Aims and scope Submit manuscript

Abstract

Stochastic growth models are often solved numerically, because they are not tractable in general. However, recent several studies find the closed-form solution to the stochastic Uzawa–Lucas model in which technological progress or population dynamics follow a Brownian motion process with one or two parameter restriction(s). However, they assume that the return on the accumulation of human capital is deterministic, which is inconsistent with empirical evidence. Therefore, I develop the Uzawa–Lucas model in which the accumulation of human capital follows a mixture of a Brownian motion process and many Poisson jump processes, and obtain the closed-form solution. Moreover, I use it to examine the nexus between human capital uncertainty, technological progress, expected growth rate of human capital, and welfare.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. The other approach is to abstract from the depreciation of capital. See the introduction of Bucci et al. (2011) and Wälde (2011a) for a list of studies that have tried getting the explicit solution to stochastic growth models.

  2. In virtue of a variety of mathematical techniques, Hiraguchi (2009), Naz et al. (2016) and Chaudhry and Naz (2018) also find the closed-form solution to the Uzawa–Lucas model in continuous time, though in the deterministic setup.

  3. An explicit incorporation of leisure makes it extremely difficult to obtain the analytical solution. Therefore, I abstract from it. See Ladrón-De-Guevara et al. (1999) for the deterministic Uzawa–Lucas model with leisure. No study has found the closed-form solution to the stochastic Uzawa–Lucas model with leisure.

  4. We can be sure that \(u\in (0,1)\) as long as the inequality

    $$\begin{aligned} \alpha b-\alpha \delta _h-\frac{\sigma _h^2}{2}\alpha (1-\alpha )+\mu \gamma<\rho <b-\alpha \delta _h-\frac{\sigma _h^2}{2}\alpha (1-\alpha )+\mu \gamma \end{aligned}$$

    holds. Moreover, one can establish that the TVC

    $$\begin{aligned} \lim _{t\rightarrow \infty } E[e^{-\rho t}K^{\alpha +\gamma }] = \lim _{t\rightarrow \infty } E[e^{-\rho t}A^{\gamma }H^\alpha ] = 0 \end{aligned}$$

    is satisfied. The proof requires the verification theorem. See Chang (2004, Ch. 4) for details of this theorem. Hiraguchi (2013, Appendix B) provides an excellent proof of the TVC for the stochastic Uzawa–Lucas model in which technology follows a geometric Brownian motion process. To save space, I will not mention the proof of TVC in what follows.

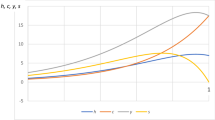
  5. For example, on the one hand, Lucas (2003) claims that \(\phi \) ranges from 1 (log utility) to 4, but on the other, Smith (2007) says that \(\phi \) should be smaller than 1.

  6. See also Eq. (16) in Bucci et al. (2011), Eq. (11) in Marsiglio and Torre (2012a), and Eq. (50) in Marsiglio and Torre (2012b).

  7. Following the seminal paper of Mankiw et al. (1992, p. 432), I set the human capital share \(\alpha =1/3\). For physical capital share, it has been commonplace in macroeconomics to assume that it is also 1/3. However, as Karabarbounis and Neiman (2014) document, the labor share is declining (or, put differently, physical capital share is rising) globally. Therefore, I set \(\gamma =0.27\) so that the physical capital share roughly equals 0.40, the value used by Ahn et al. (2017). \(b=0.11\) is used when Barro and Sala-i-Martin (2004) simulate the Uzawa–Lucas model. I choose \(\mu =0.02\) and \(\delta _k=\delta _h=0.03\), again following Mankiw et al. (1992). Finally, following Caballé and Santos (1993) and Moll (2014), I set \(\rho =0.05\). In Fig. 1, I use \(K=10\) to make it transparent.

  8. I thank one anonymous referee for pointing out this property.

  9. One more marginal channel through which \(\mu \) increases A can be seen by solving the differential equation (3). However, this somewhat overlaps the first channel.

  10. I thank one anonymous referee for encouraging me to pursue this.

  11. Specifically, I use the solution to (1)

    $$\begin{aligned} H(t)=H(0)e^{\left( b(1-u)-\delta _h-\frac{\sigma _h^2}{2}\right) t}e^{\sigma _h z_h} \end{aligned}$$

    for simulation. Higham (2001) provides a concise explanation of simulation technique for stochastic differential equation driven by a Brownian motion process.

  12. According to Lee and Lee (2016) data set on human capital stock, we can also see the “bell-shaped” pattern in US between 2000 and 2005. During this period, the number declined from 3.708 (in 2000) to 3.673 (in 2005). In fact, this phenomenon is not unique in US. For instance, in Switzerland between 1980 and 2000, the number consecutively declined from 3.103 (in 1980) to 2.758 (in 2000); in Spain between 1915 and 1920, the number declined from 1.403 (in 1915) to 1.389 (in 1920); in Portugal between 2000 and 2005, the number declined from 2.318 (in 2000) to 2.253 (in 2005). These evidence suggests that the above exercise can be applied not only to the period of unprecedentedly big events (such as World War II) or to the specific country, but also to other (possibly) disruptive events across time and space.

  13. I thank one anonymous referee for pointing out this possibility.

  14. Steger (2005) compares a Brownian motion process with a Poisson jump process in the AK model. He shows that, to conduct a sensible comparison between these requires some unrealistic restrictions. Furthermore, even when they are imposed, he finds that insights from the comparison is quantitatively negligible. Following his findings, I will not do empirical simulation in what follows. In principle, with Poisson jump processes, we would see occasional jumps in Fig. 3, in addition to random fluctuations driven by a Brownian motion process.

  15. We can be sure that \(u\in (0,1)\) as long as the inequality

    $$\begin{aligned}&\alpha b-\alpha \delta _h-\frac{\sigma _h^2}{2}\alpha (1-\alpha )+\mu \gamma +\sum _{i=1}^N \lambda _i\left( (1+\beta _i)^{\alpha }-1\right)<\rho <b-\alpha \delta _h \end{aligned}$$
    $$\begin{aligned}&\quad -\frac{\sigma _h^2}{2}\alpha (1-\alpha )+\mu \gamma +\sum _{i=1}^N \lambda _i\left( (1+\beta _i)^{\alpha }-1\right) \end{aligned}$$
    (19)

    holds. Moreover, one can establish that the appropriate TVC is satisfied. Sennewald (2007) provides the proof of the TVC for the Poisson jump case.

  16. The notion of stochastic physical capital accumulation is first proposed by Eaton (1981). He assumes that the depreciation rate of physical capital follows a Brownian motion process. Similarly, Rebelo and Xie (1999) assume that it follows both a Brownian motion process and one Poisson process.

  17. We can be sure that \(u\in (0,1)\) as long as the inequality (19) holds. Moreover, one can establish that the appropriate TVC is satisfied. See Sennewald (2007) for the proof.

  18. See also Proposition 6 and 7 in Rebelo and Xie (1999) and Eq. (16) in Wälde (2011a).

  19. To be precise, as \(\mathcal {B}_X\) is contained in \(\mathcal {B}_Y\), shock terms in (22) affect both A and H, and hence welfare J. However, this channel would be too obvious to explain in detail.

References

  • Aghion P, Howitt P (1992) A model of growth through creative destruction. Econometrica 60(2):323–352

    Article  Google Scholar 

  • Ahn S, Kaplan G, Moll B, Winberry T, Wolf C (2017) When inequality matters for macro and macro matters for inequality. In: Eichenbaum MS, Parker J (eds) NBER macroeconomics annual 2017, vol 32. University of Chicago Press, Chicago

    Google Scholar 

  • Barro RJ, Sala-i-Martin X (2004) Economic growth, 2nd edn. MIT Press, Cambridge

    Google Scholar 

  • Bilkic N, Gries T, Pilichowski M (2012) Stay in school or start working? The human capital investment decision under uncertainty and irreversibility. Lab Econ 19:706–717

    Article  Google Scholar 

  • Brock WA, Mirman LJ (1972) Optimal economic growth and uncertainty: the discounted case. J Econ Theory 4(3):479–513

    Article  Google Scholar 

  • Brunnermeier MK, Sannikov Y (2014) A macroeconomic model with a financial sector. Am Econ Rev 104(2):379–421

    Article  Google Scholar 

  • Bucci A, Colapinto C, Forster M, La Torre D (2011) Stochastic technology shocks in an extended Uzawa–Lucas model: closed-form solution and long-run dynamics. J Econ 103(1):83–99

    Article  Google Scholar 

  • Caballé J, Santos MS (1993) On endogenous growth with physical and human capital. J Polit Econ 101(6):1042–1067

    Article  Google Scholar 

  • Chang F-R (2004) Stochastic optimization in continuous time. Cambridge University Press, New York

    Book  Google Scholar 

  • Chaudhry A, Naz R (2018) Closed-form solutions for the Lucas–Uzawa growth model with logarithmic utility preferences via the partial hamiltonian approach. Discret Contin Dyn Syst Ser S 11(4):643–654

    Google Scholar 

  • Cho J, Cooley TF, Kim SH (2015) Business cycle uncertainty and economic welfare. Rev Econ Dyn 18(2):185–200

    Article  Google Scholar 

  • Cinnirella F, Streb J (2017) The role of human capital and innovation in economic development: evidence from post-Malthusian Prussia. J Econ Growth 22(2):193–227

    Article  Google Scholar 

  • Duffie D, Epstein LG (1992) Stochastic differential utility. Econometrica 60(2):353–394

    Article  Google Scholar 

  • Eaton J (1981) Fiscal policy, inflation and the accumulation of risky capital. Rev Econ Stud 48(3):435–445

    Article  Google Scholar 

  • Hartog J, Ophem HV, Bajdechi SM (2007) Simulating the risk of investment in human capital. Educ Econ 15(3):259–275

    Article  Google Scholar 

  • Higham DJ (2001) An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev 43(3):525–546

    Article  Google Scholar 

  • Hiraguchi R (2009) A note on the closed-form solution to the Lucas–Uzawa model with externality. J Econ Dyn Control 33:1757–1760

    Article  Google Scholar 

  • Hiraguchi R (2013) On a closed-form solution to the stochastic Lucas–Uzawa model. J Econ 108(2):131–144

    Article  Google Scholar 

  • Hiraguchi R (2014) A note on the analytical solution to the neoclassical growth model with leisure. Macroecon Dyn 18(2):473–479

    Article  Google Scholar 

  • Hojo M (2003) An indirect effect of education on growth. Econ Lett 80:31–34

    Article  Google Scholar 

  • Karabarbounis L, Neiman B (2014) The global decline of the labor share. Q J Econ 129(1):61–103

    Article  Google Scholar 

  • Krebs T (2003) Human capital risk and economic growth. Q J Econ 118(3):709–744

    Article  Google Scholar 

  • Kuwahara S (2017) Multiple steady states and indeterminacy in the Uzawa–Lucas model with educational externalities. J Econ 122(2):173–190

    Article  Google Scholar 

  • Ladrón-De-Guevara A, Ortigueira S, Santos MS (1999) A two-sector model of endogenous growth with leisure. Rev Econ Stud 66(3):609–631

    Article  Google Scholar 

  • Lee JW, Lee H (2016) Human capital in the long run. J Dev Econ 122:147–169

    Article  Google Scholar 

  • Lester R, Pries M, Sims E (2014) Volatility and welfare. J Econ Dyn Control 38:17–36

    Article  Google Scholar 

  • Levhari D, Weiss Y (1974) The effect of risk on the investment in human capital. Am Econ Rev 64(6):950–963

    Google Scholar 

  • Lucas RE (1988) On the mechanics of economic development. J Monet Econ 22(1):3–42

    Article  Google Scholar 

  • Lucas RE (2003) Macroeconomic priorities. Am Econ Rev 93(1):1–14

    Article  Google Scholar 

  • Madsen JB (2014) Human capital and the world technology frontier. Rev Econ Stat 96(4):676–692

    Article  Google Scholar 

  • Mankiw NG, Romer D, Weil DN (1992) A contribution to the empirics of economic growth. Q J Econ 107(2):407–437

    Article  Google Scholar 

  • Marsiglio S, La Torre D (2012a) A note on demographic shocks in a multi-sector growth model. Econ Bull 32(3):2293–2299

    Google Scholar 

  • Marsiglio S, La Torre D (2012b) Population dynamics and utilitarian criteria in the Lucas–Uzawa model. Econ Model 29(4):1197–1204

    Article  Google Scholar 

  • Moll B (2014) Productivity losses from financial frictions: can self-financing undo capital misallocation? Am Econ Rev 104(10):3186–3221

    Article  Google Scholar 

  • Naz R, Chaudhry A, Mahomed FM (2016) Closed-form solutions for the Lucas–Uzawa model of economic growth via the partial Hamiltonian approach. Commun Nonlinear Sci Numer Simul 30:299–306

    Article  Google Scholar 

  • Rebelo S, Xie D (1999) On the optimality of interest rate smoothing. J Monet Econ 43(2):263–282

    Article  Google Scholar 

  • Sennewald K (2007) Controlled stochastic differential equations under Poisson uncertainty and with unbounded utility. J Econ Dyn Control 31(4):1106–1131

    Article  Google Scholar 

  • Sennewald K, Wälde K (2006) “Itô’s Lemma” and the Bellman equation for Poisson processes: an applied view. J Econ 89(1):1–36

    Article  Google Scholar 

  • Smith WT (2007) Inspecting the mechanism exactly: a closed-form solution to a stochastic growth model. BE J Macroecon 7(1):1–31

    Google Scholar 

  • Steger TM (2005) Stochastic growth under Wiener and Poisson uncertainty. Econ Lett 86:311–316

    Article  Google Scholar 

  • Turnovsky SJ (1997) International macroeconomic dynamics. MIT Press, Cambridge

    Google Scholar 

  • Turnovsky SJ (2000) Methods of macroeconomic dynamics, 2nd edn. MIT Press, Cambridge

    Google Scholar 

  • Uzawa H (1965) Optimum technical change in an aggregative model of economic growth. Int Econ Rev 6(1):18–31

    Article  Google Scholar 

  • Wälde K (2011a) Production technologies in stochastic continuous time models. J Econ Dyn Control 35(4):616–622

    Article  Google Scholar 

  • Wälde K (2011b) Applied intertemporal optimization. Mainz University Gutenberg Press, Mainz

    Google Scholar 

  • Xie D (1991) Increasing returns and increasing rates of growth. J Polit Econ 99(2):429–435

    Article  Google Scholar 

  • Xie D (1994) Divergence in economic performance: transitional dynamics with multiple equilibria. J Econ Theory 63(1):97–112

    Article  Google Scholar 

  • Xu S (2017) Volatility risk and economic welfare. J Econ Dyn Control 80:17–33

    Article  Google Scholar 

Download references

Acknowledgements

I thank Prof. Noritsugu Nakanishi, Assoc. Prof. Quoc Hung Nguyen, Prof. Hiroyuki Nishiyama, Prof. Masao Oda, Prof. Yoshifumi Okawa and seminar participants at the summer 2017 JSIE Kansai Branch Meeting for their many extensive and thoughtful comments. I would particularly like to thank Assoc. Prof. Shiro Kuwahara for his encouragement, pointing out troublesome typos, and constructive comments, “from the cradle to completion” of this paper. I am especially grateful to Prof. Yoichi Gokan, my discussant, and two anonymous referees of this journal for their detailed and exceptionally helpful comments that lead to the unthinkably substantial improvement of the earlier version of the manuscript. All remaining mistakes are my own. This paper was accepted to the J Econ under the guidance of Prof. Giacomo Corneo (Editor). Figure 2 is created with Eviews 9.5 Student Version, while the others are with MATLAB R2016b (Version 9.1, MATLAB and Simulink Student Suite). This research does not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Graduate School of Economics, University of Hyogo, 8-2-1, Nishi-Ku, Kobe, 651-2197, Japan

    Mizuki Tsuboi

Authors
  1. Mizuki Tsuboi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mizuki Tsuboi.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (m 3 KB)

Appendix: Analytical solution

Appendix: Analytical solution

This appendix briefly describes how to find the closed-form representation of the value function in Theorems 1, 2, and 3. For this purpose, postulate the tentative value function of the form

$$\begin{aligned} J(K,A,H)=x K^{\theta _1}+yA^{\theta _2}H^{\theta _3}+z \end{aligned}$$

where x, y, z, \(\theta _1\), \(\theta _2\), and \(\theta _3\) are all unknown constants to be determined. The relevant partials are \(J_K = x\theta _1 K^{\theta _1 -1}\), \(J_{KK} = x \theta _1(\theta _1 -1) K^{\theta _1-2}\), \(J_A = y \theta _2 A^{\theta _2 -1} H^{\theta _3}\), \(J_H = y \theta _3 A^{\theta _2} H^{\theta _3 -1}\), and \(J_{HH} = y \theta _3 (\theta _3-1) A^{\theta _2} H^{\theta _3 -2}\).

To obtain the explicit expression, substitute these partials into the maximized HJB equation (21). Then, set \(\theta _1=\alpha +\gamma \), \(\theta _2=\gamma \), and \(\theta _3=\alpha \). Finally, by imposing the parameter restriction (8), you can find the explicit expressions for x, y, and z, and consequently, those for control variables C and u and for the value function J(K, A, H) in Theorem 3. Expressions in Theorem 2 are available by abstracting from the shock terms associated with the stochastic depreciation of physical capital, while those in Theorem 1 are obtained by abstracting from many Poisson jump processes in Eq. (16).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tsuboi, M. Stochastic accumulation of human capital and welfare in the Uzawa–Lucas model: an analytical characterization. J Econ 125, 239–261 (2018). https://doi.org/10.1007/s00712-018-0604-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00712-018-0604-6

Keywords

JEL Classification

Search

Navigation