Productivity growth and welfare in a model of allocative inefficiency

Abstract

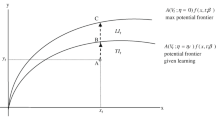
We develop a model of learning-by-doing in human capital formation in the presence of allocative inefficiencies. The inefficiencies are a result of lobbying by firms to establish, or prevent, barriers to the perfectly competitive allocation of factors of production (labor). It is shown that lobbying may lead to a static welfare loss depending upon the elasticity of substitution between goods, and the relative lobbying power of firms. Further, productivity growth, via learning by doing, changes the relative lobbying power over time. This may magnify or diminish the static welfare loss in the long-run depending on the level of initial misallocation. Therefore, differences in initial lobbying power and rate of productivity growth between sectors determine the long-run effects of lobbying.

Appendix

Proof

Proposition 1 Since the model features no physical capital, and maintaining Lucas’ assumption that human capital accumulation is external, the consumers in the model do not face any intertemporal trade-offs. Therefore, the consumer’s problem simplifies to maximizing utility given by

$$\begin{aligned} U = \left[ \alpha _{B} b^{-\gamma } + \alpha _{R}r^{-\gamma }\right] ^{-\frac{1}{\gamma }}. \end{aligned}$$

subject to a static income constraint. If P is the blue price of the red widgets, then utility maximization by an individual requires that P equals the marginal rate of substitution of reds for blue. Therefore, the optimality condition for the consumer’s maximization problem is

$$\begin{aligned} P = \frac{\partial {U}{/}\partial {r}}{\partial {U}{/}\partial {b}}. \end{aligned}$$

This yields the optimal consumption ratio as

$$\begin{aligned} \frac{r}{b} = \left( \frac{\alpha _{R}}{\alpha _{B}}\right) ^{\sigma } P^{-\sigma }. \end{aligned}$$

(16)

We have assumed that labor is free to move between the two types of firms, there is free entry into the production process, and learning effects are external to firms. In this case, all firms in the economy earn zero economic profits and all proceeds from production flow to labor. Under these assumptions profit maximization implies that the relative price under perfect competition is equal to the marginal rate of transformation. That is,

$$\begin{aligned} P = \frac{h_{B}}{h_{R}}\equiv P_{C}, \end{aligned}$$

(17)

Imposing the condition that at $P_{C}$, market for blue and red widget clears, Eq. (16) becomes

$$\begin{aligned} \frac{(1-\lambda )h_{R}}{\lambda h_{B}} = \left( \frac{\alpha _{R}}{\alpha _{B}}\right) ^{\sigma } P_{C}^{-\sigma }, \end{aligned}$$

which combined with Eq. (17) yields

$$\begin{aligned} \lambda = \frac{1}{1+ \left( \frac{\alpha _{R}}{\alpha _{B}}\right) ^{\sigma } P_{C}^{1 - \sigma }} \equiv \lambda _{C}. \end{aligned}$$

$\square$

Proof

Proposition 2 We solve this problem using backward induction wherein type R firms decide on the optimal $\rho$ for a given $\beta$. Type B firms use this information to decide their optimal contribution of resources. As is clear from (10), in the interval $[0, \theta \beta ]$ the output of type R firms is constant and therefore the payoff decreases in $\rho$. Therefore, over this interval the optimal contribution of type R firms is $\rho ^{*} = 0$. Thus for an interior solution with $\rho > 0$, we must have $\rho \in (\theta \beta , \infty )$. The necessary condition for type R firms to expend an amount $\rho > \theta \beta$ is that the payoff must be rising at the the cutoff point $\theta \beta$. That is, the first derivative of the payoff function with respect to $\rho$ evaluated at $\theta \beta$ must be positive. This requires that

$$\begin{aligned} \beta < (\lambda _{C}h_{R})/\theta \equiv \tilde{\beta }. \end{aligned}$$

(18)

Assuming this condition holds, one finds that the payoff function of type R firms in the interval $(\theta \beta , \infty )$ is $[ 1 - (\theta \beta / \rho )\lambda _{C}]h_{R} - \rho$, which is maximized at

$$\begin{aligned} \rho = (\theta \beta \lambda _{C}h_{R})^{1/2}. \end{aligned}$$

(19)

However, this value of $\rho$ is optimal if and only if the payoff at $\rho = (\theta \beta \lambda _{C}h_{R})^{1/2}$ is greater than the payoff obtained when $\rho = 0$. This requires

$$\begin{aligned} \beta < (\lambda _{C}h_{R})/4\theta \equiv \hat{\beta }. \end{aligned}$$

(20)

Note that if (20) is satisfied then (18) also holds, since $\tilde{\beta } < \hat{\beta }$. This establishes that the optimal value for $\rho$, $\rho ^{*}$, is

$$\begin{aligned} \rho ^{*} = 0,\quad \textit{if}~\beta \ge \hat{\beta }\equiv (\lambda _{C}h_{R})/4\theta , \rho ^{*} = (\theta \beta \lambda _{C}h_{R})^{1/2},\quad \textit{if}~\beta < \hat{\beta }. \end{aligned}$$

(21)

Given the values for $\rho ^{*}$ in Eq. (21), we can now determine the optimal allocation for the type B leader. As apparent from Eq. (21), the optimal value for $\beta$ lies in the interval $[0, \hat{\beta }\equiv (\lambda _{C}h_{R})/4\theta ]$. Given Eq. (21), the payoff function for the type B firms is

$$\begin{aligned} \pi _{B} = \left\{ \begin{array}{ll}(\theta \beta \lambda _{C})^{1/2}h_{B} / h_{R}^{1/2} - \beta &{} \quad \text {if}~\beta < \hat{\beta } \\ \lambda _{C}h_{B}-\hat{\beta } &{} \quad \text {if}~\beta = \hat{\beta }\end{array}\right. \end{aligned}$$

Let $f(\beta ) \equiv (\theta \beta \lambda _{C})^{1/2} h_{B}/ h_{R}^{1/2} - \beta$ and note that $f'(\beta ) >,<$, or $= 0$, as $\beta <, >,$ or $= \beta ^{*} \equiv (\theta \lambda _{C}h_{B}^{2})/4 h_{R}$. From these facts it follows that $\pi _{B}$ is maximized at $\hat{\beta }$, if $\hat{\beta } \equiv (\lambda _{C}h_{R})/4\theta \le \beta ^{*} \equiv (\theta \lambda _{C}h_{B}^{2})/4 h_{R}$, that is, if $\theta \ge (h_{R} / h_{B})$.

Suppose $\theta < (h_{R} / h_{B})$ and thus $\beta ^{*}$ is less than $\hat{\beta }$. Then in this case $f'(\beta ) = 0$ at $\beta = \beta ^{*}\in [0,\hat{\beta })$ and therefore $\beta ^{*}$ is a candidate optimal value for $\beta$. We say candidate because it still may pay the type B firms to generate a discrete jump in $\pi _{B}$ by increasing $\beta$ from $\beta ^{*}$ to $\hat{\beta }$.

Note that if $\beta = \beta ^{*} \equiv (\theta \lambda _{C}h_{B}^{2})/4 h_{R}$ then $z^{*} \equiv (\theta /2) (h_{B}/h_{R})$ and the payoff to the type B firms is $\pi _{B}(\beta ^{*}) = (\theta \lambda _{C} h_{B}^{2})/2h_{R} - (\theta \lambda _{C} h_{B}^{2})/4h_{R} = (\theta \lambda _{C} h_{B}^{2})/4h_{R}$. However, this must be compared to $\pi _{B}(\hat{\beta }) = h_{B}\lambda _{C} - (\lambda _{C}h_{R})/4\theta$. One finds that when $\beta ^{*} < \hat{\beta }$,

$$\begin{aligned} \pi _{B}(\beta ^{*}) - \pi _{B}(\hat{\beta })>,< or = 0\ as \ g(\theta ) \equiv \theta ^{2}h_{B}^{2} - 4 h_{R}h_{B}\theta + h_{R}^{2} >, <, or = 0. \end{aligned}$$

The quadratic function $g(\theta )$ has zeros at $\theta = (h_{R}/h_{B})(2 - \sqrt{3})$ and $\theta = (h_{R}/h_{B})(2 + \sqrt{3})$ and is negative on the interval $(h_{R}/h_{B})(2 - \sqrt{3}), (h_{R}/h_{B})(2 + \sqrt{3}))$. Thus on this interval the optimal value for $\beta$ is $\hat{\beta }$. When $\theta < \theta _{C} \equiv (h_{R}/h_{B})(2 - \sqrt{3})$, the optimal value is $\beta ^{*}$ and we have an interior solution with $z^{*} < 1$. When $\theta > (h_{R}/h_{B})(2 + \sqrt{3})$, $\theta > (h_{R}/h_{B})$, and our previous analysis has established that the optimal value is $\hat{\beta }$ $\square$