Continuous contact problem of interaction between two arbitrarily positioned flat stamps on the thermoelectric material

Abstract

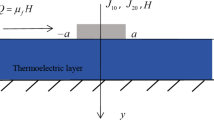
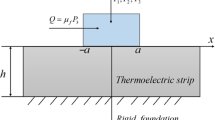
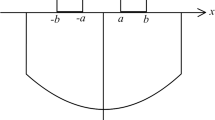
A continuous contact model of the thermoelectric layer under the action of two arbitrarily flat stamps is established. By using Fourier integral transformation method, the singular integral equations of the contact problem under different flat stamps are obtained. The contact stress distribution between two arbitrary stamps and the thermoelectric layer is given by using the numerical method for solving the singular integral equation. The influence of the interaction between two stamps on the current energy flow and the stress distribution in the thermoelectric material is discussed. The results show that when the stamps are close to each other, the thermoelectric layer and the rigid substrate are easier to fall off. The obtained research results can give the stress distribution of thermoelectric materials at any stamp position, and the model can also be degenerated into the contact problem under double symmetry or single stamp.

Appendices

Appendix A

$$N_{1} (x,y) = N_{d1} (x,y) + N_{d2} (x,y)$$

$$N_{2} (x,y) = N_{f1} (x,y) + N_{f2} (x,y)$$

$$\begin{gathered} N_{d1} (x,y) = \frac{G}{k - 1}\left( {(k + 1)\left( {\frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left( { - \frac{{i\beta^{*} \gamma }}{\pi \lambda (\kappa - 1)}\int\limits_{ - \infty }^{\infty } {(\eta_{1} X_{1} I_{1} (\xi )I_{1} (s - \xi )e^{{\eta_{1} y}} + \eta_{2} X_{2} I_{2} (\xi )I_{2} (s - \xi )e^{{\eta_{2} y}} } } \right.} } \right.} \right. \hfill \\ \quad \quad \quad \quad \quad \left. {\left. {\left. { +\, \eta_{3} X_{3} I_{1} (s - \xi )I_{2} (\xi )e^{{\eta_{3} y}} + \eta_{4} X_{4} I_{1} (\xi )I_{2} (s - \xi )e^{{\eta_{4} y}} } \right)d\xi - \left| s \right|X_{5} H_{1} (s)e^{ - \left| s \right|y} + \left| s \right|X_{6} H_{2} (s)e^{\left| s \right|y} } \vphantom{\int\limits_{ - \infty }^{\infty }}\right)e^{ - isx} ds} \vphantom{\int\limits_{ - \infty }^{\infty }}\right) \hfill \\ \quad \quad \quad \quad \quad + \,(3 - k)\left( {\frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left( {s\frac{{\beta^{*} \gamma }}{\pi \lambda (\kappa - 1)}\int\limits_{ - \infty }^{\infty } {\left( {K_{1} I_{1} (\xi )I_{1} (s - \xi )e^{{\eta_{1} y}} + K_{2} I_{2} (\xi )I_{2} (s - \xi )e^{{\eta_{2} y}} } \right.} } \right.} } \right. \hfill \\ \quad \quad \quad \quad \quad \left. {\left. {\left. { +\, K_{3} I_{1} (s - \xi )I_{2} (\xi )e^{{\eta_{3} y}} + K_{4} I_{1} (\xi )I_{2} (s - \xi )e^{{\eta_{4} y}} )d\xi + \left( {K_{5} H_{1} (s)e^{ - \left| s \right|y} + K_{6} H_{2} (s)e^{\left| s \right|y} } \right)} \vphantom{\int\limits_{ - \infty }^{\infty }}\right)e^{ - isx} ds}\vphantom{\int\limits_{ - \infty }^{\infty }} \right)} \vphantom{\int\limits_{ - \infty }^{\infty }}\right) \hfill \\ \end{gathered}$$

(A.1)

$$N_{d2} (x,y) = - \rho g( - y + h)$$

(A.2)

$$\begin{gathered} N_{f1} (x,y) = G\left( {\frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left( {\frac{{i\beta^{*} \gamma }}{\pi \lambda (\kappa - 1)}\int\limits_{ - \infty }^{\infty } {\left( {\eta_{1} K_{1} I_{1} (\xi )I_{1} (s - \xi )e^{{\eta_{1} y}} + \eta_{2} K_{2} I_{2} (\xi )I_{2} (s - \xi )e^{{\eta_{2} y}} } \right.} } \right.} } \right. \hfill \\ \quad \quad \quad \quad \quad \left. {\left. {\left. { +\, \eta_{3} K_{3} I_{1} (s - \xi )I_{2} (\xi )e^{{\eta_{3} y}} + \eta_{4} K_{4} I_{1} (\xi )I_{2} (s - \xi )e^{{\eta_{4} y}} } \right)d\xi + \left( { - \left| s \right|K_{5} H_{1} (s)e^{ - \left| s \right|y} + \left| s \right|K_{6} H_{2} (s)e^{\left| s \right|y} } \right)} \vphantom{\int\limits_{ - \infty }^{\infty }} \right)e^{ - isx} ds} \vphantom{\int\limits_{ - \infty }^{\infty }}\right) \hfill \\ \quad \quad \quad \quad \quad +\, \left( {\frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left( { - s\frac{{\beta^{*} \gamma }}{\pi \lambda (\kappa - 1)}\int\limits_{ - \infty }^{\infty } {\left( {X_{1} I_{1} (\xi )I_{1} (s - \xi )e^{{\eta_{1} y}} + X_{2} I_{2} (\xi )I_{2} (s - \xi )e^{{\eta_{2} y}} } \right.} } \right.} } \right. \hfill \\ \quad \quad \quad \quad \quad \left. {\left. { +\, X_{3} I_{1} (s - \xi )I_{2} (\xi )e^{{\eta_{3} y}} + X_{4} I_{1} (\xi )I_{2} (s - \xi )e^{{\eta_{4} y}} )d\xi + X_{5} H_{1} (s)e^{ - \left| s \right|y} + X_{6} H_{2} (s)e^{\left| s \right|y} } \vphantom{\int\limits_{ - \infty }^{\infty }}\right)e^{ - isx} ds} \vphantom{\int\limits_{ - \infty }^{\infty }}\right) \hfill \\ \end{gathered}$$

(A.3)

$$N_{d2} (x,y) = 0$$

(A.4)

Appendix B

$$K_{11} (x_{1} ) = \frac{1}{\pi }\int\limits_{a}^{b} {\left( {M_{1} (r_{1} ,x_{1} ) + \frac{1}{{r_{1} - x_{1} }}} \right)dr}$$

(B.1.1)

$$K_{12} (x_{1} ) = \frac{1}{\pi }\int\limits_{c}^{d} {\left(M_{1} (r_{2} ,x_{1} ) + \frac{1}{{r_{2} - x_{1} }}\right)dr_{2} }$$

(B.1.2)

$$K_{21} (x_{2} ) = \frac{1}{\pi }\int\limits_{a}^{b} {\left(M_{1} (r_{1} ,x_{2} ) + \frac{1}{{r_{1} - x_{2} }}\right)dr_{1} }$$

(B.1.3)

$$K_{22} (x_{2} ) = \frac{1}{\pi }\int\limits_{c}^{d} {\left(M_{1} (r_{2} ,x_{2} ) + \frac{1}{{r_{2} - x_{2} }}\right)dr_{2} }$$

(B.1.4)

$$L_{11} (x_{1} ) = \frac{1}{\pi }\int\limits_{a}^{b} {\left(M_{2} (r_{1} ,x_{1} ) + \frac{k - 1}{{4G}}\frac{1}{{r_{1} - x_{1} }}\right)dr_{1} }$$

(B.2.1)

$$L_{12} (x_{1} ) = \frac{1}{\pi }\int\limits_{c}^{d} {\left(M_{2} (r_{2} ,x_{1} ) + \frac{k - 1}{{4G}}\frac{1}{{r_{2} - x_{1} }}\right)dr_{2} }$$

(B.2.2)

$$L_{21} (x_{2} ) = \frac{1}{\pi }\int\limits_{a}^{b} {\left(M_{2} (r_{1} ,x_{2} ) + \frac{k - 1}{{4G}}\frac{1}{{r_{1} - x_{2} }}\right)dr_{1} }$$

(B.2.3)

$$L_{22} (x_{2} ) = \frac{1}{\pi }\int\limits_{c}^{d} {\left(M_{2} (r_{2} ,x_{2} ) + \frac{k - 1}{{4G}}\frac{1}{{r_{2} - x_{2} }}\right)dr_{2} }$$

(B.2.4)

$$M_{1} (r,x) = \int\limits_{ - \infty }^{\infty } {\left(\frac{{1 - e^{ - 2\left| s \right|h} }}{{1 + e^{ - 2\left| s \right|h} }} - 1\right)\sin (s(r - x))ds}$$

(B.3)

$$M_{2} (r,x) = \int\limits_{0}^{\infty } \left( - \frac{{(k + 1)(2{\text{e}}^{ - 2sh} - 1 - {\text{e}}^{ - 4sh} )}}{{4(4sh{\text{e}}^{ - 2sh} + 1 - {\text{e}}^{ - 4sh} )G}} - \frac{(k + 1)}{{4G}}\right)\sin (s(r - x))ds$$

(B.4)

Appendix C

$$N_{11} = \frac{{ - i(2|s|{\text{e}}^{2|s|h} h - {\text{e}}^{2|s|h} k + 2|s|h + {\text{e}}^{2|s|h} + k - 1){\text{e}}^{|s|h} }}{{2G(4|s|{\text{e}}^{2|s|h} h + {\text{e}}^{4|s|h} - 1)s}}$$

(C.1)

$$N_{12} = \frac{{(2|s|h - k - 1){\text{e}}^{3|s|h} + ( - 2|s|h - k - 1){\text{e}}^{|s|h} }}{{2G|s|(4|s|{\text{e}}^{2|s|h} h + {\text{e}}^{4|s|h} - 1)}}$$

(C.2)

$$N_{21} = \frac{{2{\text{e}}^{|s|h} ((|s|h + 1){\text{e}}^{2|s|h} + |s|h - 1)}}{{4|s|{\text{e}}^{2|s|h} h + {\text{e}}^{4|s|h} - 1}}$$

(C.3)

$$N_{22} = \frac{{2{\mkern 1mu} {\text{i}}sh({\text{e}}^{2|s|h} - 1){\text{e}}^{|s|h} }}{{4|s|{\text{e}}^{2|s|h} h + {\text{e}}^{4|s|h} - 1}}$$

(C.4)