Skip to main content
SpringerLink
Log in

Representative volume element model of triply periodic minimal surfaces (TPMS)-based electrostrictive composites for numerical evaluation of effective properties

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

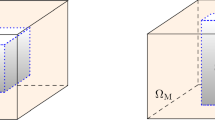
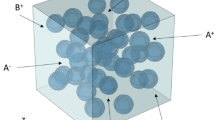
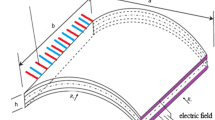
A model for numerical homogenization of triply periodic minimal surfaces (TPMS) based on electrostrictive composites is presented. This electrostrictive composite consists of TPMS (a three-dimensional continuous structure) implanted in a soft non-electrostrictive matrix. A representative volume element (RVE)-based approach is used to homogenize the electrostrictive composites and determine all the effective electrostrictive, mechanical, and electrical coefficients. Finite element formulation is employed to solve the nonlinear electrostrictive constitutive equations. Special attention is paid to designing the boundary conditions that permit the fast calculation based on simulations of overall deformation-induced due to mechanical and electrical loads. Interestingly, the value of the effective electrostrictive coefficient of the composite surpasses that of the inclusion Pb (mg1/3Nb2/3)O3-PbTO3-BaTiO3 (PMN-PT-BT), even though the matrix is non-electrostrictive due to the additional flexibility imparted by the matrix. This electrostrictive response of TPMS-based composite is independent of the type of TPMS structures used. It is prudent to say that these composites will find their place in practical application owing to their salient features of more flexibility and high electrostrictive coefficient.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Zhuang, X., Nguyen, C., Nanthakumar, S.S., Chamoin, L., Jin, Y., Rabczuk, T.: Inverse design of reconfigurable piezoelectric topological phononic plates. Mater. Des. 219 110760 (2022)

    Article  Google Scholar 

  2. Mortazavi, B., Shojaei, F., Javvaji, B., Rabczuk, T., Zhuang, X.: Outstandingly high thermal conductivity, elastic modulus, carrier mobility and piezoelectricity in two-dimensional semiconducting CrC2N4: a first-principles study. Mater. Today Energy. 22, 100839 (2021)

    Article  Google Scholar 

  3. Ghasemi, H., Park, H.S., Rabczuk, T.: A multi-material level set-based topology optimization of flexoelectric composites. Comput. Methods Appl. Mech. Eng. 332, 47–62 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  4. Ghasemi, H., Park, H.S., Zhuang, X., Rabczuk, T.: Three-dimensional isogeometric analysis of flexoelectricity with MATLAB implementation. Comput. Mater. Contin. 65, 1157–1179 (2020)

    Google Scholar 

  5. Hamdia, K.M., Ghasemi, H., Zhuang, X., Rabczuk, T.: Multilevel Monte Carlo method for topology optimization of flexoelectric composites with uncertain material properties. Eng. Anal. Bound. Elem. 134, 412–418 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  6. Sharma, S., Kumar, R., Talha, M., Vaish, R.: Flexoelectric poling of functionally graded ferroelectric materials. Adv. Theory Simul. 4, 2000158 (2021)

    Article  Google Scholar 

  7. Diguet, G., Cavaille, J.-Y., Sebald, G., Takagi, T., Yabu, H., Suzuki, A., Miura, R.: Physical behavior of electrostrictive polymers. Part 1: Polarization forces. Comput. Mater. Sci. 190, 110294 (2021)

    Article  Google Scholar 

  8. Tohluebaji, N., Thainiramit, P., Putson, C., Muensit, N.: Phase and structure behavior vs. electromechanical performance of electrostrictive P (VDF-HFP)/ZnO composite nanofibers. Polymers (Basel) 13, 2565 (2021)

  9. Farhan, R., Eddiai, A., Meddad, M., Chakhchaoui, N., Rguiti, M., Mazroui, M.: Improvement in energy conversion of electrostrictive composite materials by new approach via piezoelectric effect: modeling and experiments. Polym. Adv. Technol. 32, 123–130 (2021)

    Article  Google Scholar 

  10. Sundar, V., Newnham, R.E.: Electrostriction and polarization. Ferroelectrics 135, 431–446 (1992)

    Article  Google Scholar 

  11. Hom, C.L., Shankar, N.: A fully coupled constitutive model for electrostrictive ceramic materials. J. Intell. Mater. Syst. Struct. 5, 795–801 (1994)

    Article  Google Scholar 

  12. Hom, C.L., Shankar, N.: A finite element method for electrostrictive ceramic devices. Int. J. Solids Struct. 33, 1757–1779 (1996). https://doi.org/10.1016/0020-7683(95)00123-9

    Article  MATH  Google Scholar 

  13. Bai, Y., Cheng, Z.-Y., Bharti, V., Xu, H.S., Zhang, Q.M.: High-dielectric-constant ceramic-powder polymer composites. Appl. Phys. Lett. 76, 3804–3806 (2000)

    Article  Google Scholar 

  14. Wang, J.J., Meng, F.Y., Ma, X.Q., Xu, M.X., Chen, L.Q.: Lattice, elastic, polarization, and electrostrictive properties of BaTiO 3 from first-principles. J. Appl. Phys. 108, 34107 (2010)

    Article  Google Scholar 

  15. Tang, T., Yu, W.: Effective nonlinear behavior of electrostrictive multiphase composites: a micromechanical study. Int. J. Eng. Sci. 48, 1769–1777 (2010)

    Article  MATH  Google Scholar 

  16. Farhan, R., Eddiai, A., Meddad, M., Mazroui, M., Guyomar, D.: Electromechanical losses evaluation by energy-efficient method using the electrostrictive composites: experiments and modeling. Smart Mater. Struct. 28, 35024 (2019)

    Article  Google Scholar 

  17. Li, J.Y.: The effective electroelastic moduli of textured piezoelectric polycrystalline aggregates. J. Mech. Phys. Solids 48, 529–552 (2000)

    Article  MATH  Google Scholar 

  18. Fang, D.-N., Jiang, B., Hwang, K.-C.: A model for predicting effective properties of piezocomposites with non-piezoelectric inclusions. J. Elast. Phys. Sci. Solids. 62, 95–118 (2001)

    MATH  Google Scholar 

  19. Sabina, F.J., Rodrı́guez-Ramos, R., Bravo-Castillero, J., Guinovart-Dı́az, R.: Closed-form expressions for the effective coefficients of a fibre-reinforced composite with transversely isotropic constituents. II: Piezoelectric and hexagonal symmetry. J. Mech. Phys. Solids. 49, 1463–1479 (2001)

  20. Aboudi, J.: Micromechanical prediction of the effective coefficients of thermo-piezoelectric multiphase composites. J. Intell. Mater. Syst. Struct. 9, 713–722 (1998)

    Article  Google Scholar 

  21. Castaneda, P.P., Suquet, P.: Nonlinear composites. Adv. Appl. Mech. 34, 171–302 (1997)

    Article  MATH  Google Scholar 

  22. Castañeda, P.P.: Exact second-order estimates for the effective mechanical properties of nonlinear composite materials. J. Mech. Phys. Solids. 44, 827–862 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  23. Willis, J.R.: On methods for bounding the overall properties of nonlinear composites. J. Mech. Phys. Solids 39, 73–86 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  24. Talbot, D.R.S., Willis, J.R.: Three-point bounds for the overall properties of a nonlinear composite dielectric. IMA J. Appl. Math. 57, 41–52 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  25. Guillot, F.M., Jarzynski, J., Balizer, E.: Measurement of electrostrictive coefficients of polymer films. J. Acoust. Soc. Am. 110, 2980–2990 (2001)

    Article  Google Scholar 

  26. Li, J., Rao, N.: Micromechanics of ferroelectric polymer-based electrostrictive composites. J. Mech. Phys. Solids 52, 591–615 (2004)

    Article  MATH  Google Scholar 

  27. Lebrun, L., Guyomar, D., Guiffard, B., Cottinet, P.-J., Putson, C.: The Characterisation of the harvesting capabilities of an electrostrictive polymer composite. Sens Actuators A Phys. 153, 251–257 (2009)

    Article  Google Scholar 

  28. Li, S., Xiong, D., Liu, M., Bai, S., Zhao, X.: Thermophysical properties of SiC/Al composites with three dimensional interpenetrating network structure. Ceram. Int. 40, 7539–7544 (2014)

    Article  Google Scholar 

  29. Cheng, F., Kim, S.-M., Reddy, J.N., Al-Rub, R.K.A.: Modeling of elastoplastic behavior of stainless-steel/bronze interpenetrating phase composites with damage evolution. Int. J. Plast. 61, 94–111 (2014)

    Article  Google Scholar 

  30. Poniznik, Z., Salit, V., Basista, M., Gross, D.: Effective elastic properties of interpenetrating phase composites. Comput. Mater. Sci. 44, 813–820 (2008)

    Article  Google Scholar 

  31. Al-Ketan, O., Abu Al-Rub, R.K.: Multifunctional mechanical metamaterials based on triply periodic minimal surface lattices. Adv. Eng. Mater. 21, 1900524 (2019)

    Article  Google Scholar 

  32. Al-Ketan, O., Lee, D.-W., Rowshan, R., Al-Rub, R.K.A.: Functionally graded and multi-morphology sheet TPMS lattices: design, manufacturing, and mechanical properties. J. Mech. Behav. Biomed. Mater. 102, 103520 (2020)

    Article  Google Scholar 

  33. Yang, N., Quan, Z., Zhang, D., Tian, Y.: Multi-morphology transition hybridization CAD design of minimal surface porous structures for use in tissue engineering. Comput. Des. 56, 11–21 (2014)

    Google Scholar 

  34. Yang, N., Du, C., Wang, S., Yang, Y., Zhang, C.: Mathematically defined gradient porous materials. Mater. Lett. 173, 136–140 (2016)

    Article  Google Scholar 

  35. Yin, H., Liu, Z., Dai, J., Wen, G., Zhang, C.: Crushing behavior and optimization of sheet-based 3D periodic cellular structures. Compos. Part B Eng. 182, 107565 (2020)

    Article  Google Scholar 

  36. Abueidda, D.W., Dalaq, A.S., Al-Rub, R.K.A., Younes, H.A.: Finite element predictions of effective multifunctional properties of interpenetrating phase composites with novel triply periodic solid shell architectured reinforcements. Int. J. Mech. Sci. 92, 80–89 (2015)

    Article  Google Scholar 

  37. Dalaq, A.S., Abueidda, D.W., Al-Rub, R.K.A., Jasiuk, I.M.: Finite element prediction of effective elastic properties of interpenetrating phase composites with architectured 3D sheet reinforcements. Int. J. Solids Struct. 83, 169–182 (2016)

    Article  Google Scholar 

  38. Dalaq, A.S., Abueidda, D.W., Al-Rub, R.K.A.: Mechanical properties of 3D printed interpenetrating phase composites with novel architectured 3D solid-sheet reinforcements. Compos. Part A Appl. Sci. Manuf. 84, 266–280 (2016)

    Article  Google Scholar 

  39. Al-Rub, R.K.A., Abueidda, D.W., Dalaq, A.S.: Thermo-electro-mechanical properties of interpenetrating phase composites with periodic architectured reinforcements. In: From Creep Damage Mechanics to Homogenization Methods, pp. 1–18. Springer (2015)

  40. Wang, L., Lau, J., Thomas, E.L., Boyce, M.C.: Co-continuous composite materials for stiffness, strength, and energy dissipation. Adv. Mater. 23, 1524–1529 (2011)

    Article  Google Scholar 

  41. Abueidda, D.W., Dalaq, A.S., Al-Rub, R.K.A., Jasiuk, I.: Micromechanical finite element predictions of a reduced coefficient of thermal expansion for 3D periodic architectured interpenetrating phase composites. Compos. Struct. 133, 85–97 (2015)

    Article  Google Scholar 

  42. Abueidda, D.W., Al-Rub, R.K.A., Dalaq, A.S., Younes, H.A., Al Ghaferi, A.A., Shah, T.K.: Electrical conductivity of 3D periodic architectured interpenetrating phase composites with carbon nanostructured-epoxy reinforcements. Compos. Sci. Technol. 118, 127–134 (2015)

  43. Abueidda, D.W., Al-Rub, R.K.A., Dalaq, A.S., Lee, D.-W., Khan, K.A., Jasiuk, I.: Effective conductivities and elastic moduli of novel foams with triply periodic minimal surfaces. Mech. Mater. 95, 102–115 (2016)

    Article  Google Scholar 

  44. Gandy, P.J.F., Bardhan, S., Mackay, A.L., Klinowski, J.: Nodal surface approximations to the P, G, D and I-WP triply periodic minimal surfaces. Chem. Phys. Lett. 336, 187–195 (2001)

    Article  Google Scholar 

  45. Brakke, K.A.: The surface evolver. Exp. Math. 1, 141–165 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  46. Novak, N., Al-Ketan, O., Krstulović-Opara, L., Rowshan, R., Al-Rub, R.K.A., Vesenjak, M., Ren, Z.: Quasi-static and dynamic compressive behaviour of sheet TPMS cellular structures. Compos. Struct. 266, 113801 (2021)

    Article  Google Scholar 

  47. Xu, H., Xie, Y.M., Chan, R., Zhou, S.: Piezoelectric properties of triply periodic minimum surface structures. Compos. Sci. Technol. 200, 108417 (2020)

    Article  Google Scholar 

  48. Debus, J.-C., Dubus, B., Coutte, J.: Finite element modeling of lead magnesium niobate electrostrictive materials: static analysis. J. Acoust. Soc. Am. 103, 3336–3343 (1998)

    Article  Google Scholar 

  49. Devonshire, A.F.: Theory of ferroelectrics. Adv. Phys. 3, 85–130 (1954)

    Article  MATH  Google Scholar 

  50. Suo, Z.: Mechanics concepts for failure in ferroelectric ceramics. Smart Struct. Mater. 112, 1–6 (1991)

    Google Scholar 

  51. Suquet, P.: Elements of homogenization theory for inelastic solid mechanics. In: Sanchez-Palencia, E., Zaoui, A. (eds.) Homogenization Techniques for Composite Media, pp. 194–278 (1987)

    Google Scholar 

  52. Powers, J.M., McLaughlin, E.A., Moffett, M.B.: PMN measurements at NUWC. NUWC Report, 918 (1995)

  53. Hom, C.L., Pilgrim, S.M., Shankar, N., Bridger, K., Massuda, M., Winzer, S.R.: Calculation of quasi-static electromechanical coupling coefficients for electrostrictive ceramic materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 41, 542–551 (1994)

    Article  Google Scholar 

  54. McLaughlin, E.A., Powers, J.M., Moffett, M.B., Janus, R.S.: Characterization of PMN‐PT‐La for use in high‐power electrostrictive projectors. 100, 2729 (1996)

  55. Berger, H., Kari, S., Gabbert, U., Rodriguez-Ramos, R., Bravo-Castillero, J., Guinovart-Diaz, R., Sabina, F.J., Maugin, G.A.: Unit cell models of piezoelectric fiber composites for numerical and analytical calculation of effective properties. Smart Mater. Struct. 15, 451 (2006)

    Article  Google Scholar 

  56. Van den Ende, D.A., Bory, B.F., Groen, W.A., Van Der Zwaag, S.: Properties of quasi 1–3 piezoelectric PZT-epoxy composites obtained by dielectrophoresis. Integr. Ferroelectr. 114, 108–118 (2010)

    Article  Google Scholar 

  57. Eury, S., Yimnirun, R., Sundar, V., Moses, P.J., Jang, S.-J., Newnham, R.E.: Converse electrostriction in polymers and composites. Mater. Chem. Phys. 61, 18–23 (1999)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Engineering, Indian Institute of Technology Mandi, Himachal Pradesh, Mandi, 175075, India

    Diwakar Singh, Saurav Sharma, Rajeev Kumar & Rahul Vaish

  2. Faculty of Mechanical, Maritime and Materials Engineering, Delft University of Technology, Mekelweg 2, 2628 CD, Delft, The Netherlands

    Saurav Sharma

Authors
  1. Diwakar Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Saurav Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Rajeev Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Rahul Vaish
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Diwakar Singh.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A

Appendix A

Shape function \({N}_{i}\) for linear tetrahedral element is

$${N}_{i}=\frac{\left({\alpha }_{i}+{\beta }_{i}{x}_{1}+{\gamma }_{i}{x}_{2}+{\delta }_{i}{x}_{3}\right)}{6V},$$
(A.1)

where i varies from 1 to 4, and

$${\alpha }_{1}=\left|\begin{array}{c}{x}_{1}^{2}\\ {x}_{1}^{3}\\ {x}_{1}^{4}\end{array} \begin{array}{c}{x}_{2}^{2}\\ {x}_{2}^{3}\\ {x}_{2}^{4}\end{array} \begin{array}{c}{x}_{3}^{2}\\ {x}_{3}^{3}\\ {x}_{3}^{4}\end{array}\right|, {\beta }_{1}=-\left|\begin{array}{c}1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{2}^{2}\\ {x}_{2}^{3}\\ {x}_{2}^{4}\end{array} \begin{array}{c}{x}_{3}^{2}\\ {x}_{3}^{3}\\ {x}_{3}^{4}\end{array}\right|, {\gamma }_{1}=\left|\begin{array}{c}1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{1}^{2}\\ {x}_{1}^{3}\\ {x}_{1}^{4}\end{array} \begin{array}{c}{x}_{3}^{2}\\ {x}_{3}^{3}\\ {x}_{3}^{4}\end{array}\right|, {\delta }_{1}=-\left|\begin{array}{c}1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{1}^{2}\\ {x}_{1}^{3}\\ {x}_{1}^{4}\end{array} \begin{array}{c}{x}_{2}^{2}\\ {x}_{2}^{3}\\ {x}_{2}^{4}\end{array}\right|,$$
(A.2)
$${\alpha }_{2}=-\left|\begin{array}{c}{x}_{1}^{1}\\ {x}_{1}^{3}\\ {x}_{1}^{4}\end{array} \begin{array}{c}{x}_{2}^{1}\\ {x}_{2}^{3}\\ {x}_{2}^{4}\end{array} \begin{array}{c}{x}_{3}^{1}\\ {x}_{3}^{3}\\ {x}_{3}^{4}\end{array}\right|, {\beta }_{2}=\left|\begin{array}{c}1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{2}^{1}\\ {x}_{2}^{3}\\ {x}_{2}^{4}\end{array} \begin{array}{c}{x}_{3}^{1}\\ {x}_{3}^{3}\\ {x}_{3}^{4}\end{array}\right|, {\gamma }_{2}=-\left|\begin{array}{c}1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{1}^{1}\\ {x}_{1}^{3}\\ {x}_{1}^{4}\end{array} \begin{array}{c}{x}_{3}^{1}\\ {x}_{3}^{3}\\ {x}_{3}^{4}\end{array}\right|, {\delta }_{2}=\left|\begin{array}{c}1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{1}^{1}\\ {x}_{1}^{3}\\ {x}_{1}^{4}\end{array} \begin{array}{c}{x}_{2}^{1}\\ {x}_{2}^{3}\\ {x}_{2}^{4}\end{array}\right|,$$
(A.3)
$${\alpha }_{3}=\left|\begin{array}{c}{x}_{1}^{1}\\ {x}_{1}^{2}\\ {x}_{1}^{4}\end{array} \begin{array}{c}{x}_{2}^{1}\\ {x}_{2}^{2}\\ {x}_{2}^{4}\end{array} \begin{array}{c}{x}_{3}^{1}\\ {x}_{3}^{2}\\ {x}_{3}^{4}\end{array}\right|, {\beta }_{3}=-\left|\begin{array}{c}1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{2}^{1}\\ {x}_{2}^{2}\\ {x}_{2}^{4}\end{array} \begin{array}{c}{x}_{3}^{1}\\ {x}_{3}^{2}\\ {x}_{3}^{4}\end{array}\right|, {\gamma }_{3}=\left|\begin{array}{c}1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{1}^{1}\\ {x}_{1}^{2}\\ {x}_{1}^{4}\end{array} \begin{array}{c}{x}_{3}^{1}\\ {x}_{3}^{2}\\ {x}_{3}^{4}\end{array}\right|, {\delta }_{3}=-\left|\begin{array}{c}1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{1}^{1}\\ {x}_{1}^{2}\\ {x}_{1}^{4}\end{array} \begin{array}{c}{x}_{2}^{1}\\ {x}_{2}^{2}\\ {x}_{2}^{4}\end{array}\right|,$$
(A.4)
$${\alpha }_{4}=-\left|\begin{array}{c}{x}_{1}^{1}\\ {x}_{1}^{2}\\ {x}_{1}^{3}\end{array} \begin{array}{c}{x}_{2}^{1}\\ {x}_{2}^{2}\\ {x}_{2}^{3}\end{array} \begin{array}{c}{x}_{3}^{1}\\ {x}_{3}^{2}\\ {x}_{3}^{3}\end{array}\right|, {\beta }_{3}=\left|\begin{array}{c}1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{2}^{1}\\ {x}_{2}^{2}\\ {x}_{2}^{3}\end{array} \begin{array}{c}{x}_{3}^{1}\\ {x}_{3}^{2}\\ {x}_{3}^{3}\end{array}\right|, {\gamma }_{3}=-\left|\begin{array}{c}1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{1}^{1}\\ {x}_{1}^{2}\\ {x}_{1}^{3}\end{array} \begin{array}{c}{x}_{3}^{1}\\ {x}_{3}^{2}\\ {x}_{3}^{3}\end{array}\right|, {\delta }_{3}=\left|\begin{array}{c}1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{1}^{1}\\ {x}_{1}^{2}\\ {x}_{1}^{3}\end{array} \begin{array}{c}{x}_{2}^{1}\\ {x}_{2}^{2}\\ {x}_{2}^{3}\end{array}\right|,$$
(A.5)
$$6V=\left|\begin{array}{c}1\\ 1\\ 1\\ 1\end{array} \begin{array}{c}{x}_{1}^{1}\\ {x}_{1}^{2}\\ {x}_{1}^{3}\\ {x}_{1}^{4}\end{array} \begin{array}{c}{x}_{2}^{1}\\ {x}_{2}^{2}\\ {x}_{2}^{3}\\ {x}_{2}^{4}\end{array} \begin{array}{c}{x}_{3}^{1}\\ {x}_{3}^{2}\\ {x}_{3}^{3}\\ {x}_{3}^{4}\end{array}\right|,$$
(A.6)

where the superscript (i.e., 1, 2, 3, and 4) represents the node number and the subscript (i.e., 1, 2, and 3) represents the direction.

The elemental strain displacement matrix is

$${\left[B\right]}_{e}=\frac{1}{6V}\left[\begin{array}{c}{\beta }_{1}\\ 0\\ 0\\ 0\\ {\delta }_{1}\\ {\gamma }_{1}\end{array} \begin{array}{c}0\\ {\gamma }_{1}\\ 0\\ {\delta }_{1}\\ 0\\ {\beta }_{1}\end{array} \begin{array}{c}0\\ 0\\ {\delta }_{1}\\ {\gamma }_{1}\\ {\beta }_{1}\\ 0\end{array} \begin{array}{c}{\beta }_{2}\\ 0\\ 0\\ 0\\ {\delta }_{2}\\ {\gamma }_{2}\end{array} \begin{array}{c}0\\ {\gamma }_{2}\\ 0\\ {\delta }_{2}\\ 0\\ {\beta }_{2}\end{array} \begin{array}{c}0\\ 0\\ {\delta }_{2}\\ {\gamma }_{2}\\ {\beta }_{2}\\ 0\end{array} \begin{array}{c}{\beta }_{3}\\ 0\\ 0\\ 0\\ {\delta }_{3}\\ {\gamma }_{3}\end{array} \begin{array}{c}0\\ {\gamma }_{3}\\ 0\\ {\delta }_{3}\\ 0\\ {\beta }_{3}\end{array} \begin{array}{c}0\\ 0\\ {\delta }_{3}\\ {\gamma }_{3}\\ {\beta }_{3}\\ 0\end{array} \begin{array}{c}{\beta }_{4}\\ 0\\ 0\\ 0\\ {\delta }_{4}\\ {\gamma }_{4}\end{array} \begin{array}{c}0\\ {\gamma }_{4}\\ 0\\ {\delta }_{4}\\ 0\\ {\beta }_{4}\end{array} \begin{array}{c}0\\ 0\\ {\delta }_{4}\\ {\gamma }_{4}\\ {\beta }_{4}\\ 0\end{array}\right].$$
(A.7)

The elemental electric field and electric potential matrix is

$${\left[{B}_{\phi }\right]}_{e}=\left[\begin{array}{c}\frac{\partial {N}_{1}}{\partial {x}_{1}}\\ \frac{\partial {N}_{1}}{\partial {x}_{2}}\\ \frac{\partial {N}_{1}}{\partial {x}_{3}}\end{array} \begin{array}{c}\frac{\partial {N}_{2}}{\partial {x}_{1}}\\ \frac{\partial {N}_{2}}{\partial {x}_{2}}\\ \frac{\partial {N}_{2}}{\partial {x}_{3}}\end{array} \begin{array}{c}\frac{\partial {N}_{3}}{\partial {x}_{1}}\\ \frac{\partial {N}_{3}}{\partial {x}_{2}}\\ \frac{\partial {N}_{3}}{\partial {x}_{3}}\end{array} \begin{array}{c}\frac{\partial {N}_{4}}{\partial {x}_{1}}\\ \frac{\partial {N}_{4}}{\partial {x}_{2}}\\ \frac{\partial {N}_{4}}{\partial {x}_{3}}\end{array}\right].$$
(A.8)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Singh, D., Sharma, S., Kumar, R. et al. Representative volume element model of triply periodic minimal surfaces (TPMS)-based electrostrictive composites for numerical evaluation of effective properties. Acta Mech 234, 355–375 (2023). https://doi.org/10.1007/s00707-022-03404-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-022-03404-2

Search

Navigation