Skip to main content

Advertisement

SpringerLink
Log in

Investigation of the static behavior of a micropolar functionally graded plate using two finite element methods in Hilbert space and differential transformation method

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

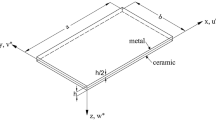
The main purpose of this paper is to analyze the bending of a micropolar functional graded plate depending on the splitting parameter, with two finite element methods in Hilbert space and the semi-analytical method of differential transformations, the advantages and disadvantages of using these two methods. The problem is developed using enhanced mathematical methods and kinematic assumption that the forces are defined based on the existing boundary conditions and using the internal energy of the plate, which are extracted by a splitting parameter. The splitting parameter is the optimal value for the minimization of the elastic energy which increases the degree of freedom and controls the force applied to the plate. The variation of the separator operating parameters is investigated by changing the degree of functionally graded material. Finally, the effects of the changes in the behavior of the plate are examined by changing the degree of functionally graded materials, which is defined along with the thickness of the plates. The influence of plate length and thickness, as well as the degree of FG material, are investigated on the kinematic variables of a clamped plate. Furthermore, the superiority of the various solution methods is examined. Because the two methods converge, the DTM method provided more efficient results in terms of processing time and expenditure as well as using the analytical equation to obtain precise solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Abbreviations

E :

Elasticity modulus

Z :

Thickness coordinate

h :

Thickness of the plate

\(P_{p}\) :

Material properties of polyurethane foam

\(P_{s}\) :

Material properties of synthetic foam

\(\sigma _{ij}\) :

Cauchy stress tensor

\(\mu _{ij}\) :

Couple-stress tensor

\(\varepsilon _{ijk}\) :

Levi-Civita tensor

\(\rho \) :

Density

f :

Force on the plate

\(u_{i}\) :

Displacement vector

\(l_{i}\) :

Body coupling

j :

Microinertia

\(\phi \) :

Microrotation vector

\(\gamma _{ij}\) :

Micropolar strain tensor

\(\chi _{ij}\) :

Micropolar torsion-rotation tensor

\(\alpha ,\beta ,\gamma ,\varepsilon \) :

The asymmetric elasticity constants

\(\lambda ,\mu \) :

Lamé parameters

G :

The boundary of the middle surface

\(\psi _{1},\psi _{2}\) :

The rotation of the middle plate

\(W+W^{*}\) :

Vertical deflection

\(\frac{5}{4}\Omega _{\alpha }^{0}+{\hat{\Omega }}_{\alpha }\) :

Indicates microrotation

\(\Omega _{3}\) :

Rate of change of the microrotation

\(\sigma ^{t}\) :

Cauchy stress at the top of the plate

\(\mu ^{t}\) :

Couple stress at the top of the plate

\(\sigma ^{b}\) :

Cauchy stress at the bottom of the plate

\(\mu ^{b}\) :

Couple stress at the bottom of the plate

p :

Bending pressure

\(\eta \) :

Splitting parameter

\(p_{1},p_{1}\) :

Bending pressure is divided by \(\eta \)

\(\Theta \) :

HPR function

\({\mathcal {U}}\) :

Set of kinematic variables

S :

Set of micropolar plate stress

\(M_{11},M_{22}\) :

Bending moments

\(M_{12},M_{21}\) :

Twisting moments

\(Q_{\alpha }\) :

Shear force

\(Q_{\alpha }^{*},{\hat{Q}}_{\alpha }\) :

Transverse shear force

\(R_{11},R_{22},R_{11}^{*},R_{22}^{*}\) :

Micropolar bending moments

\(R_{12},R_{21},R_{12}^{*},R_{21}^{*}\) :

Micropolar twisting moments

\(S_{\alpha }^{*}\) :

Micropolar couple moments

\({\mathcal {E}}\) :

The set of micropolar plate strain

L :

Operator matrix

\({\mathcal {F}}\) :

Force vector

\({\mathcal {W}}^{\eta }\) :

Density of the work

\(H^{1}(B_{0})\) :

The standard function in Hilbert space

\(\nu \) :

Poisson’s ratio

\(l_{b}\) :

Characteristic length of twisting

\(l_{t}\) :

Characteristic length of twisting

N :

The couplings number

References

  1. Daikh, A.A., Zenkour, A.M.: Free vibration and buckling of porous power-law and sigmoid functionally graded sandwich plates using a simple higher-order shear deformation theory. Mater. Res. Exp. 6(11), 115707 (2019). https://doi.org/10.1088/2053-1591/ab48a9

    Article  Google Scholar 

  2. Eltaher, M., Alshorbagy, A., Mahmoud, F.: Determination of neutral axis position and its effect on natural frequencies of functionally graded macro/nanobeams. Compos. Struct. 99, 193–201 (2013). https://doi.org/10.1016/j.compstruct.2012.11.039

    Article  Google Scholar 

  3. Birman, V., Byrd, L.W.: Modeling and analysis of functionally graded materials and structures. Appl. Mech. Rev. 60(5), 195–216 (2007) https://doi.org/10.1115/1.2777164, https://asmedigitalcollection.asme.org/appliedmechanicsreviews/article-pdf/60/5/195/5441833/195_1.pdf

  4. Vel, S.S., Batra, R.: Three-dimensional exact solution for the vibration of functionally graded rectangular plates. J. Sound Vib. 272(3), 703–730 (2004). https://doi.org/10.1016/S0022-460X(03)00412-7

    Article  Google Scholar 

  5. Uymaz, B., Aydogdu, M.: Three-dimensional vibration analyses of functionally graded plates under various boundary conditions. J. Reinf. Plastics Compos. 26(18), 1847–1863 (2007). https://doi.org/10.1177/0731684407081351

    Article  Google Scholar 

  6. Jin, G., Su, Z., Shi, S., Ye, T., Gao, S.: Three-dimensional exact solution for the free vibration of arbitrarily thick functionally graded rectangular plates with general boundary conditions. Compos. Struct. 108, 565–577 (2014). https://doi.org/10.1016/j.compstruct.2013.09.051

    Article  Google Scholar 

  7. Reddy, J.N., Cheng, Z.-Q.: Frequency of functionally graded plates with three-dimensional asymptotic approach. J. Eng. Mech. 129(8), 896–900 (2003). https://doi.org/10.1061/(ASCE)0733-9399(2003)129:8(896)

    Article  Google Scholar 

  8. Malikan, M., Eremeyev, V.A.: A new hyperbolic-polynomial higher-order elasticity theory for mechanics of thick fgm beams with imperfection in the material composition. Compos. Struct. 249, 112486 (2020). https://doi.org/10.1016/j.compstruct.2020.112486

    Article  Google Scholar 

  9. Malikan, M., Wiczenbach, T., Eremeyev, V.A.: Thermal buckling of functionally graded piezomagnetic micro-and nanobeams presenting the flexomagnetic effect. Continuum Mech. Thermodyn. 1–16 (2021)

  10. Dastjerdi, S., Malikan, M., Eremeyev, V.A., Akgöz, B., Civalek, Ö.: On the generalized model of shell structures with functional cross-sections. Compos. Struct. 272, 114192 (2021). https://doi.org/10.1016/j.compstruct.2021.114192

  11. Dastjerdi, S., Malikan, M., Dimitri, R., Tornabene, F.: Nonlocal elasticity analysis of moderately thick porous functionally graded plates in a hygro-thermal environment. Compos. Struct. 255, 112925 (2021). https://doi.org/10.1016/j.compstruct.2020.112925

    Article  Google Scholar 

  12. Dastjerdi, S., Akgöz, B.: New static and dynamic analyses of macro and nano fgm plates using exact three-dimensional elasticity in thermal environment. Compos. Struct. 192, 626–641 (2018). https://doi.org/10.1016/j.compstruct.2018.03.058

    Article  Google Scholar 

  13. Dastjerdi, S., Akgöz, B., Civalek, Ö.: On the effect of viscoelasticity on behavior of gyroscopes. Int. J. Eng. Sci. 149, 103236 (2020). https://doi.org/10.1016/j.ijengsci.2020.103236

  14. Eringen, A.C.: On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 54(9), 4703–4710 (1983)

    Article  Google Scholar 

  15. Mindlin, R.: Influence of Couple-stresses on Stress Concentrations. COLUMBIA UNIV NEW YORK, Technical Report (1962)

  16. Mindlin, R.: Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1(4), 417–438 (1965). https://doi.org/10.1016/0020-7683(65)90006-5

    Article  Google Scholar 

  17. Gurtin, M.E., Murdoch, A.I.: A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 57(4), 291–323 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  18. Shaat, M., Abdelkefi, A.: New insights on the applicability of Eringen’s nonlocal theory. Int. J. Mech. Sci. 121, 67–75 (2017). https://doi.org/10.1016/j.ijmecsci.2016.12.013

    Article  Google Scholar 

  19. Eringen, A.C.: Theory of micropolar plates. Z. Angew. Math. Phys. ZAMP 18(1), 12–30 (1967)

    Article  Google Scholar 

  20. Gurtin, M.E.: The linear theory of elasticity, pp. 1–295. Springer, Berlin (1973)

    Book  Google Scholar 

  21. Merkel, A., Tournat, V., Gusev, V.: Experimental evidence of rotational elastic waves in granular phononic crystals. Phys. Rev. Lett. 107(22), 225502 (2011)

    Article  Google Scholar 

  22. Altenbach, H., Eremeyev, V.A.: in Thin-walled Structures Made of Foams, pp 167–242 Springer (2010)

  23. Gerstle, W., Sau, N., Aguilera, E.: Micropolar peridynamic constitutive model for concrete (2007)

  24. Chang, T.-P., Lin, H.-C., Chang, W.-T., Hsiao, J.-F.: Engineering properties of lightweight aggregate concrete assessed by stress wave propagation methods. Cement Concr. Compos. 28(1), 57–68 (2006). https://doi.org/10.1016/j.cemconcomp.2005.08.003

    Article  Google Scholar 

  25. Kumar, R.: Wave propagation in micropolar viscoelastic generalized thermoelastic solid. Int. J. Eng. Sci. 38(12), 1377–1395 (2000). https://doi.org/10.1016/S0020-7225(99)00057-9

    Article  Google Scholar 

  26. Anderson, W., Lakes, R.: Size effects due to Cosserat elasticity and surface damage in closed-cell polymethacrylimide foam. J. Mater. Sci. 29(24), 6413–6419 (1994)

    Article  Google Scholar 

  27. Lakes, R.: Experimental microelasticity of two porous solids. Int. J. Solids Struct. 22(1), 55–63 (1986). https://doi.org/10.1016/0020-7683(86)90103-4

    Article  Google Scholar 

  28. Gauthier, R.D., Jahsman, W.E.: A quest for micropolar elastic constants. J. Appl. Mech. 42(2), 369–374 (1975). https://doi.org/10.1115/1.3423583

    Article  MATH  Google Scholar 

  29. Eringen, A.: Microcontinuum Field Theories i: Foundations and Solids Springer-verlag. New York, Berlin, Heidelberg (1999)

    Book  MATH  Google Scholar 

  30. Cosserat, E., Cosserat, F.: Theorie des corps dédormables A. Hermann et fils, (1906)

  31. Reissner, E.: Reflections on the theory of elastic plates. Appl. Mech. Rev. 38(11), 1453–1464 (1985). https://doi.org/10.1115/1.3143699

    Article  Google Scholar 

  32. Rössle, A., Bischoff, M., Wendland, W., Ramm, E.: On the mathematical foundation of the (1,1,2)-platemodel. Int. J. Solids Struct. 36(14), 2143–2168 (1999). https://doi.org/10.1016/S0020-7683(98)00071-7

    Article  MATH  Google Scholar 

  33. Steinberg, L.: Deformation of micropolar plates of moderate thickness. Int. J. Appl. Math. Mech. 6(17), 1–24 (2010)

    Google Scholar 

  34. Bauer, S., Schäfer, M., Grammenoudis, P., Tsakmakis, C.: Three-dimensional finite elements for large deformation micropolar elasticity. Comp. Meth. Appl. Mech. Eng. 199(41), 2643–2654 (2010). https://doi.org/10.1016/j.cma.2010.05.002

    Article  MathSciNet  MATH  Google Scholar 

  35. Sargsyan, S.H.: in Mathematical Models of Micropolar Elastic Thin Shells 91–100 Springer, (2011)

  36. Sargsyan, S., Sargsyan, A.: General dynamic theory of micropolar elastic thin plates with free rotation and special features of their natural oscillations. Acoust. Phys. 57(4), 473–481 (2011)

    Article  Google Scholar 

  37. Steinberg, L., Kvasov, R.: Enhanced mathematical model for Cosserat plate bending. Thin-Walled Struct. 63, 51–62 (2013). https://doi.org/10.1016/j.tws.2012.10.003

    Article  Google Scholar 

  38. Kvasov, R., Steinberg, L.: Numerical modeling of bending of micropolar plates. Thin-Walled Struct. 69, 67–78 (2013). https://doi.org/10.1016/j.tws.2013.04.001

    Article  Google Scholar 

  39. Sargsyan, A., Sargsyan, S.: Dynamic model of micropolar elastic thin plates with independent fields of displacements and rotations. J. Sound Vib. 333(18), 4354–4375 (2014). https://doi.org/10.1016/j.jsv.2014.04.048

    Article  Google Scholar 

  40. Abadikhah, H., Folkow, P.D.: A hierarchy of dynamic equations for micropolar plates. J. Sound Vib. 357, 427–436 (2015). https://doi.org/10.1016/j.jsv.2015.08.005

    Article  Google Scholar 

  41. Abadikhah, H., Folkow, P.D.: A rational derivation of dynamic higher order equations for functionally graded micropolar plates. Compos. Struct. 153, 234–241 (2016). https://doi.org/10.1016/j.compstruct.2016.05.090

    Article  Google Scholar 

  42. Ansari, R., Shakouri, A.H., Bazdid-Vahdati, M., Norouzzadeh, A., Rouhi, H.: A Nonclassical finite element approach for the nonlinear analysis of micropolar plates. J. Comput. Nonlinear Dyn. 12(1) (2016). https://doi.org/10.1115/1.4034678,011019, https://asmedigitalcollection.asme.org/computationalnonlinear/article-pdf/12/1/011019/6108352/cnd_012_01_011019.pdf

  43. Zozulya, V.: Higher order theory of micropolar plates and shells. ZAMM - J. Appl. Math. Mech./Z. für Angewandte Math. Mech. 98(6), 886–918 (2018). https://doi.org/10.1002/zamm.201700317

    Article  MathSciNet  Google Scholar 

  44. Shaw, S.: Bending of a thin rectangular isotropic micropolar plate. Int. J. Comput. Meth. Eng. Sci. Mech. 20(1), 64–71 (2019). https://doi.org/10.1080/15502287.2019.1568616

    Article  MathSciNet  Google Scholar 

  45. Carrera, E., Zozulya, V.V.: Carrera unified formulation (cuf) for the micropolar plates and shells. i. Higher order theory. Mech. Adv. Mater. Struct. 0(0), 1–23 (2020). https://doi.org/10.1080/15376494.2020.1793241

  46. Carrera, E., Zozulya, V.V.: Carrera unified formulation (cuf) for the micropolar plates and shells. ii. Complete linear expansion case. Mech. Adv. Mater. Struct. 0(0), 1–20 (2020). https://doi.org/10.1080/15376494.2020.1793242

  47. Zozulya, V.V., Carrera, E.: Carrera unified formulation (cuf) for the micropolar plates and shells. iii. Classical models. Mech. Adv. Mater. Struct. 0(0), 1–21 (2021). https://doi.org/10.1080/15376494.2021.1975855

  48. Pompe, W., et al.: Functionally graded materials for biomedical applications. Mater. Sci. Eng. A 362(1), 40–60 (2003). https://doi.org/10.1016/S0921-5093(03)00580-X

    Article  Google Scholar 

  49. Miao, X., Sun, D.: Graded/gradient porous biomaterials. Materials 3(1), 26–47 (2009)

    Article  Google Scholar 

  50. Petit, C., Montanaro, L., Palmero, P.: Functionally graded ceramics for biomedical application: Concept, manufacturing, and properties. Int. J. Appl. Ceramic Technol. 15(4), 820–840 (2018)

    Article  Google Scholar 

  51. Gupta, B.: Few studies on biomedical applications of functionally graded material. Int. J. Eng. Technol. Sci. Res. IJETSR 4, 39–43 (2017)

    Google Scholar 

  52. Sajjad, A., Bakar, W.Z., Basri, S., Jamaludin, S.N.: Functionally graded materials: an overview of dental applications. World J. Dentist. 9(2), 137–144 (2018)

    Article  Google Scholar 

  53. Tharaknath, S., Ramkumar, R., Lokesh, B.: Design and analysis of hip prosthesis using functionally graded material. Middle East J. Sci. Res. 24, 124–132 (2016)

    Google Scholar 

  54. Almasi, D., Sadeghi, M., Lau, W.J., Roozbahani, F., Iqbal, N.: Functionally graded polymeric materials: A brief review of current fabrication methods and introduction of a novel fabrication method. Mater. Sci. Eng. C 64, 102–107 (2016). https://doi.org/10.1016/j.msec.2016.03.053

    Article  Google Scholar 

  55. Yuan, Y., Zhao, K., Sahmani, S., Safaei, B.: Size-dependent shear buckling response of fgm skew nanoplates modeled via different homogenization schemes. Appl. Math. Mech. 41(4) (2020)

  56. Bouafia, H., et al.: Natural frequencies of fgm nanoplates embedded in an elastic medium. Adv. Nano Res. 11(3), 239–249 (2021)

    Google Scholar 

  57. Dastjerdi, S., Akgöz, B.: New static and dynamic analyses of macro and nano fgm plates using exact three-dimensional elasticity in thermal environment. Compos. Struct. 192, 626–641 (2018). https://doi.org/10.1016/j.compstruct.2018.03.058

    Article  Google Scholar 

  58. Chen, S.-X., Sahmani, S., Safaei, B.: Size-dependent nonlinear bending behavior of porous fgm quasi-3d microplates with a central cutout based on nonlocal strain gradient isogeometric finite element modelling. Eng. Comput. 37(2), 1657–1678 (2021)

    Article  Google Scholar 

  59. Lakes, R.: Experimental methods for study of Cosserat elastic solids and other generalized elastic continua. Cont. Models Mater. Microstruct. 70, 1–25 (1995)

    MATH  Google Scholar 

  60. Zhou, J.: Differential Transformation and its Applications for Electrical Circuits (1986)

  61. Chen, C.-K., Ho, S.-H.: Application of differential transformation to eigenvalue problems. Appl. Math. Comput. 79(2), 173–188 (1996). https://doi.org/10.1016/0096-3003(95)00253-7

    Article  MathSciNet  MATH  Google Scholar 

  62. Attarnejad, R., Shahba, A., Semnani, S.J.: Application of differential transform in free vibration analysis of Timoshenko beams resting on two-parameter elastic foundation. Arabian J. Sci. Eng. 35(2B), 125–132 (2010)

    Google Scholar 

  63. Kaya, M., Ozdemir Ozgumus, O.: Flexural-torsional-coupled vibration analysis of axially loaded closed-section composite Timoshenko beam by using dtm. J. Sound Vib. 306(3), 495–506 (2007). https://doi.org/10.1016/j.jsv.2007.05.049

    Article  Google Scholar 

  64. Kaya, M.O.: Free vibration analysis of a rotating Timoshenko beam by differential transform method. Aircr. Eng. Aerosp, Technol (2006)

  65. Kuang Chen, C., Huei Ho, S.: Solving partial differential equations by two-dimensional differential transform method. Appl. Math. Comput. 106(2), 171–179 (1999). https://doi.org/10.1016/S0096-3003(98)10115-7

    Article  MathSciNet  MATH  Google Scholar 

  66. Jang, M.-J., Chen, C.-L., Liu, Y.-C.: Two-dimensional differential transform for partial differential equations. Appl. Math. Comput. 121(2), 261–270 (2001). https://doi.org/10.1016/S0096-3003(99)00293-3

    Article  MathSciNet  MATH  Google Scholar 

  67. Ayaz, F.: Applications of differential transform method to differential-algebraic equations. Appl. Math. Comput. 152(3), 649–657 (2004). https://doi.org/10.1016/S0096-3003(03)00581-2

    Article  MathSciNet  MATH  Google Scholar 

  68. Ayaz, F.: On the two-dimensional differential transform method. Appl. Math. Comput. 143(2), 361–374 (2003). https://doi.org/10.1016/S0096-3003(02)00368-5

    Article  MathSciNet  MATH  Google Scholar 

  69. Chang, S.-H., Chang, I.-L.: A new algorithm for calculating two-dimensional differential transform of nonlinear functions. Appl. Math. Comput. 215(7), 2486–2494 (2009). https://doi.org/10.1016/j.amc.2009.08.046

    Article  MathSciNet  MATH  Google Scholar 

  70. Tari, A., Rahimi, M., Shahmorad, S., Talati, F.: Solving a class of two-dimensional linear and nonlinear Volterra integral equations by the differential transform method. J. Comput. Appl. Math. 228(1), 70–76 (2009). https://doi.org/10.1016/j.cam.2008.08.038

    Article  MathSciNet  MATH  Google Scholar 

  71. Jang, B.: Comments on “Solving a class of two-dimensional linear and nonlinear Volterra integral equations by the differential transform method’’. J. Comput. Appl. Math. 233(2), 224–230 (2009). https://doi.org/10.1016/j.cam.2009.07.012

    Article  MathSciNet  MATH  Google Scholar 

  72. Darania, P., Shali, J.A., Ivaz, K.: New computational method for solving some 2-dimensional nonlinear Volterra integro-differential equations. Numer. Algor. 57(1), 125–147 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  73. Chi, S.-H., Chung, Y.-L.: Mechanical behavior of functionally graded material plates under transverse load-part ii: Numerical results. Int. J. Solids Struct. 43(13), 3675–3691 (2006). https://doi.org/10.1016/j.ijsolstr.2005.04.010

    Article  MATH  Google Scholar 

  74. Reissner, E.: The effect of transverse shear deformation on the bending of elastic plates. J. Appl. Mech. 12(2), A69–A77 (1945). https://doi.org/10.1115/1.4009435

    Article  MathSciNet  MATH  Google Scholar 

  75. Fürst, D., et al.: Characterization of synthetic foam structures used to manufacture artificial vertebral trabecular bone. Mater. Sci. Eng. C 76, 1103–1111 (2017). https://doi.org/10.1016/j.msec.2017.03.158

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Urmia University of Technology, Urmia, Iran

    Ahad Ahmadpour fard, Shirko Faroughi & Leyla Abbasiniyan

  2. Department of Mathematics, Urmia University, Urmia, 165, Iran

    Parviz Darania

Authors
  1. Ahad Ahmadpour fard
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shirko Faroughi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Parviz Darania
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Leyla Abbasiniyan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shirko Faroughi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahmadpour fard, A., Faroughi, S., Darania, P. et al. Investigation of the static behavior of a micropolar functionally graded plate using two finite element methods in Hilbert space and differential transformation method. Acta Mech 233, 4441–4466 (2022). https://doi.org/10.1007/s00707-022-03325-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-022-03325-0

Search

Navigation