Skip to main content
SpringerLink
Log in

Reduced motion equations of an axisymmetric body spinning on a horizontal surface via Lie symmetries

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

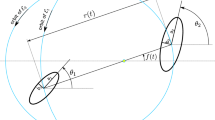
In this paper, the general analytical solution of the mechanical system consisting of an axisymmetric body spinning on a horizontal surface is analyzed. The motion equations are given by a three-dimensional system in which one of the equations is of second order. The invariance of the system under time translation is applied to reduce the order of the system by means of the classical Lie reduction method. As a result, a reduced autonomous first-order system is obtained. It is also explained how to recover the general analytical solution of the original system from the general solution of the reduced motion equations. Finally, some particular situations are considered with the goal of developing further the expression of the analytical solution found. The case of a spinning polar spheroid is also addressed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Ambrose, D.M., Kelliher, J.P., Filho, M.C.L., Lopes, H.J.N.: Serfati solutions to the 2d Euler equations on exterior domains. J. Differ. Equ. 259(9), 4509–4560 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  2. Ariska, M., Akhsan, H., Muslim, M.: Dynamic analysis of Tippe top on cylinder’s inner surface with and without friction based on Routh reduction. J. Phys. Conf. Ser. 1467, 012040 (2020)

    Article  Google Scholar 

  3. Ariska, M., Akhsan, H., Zulherman, Z.: Utilization of maple-based physics computation in determining the dynamics of Tippe top. Jurnal Penelitian Fisika dan Aplikasinya (JPFA) 8(2), 123 (2018)

    Article  Google Scholar 

  4. Bartsch, T., Ding, Y.: Periodic solutions of superlinear beam and membrane equations with perturbations from symmetry. Nonlinear Anal. Theory Methods Appl. 44(6), 727–748 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  5. Basquerotto, C.H.C.C., Righetto, E., da Silva, S.: As simetrias de Lie de um pião. Revista Brasileira de Ensino de Física, 40(2) (2017)

  6. Basquerotto, C.H.C.C., Righetto, E., da Silva, S.: Applications of the Lie symmetries to complete solution of a bead on a rotating wire hoop. J. Braz. Soc. Mech. Sci. Eng. 40(2) (2018)

  7. Basquerotto, C.H.C.C., Ruiz, A.: On the reduction of nonlinear mechanical systems via moving frames: a bead on a rotating wire hoop and a spinning top. Acta Mech. 231(12), 4867–4879 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bluman, G.: Symmetries and Differential Equations. Springer, New York (1989)

    Book  MATH  Google Scholar 

  9. Bluman, G., Anco, S.: Symmetry and Integration Methods for Differential Equations. Springer, New York (2002)

    MATH  Google Scholar 

  10. Bocko, J., Nohajová, V., Harčarik, T.: Symmetries of differential equations describing beams and plates on elastic foundations. Procedia Eng. 48, 40–45 (2012)

    Article  Google Scholar 

  11. Borisov, A.V., Ivanov, A.P.: Dynamics of the tippe top on a vibrating base. Regular Chaotic Dyn. 25(6), 707–715 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  12. Braams, C.: On the influence of friction on the motion of a top. Physica 18(8–9), 503–514 (1952)

    Article  MathSciNet  MATH  Google Scholar 

  13. Branicki, M., Moffatt, H., Shimomura, Y.: Dynamics of an axisymmetric body spinning on a horizontal surface. III. geometry of steady state structures for convex bodies. Proc. R. Soc. A Math. Phys. Eng. Sci. 462(2066), 371–390 (2005)

  14. Branicki, M., Shimomura, Y.: Dynamics of an axisymmetric body spinning on a horizontal surface. IV. stability of steady spin states and the ‘rising egg’ phenomenon for convex axisymmetric bodies. Proc. R. Soc. A Math. Phys. Eng. Sci. 462(2075), 3253–3275 (2006)

  15. Campo, A.R.D.: Tippe top (topsy-turnee top) continued. Am. J. Phys. 23(8), 544–545 (1955)

    Article  Google Scholar 

  16. Clarksonz, P.A., Mansfield, E.L.: Symmetry reductions and exact solutions of a class of nonlinear heat equations. Physica D 70(3), 250–288 (1994)

    Article  MathSciNet  Google Scholar 

  17. Cohen, R.J.: The tippe top revisited. Am. J. Phys. 45(1), 12–17 (1977)

    Article  Google Scholar 

  18. Craddock, M.: Symmetry groups of linear partial differential equations and representation theory: The Laplace and axially symmetric wave equations. J. Differ. Equ. 166(1), 107–131 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  19. Ebenfeld, S., Scheck, F.: A new analysis of the Tippe top: Asymptotic states and Liapunov stability. Ann. Phys. 243(2), 195–217 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  20. Fang, Y., Fu, W., An, C., Yuan, Z., Fei, J.: Modelling, simulation and dynamic sliding mode control of a MEMS gyroscope. Micromachines 12(2), 190 (2021)

    Article  Google Scholar 

  21. Featherstone, R.: Rigid Body Dynamics Algorithms. Springer, Berlin (2014)

    MATH  Google Scholar 

  22. Fokker, A.: The tracks of tops pegs on the floor. Physica 18(8–9), 497–502 (1952)

    Article  MATH  Google Scholar 

  23. Friswell, M.I., Penny, J.E.T., Garvey, S.D.: Dynamics of Rotating Machines. Cambridge University Press, Cambridge (2010)

    Book  MATH  Google Scholar 

  24. Genta, G.: Dynamics of Rotating Systems. Springer, Berlin (2007)

    Google Scholar 

  25. Goldstein, H.: Classical Mechanics. Addison Wesley, San Francisco (2002)

    MATH  Google Scholar 

  26. Gray, C.G., Nickel, B.G.: Constants of the motion for nonslipping tippe tops and other tops with round pegs. Am. J. Phys. 68(9), 821–828 (2000)

    Article  Google Scholar 

  27. Hydon, P.E.: Symmetry Methods for Differential Equations. Cambridge University Press, Cambridge (2005)

    MATH  Google Scholar 

  28. Ibragimov, N.H.: A Practical Course in Differential Equations and Mathematical Modelling: Classical and New Methods, Nonlinear Mathematical Models. Symmetry and Invari, World Scientific Pub Co Inc (2010)

  29. Lane, M.T.: On analytic modeling of lunar perturbations of artificial satellites of the earth. Celest. Mech. Dyn. Astron. 46(4), 287–305 (1989)

    Article  MATH  Google Scholar 

  30. Li, Q., Xiao, D., Zhou, X., Hou, Z., Zhuo, M., Xu, Y., Wu, X.: Dynamic modeling of the multiring disk resonator gyroscope. Micromachines 10(3), 181 (2019)

    Article  Google Scholar 

  31. Liu, C.S.: Elastoplastic models and oscillators solved by a Lie-group differential algebraic equations method. Int. J. Nonlinear Mech. 69, 93–108 (2015)

  32. Luo, S., Hu, W., Yu, J., Zhu, R., He, L., Li, X., Ma, P., Wang, C., Liu, F., Roeterdink, W.G., Stolte, S., Ding, D.: Rotational dynamics of quantum state-selected symmetric-top molecules in nonresonant femtosecond laser fields. J. Phys. Chem. A 121(4), 777–783 (2017)

    Article  Google Scholar 

  33. Mankala, K.K., Agrawal, S.K.: Dynamic modeling and simulation of satellite tethered systems. J. Vib. Acoust. 127(2), 144–156 (2004)

    Article  Google Scholar 

  34. Moffatt, H.K., Shimomura, Y.: Spinning eggs: a paradox resolved. Nature 416(6879), 385–386 (2002)

    Article  Google Scholar 

  35. Moffatt, H.K., Shimomura, Y., Branicki, M.: Dynamics of an axisymmetric body spinning on a horizontal surface. I. Stability and the gyroscopic approximation. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 460(2052), 3643–3672 (2004)

  36. Montenbruck, O., Gill, E., Lutze, F.: Satellite orbits: models, methods, and applications. Appl. Mech. Rev. 55(2), B27 (2002)

    Article  Google Scholar 

  37. Mustafa, M., Al-Dweik, A.Y.: Noether symmetries and conservation laws of wave equation on static spherically symmetric spacetimes with higher symmetries. Commun. Nonlinear Sci. Numer. Simul. 23(1–3), 141–152 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  38. Olver, P.: Applications of Lie Groups to Differential Equations. Springer, New York (1986)

    Book  MATH  Google Scholar 

  39. Olver, P.: Equivalence, Invariants and Symmetry. Cambridge University Press, Cambridge (2008)

    MATH  Google Scholar 

  40. Paliathanasis, A., Tsamparlis, M.: Lie point symmetries of a general class of PDEs: the heat equation. J. Geom. Phys. 62(12), 2443–2456 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  41. Perry, J.: Spinning Tops and Gyroscopic Motions. Dover Publications, New York (1957)

    Google Scholar 

  42. Ruiz, A., Muriel, C., Ramírez, J.: Exact general solution and first integrals of a remarkable static Euler–Bernoulli beam equation. Commun. Nonlinear Sci. Numer. Simul. 69, 261–269 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  43. Sasaki, K.: Spinning eggs—Which end will rise? Am. J. Phys. 72(6), 775–781 (2004)

    Article  Google Scholar 

  44. Shimomura, Y., Branicki, M., Moffatt, H.: Dynamics of an axisymmetric body spinning on a horizontal surface. II. Self-induced jumping. Proc. R. Soc. A Math. Phys. Eng. Sci. 461(2058), 1753–1774 (2005)

  45. Stepanova, I.V.: Symmetry analysis of nonlinear heat and mass transfer equations under Soret effect. Commun. Nonlinear Sci. Numer. Simul. 20(3), 684–691 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  46. Thomson, W.T.: Introduction to Space Dynamics. Guilford Publications, New York (2012)

    Google Scholar 

  47. Trentin, J.F.S., Cenale, T.P., da Silva, S., de Souza Ribeiro, J.M.: Attitude control of inverted pendulums using reaction wheels: comparison between using one and two actuators. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 234(3), 420–429 (2019)

  48. Trentin, J.F.S., da Silva, S., de S. Ribeiro, J.M., Schaub, H.: An experimental study to swing up and control a pendulum with two reaction wheels. Meccanica (2021)

  49. Trentin, J.F.S., Silva, S.D., Ribeiro, J.M.D.S., Schaub, H.: Inverted pendulum nonlinear controllers using two reaction wheels: design and implementation. IEEE Access 8, 74922–74932 (2020)

    Article  Google Scholar 

  50. Vaidya, K.S., Parker, R.G.: Space-fixed formulation for the vibration of rotating, prestressed, axisymmetric bodies and shells. J. Sound Vib. 495, 115907 (2021)

    Article  Google Scholar 

  51. Wang, C.C., Yau, H.T.: Nonlinear dynamic analysis and sliding mode control for a gyroscope system. Nonlinear Dyn. 66(1–2), 53–65 (2010)

    MathSciNet  Google Scholar 

  52. Wittenburg, J.: Dynamics of Systems of Rigid Bodies. Vieweg+Teubner Verlag, Wiesbaden (1977)

    Book  MATH  Google Scholar 

  53. Zub, S.I., Zub, S.S., Lyashko, V.S., Lyashko, N.I., Lyashko, S.I.: Mathematical model of interaction of a symmetric top with an axially symmetric external field. Cybern. Syst. Anal. 53(3), 333–345 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  54. Zub, S.S.: Hamiltonian dynamics of the symmetric top in external axially-symmetric fields. magnetic retention of a rigid body. J. Autom. Inf. Sci. 50(7), 48–69 (2018)

Download references

Acknowledgements

A. Ruiz thanks the financial support from FEDER–Ministerio de Ciencia, Innovación y Universidades–Agencia Estatal de Investigación, via the project PGC2018-101514-B-I00 and from Junta de Andalucía to the research group FQM–377. C.H.C.C. Basquerotto is grateful for the financial support provided by the Brazilian National Council for Scientific and Technological Development (CNPq - Brazil) in grant number 426050/2018-5.

Author information

Authors and Affiliations

  1. Departamento de Matemáticas, Universidad de Cádiz - UCA, 11510, Puerto Real, Spain

    Adrián Ruiz

  2. Instituto de Geociências e Engenharias, Faculdade de Engenharia Mecânica, Universidade Federal do Sul e Sudeste do Pará, Marabá, Pará, 68505-080, Brazil

    Cláudio H. C. Costa Basquerotto

Authors
  1. Adrián Ruiz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Cláudio H. C. Costa Basquerotto
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Cláudio H. C. Costa Basquerotto.

Ethics declarations

Conflict of interests

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ruiz, A., Basquerotto, C.H.C.C. Reduced motion equations of an axisymmetric body spinning on a horizontal surface via Lie symmetries. Acta Mech 233, 3853–3865 (2022). https://doi.org/10.1007/s00707-022-03306-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-022-03306-3

Search

Navigation