Skip to main content
SpringerLink
Log in

An illustrative application of the Lie symmetries in the context of first-order mechanical systems: Hathaway’s circular pursuit problem

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

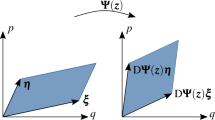
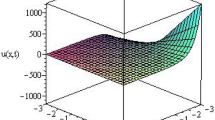
Abstract

This work illustrates how one could apply Lie point symmetries for finding the analytical solution to first-order mechanical systems. Although the classical Lie method constitutes a powerful tool for solving differential equations, an obstacle appears in the case of systems of first-order equations because they admit an infinite number of symmetries, and it is not possible to compute them by following a systematic procedure. To overcome this difficulty, we follow the idea exposed in Nucci (J. Math. Phys. 37: 1772–1775, 1996), Nucci (Electr. J. Diff. Eqn. 12: 87–101, 2005), Nucci (J. Math. Phys. 42: 746, 2001) consisting of transforming the original system to an equivalent system in which one of the equations is of second–order. The presented approach is applied to Hathaway’s circular pursuit problem, leading to the analytical solution of the system expressed in terms of the general solution to an Abel equation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Allen, L.: Evolution of flight simulation. In: Flight Simulation and Technologies, pp. 1–1. American Institute of Aeronautics and Astronautics (1993)

  2. Anco, S., Bluman, G.: Symmetry and Integration Methods for Differential Equations. Springer, New York (2002)

    MATH  Google Scholar 

  3. Barton, J.C., Eliezer, C.J.: On pursuit curves. J. Austr. Math. Soc. Ser. B Appl. Math. 41(3), 358–371 (2000)

    Article  MathSciNet  Google Scholar 

  4. Basquerotto, C.H.C.C., Righetto, E., Silva, S.D.: Applications of the Lie symmetries to complete solution of a bead on a rotating wire hoop. J. Br. Soc. Mech. Sci. Eng. 40(2), 48 (2018)

    Article  Google Scholar 

  5. Basquerotto, C.H.C.C., Ruiz, A., Righetto, E., da Silva, S.: Moving frames for Lie symmetries reduction of nonholonomic systems. Acta Mech. 230(8), 2963–2978 (2019)

    Article  MathSciNet  Google Scholar 

  6. Blumman, G.W., Kumei, S.: Symmetries and Differential Equations. Applied Mathematical Sciences, vol. 81. Springer, New York (1989)

    Book  Google Scholar 

  7. Bradley, H.C., Harding, A.M., Hathaway, A.S., Weaver, W., Corey, S.A., Gronwall, T.H., Mills, C.N., Moritz, R.E.: Problems for solution. Am. Math. Mon. 27(1), 31 (1920)

    Article  Google Scholar 

  8. Čenek, E.: Chases and escapes by Paul. J. Nahin. ACM SIGACT News 40(3), 48 (2009)

    Article  Google Scholar 

  9. Chashchina, O.I., Silagadze, Z.K.: The dog-and-rabbit chase problem as an exercise in introductory kinematics. Latin-Am. J. Phys. Educ. pp. 539–543 (2009)

  10. Davis, H.: Introduction to Nonlinear Differential and Integral Equations. Dover Publications, New York (1962)

    Google Scholar 

  11. Dichter, M.: Student Solutions Manual for Nonlinear Dynamics and Chaos, vol. 2. Westview Press, Boulder (2016)

    MATH  Google Scholar 

  12. Dopico, D., González, F., Luaces, A., Saura, M., García-Vallejo, D.: Direct sensitivity analysis of multibody systems with holonomic and nonholonomic constraints via an index-3 augmented Lagrangian formulation with projections. Nonlinear Dyn. 93(4), 2039–2056 (2018)

    Article  Google Scholar 

  13. Hoskins, J., Bluman, G.: Higher order symmetries and integrating factors for ordinary differential equations. J. Math. Anal. Appl. 435(1), 133–161 (2016)

    Article  MathSciNet  Google Scholar 

  14. Hydon, P.E.: Symmetry Methods for Differential Equations. Cambridge University Press, Cambridge (2005)

    MATH  Google Scholar 

  15. Ibragimov, N.H.: Practical Course in Differential Equations And Mathematical Modelling, A: Classical and New Methods. Nonlinear Mathematical Models Symmetry and Invariance Principles. World Scientific Publishing Co Pte Ltd, Singapore (2009)

    Book  Google Scholar 

  16. Li, J., Wu, H., Mei, F.: Dynamic analysis for the hyperchaotic system with nonholonomic constraints. Nonlinear Dyn. 90(4), 2557–2569 (2017)

    Article  MathSciNet  Google Scholar 

  17. Mungan, C.E.: A classic chase problem solved from a physics perspective. Eur. J. Phys. 26(6), 985–990 (2005)

    Article  Google Scholar 

  18. Nahin, P.J.: Chases and Escapes. Princeton University Press, New Jersey (2012)

    Book  Google Scholar 

  19. Nucci, M.C.: The complete kepler group can be derived by lie group analysis. J. Math. Phys. 37(4), 1772–1775 (1996)

    Article  MathSciNet  Google Scholar 

  20. Nucci, M.C.: Using Lie symmetries in epidemiology. Electr. J. Diff. Eqn. 12, 87–101 (2005)

    MathSciNet  MATH  Google Scholar 

  21. Nucci, M.C., Leach, P.G.L.: The harmony in the kepler and related problems. J. Math. Phys. 42(2), 746 (2001)

    Article  MathSciNet  Google Scholar 

  22. Olver, P.J.: Applications of Lie Groups to Differential Equations. Springer, New York (1986)

    Book  Google Scholar 

  23. Olver, P.J.: Equivalence, Invariants and Symmetry. Cambridge University Press, Cambridge (2008)

    MATH  Google Scholar 

  24. Rolfe, J.M., Bolton, M.: Flight simulation in the royal air force in the second world war. Aeronaut. J. 92(918), 315–327 (1988)

    Article  Google Scholar 

  25. Small, J.S.: Engineering, technology and design: the post-second world war development of electronic analogue computers. History Technol. 11(1), 33–48 (1994)

    Article  Google Scholar 

  26. Strogatz, S.: Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Studies in Nonlinearity. Westview Press, Boulder (2014)

    Google Scholar 

  27. Torrisi, V., Nucci, M.C.: Application of Lie group analysis to a mathematical model which describes HIV transmission (2001)

  28. Zaitsev, V.F., Polyanin, A.D.: Handbook of Exact Solutions for Ordinary Differential Equations. Chapman and Hall/CRC, Boca Raton (2002)

    Book  Google Scholar 

Download references

Acknowledgements

C. H. C. C. Basquerotto is grateful for the financial support provided by the Brazilian National Council for Scientific and Technological Development (CNPq - Brazil) in grant number 426050/2018-5. A. Ruiz thanks the financial support from FEDER–Ministerio de Ciencia, Innovación y Universidades–Agencia Estatal de Investigación via the project PGC2018-101514-B-I00 and from Junta de Andalucía to the research group FQM–377. S. da Silva is grateful for the financial support provided by the Brazilian National Council for Scientific and Technological Development (CNPq - Brazil) in the grant numbers 404463/2016-9 and 306526/2019-0.

Author information

Authors and Affiliations

  1. Faculdade de Engenharia Mecânica, Instituto de Geociências e Engenharias, Universidade Federal do Sul e Sudeste do Pará, Marabá, Pará, 68505-080, Brasil

    Cláudio H. C. C. Basquerotto

  2. Departamento de Matemáticas, Universidad de Cádiz - UCA, 11510, Puerto Real, Spain

    A. Ruiz

  3. Departamento de Engenharia Mecânica, Universidade Estadual Paulista - UNESP, Ilha Solteira, São Paulo, 15385-000, Brazil

    Samuel da Silva

  4. Departamento de Engenharia Mecânica, Pontifícia Universidade Católica do Rio de Janeiro - PUC-RIO, Rio de Janeiro, 22451-040, Brazil

    Hans Ingo Weber

Authors
  1. Cláudio H. C. C. Basquerotto
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Ruiz
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Samuel da Silva
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hans Ingo Weber
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Cláudio H. C. C. Basquerotto.

Ethics declarations

Conflict of interests

The authors declare that there is no conflict of interest regarding the publication of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Basquerotto, C.H.C.C., Ruiz, A., da Silva, S. et al. An illustrative application of the Lie symmetries in the context of first-order mechanical systems: Hathaway’s circular pursuit problem. Acta Mech 233, 1031–1039 (2022). https://doi.org/10.1007/s00707-022-03150-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-022-03150-5

Search

Navigation