1 Introduction

The scouring of submerged sediment layers by fluid streams is encountered in a wide range of natural and geophysical processes, such as the local scouring of river beds [1, 2], the formation of scour-holes around piles [3,4,5], the riverbank erosion [6], as well as the formation of ripples and dunes produced by marine and fluvial flows on erodible beds [7,8,9]. The natural processes involved are of fundamental relevance in geomorphology along with environmental, fluvial, and oceanographic engineering. The macroscopic characteristics of a flow are affected by its bed shape in terms of resistance, flow rate, and transport of sediments and contaminants [10], all of these being key parameters to be controlled from a technical point of view. Despite their relevance, the phenomena governing sediment scouring and bedforms are far from being completely understood due to the coupling between the dynamics of solid aggregates with multiphase flows in the presence of turbulence and geometrically complex and time-evolving interfaces. All these aspects make the numerical and theoretical tackling of the problem non-trivial due to its strongly multi-physics, multi-scale, and nonlinear nature.

Streambed morphology and scouring have been extensively studied in the last decades. Different phenomenologies have been observed and analyzed depending on the flow conditions and mechanical properties of the sediments involved: cohesive and non-cohesive sediments. Non-cohesive sediment layers are composed of solid grains that mutually interact only via contact and lubrication forces while subjected to gravity, buoyancy, and hydrodynamic stresses [11]. Under these circumstances, if the shear stress acting on the streambed overcomes a threshold value, the flow, turbulent or laminar, erodes the bed by the entrainment of solid grains that are removed from their original positions and transported downstream by the carrier fluid [12, 13]. Then, the entrained grains might be deposited onto preferential regions giving rise to complex bedforms such as dunes and ripples [9]. When the typical size of the solid particulate composing a sediment becomes lower than a certain threshold, inter-particle attractions such as van der Waals forces cannot be neglected and exert a significant equilibrating effect on bed erodibility [14]. This kind of sediment is referred to as cohesive and can be found in many natural environments such as rivers and lakes. Under these circumstances, the mechanisms regulating the erosion process and bed shape are influenced by a large number of sediment properties that strongly interact with each other [15]. In some other circumstances, erosion acts on cohesive or stony substrates, such as mudstones, that manifest a brittle mechanical behavior [16]. In these cases, the erosion is caused by hydraulic processes involving fluid stresses, fatigue mechanisms, abrasion as well as impacts of fragments with the substrate [17, 18].

On a non-cohesive, submerged sediment layer, erosion and sediment transport give rise to the establishment of coherent and regular bed patterns. The basic mechanism governing this phenomenology has been found to rely on the instability of flattened beds in presence of sinusoidal perturbations [19]. Currently, there is common agreement that such instabilities arise from the phase-lag between perturbations of the bed thickness and the shear stress acting on the bed surface as a consequence of fluid inertia [20]. Many geometrically different and organized structures have been identified and characterized based on the specific mechanisms driving bed instability and pattern wavelengths: dunes and anti-dunes [19], ripples [21], bars [22], and chevrons [23]. Different procedures have been proposed to tackle the theoretical and numerical descriptions of the processes involved. In the frame of theoretical models, linear stability analysis has been employed to predict the conditions for the onset of specific patterns on erodible beds and their related wavelengths [23,24,25,26,27]. Among the numerical methodologies, hybrid Lagrangian–Eulerian approaches based on the coupling of distinct element method (DEM) [28] with the Navier–Stokes equations by the immersed boundary method have been reported [29,30,31,32,33]. The main advantage of these methodologies relies on a fully resolved description of the fluid flow around the solid grains that enables an accurate view into the processes governing grain entrainment as well as on the effect of turbulent structures at different length scales. In this frame, different mechanisms have been found to govern the growth and wavelength of bed patterns such as dunes and ripples. In their recent work Mazzuoli et al. [31] addressed the formation of small-scale ripples on an erodible sand bed immersed in an oscillatory flow by means of direct numerical simulation. The wavelength of the ripple pattern is found to be driven by steady recirculating cells that accumulate the solid grains onto the ripple crests. A similar growth mechanism is found by Alvarez and Franklin [33] in the large eddy simulation frame. The work focuses on the temporal evolution of subaqueous barchan dunes in an incompressible channel flow. The forces acting on the solid grains are found to peak in the upstream regions of dunes providing insights into the mechanism of upstream erosion and deposition of grains onto the dune crest region [7].

The role played by the hydrodynamical mechanisms outlined above in the erosion of non-cohesive sediments is well covered by archival literature. Conversely, some differences exist in the physical processes implied in the erosion of cohesive sediments for which literature coverage is less extended. It is generally accepted that the basic erosion mechanisms in cohesive sediments are analogous to that driving the erosion of non-cohesive ones, the effects of cohesive forces on solid aggregates being determinant in regulating the erodibility of the latter [15]. Among archival works addressing this aspect in a theoretical framework, a possible approach consists of incorporating inter-particle attraction into sediment entrainment models [14, 34]. An alternative relies on the modeling of the critical shear stress for bed erosion including the effect of extensive sediment properties such as bulk density, porosity, and particle size distribution [35]. Many other experimental studies can be found, and the reader is referred to the references for additional details [15].

Unlike for non-cohesive sediments, many well-established questions remain unanswered for what concerns the fluid-driven erosion of compact cohesive sediments. Erosion occurs due to the action of fluid forces, abrasion, and even impacts, but the relative importance of the interplaying roles of these processes has not been well quantified, yet. In many cases, the materials involved present brittle bulk mechanical properties. The detachment of fragments occurs when the local stresses induced by the flow and by granular collisions overcome the ultimate stress of the material. The critical shear stress under which the sediment break up occurs, the role of turbulent fluctuations on the erosion, sediment transport processes, and bed shape need to be further analyzed.

This paper aims at investigating the scouring and formation of scouring-structures on an initially flattened bed of homogenous and soft brittle material in a turbulent channel flow by means of direct numerical simulation. The focus is on the role of turbulence in promoting the brittle fragmentation of the streambed and the characterization of the interactions among bedforms and turbulent structures. Most of the methodologies described in archival literature to numerically tackle this kind of problem are based on coupled approaches, such as DEM, or simplified models, as linear stability analysis, that are not capable to account for solid fracture induced by fluid stresses. Moreover, such numerical approaches are based on the modeling of the mechanical behavior of the solid phase rather than on the direct solution of the governing equation of solid mechanics. In this context, we aim to address the problem in an innovative framework based on the coupling of the incompressible Navier–Stokes equations with peridynamics via an immersed boundary technique. Peridynamics consists of a reformulation of continuum mechanisms, formerly developed by Silling [36], relying on non-local integral equations. In the frame of peridynamics, solid mechanics is addressed in a Lagrangian framework: a solid medium is represented as a set of Lagrangian points mutually interacting with each other via short-range potentials. The mechanics of a solid body, including deformations, is simply described by directly solving a momentum-balance, integral equation governing the dynamics of the material points. Different constitutive relations can be used to describe both linear-elastic and nonlinear mechanical behavior. The main advantage introduced by peridynamics relies on its intrinsic capability of simply and reliably manage the crack formation and branching. Indeed, in the peridynamic frame, the formation of cracks is simply represented by the deactivation of pairwise interactions among material points. In this way, when fracture mechanics is taken into consideration, peridynamics removes the numerical instabilities arising from the singularity of derivatives in partial differential equations caused by the formation and propagation of cracks. Peridynamics has been successfully employed in recent years to tackle solid continuum problems involving fluid flows, fluid–solid interaction, fracture and erosion [37,38,39]. To the best of the authors’ knowledge, the problem reported in this paper has never been addressed in a numerical framework using a coupled solid–fluid formulation that fully resolves turbulent structures and sediment fragmentation by brittle fracture. A detailed analysis of the streambed and turbulent structures of the flow is reported, highlighting the formation of scour-holes originated by turbulent fluctuations. The distribution of the bed-formations is put in relation to the presence of stationary, small-scale vortical cells that locally enhance the erosion rate of the streambed as well as large-scale turbulent stripes that promote the formation of long valleys on the solid channel bed. The authors believe that the findings reported in this paper can contribute to the improvement of the current understanding of the scouring of cohesive sediments that might be of fundamental relevance in the development of models for environmental applications.

2 Numerical method

The fluid-driven scouring of a brittle sediment layer in a turbulent channel flow is addressed in the framework of a novel approach based on peridynamics, Navier–Stokes equations, and the immersed boundary method. The employed methodology, which includes a full coupling between solid and fluid mechanics, has been recently implemented into a massively parallel numerical code [40] based on the open-source solver for incompressible flows CaNS [41]. A brief description of the method is presented in this paper for the self-consistency of the document. For additional information concerning the methodology, validation, and testing the reader is referred to Dalla Barba and Picano [40].

2.1 Peridynamics

Peridynamics is a reformulation of continuum theory based on non-local integral equations [36]. The main advantage introduced by peridynamics consists of its capability of simply managing the discontinuities arising in a solid medium when crack formation and branching is taken into consideration. Different models have been developed within peridynamics. This paper focuses on the so-called bond-based formulation [42,43,44]. A solid body, \(\mathcal {B}\), is represented as a set of material points, treated in a Lagrangian manner, that mutually interact via short-range potentials.

Fig. 1
figure 1

Left panel: two-dimensional schematic of the discretization of a solid medium based on the partitioning of the body into rectangular, discrete material particles. The panel shows the spatial range of action of the pairwise interactions (circle of radius \(\delta \)). Right panel: pairwise interaction between a couple of finite-size material particles, \(\varvec{X}_{0,h}\) and \(\varvec{X}_{0,l}\). The volume highlighted in dark-grey, \(\Delta V_{l,h}^{in}\), is the volume of \(\varvec{X}_{0,l}\) enclosed by the circle of radius \(\delta \) centered on \(\varvec{X}_{0,h}\). The schematics refer to the non-loaded, reference configuration of the body

Full size image

Short-range interactions, the so-called bonds, act over a finite spatial distance referred to as horizon, \(\delta \). Each material point interacts with a spatially limited set of other material points referred to as its family, \(\mathcal {H}_{\varvec{X}_0}\):

$$\begin{aligned} \mathcal {H}_{\varvec{X}_0}=\left\{ \varvec{X}'_0 \in \mathcal {B}, ||\varvec{X}'_{0}-\varvec{X}_0||<\delta \right\} , \end{aligned}$$
(1)

where the Lagrangian variable \({\varvec{X}_0}\) represents the spatial coordinates of an arbitrary material point in a reference, non-loaded configuration of the body \(\mathcal {B}\). The family of each material point is evaluated in the reference configuration of a body and is not altered by the deformation of the solid. This is congruent to the fact that new internal interactions between material points cannot establish as the material deforms: each family can be viewed as a Lagrangian portion of a solid body that deforms, developing a certain distribution of body-internal forces depending on the local deformation state, but which does not establish new interactions during the deformations. For a brittle and linear-elastic body with uniform and isotropic mechanical properties, the Lagrangian equations of motion that govern the temporal evolution of the coordinates of a material point read:

$$\begin{aligned} \rho _s \frac{\mathrm{d}^2\varvec{X}_h(t)}{\mathrm{d}t^2}&=\sum _{l=1}^{N_h} \left( c_0 \ \lambda _{h,l} \ s_{h,l} \ \hat{{\varvec{v}}}_{h,l} \ \alpha _{h,l} \Delta V_l \right) +\varvec{F}_h, \end{aligned}$$
(2)
$$\begin{aligned} \frac{\mathrm{d}\varvec{X}_h(t)}{\mathrm{d}t}&=\varvec{V}_h(t), \end{aligned}$$
(3)

where \(\rho _s\) is the density of the solid, \(\varvec{X}_h\) is the Lagrangian coordinate of an arbitrary material particle evaluated at the time, t, and \(\varvec{V}_h\) its Lagrangian velocity. The number of material points in the family of particle h is \(N_h\). The variable \(\varvec{X}_{0,h}\) refers to the particle coordinates in the reference configuration of the body. The term \(\varvec{F}_h\) represents the force density (per unit volume square) acting on the Lagrangian particle h due to the action of the fluid-dynamic forces and is computed according to the procedure described in Sect. 2.2. The unit vector \(\hat{{\varvec{v}}}_{h,l}\) points from the Lagrangian position \(\varvec{X}_h\) to \(\varvec{X}_l\), both evaluated at time, t. The summation is taken over the family \(\mathcal {H}_{\varvec{X}_{0,h}}\), which contains \(N_h\) material particles in addition to the central one. The variable \(\Delta V_l\) is the volume of \(\varvec{X}_l\). Finally, the parameter \(\alpha _{h,l}\), ranging from zero to one, accounts for the fact that only a fraction of the volume of \(\varvec{X}_l\) is enclosed into the circle, or sphere for three-dimensional cases, of radius \(\delta \) centered on \(\varvec{X}_h\). The parameter \(\alpha _{h,l}\) is computed in the reference configuration of the body as

$$\begin{aligned} \alpha _{h,l}=\frac{\Delta V_{l,h}^\mathrm{in}}{\Delta V_{l,h}^\mathrm{out}+\Delta V_{l,h}^\mathrm{in}}, \end{aligned}$$
(4)

where the volumes \(\Delta V_{l,h}^\mathrm{out}\) and \(\Delta V_{l,h}^\mathrm{out}\) are defined as sketched in the left panel of Fig. 1. Additional information about the computation of \(\alpha _{h,l}\) is available in references [40, 45]. The variable \(s_{h,l}\) is referred to as bond stretch,

$$\begin{aligned}&s_{h,l}=\frac{||\varvec{X}_l-\varvec{X}_h||-|| \varvec{X}_{0,l}-\varvec{X}_{0,h}||}{||\varvec{X}_{0,l} -\varvec{X}_{0,h}||}. \end{aligned}$$
(5)

In peridynamics, the formation of a crack is represented as the deactivation of a pairwise interaction via the parameter,

$$\begin{aligned} \lambda _{h,l}= {\left\{ \begin{array}{ll} 1, \ \ \ &{} s_{h,l} \le s_0 \ \ \ \forall t \ge 0,\\ 0, \ \ \ &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$
(6)

In this framework, a crack forms due to the rupture of bonds, which occurs when the bond stretch overcomes a threshold value, \(s_0\), referred to as limit bond stretch. The latter can be related to the critical fracture energy release rate of the material, \(G_0\), Young’s modulus, E, the horizon, \(\delta \), and the geometrical configuration of the problem [42, 46],

$$\begin{aligned} s_0= {\left\{ \begin{array}{ll} \sqrt{\frac{4 \pi G_0}{9 E \delta }}, \ \ \ &{} \text {in 2D plane-stress conditions,} \\ \sqrt{\frac{5 \pi G_0}{12 E \delta }}, \ \ \ &{} \text {in 2D plane-strain conditions,} \\ \sqrt{\frac{5 G_0}{6 E \delta }}, \ \ \ &{} \text {in 3D,} \end{array}\right. } \end{aligned}$$
(7)

Once a pair interaction has been deactivated it cannot be restored. If the bond stretch returns to be smaller than the limit bond stretch, the related interaction being already deactivated, the involved particles do not interact with each other. In a similar fashion, the constant \(c_0\), referred to as micro-modulus, depends on the macroscopic mechanical properties of the material [47]:

$$\begin{aligned} c_0= {\left\{ \begin{array}{ll} \frac{9 E}{\pi p \delta ^3} \ \ \ &{} \text {in 2D plane-stress conditions,} \\ \frac{48 E}{5 \pi p \delta ^3} \ \ \ &{} \text {in 2D plane-strain conditions,} \\ \frac{12 E}{\pi \delta ^4} \ \ \ &{} \text {in\ 3D,} \end{array}\right. } \end{aligned}$$
(8)

where p refers to the depth of the body along the out-of-plane direction in the two-dimensional cases.

2.2 Explicit coupling of peridynamics and Navier–Stokes equations

The incompressible formulation of the Navier–Stokes equations is used for the numerical description of the fluid phase,

$$\begin{aligned}&\displaystyle \nabla \cdot \varvec{u} = 0, \end{aligned}$$
(9)
$$\begin{aligned}&\displaystyle \rho _f \left( \frac{\partial \varvec{u}}{\partial t} + \varvec{u} \cdot \nabla \varvec{u}\right) = -\nabla p + \mu _f \nabla ^2 \varvec{u} +\rho _f {\varvec{q}}, \end{aligned}$$
(10)

where \(\varvec{u}\) is the velocity, p the hydrodynamic pressure, \(\mu _f\) the dynamic viscosity and \(\rho _f\) the density of the fluid phase. The Navier–Stokes equations are solved using a pressure-correction approach, via second-order finite difference schemes for space discretization and a third-order Runge–Kutta time marching algorithm. The same time-marching scheme is used also for the time-stepping of Eqs. (2) and (3). The Eulerian domain is discretized by a staggered and uniform Cartesian grid. The discretization of the solid medium, in its reference configuration, is based on a Cartesian and equispaced distribution of cubic particles. The cell size of the Eulerian grid, \(\Delta _f\), and the spacing of the solid Lagrangian particles, \(\Delta _s\), are set to be equal in the initial configuration of the problem. The boundary conditions are imposed on the sides of the Eulerian domain by means of ghost nodes, whereas a discrete-forcing approach is used to impose no-slip and no-penetration boundary conditions on the solid–fluid interfaces in the framework of the immersed boundary method [48]. The forcing is represented by the term, \(\varvec{q}\), in the right-hand side of Eq. (10). The time marching scheme is summarized in Algorithm 1 in a semi-discrete notation. An explicit coupling between the governing equations of peridynamics and the Navier–Stokes equations is achieved by advancing over time Eq. (10), the time step being \(\Delta t_f\). Then, the updated fluid fields are used to compute the overall stresses exerted by the fluid on the solid surfaces, as addressed below. Finally, Eqs. (2) and (3) are advanced over the same time step, \(\Delta t_s=\Delta t_f\), by means of a sub-stepping of the time marching algorithm. Additional details about the coupling method are available in reference [40].

figure a
Fig. 2
figure 2

Two-dimensional schematic of the normal probe approach adopted to compute the hydrodynamic stresses on the fluid–solid interface. The Figure shows the stencil used to interpolate the Eulerian velocity and pressure fields on the normal probe tip as well as the local frame of reference for the computation of the stresses, \((\xi ,\eta )\), defined by the tangent and normal vector to the fluid–solid interface

Full size image

The back-reaction exerted by the fluid on the solid is evaluated in the frame of the normal probe approach [49,50,51]. The overall stresses exerted by the fluid on the solid surfaces are estimated via the evaluation of the pressure gradient and viscous stresses in the proximity of the fluid–solid interface. This approach requires the unit normal to the surface to be computed a priori together with the unit tangent and bi-normal vectors defining a local, orthogonal frame of reference. An approximation of the unit normal vector can be computed at \(\varvec{X}_h\) via the following expression:

$$\begin{aligned}&{\varvec{n}}_h=\frac{\sum _{h=1}^{N_h}\lambda _{h,l}({\varvec{X}}_l-{\varvec{X}}_h)\alpha _{h,l}\Delta V_l}{\sum _{h=1}^{N_h}\lambda _{h,l}\alpha _{h,l}\Delta V_l}, \end{aligned}$$
(11.1)
$$\begin{aligned}&\hat{\varvec{n}}_{h}=-\frac{{\varvec{n}}_h}{||{\varvec{n}}_h||}, \end{aligned}$$
(11.2)

where \(\hat{\varvec{n}}_h\) points from the solid interior to the surrounding fluid. Once the unit normal is known, the tangent vector, \(\hat{\varvec{t}}_{h}\) can be easily computed as well as the bi-normal vector, \(\hat{\varvec{b}}_{h}=\hat{\varvec{n}}_{h} \times \hat{\varvec{t}}_{h}\). Additional information about the procedure for computing tangent, normal, and bi-normal vectors is provided in [40].

A local, orthogonal coordinate system, (\(\xi ,\zeta ,\eta )\), is considered according to the tangent, bi-normal and normal directions to the interface, respectively, as shown in Fig. 2. In correspondence of each Lagrangian position located on the fluid–solid interface, \(\varvec{X}_h\), a probe of length \(l=2\Delta _f\) is defined along the normal vector [51]. The fluid pressure is extrapolated at probe root point, R, according to the following expressions [51]:

$$\begin{aligned}&p |_R = p|_T+\frac{1}{2}\left[ \frac{\partial p}{\partial \eta }{\bigg |_R}+\frac{\partial p }{\partial \eta }{\bigg |_T}\right] l, \end{aligned}$$
(12.1)
$$\begin{aligned}&\frac{\partial p}{\partial \eta }{\bigg |_R}\approx \frac{D{\varvec{u}}}{D t}{\bigg |_R}\cdot \hat{\varvec{n}}_h\approx \frac{d{\varvec{U}}_h}{d t}\cdot \hat{\varvec{n}}_h, \end{aligned}$$
(12.2)
$$\begin{aligned}&\frac{\partial p}{\partial \eta }{\bigg |_T}=\nabla p|_T \cdot \hat{\varvec{n}}_h, \end{aligned}$$
(12.3)
$$\begin{aligned}&p|_T=\sum _{i,j,k} p_{i,j,k} \delta _\Delta (\varvec{x}_{i,j,k}-\varvec{X}_T) \Delta _f^3, \end{aligned}$$
(12.4)

where the subscript T denotes the probe tip and the pressure gradient \(\nabla p|_T\) is computed via the central finite difference scheme on the stencil sketched in Fig. 2 for the two-dimensional case. The spacing of the stencil is set to \(\Delta _f\), whereas the pressure is computed on each node of the stencil by an interpolation based on a regularized Dirac delta function [40]. The computation of the shear stresses at the probe root, R, is based on the velocity gradient evaluated at the probe tip, T, and computed on the same stencil used for the pressure field:

$$\begin{aligned}&\frac{\partial u_{\xi }}{\partial \eta }{\bigg |_R} = \nabla {\varvec{u}}{|_T}\cdot \hat{\varvec{t}}\cdot \hat{\varvec{n}}, \end{aligned}$$
(13.1)
$$\begin{aligned}&\frac{\partial u_{\zeta }}{\partial \eta }{\bigg |_R} = \nabla {\varvec{u}}{|_T}\cdot \hat{\varvec{b}}\cdot \hat{\varvec{n}}, \end{aligned}$$
(13.2)
$$\begin{aligned}&\frac{\partial u_{\eta }}{\partial \eta }{\bigg |_R} = \nabla {\varvec{u}{|_T}}\cdot \hat{\varvec{n}}\cdot \hat{\varvec{n}}. \end{aligned}$$
(13.3)

It is worth remarking that the equations above hold only under the assumption that the velocity field near the solid–fluid interface varies linearly [52]. Finally, the stress components expressed in the local frame of reference are computed as:

$$\begin{aligned}&\tau _{\xi } = \mu \frac{\partial u_{\xi }}{\partial \eta }{\bigg |_R}, \end{aligned}$$
(14.1)
$$\begin{aligned}&\tau _{\zeta } = \mu \frac{\partial u_{\zeta }}{\partial \eta }{\bigg |_R}, \end{aligned}$$
(14.2)
$$\begin{aligned}&\tau _{\eta } = \mu \frac{\partial u_{\eta }}{\partial \eta }{\bigg |_R}-p|_R. \end{aligned}$$
(14.3)

The overall stress, \({\varvec{\tau }}_h\), can then be expressed in the global frame of reference, and the forces per unit volume exerted by the fluid on the solid at the Lagrangian position \({\varvec{X}}_h\) can be evaluated as:

$$\begin{aligned}&{\varvec{F}}_h=-{\varvec{\tau }}_h \frac{A_h}{\Delta s^3}, \end{aligned}$$
(15)

where the area \(A_h\) is the actual area of the solid surfaces evaluated at the beginning of the simulation divided by the total number of the Lagrangian solid particles located onto the fluid–solid interface. It is worth remarking that the Navier–Stokes equations are advanced from step \(r-1\) to step r given the solid–fluid interface velocity and position at step \(r-1\), as reported in Algorithm 1. This approach is known as explicit coupling. The use of an explicit, weak-coupling scheme between the Navier–Stokes and peridynamic equations affects the temporal accuracy of the algorithm and restricts the stability limit for low-density-ratio problems due to the added-mass effect [53]. Nonetheless, it allows for much easier implementation and requires less computational cost per time step. In the present case, the density ratio is high enough to avoid instability. For additional details about the whole procedure, as well as interface definition and tracking, the reader is referred to Dalla Barba and Picano [40] and Yang and Balaras [49,50,51,52].

3 Test-case description

The direct numerical simulation of a three-dimensional turbulent channel flow confined between a rigid plane wall and a flattened bed of a linear-elastic and brittle material is addressed. The Eulerian computational domain is a rectangular box extending for \(Lx\times Ly\times Lz=3h\times 1.5h\times 1.125 h\) in the flow, span-wise, and wall-normal directions, respectively. The streambed is represented as a rectangular block constrained to the lower wall of the computational domain, which is assumed to act as an impermeable and rigid substrate, as sketched in Fig. 3. The turbulent flow initially develops in the rectangular channel of height h confined between the upper wall of the domain and the initial bed surface. As the erosion of the streambed advances, the section of the channel can freely increase up to a maximum height of 1.125h, as the fluid flow approaches the rigid and impermeable substrate.

Fig. 3
figure 3

Schematic of the computational domain. The zone highlighted in light grey shows the initial shape of the streambed. The region highlighted in dark grey shows the ghost solid to which the fixed constraint is applied (color figure online)

Full size image

The discretization of the Eulerian domain consists of a Cartesian and uniform grid of \(N_x\times N_y\times N_z = 288\times 144\times 108\) nodes. The streambed is discretized using a total of \(N_p=580608\) cubic Lagrangian particles distributed, in the initial configuration, according to the nodes of the Eulerian grid: the number of particles along the flow, span-wise, and wall-normal direction is set to \(Np_x\times Np_y\times Np_z = 288\times 144\times 14\). The bond-based peridynamic model for three-dimensional problems is used, setting the horizon to three times the Eulerian grid spacing, \(\delta /h = 3\Delta x/h =2.1\cdot 10^{-2}\). No-slip and no-penetration boundary conditions are prescribed to the upper and lower sides of the computational domain, whereas periodic boundary conditions are used along the flow and span-wise directions. A fictitious pressure gradient is used to force the turbulent flow along the x direction such that a constant bulk Reynolds number and a constant mass flow rate are enforced. The forcing is suppressed for the ghost fluid located in the regions occupied by the solid material. A fixed constraint is applied to a ghost layer of \(Np_x\times Np_y\times Np_z = 288\times 144\times 3\) solid particles extending outside of the lower base of the computational domain as sketched in Fig. 3. The initialization of the simulation is performed starting from a fully developed turbulent flow. The solid bed is let deform disabling the bond break up by applying to it a fictitious damping force-field proportional to the deformation velocity until a statistically stationary equilibrium configuration is achieved with the fluid stresses. The bond break up is then enabled, and the simulation is run over the time range \(t/\tilde{t}\in [0,45]\) with a fixed time step, \(\Delta t/\tilde{t}=3.5\cdot 10^{-3}\), \(\tilde{t} = h/U_b\) being the reference time scale of the fluid and \(U_b\) the bulk, axial velocity of the flow. The physical parameters of the fluid and the solid are provided in Table 1.

Table 1 Physical parameters expressed in non-dimensional units: bulk Reynolds number, \(Re_b=U_b h/\nu _f\), friction-velocity Reynolds number, \({\mathrm{Re}_\tau }=u_\tau h/(2\nu _f)\), Young’s modulus, E, critical fracture energy release rate, \(G_0\), solid to fluid density ratio, \(\rho _s/\rho _f\), and Poisson’s ratio of the solid material, \(\nu _s\)
Full size table

The present numerical study focuses on the effect of turbulence and fluid stresses on the scouring and scour-formations on a soft and brittle streambed. To highlight these aspects, the properties of the solid material were chosen such that the ultimate shear strength of the channel bed is approximately 1.5 times the mean fluid shear stress acting on the solid walls of the channel in the initial stage of the simulation, \(\tau _w\) (steady flow without fracturing). This aspect will be further addressed in Sect. 4. It is worth remarking that, in the present work, the stress components acting on the deformable streambed are computed according to Eq. refeq:revsps2000 and transformed into the global frame of reference, whereas the stress acting on the upper channel wall is computed by the evaluation of local pressure and velocity gradients. Since the normal, tangent and bi-normal vectors to the solid–fluid interface are always computable, this approach is used even after the channel bed has been eroded. Gravitational acceleration and buoyancy are neglected, as well as the impact forces generated by solid fragments on the streambed. These choices remove the possibility to account for the settling and gravity-driven preferential concentration of sediments near the channel bed, as well as abrasion and impacts. Nonetheless, they enable us to highlight the effects of turbulent fluctuations on bedforms and bed erodibility. It is also worth remarking that a certain amount of solid fragments and single material particles completely detaches from the immersed solid layer. The effects of detached material particles (single ones with no interactions) are neglected in the simulation. These particles are entrained and transported by the carrier fluid as passive tracers for qualitative visualization purposes only and do not affect the dynamics of the fluid phase. Over the simulated interval of time, the average volume fraction of the eroded solid phase entrained and transported by the carrier stream is found to be \(2.4\times 10^{-3}\), the corresponding mass fraction being \(1.2\times 10^{-2}\). Hence, the effect of the removed volume and mass on the system is negligible in terms of mass and volume flow rates. Under these conditions, the major effect of removing from the simulation completely detached particles concerns neglecting the momentum exchanged by the latter with the carrier phase, which, under the considered mass and volume fractions, is a reasonable hypothesis. Moreover, since the focus of the paper is on the scouring process itself, more than on the effect of eroded material on the flow, this hypothesis is not restrictive for our purposes. It is also worth remarking that, since the entire dynamical evolution of the solid streambed occurs in the linear-elastic regime, the brittle and linear-elastic model employed in the present work is suitable to represent the mechanical properties of the solid. To evaluate the intensity of the deformation that the streambed undergoes within the simulated interval of time we computed a posteriori the intensity of the bond stretches over the whole simulated range of time: the maximum bond stretch is found to be of the order of \(6.5\times 10^{-2}\), whereas its average value is \(9.0\times 10^{-3}\). This confirms that the evolution of the solid occurs entirely in the linear-elastic regime.

4 Simulation results and discussion

4.1 Validation of the fluid solver

In this Section a validation of the fluid solver is provided in order to proof the adequacy of the employed methodology and grid resolution in addressing the considered problem. For what concern the validation of the solid solver (dynamic and static test cases, as well as fracture reproduction) the reader is referred to Dalla Barba and Picano [40].

Fig. 4
figure 4

a Mean axial velocity of the flow, \(\langle u^+\rangle \), versus normal distance to the wall, \(z^+\), expressed in internal units for the upper boundary of the computational domain and the surface of the streambed. b Root-mean-square velocity fluctuations, \(\sqrt{\langle u'u'\rangle }\), \(\sqrt{\langle v'v'\rangle }\) and \(\sqrt{\langle w'w'\rangle }\), normalized by the friction velocity, \(u_\tau \). (c)(d) Two-point correlations \(R^y_{u'u'}\), \(R^y_{v'v'}\), and \(R^y_{w'w'}\) versus spanwise separation, \(\Delta y^+\), expressed in internal units, at \(z^+=5.39\) and \(z^+=149.3\). The statistics are compared with the results by Kim et al. [54] at \(Re_\tau =180\)

Full size image

To provide a specific validation for the considered test case, in addition to the benchmarking tests referenced in Dalla Barba and Picano [40], we consider three different statistics: the axial velocity profile expressed in internal units, provided in Fig. 4a, the root-mean-square velocity fluctuations, \(\sqrt{\langle u'u'\rangle }\), \(\sqrt{\langle v'v'\rangle }\), and \(\sqrt{\langle w'w'\rangle }\), normalized by the friction velocity, \(u_\tau \), shown in Fig. 4b, and the two-point correlations \(R^y_{u'u'}\), \(R^y_{v'v'}\), and \(R^y_{w'w'}\) versus spanwise separation, \(\Delta y^+\), expressed in internal units, shown in Fig. 4c, d. All the statistics have been computed in the initial stages of the simulation, within the range of time \(t/\tilde{t}\in [0,10]\). For what concerns \(\langle u^+\rangle \) in Fig. 4a, the trends related to the upper (rigid) and lower (deformable) walls of the channel are similar, except for a small velocity overshoot in the lower-wall velocity profile. The absence of significant differences between the two profiles is due to the overall small deformation of the channel in the considered range of time. The numerical curves are compared to the linear law, \(\langle u^+\rangle =z^+\), in the viscous sublayer and to the logarithmic law, \(\langle u^+\rangle =1/k\ ln(z^+)+C\), in the log-region, the von Kármán constant being \(k=0.4\), whereas \(C=5.5\). The agreement between the trends of the theoretical and numerical curves is excellent. To verify the mesh resolutions, both the velocity profile and fluctuations have been recomputed using a finer mesh on the same computational domain: \(N_x\times N_y\times N_z = 504\times 262\times 168\). No significant differences can be observed between the data sets, confirming that the adopted mesh resolution is adequate to fully resolve the fluid stream. The two-point correlations \(R^y_{u'u'}\), \(R^y_{v'v'}\), and \(R^y_{w'w'}\) for two different distances from the channel bed, Fig. 4c, d, are compared with the reference data by Kim et al. [54] at \(Re_\tau =180\). It is worth noting that the position of the minima of the statistics is congruent with low-Reynolds number simulations available in archival literature, but some differences subsist between the present and reference data due to the different Reynolds numbers.

4.2 Phenomenological description of turbulence-driven scouring

Fig. 5
figure 5

Snapshots of the morphology of the channel bed at four different time steps. Panel a: \(t_1/\tilde{t} = 16.75\), panel b: \(t_2/\tilde{t} = 25.5\), panel c: \(t_3/\tilde{t} = 34.25\), and panel d: \(t_4/\tilde{t} = 43.0\).

Full size image
Fig. 6
figure 6

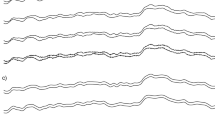
Snapshots of the turbulent structures of the flow visualized by means of the Q-criterion (iso-surfaces \(Q = 1.0\)) in the left side of the turbulent channel, \(0.75<y/h<1.5\). The panels provide the contour plot of the iso-level of the axial component of the fluid velocity, u and the damage level in the solid, \(\Phi \), together with the solid fragments transported by the carrier fluid. Panel a: \(t_1/\tilde{t} = 16.75\), panel b: \(t_2/\tilde{t} = 25.5\), panel c: \(t_3/\tilde{t} = 34.25\), and panel d: \(t_4/\tilde{t} = 43.0\)

Full size image

Figure 5 provides a visualization of the surface of the streambed evaluated at four different time levels, whereas, at the same instants, Fig. 6 shows the entire computational domain. In Fig. 6 the turbulent structures of the flow are visualized in the left side of the channel employing the Q-criterion (iso-surfaces \(Q = 1.0\)), contoured by the iso-levels of the axial velocity field of the fluid, u. A visualization of the sediment fragments removed by the erosion and entrained by the turbulent stream is also provided along with the iso-damage levels in the solid bed. The damage level consists of a scalar field providing information about the local damage status of a brittle peridynamic material and is defined, for a given Lagrangian position \(\varvec{X}_h\), as in the following:

$$\begin{aligned} \phi _h=\frac{\sum _{l=1}^{N_h} \lambda _{h,l}\alpha _{h,l}\Delta V_l}{\sum _{l=1}^{N_h} \alpha _{h,l}\Delta V_l}. \end{aligned}$$
(16)

According to Eq. (16), the damage level evaluated at a given Lagrangian position \(\varvec{X}_h\) can be interpreted as the ratio between the number of broken bonds and the overall number of bonds involving the considered material point. The ratio is computed weighting the status of each bond by the volume of the material points involved in each pairwise interaction. The early stages of the erosion process are characterized by the formation on the channel bed of many confined zones where the material is highly damaged. In these areas, we observe the progressive detachment of small solid fragments and the formation of shallow scour-holes as evident in Figs. 5a and 6a. The detachments involve small fragments that rapidly break up producing small size grains (single peridynamic particles) which are entrained and transported downstream by the turbulent flow. It is worth noting that the scour-holes are preferentially distributed along two bands elongating in the flow direction and centered around the span-wise positions \(y/h\simeq 0.5\) and \(y/h\simeq 1.25\), respectively. These regions on the channel bed correspond to the location of two main stationary turbulent stripes in the flow. The reason for this preferential distribution of the shallows abrasions of the streambed will be addressed in the following. As the erosion process advances, the number of the damaged areas increases along with their extension, until we observe the formation of two main grooves originating from the coalescence of smaller scour-holes on the channel bed as can be observed in Figs. 5c and 6c. At this step, the depth of eroded zones starts to progressively increase until, at time \(t/\tilde{t}\simeq 38.0\), the rapid formation of a deep depression is observed in the region of the bed delimited by \(1.75<x/h<2.25\) and \(0<y/h<0.9\), as reported by Figs. 5d and 6d. It should be remarked that the mean intensity of the fluid stresses acting on the solid bed layer is not high enough to cause a global bed detachment from the impermeable and rigid substrate. In these conditions, the formation of abrasions and scour-holes is caused by turbulent fluctuations in the flow that locally enhance the intensity of the wall-stresses producing localized damages. As will be addressed in the following, the accumulation of damages in time drive the scouring of the channel bed by means of a turbulence-driven fatigue mechanism. The scour structures observed in our numerical results are qualitatively similar to the experimental observation by Kothyari and Jain [55]. In their setup, the authors focus on the incipient motion characteristics of cohesive sediment mixtures containing gravel in a tilting flume. We observe, numerically, three types of conditions of incipient motion which are observed also experimentally. These different mechanisms are observed both at different times and locations, as sketched in Fig. 7. The first mechanism is referred to as pothole erosion: the detachment of material initiates in the form of individual particles and gives rise to potholes over the bed surface at different locations, see Fig. 7a. The second is called mass erosion and consists of the detachment of chunks of varying sizes that appear to be ripped, or torn off, from the bed surface, see Fig. 7b. The last is referred to as line erosion and consists of the detachment of thin flakes from the sediment surface. The material removal continues and spreads both longitudinally and laterally, but more in the longitudinal direction, as can be observed in Fig. 7c. For a comparison with the reference experimental observations, the reader is referred to Figs. 4, 5, and 6 in Kothyari and Jain [55]. Even if the operative conditions and the properties of the sediment involved are quite different, we believe that the mechanisms underlying the bed erosion in the experimental test case and our numerical simulation are very similar.

Fig. 7
figure 7

a Detachment of material in the form of pothole erosion. The numerical results are comparable to Fig. 4 of Kothyari and Jain [55]. b Localized initiation of detachment in the form of mass erosion. The numerical results are comparable to Fig. 6 of Kothyari and Jain [55]. c Detachment of material along linear regions. The numerical results are comparable to Fig. 5 of Kothyari and Jain [55]

Full size image

4.3 Volumetric erosion rate

To detail by a quantitative point of view the progress of the erosion process, we define an eroded volume ratio, \(\mathcal {E}(t)\), as the overall volume of the material removed by the erosion from the beginning of the simulation up to time t, \(V_r(t)\), normalized by the overall volume removed during the simulated interval of time, \(V_r(t_f)\), with \(t_f/\tilde{t}=45\). The latter is around \(9.7\%\) of the solid material initially enclosed in the computational domain (\(0.125 L_x L_y h\)). A volumetric erosion rate, e(t), can then be defined as the time-derivative of \(\mathcal {E}(t)\):

$$\begin{aligned}&\mathcal {E}(t) = \frac{V_r(t)}{V_r(t_f)}, \end{aligned}$$
(17)
$$\begin{aligned}&e(t) = \frac{d\mathcal {E}(t)}{dt}. \end{aligned}$$
(18)

The volumetric erosion rate and the eroded volume ratio are provided in Fig. 8. A progressive speed-up of the erosion is observed. In the early phases of the process, no material is removed from the streambed, \(t/\tilde{t}\in [0.0,10.0]\). During this interval of time, only local damages originate on the bed surface without causing any fragmentation. The volumetric erosion is null as well as the eroded volume ratio. Nonetheless, the damage level progressively increases in time due to the cumulative effects induced by local turbulent fluctuation on the channel bed. The detachment of solid fragments starts around \(t/\tilde{t}\simeq 10.0\). We find by polynomial fitting that for \(t/\tilde{t}\in [10.0,38.0]\) the eroded volume ratio, \(\mathcal {E}(t)\), varies quadratically with time, and, consequently, the erosion rate grows linearly as sketched in Fig. 8:

$$\begin{aligned}&\mathcal {E}(t) \approx K_e t^2, \end{aligned}$$
(19)
$$\begin{aligned}&e(t) \approx 2 K_e t, \end{aligned}$$
(20)

the constant \(K_e\) expressed in non-dimensional units being \(K_e=4.5 \cdot 10^{-4}\). Approximately at time \(t/\tilde{t}\simeq 38\) the erosion rate and the eroded volume ratio suddenly increase. This acceleration is caused by a random event that produces the detachment and the fragmentation of a large portion of the channel bed as will be addressed in the following Sections.

Fig. 8
figure 8

Temporal evolution of the eroded volume ratio and volumetric erosion rate of the streambed defined according to Eqs. (17) and (18). All the quantities are non-dimensional

Full size image

The acceleration of the erosion process can be explained considering that the scouring of the channel bed enhances in turn the erosion rate by perturbing the flow over the scour structures and increasing the intensity of the stresses acting on the channel bed. Indeed, as will be discussed in the following, the presence of depressions and protrusions generated by the erosion of the channel bed promotes the formation, at different length scales, of turbulent structures that persist over these regions. In turn, these coherent structures enhance the erosion rate of the streambed by locally increasing stresses on the bottom surface.

4.4 The role of turbulence in the formation of scour-holes

The formation of scouring structures on the flattened channel bed can be put in relation to the action of the turbulent fluctuations of the flow. High-intensity turbulent fluctuations can occur at random instants and positions over the bottom surface, enhancing the bottom-stresses. If the intensity of the fluid-induced stresses is high enough to overcome the ultimate stress of the brittle streambed, local damage is produced, and the formation of micro-cracks on the initially flat surface occurs. As will be addressed in detail, the damage of the solid might occur in the event of two phenomena. The former relies on a shear-stress driven damage occurring where the fluid-induced shear stress exceeds the ultimate shear strength of the material. The latter consists of tensile damage that rises if the traction stress exerted by the fluid on the solid bed overcomes the ultimate tensile strength. Once the solid bed is locally damaged, its local strength drops, and the propagation of cracks can be induced by lower-intensity loads. Therefore, the local damage accumulates in time via the formation and branching of micro-cracks that can finally lead to the local break up and detachment of solid fragments. The process essentially consists of a turbulence-driven fatigue failure of the brittle sediment layer and results in the formation of shallow scour-holes on the channel bed.

Fig. 9
figure 9

Visualization of the near-wall turbulent structures of the flow by means of the Q-criterion (iso-surfaces \(Q=5\)). The iso-surfaces are plotted only within \(z/h<0.150\). Panel a shows the whole streambed. The iso-levels of Q are contoured by the axial component of the flow velocity, u, whereas the surface of the streambed is contoured by the damage level, \(\phi \). Panel b provides a zoom on \(0.25<x/h<1.5\) and \(0.25<y/h<0.75\). The iso-levels of Q are contoured by the axial component of the flow velocity, u, whereas the surface of the streambed is contoured (log-scale) by the magnitude of the wall stress, \(||\tau ||=\sqrt{\tau _{zx}^2+\tau _{zy}^2+\tau _{zz}^2}\), normalized by the mean wall stress computed on the solid walls of the channel in the initial stage of the simulation (steady flow without fracturing), \(\tau _w\)

Full size image

The presence of scour-holes can alter the local flow structure enhancing, in turn, the intensity of turbulent fluctuations and wall stresses acting on their proximity. Figure 9 provides a visualization of the small-scale vortical structures of the flow in the proximity of the channel bed, \(z/h<0.150\), by means of the Q-criterion at time \(t/\tilde{t}=25.5\) and \(t/\tilde{t}=27.5\). The left panel, Fig. 9a, visualizes the iso-surfaces \(Q=5\) contoured by the axial velocity of the flow, u, along with the damage level in the solid material, \(\phi \). The right panel, Fig. 9b, provides a zoom of the iso-surfaces \(Q=5\) on \(0.25<x/h<1.5\) and \(0.25<y/h<0.75\) contoured by the axial velocity of the flow, u, along with the magnitude of the stress acting on the solid surface, \(||\tau ||=\sqrt{\tau _{zx}^2+\tau _{zy}^2+\tau _{zz}^2}\), normalized by the mean shear stress computed on the solid walls of the channel in the initial stage of the simulation (steady flow without fracturing). From a qualitative point of view, it can be observed that small-scale turbulent structures develop over the irregularities of the channel bed, whereas flat regions are depleted of intensive near-wall vortices. These vortical cells form over the narrow, downstream borders of the scour-holes and tend to persist over these areas. It is worth remarking that some similarities of these small-scale span-wise rollers subsist with the bed-penetrating Kelvin–Helmholtz vortices recently described in the work of Guan et al. [56]. The presence of these coherent structures enhances the magnitude of the fluid stresses acting on the streambed. As evidenced in Fig. 9b, the stress-peaks are located on the narrow downstream borders of the scour-holes, in the immediate proximity of the coherent structures stationing over the irregular hole boundaries. In these restricted areas, the stress magnitude can locally grow up to twenty times the mean shear stress computed on the rigid flattened wall of the channel, \(\tau _w\). The stress peak induced on the border of the scour-holes enhances, in turn, the erosion rate of the channel bed and is responsible for the quadratic increment of the eroded volume ratio reported in Fig. 8a. In particular, the irregular scour-holes on the streambed cause a spread of the probability distribution of the fluid-induced stresses acting on it, as will be addressed in Sect. 4.6. This phenomenology leads to a progressive expansion of the scoured regions in the downstream direction by the fragmentation of the downstream borders of the shallow abrasions. As a result, we observe the formation of the two grooves on the channel bed by the coalescence of shallow scour-holes propagating in the downstream direction. In analogy with the coupling between the dynamics of small-scale scouring abrasions and small-scale coherent structures of the flow, the large-scale irregularities of the streambed channelize the flow, leading to the formation of two turbulent stripes that persist over these eroded areas. As a result of this coupled process, the groove pattern results to be stable. Once the extension of the grooves has covered the whole computational box in the streamwise direction, the erosion process proceeds mainly in the other directions, whereas the formation of additional shallow abrasions on the remaining flat regions stops.

Fig. 10
figure 10

Streamlines of the turbulent flow starting from \(x/h=0\), \(0<y/h<0.9\), \(0.1<z/h<0.15\) at time, \(t/\tilde{t}=39.5\). The streamlines are contoured by the flow axial velocity, u, whereas the streambed is contoured by the damage level, \(\phi \)

Full size image

The effects of the bed morphology on the large-scale structure of the flow is put in evidence in Fig. 10, which provides the three-dimensional streamlines starting from \(x/h=0\), \(0<y/h<0.9\), \(0.1<z/h<0.15\) at time, \(t/\tilde{t}=39.5\). At this time level, the shallow scour-holes on the channel bed have completely coalesced and given rise to the two grooves spanning along the whole channel length in the downstream direction. Moreover, as previously outlined, a deep depression located in \(1.75<x/h<2.25\), \(0<y/h<0.9\) has been scoured by the flow. The channelization of the flow by the shallow grooves on the channel bed is clearly visible: the streamlines follow straightly the right side groove on the channel bed, without escaping from this region. Moreover, the presence of a large-scale recirculation can be observed over the deep depression on the right side of the channel. This recirculating cell tends to further increase the local fluid stresses acting on the streambed and thus enhancing the volumetric erosion rate in its proximity.

Fig. 11
figure 11

Contour plots of the instantaneous depth of eroded regions on the streambed, \(\Delta z_w/z_{w,0}\), and wall stress components, \(\tau _{zx}\) and \(\tau _{zz}\), evaluated at two different time levels: panels a, c, and e refer to \(t/\tilde{t}=29.5\), whereas panels b, d, and f refer to \(t/\tilde{t}=41.5\)

Full size image

The correlation between the distribution of the wall stresses and the scour structures on the channel bed can be observed in Fig. 11, providing the contour plots of the stress components, \(\tau _{zx}\) and \(\tau _{zz}\) at time \(t/\tilde{t}=29.5\) and \(t/\tilde{t}=41.5\). The stress peaks are located on the downstream borders of the shallow irregularities of the channel bed, while minima are localized immediately upstream. This stress distribution is congruent with the presence of small-scale vortices over the shallow scour formations of the streambed. An analogous stress pattern is observed for the large-scale hole located in the bed region \(1.75<x/h<2.25\), \(0<y/h<0.9\) and surmounted by the large-scale recirculating cell.

4.5 Large-scale morphology of the streambed

To investigate the evolution of the large-scale morphology of the channel bed we consider the following quantities: the mean depth of erosion, \(\langle \Delta z_w\rangle \), and the mean stresses, \(\langle \tau _{zx}\rangle \), \(\langle \tau _{zy}\rangle \), and \(\langle \tau _{zz}\rangle \) computed at different time steps either along the streamwise or the spanwise direction. The depth of erosion, \(\langle \Delta z_w\rangle \), is defined, at a given location and time, as the variation of the thickness of the sediment with respect to its initial thickness, \(z_{w,0}\). Figure 12 provides \(\langle \Delta z_w\rangle \), \(\langle \tau _{zx}\rangle \), \(\langle \tau _{zy}\rangle \), and \(\langle \tau _{zz}\rangle \) computed at three different time steps, \(t/\tilde{t} = 29.5\), \(t/\tilde{t} = 37.5\), and \(t/\tilde{t} =41.5\). For what concerns the averaging over the span-wise direction (right side panels of Fig. 12), the instantaneous surface of the solid bed is divided into 80 finite-size slices of width \(S_x/h=0.0375\), with \(0<y<0.9h\). The instantaneous depth of erosion and the resulting fluid-dynamic stresses acting on the solid are computed on each of these slices. A similar procedure is adopted for the averaging along the x direction using 40 finite-size slices of width \(S_y/h=0.0375\), with \(0<x<3.0h\) (left side panels of Fig. 12). It is clearly visible how the irregularities of the channel bed relate to the distribution of the fluid stresses in the corresponding region. In particular, protrusions of the solid surface act locally as obstacles to the flow, inducing the formation of coherent structures. These vortices induce positive traction stresses \(\tau _{zx}\) and \(\tau _{zz}\) downstream of the surface protrusions and negative compression stresses upstream of the obstacles. This mechanism is compatible with the massive detachment of material observed at \(t/\tilde{t}\simeq 38.0\).

Fig. 12
figure 12

x-averaged and y-averaged depth of erosion, \(\langle \Delta z_w\rangle \) and mean stresses, \(\langle \tau _{zx}\rangle \), \(\langle \tau _{zy}\rangle \), \(\langle \tau _{zz}\rangle \), as a function of y and x, respectively. The statistics refer to the following times: \(t/\tilde{t}=29.5\) for a and b, \(t/\tilde{t}=37.5\) for c and d, and \(t/\tilde{t}=41.5\) for e and f. The reference scale for the stresses is the mean shear stress computed on the solid walls of the channel in the initial stage of the simulation (steady flow without fracturing). The reference length for the depth of erosion is the initial bed thickness, \(\Delta z_{w,0}\)

Full size image

A bump is evident in \(1.75<x/h<2.4\) in the left side of panel 12(a), whereas it disappears in panel 12(b). This peak is located between two consecutive shallow scoured regions located in the right-side of the channel bed; moreover, the height of this protrusion at time \(t/\tilde{t}=29.5\), is, on average, the highest of the channel bed. The presence of this formation causes, due to the mechanisms outlined above, an increment of the local fluid stresses in the downstream area that, in turn, causes the destruction of the bump. At time step \(t/\tilde{t}=37.5\) the bump is disappearing. On average, the presence of the valley further enhances the fluid stresses as evidenced in Fig. 12b. This mechanism is responsible of the deep scour-hole visible in the right side of the channel bed after time \(t/\tilde{t}\simeq 38\).

4.6 Probability density function of stresses

We showed how small-scale coherent structures and large-scale recirculating cells exist near the bed surface and mutually interact with the scouring process of the channel bed. In the following, it will be discussed how the stresses acting in the proximity of the scour-holes are sufficiently intense to cause the propagation of the fracture in the downstream direction leading to an overall speed-up of the erosion process and governing the morphology of the streambed. The phenomenology described in Sects. 4.4 and 4.5 can be highlighted considering the probability density functions (PDFs) of the fluid stresses and the related cumulative distribution functions (CDFs). Figure 13a, c, e provides the PDFs of the stress components expressed in the global coordinate system, \(\tau _{zx}\), \(\tau _{zy}\), and \(\tau _{zz}\), computed in the initial stage of the erosion process, where the fluid–solid interface preserves a flattened shape, \(t/\tilde{t}\in [0.0,18.0]\). In this regime, no appreciable differences can be found between the PDFs computed on the upper, rigid wall of the channel and the ones computed on the streambed. Nonetheless, as the depth of eroded areas increases, a significative spread out of the PDFs tails is observed for the erodible bed as can be seen in Fig. 13b, d, f showing the same statistics computed over the time range \(t/\tilde{t}\in [18.0,36.0]\). The spreading of the PDF tails confirms how the formation of irregularities on the bed surface enhances the intensity of turbulent fluctuations, and hence, of the local wall stresses causing, as a result, a speed-up of the surface erosion.

Fig. 13
figure 13

Probability density functions (PDFs) of the fluid-dynamic stresses acting on the bed surface (blue lines) and the upper wall of the channel (red lines). Panels a, c, and d provide the PDFs of the stresses computed in the time range \(t/\tilde{t}\in [0.0,18.0]\) where only minor damaged areas appear on the bed surface, whereas panels b, d, and e provide the PDFs computed in the time range \(t/\tilde{t}\in [18.0,36.0]\) where highly damaged areas are observed (color figure online)

Full size image
Fig. 14
figure 14

a Two dimensional schematic representation of unloaded, pure traction, and pure shear loading condition in a discrete peridynamic medium. b Representation of the bond connecting \(\varvec{X}_1\) to \(\varvec{X}_3\) under pure shear conditions

Full size image

To further highlight the mechanisms described above, we compare the intensity of the fluid stresses with the ultimate strength of the channel bed. Due to the prescribed mechanical properties of the material composing the submerged sediment, the solid streambed breaks up in a brittle manner where the fluid induces a shear stress state, or a positive traction state, that overcomes the ultimate shear or tensile strength of the material, respectively. An estimation of the ultimate tensile strength of a brittle peridynamic material, \(\sigma _u\), can be computed considering that, in pure traction conditions, the maximum bond stretch is aligned to the direction of the applied tensile load and is equivalent to the linear deformation of the material, \(\epsilon \), as sketched in the center panel of Fig. 14a. A fracture occurs when the maximum bond stretch reaches the limit bond stretch, \(s_0\), as sketched in the central panel of Fig. 14, such that:

$$\begin{aligned} \sigma _u=E\epsilon =E s_0=\sqrt{\frac{5EG_0}{6\delta }}. \end{aligned}$$
(21)

In an analogous fashion, a raw estimation of the ultimate shear strength, \(\tau _u\), can be computed considering the maximum stretch within the bonds pertaining to the family of a given peridynamic particle in pure-shear loading conditions. As shown in the right panel of Fig. 14a, in pure-shear the maximum stretch is achieved along the diagonal bond connecting \(\varvec{X}_1\) to \(\varvec{X}_3\). According to Fig. 14b, for small deformations of the body, the bond elongation is:

$$\begin{aligned} ||\varvec{X}_3-\varvec{X}_1||\simeq \sqrt{\frac{\Delta _s^2}{\mathrm{cos}^2(\gamma )}+\Delta _s^2 -\frac{2\Delta _s^2}{\mathrm{cos}(\gamma )}\mathrm{cos}(90^\circ +\gamma )} \simeq \Delta _s\sqrt{2\left( 1+\gamma \right) }, \end{aligned}$$
(22)

where \(\gamma \) is the angular deformation and \(\Delta _s\) the spacing of the peridynamic nodes in the non-deformed configuration of the body (uniform and equispaced in the present work). Since the unloaded bond length is \(||\varvec{X}_{3,0}-\varvec{X}_{1,0}||=\sqrt{2}\Delta _s\), with \(\Delta _s\) the solid grid spacing in the undeformed configuration of the body, the maximum bond stretch within the family of the considered particle results:

$$\begin{aligned} s_\mathrm{max}=\frac{||\varvec{X}_3-\varvec{X}_1|| -||\varvec{X}_{3,0}-\varvec{X}_{1,0}||}{||\varvec{X}_{3,0} -\varvec{X}_{1,0}||}\simeq \sqrt{1+\gamma }-1. \end{aligned}$$
(23)

By this approach, it is possible to estimate the limit angular deformation leading to \(s_{max}=s_0\) and hence to the failure of the bond:

$$\begin{aligned} \gamma _u\simeq s_0(s_0+2). \end{aligned}$$
(24)

The ultimate shear strength of the material can then be estimated as:

$$\begin{aligned} \tau _u=G\gamma _u=Gs_0(s_0+2)=\frac{E}{2(1+\nu _s)}s_0(s_0+2), \end{aligned}$$
(25)

with G the shear modulus of the material. In the present case, we obtain \(\sigma _u/\tau _w\simeq 1.84\) and \(\tau _u/\tau _w\simeq 1.5\). We can define a turbulent event as the occurrence of a localized turbulent motion in the fluid that produces on the wall of the channel a certain shear stress, \(\tau =\sqrt{\tau _{zx}^2+\tau _{zy}^2}\), and wall-normal stress, \(\sigma =\tau _{zz}\), at a given location and time. In this frame, the turbulent events capable to produce a fracture are those causing a stress state on the solid surface of the channel bed, \(\tau >1.5\tau _w\) or \(\sigma >1.84\tau _w\). To evaluate the probability of a new fracture to form, we consider separately the fracturing induced by high shear-stress events and fracturing driven by high wall-normal stress events. It is possible to evaluate the fracture probability according to the cumulative distribution functions provided in Fig. 15.

Fig. 15
figure 15

Cumulative density functions (CDFs) of the wall-tangent stresses \(\tau =\sqrt{\tau _{zx}^2+\tau _{zy}^2}\) and wall-normal stresses, \(\sigma =\tau _{zz}\), acting on the bed surface. The red lines provide the CDFs for the upper wall of the channel, whereas the blue ones for an erodible streambed. Panels a and b refer to the CDFs of the stresses computed in the time range \(t/\tilde{t}\in [0.0,18.0]\) where only minor damaged areas appear on the bed surface. Panels c and d provide the CDFs computed in the time range \(t/\tilde{t}\in [18.0,36.0]\) where highly damaged areas are observed (color figure online)

Full size image

In the initial stages of the process, \(t/\tilde{t}\in [0.0,18.0]\), the turbulent events producing a shear-stress leading to fracture are only \(9.0\%\) of the overall events. This value grows up to \(12.5\%\) in the following range of the simulated interval of time, \(t/\tilde{t}\in [18.0,36.0]\). For what concerns the wall-normal stresses, the turbulent events leading to a fracture are \(2.5\%\) in the first range of time and \(7.5\%\) in the latter one. These results confirm how the formation of irregular scour-structures on the fluid–solid interface enhances the fluid-induced stresses on the solid wall hence causing the acceleration of the erosion process described above.

5 Conclusions

The present paper addresses the direct numerical simulation of the erosion and evolution of the streambed morphology of an initially flattened bed of homogenous brittle material in a turbulent channel flow. Fluid-driven erosion is taken into account in an Eulerian-Lagrangian frame based on the coupling of peridynamics with the Navier–Stokes equations by means of the immersed boundary method. The proposed methodology, based on a non-local reformulation of solid mechanics, presents an intrinsic capability of realistically reproducing crack formation and branching in brittle materials. The focus of this paper is on the role of turbulence in promoting brittle fragmentation of the streambed and on the characterization of the interactions among bedforms and turbulent structures. We show how the erosion of the brittle streambed is activated by a fluid-driven fatigue mechanism. High-intensity turbulent events can enhance, temporarily and locally, the wall-stresses acting on the solid surface. Where the intensity of wall-stresses overcomes the ultimate stress of the brittle streambed, local damage is produced, and the formation of micro-cracks occurs. Local damages cause a reduction in the strength of the solid substrate facilitating the propagation of cracks by lower-intensity loads. By this fatigue mechanism, local damage accumulates over time, finally leading to the break up of the brittle substrate. This mechanism leads to the formation of irregular, shallow scour structures on the streambed. We observe a progressive deepening and widening of the scour resulting in long grooves extending in the streamwise direction. In turn, these formations are found to alter the structure of the flow, leading to an increment of the fluid stresses acting on the channel bed. At the smaller length scales, we put in relation this stress enhancement with the presence of small-scale coherent structures that persist over the bottom asperities generated by the scouring of the streambed. Similarly, we detect the formation of large-scale recirculating cells over the deeper scour-holes as well as turbulent stripes stationing along the grooves. Different statistics, based on average Eulerian quantities and Lagrangian observables are provided. In particular, the stress enhancement driven by the irregular pattern on the streambed can be detected in the probability density function of the wall stresses. The outcomes and data analysis of the simulation reported in his paper provide an insight into the fundamental mechanisms governing the erosion and bed morphology of submerged brittle sediments and their interaction with turbulent streams. The authors believe that the approach described in this paper will be useful for future investigations of fluid-driven erosion processes and their relation with turbulence in complex flows of environmental and engineering relevance.