Euler angles and numerical representation of the railroad track geometry

Abstract

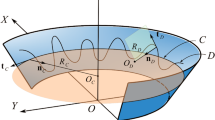
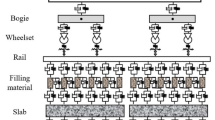
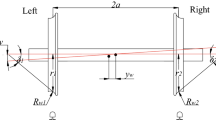
The geometry description plays a central role in many engineering applications and directly influences the quality of the computer simulation results. The geometry of a space curve can be completely defined in terms of two parameters: the horizontal and vertical curvatures, or equivalently, the curve curvature and torsion. In this paper, distinction is made between the track angle and space-curve bank angle, referred to in this paper as the Frenet bank angle. In railroad vehicle systems, the track bank angle measures the track super-elevation required to define a balance speed and achieve a safe vehicle operation. The formulation of the track space-curve differential equations in terms of Euler angles, however, shows the dependence of the Frenet bank angle on two independent parameters, often used as inputs in the definition of the track geometry. This paper develops the general differential equations that govern the track geometry using the Euler angle sequence adopted in practice. It is shown by an example that a curve can be twisted and vertically elevated but not super-elevated while maintaining a constant vertical-development angle. The continuity conditions at the track segment transitions are also examined. As discussed in the paper, imposing curvature continuity does not ensure continuity of the tangent vectors at the curve/spiral intersection. Several curve geometries that include planar and helix curves are used to explain some of the fundamental issues addressed in this study.

Appendix

1.1 Fresnel integrals

The Fresnel integrals S(x) and C(x) are defined by following power-series expansions which converge for all values of the argument x:

$$ \left. {\begin{array}{*{20}l} {S\left( x \right) = \int_{0}^{x} {\sin \left( {t^{2} } \right)} \,{\text{d}}t = \sum\limits_{n = 0}^{\infty } {\left( { - 1} \right)^{n} \frac{{x^{4n + 3} }}{{\left( {2n + 1} \right)!\left( {4n + 3} \right)}}} } \hfill \\ {C\left( x \right) = \int_{0}^{x} {\cos \left( {t^{2} } \right)} \,{\text{d}}t = \sum\limits_{n = 0}^{\infty } {\left( { - 1} \right)^{n} \frac{{x^{4n + 1} }}{{\left( {2n} \right)!\left( {4n + 1} \right)}}} } \hfill \\ \end{array} } \right\}. $$

(18)

The trace of the parametric plot of Fresnel integrals $\left[ {C(x),S(x)} \right]$ is called an Euler spiral or a clothoid, whose curvature at any point is proportional to the distance from the origin.