Skip to main content
SpringerLink
Log in

Static, stability and dynamic analyses of second strain gradient elastic Euler–Bernoulli beams

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

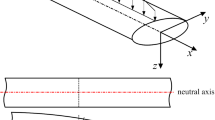
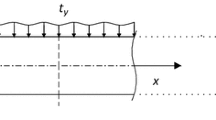
A simplified second strain gradient Euler–Bernoulli beam theory with two non-classical elastic coefficients in addition to the classical constants is presented. The governing equation and the associated classical and non-classical boundary conditions are derived with the aid of variational principles. The simplified second strain gradient theory is governed by an eighth-order differential equation with displacement, slope, curvature and triple derivative of displacement as degrees of freedom. This theory can be reduced to the first strain gradient and classical Euler–Bernoulli beam theories. Analytical solutions for static behaviour, free vibration and stability analyses are presented for different boundary conditions and length scale parameters. Using the numerical Laplace transform, a spectral element is developed for dynamic analysis of a cantilever beam subjected to a Gaussian pulse. Further, spectrum and dispersion relations are derived to study wave propagation characteristics. The gradient effects on the structural response are assessed and compared with the corresponding first strain gradient and classical beam theories. Observations show that the second strain gradient theory exhibiting stiffer behaviour in comparison to the first strain gradient and classical theories. The beam deflection decreases whereas frequencies and buckling load increase for increasing values of the gradient coefficient in comparison to the first strain gradient and classical theories. The forced response for a finite beam reveals a decrease in the amplitude and a shift to smaller time values with an increase in the value of length scale parameter. Additionally, the second strain gradient beam shows a dispersive behaviour, and for a given frequency the wavenumber decreases and the phase speed increases with an increase in the length scale parameter as compared to the first strain gradient beam theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Najar, F., Choura, S., El-Borgi, S., Abdel-Rahman, E.M., Nayfeh, A.H.: Modeling and design of variable-geometry electrostatic microactuators. J. Micromech. Microeng. 15, 419–429 (2005)

    Article  MATH  Google Scholar 

  2. Li, X., Bhushan, B., Takashima, K., Baek, C.W., Kim, Y.K.: Mechanical characterization of micro/nanoscale structures for MEMS/NEMS applications using nanoindentation techniques. Ultramicroscopy 97, 481–494 (2003)

    Article  Google Scholar 

  3. Lin, C.H., Ni, H., Wang, X., Chang, M., Chao, Y.J., Deka, J.R., Li, X.: In situ nanomechanical characterization of singlecrystalline boron nanowires by buckling. Small 6(8), 927–931 (2010)

    Article  Google Scholar 

  4. Zhu, Y., Qin, Q., Xu, F., Fan, F., Ding, Y., Zhang, T., Wang, Z.L.: Size effects on elasticity, yielding, and fracture of silver nanowires: In situ experiments. Phys. Rev. B 85(4), 045443 (2012)

    Article  Google Scholar 

  5. Jiang, W., Batra, R.: Molecular statics simulations of buckling and yielding of gold nanowires deformed in axial compression. Acta Materialia 57(16), 4921–4932 (2009)

    Article  Google Scholar 

  6. Wang, Z., Zu, X., Gao, F., Weber, W.J.: Atomistic simulations of the mechanical properties of silicon carbide nanowires. Phys. Rev. B 77(22), 224113 (2008)

    Article  Google Scholar 

  7. Rabkin, E., Nam, H.S., Srolovitz, D.: Atomistic simulation of the deformation of gold nanopillars. Acta Materialia 55(6), 2085–2099 (2007)

    Article  Google Scholar 

  8. Cosserat, E., Cosserat, F.: Theorie des corps deformables, Hermann Archives (reprint 2009)

  9. Eringen, A.C., Suhubi, E.S.: Nonlinear theory of simple microelastic solids, I and II, nonlinear theory of simple microelastic solids, I and II. Int. J. Eng. Sci. 2(189–203), 389–404 (1964)

    Google Scholar 

  10. Polizzotto, C.: Nonlocal elasticity and related variational principles. Int. J. Solids Struct. 38, 7359–7380 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  11. Eringen, A.C.: Nonlocal polar elastic continua. Int. J. Eng. Sci. 10, 1–16 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  12. Eringen, A.C.: On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 54, 4703–4710 (1983)

    Article  Google Scholar 

  13. Fleck, N.A., Hutchinson, J.W.: A phenomenological theory for strain gradient effects in plasticity. J. Mech. Phys. Solids 41(12), 1825–1857 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  14. Fleck, N.A., Hutchinson, J.W.: A reformulation of strain gradient plasticity. J. Mech. Phys. Solids 49, 2245–2271 (2001)

    Article  MATH  Google Scholar 

  15. Mindlin, R.D.: Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 16, 52–78 (1965)

    MathSciNet  Google Scholar 

  16. Mindlin, R.D., Eshel, N.: On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 4, 109–124 (1968)

    Article  MATH  Google Scholar 

  17. Toupin, R.: Elastic materials with couple-stresses. Arch. Ration. Mech Anal. 11, 385–414 (1962)

    Article  MathSciNet  MATH  Google Scholar 

  18. Koiter, W.T.: Couple-stresses in the theory of elasticity, I & II. Proc. K. Ned. Akad. Wet. (B) 67, 17–44 (1964)

    MathSciNet  MATH  Google Scholar 

  19. Askes, H., Aifantis, E.C.: Gradient elasticity in statics and dynamics: an overview of formulations, length scale identification procedures, finite element implementations and new results. Int. J. Solids Struct. 48, 1962–1990 (2011)

    Article  Google Scholar 

  20. Vardoulakis, I., Sulem, J.: Bifurcation Analysis in Geomechanics. Blackie/Chapman and Hall, London (1995)

    Google Scholar 

  21. Askes, H., Suiker, A.S.J., Sluys, L.J.: A classification of higher-order strain-gradient models linear analysis. Arch. Appl. Mech. 72, 171–188 (2002)

    Article  MATH  Google Scholar 

  22. Yang, F., Chong, A.C.M., Lam, D.C.C., Tong, P.: Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 51, 1477–1508 (2003)

    Article  MATH  Google Scholar 

  23. Lam, D.C.C., Yang, F., Chong, A.C.M., Wang, J., Tong, P.: Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 39, 2731–2743 (2002)

    Article  MATH  Google Scholar 

  24. Thai, H., Vo, T.P., Nguyen, T., Kim, S.: A review of continuum mechanics models for size-dependent analysis of beams and plates. Comput. Struct. 177(1), 196–219 (2017)

    Article  Google Scholar 

  25. Ma, H.M., Gao, X.L., Reddy, J.N.: A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. J. Mech. Phys. Solids. 56, 3379–3391 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  26. Akgoz, B., Civalek, O.: Analysis of micro-sized beams for various boundary conditions based on the strain gradient elasticity theory. Arch. Appl. Mech. 82(3), 423–43 (2012)

    Article  MATH  Google Scholar 

  27. Kong, S., Zhou, S., Nie, Z., Wang, K.: Static and dynamic analysis of micro beams based on strain gradient elasticity theory. Int. J. Eng. Sci. 47, 487–498 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  28. Reddy, J.N.: Nonlocal theories for bending, buckling, and vibration of beams. Int. J. Eng. Sci. 45, 288–307 (2007)

    Article  MATH  Google Scholar 

  29. Exadaktylos, G.E., Vardoulakis, I.: Microstructure in linear elasticity and scale effects: a reconsideration of basic rock mechanics and rock fracture mechanics. Tectonophysics 335, 81–109 (2001)

    Article  Google Scholar 

  30. Vardoulakis, I., Exadactylos, G., Kourkoulis, S.K.: Bending of marble with intrinsic length scales: a gradient theory with surface energy and size effects. J. Phys. IV. 8, 399–406 (1998)

    Google Scholar 

  31. Ru, C.Q., Aifantis, E.C.: A simple approach to solve boundary value problems in gradient elasticity. Acta Mech. 101, 59–68 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  32. Tsepoura, K.G., Papargyri-Beskou, S., Polyzos, D., Beskos, D.E.: Static and dynamic analysis of gradient elastic bars in tension. Arch. Appl. Mech. 72, 483–497 (2002)

    Article  MATH  Google Scholar 

  33. Georgiadis, H.G., Anagnostou, D.S.: Problems of Flamant-Boussinesq and Kelvin type in dipolar gradient elasticity. J. Elast. 90, 71–98 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  34. Gao, X.L., Ma, H.M.: Greens function and Eshelbys tensor based on a simplified strain gradient elasticity theory. Acta Mech. 207, 163–181 (2009)

    Article  Google Scholar 

  35. Georgiadis, H.G., Vardoulakis, I., Lykotrafitis, G.: Torsional surface waves in a gradient-elastic half-space. Wave Motion 31, 333–348 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  36. Georgiadis, H.G., Vardoulakis, I., Velgaki, E.G.: Dispersive Rayleigh-wave propagation in microstructured solids characterized by dipolar gradient elasticity. J. Elast. 74, 17–45 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  37. Polyzos, D., Fotiadis, D.I.: Derivation of Mindlins gradient elastic theory via simple lattice and continuum models. Int. J. Solids Struct. 49, 470–480 (2012)

    Article  Google Scholar 

  38. Papargyri-Beskou, S., Tsepoura, K.G., Polyzos, D., Beskos, D.E.: Bending and stability analysis of gradient elastic beams. Int. J. Solids Struct. 40, 385–400 (2003)

    Article  MATH  Google Scholar 

  39. Papargyri-Beskou, S., Polyzos, D., Beskos, D.E.: Dynamic analysis of gradient elastic flexural beams. Struct. Eng. Mech. 15(6), 705–716 (2003)

    Article  MATH  Google Scholar 

  40. Lazopoulos, A.K.: Dynamic response of thin strain gradient elastic beams. Int. J. Mech. Sci. 58, 27–33 (2012)

    Article  Google Scholar 

  41. Lazopoulos, K.A., Lazopoulos, A.K.: Bending and buckling of thin strain gradient elastic beams. Eur. J. Mech. A/Solids 29, 837–843 (2010)

    Article  Google Scholar 

  42. Pegios, I.P., Papargyri-Beskou, S., Beskos, D.E.: Finite element static and stability analysis of gradient elastic beam structures. Acta Mech. 226, 745–768 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  43. Pegios, I.P., Hatzigeorgiou, G.D.: Finite element free and forced vibration analysis of gradient elastic beam structures. Acta Mech. 229, 4817–4830 (2018)

    Article  MathSciNet  Google Scholar 

  44. Tsinopoulos, S.V., Polyzos, D., Beskos, D.E.: Static and dynamic BEM analysis of strain gradient elastic solids and structures. Comput. Mod. Eng. Sci. 86, 113–144 (2012)

    MathSciNet  MATH  Google Scholar 

  45. Mindlin, R.D.: Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1, 417–438 (1965)

    Article  Google Scholar 

  46. Chien, HWu: Cohesive elasticity and surface phenomena. Q. Appl. Math. 1, 73–103 (1992)

    MathSciNet  MATH  Google Scholar 

  47. Amiot, F.: An EulerBernoulli second strain gradient beam theory for cantilever sensors. Philos. Mag. Lett. 93(4), 204–212 (2013)

    Article  Google Scholar 

  48. Shodja, H.M., Ahmadpoor, F., Tehranchi, A.: Calculation of the additional constants for FCC materials in second strain gradient elasticity: behavior of a nano-size Bernoulli–Euler beam with surface effects. J. Appl. Mech. 79, 021008 (2012)

    Article  Google Scholar 

  49. Ojaghnezhad, F., Shodja, H.M.: A combined first principles and analytical determination of the modulus of cohesion, surface energy and the additional constants in the second strain gradient elasticity. Int. J. Solids Struct. 50, 3967–3974 (2013)

    Article  Google Scholar 

  50. Cordero, N.M., Forest, S., Busso, E.P.: Second strain gradient elasticity of nano-objects. J. Mech. Phys. Solids 97, 92–124 (2016)

    Article  MathSciNet  Google Scholar 

  51. Polyzos, D., Fotiadis, D.I.: Derivation of Mindlins first and second strain gradient elastic theory via simple lattice and continuum models. Int. J. Solids Struct. 49, 470–480 (2012)

    Article  Google Scholar 

  52. Polizzotto, C.: A gradient elasticity theory for second-grade materials and higher order inertia. Int. J. Solids Struct. 49, 2121–2137 (2012)

    Article  Google Scholar 

  53. Polizzotto, C.: A second strain gradient elasticity theory with second velocity gradient inertia Part I: constitutive equations and quasi-static behavior. Int. J. Solids Struct. 50, 3749–3765 (2013)

    Article  Google Scholar 

  54. Polizzotto, C.: A second strain gradient elasticity theory with second velocity gradient inertia Part II: dynamic behaviour. Int. J. Solids Struct. 50, 3766–3777 (2013)

    Article  Google Scholar 

  55. Forest, S., Cordero, N.M., Busso, E.P.: First vs. second gradient of strain theory for capillarity effects in an elastic fluid at small length scales. Comput. Mater. Sci. 50, 1299–1304 (2011)

    Article  Google Scholar 

  56. Momeni, S.A., Asghari, M.: The second strain gradient functionally graded beam formulation. Comput. Struct. 188, 15–24 (2018)

    Article  Google Scholar 

  57. Lazar, M., Maugin, G.A., Aifantis, E.C.: Dislocations in second strain gradient elasticity. Int. J. Solids Struct. 43, 1787–1817 (2006)

    Article  MATH  Google Scholar 

  58. Polizzotto, C.: Gradient elasticity and non standard boundary conditions. Int. J. Solids Struct. 40, 7399–7423 (2003)

    Article  MATH  Google Scholar 

  59. Deng, S., Liu, J., Liang, N.: Wedge and twist disclinations in second strain gradient elasticity. Int. J. Solids Struct. 44, 3646–3665 (2007)

    Article  MATH  Google Scholar 

  60. Polizzotto, C.: Surface effects, boundary conditions and evolution laws within second strain gradient plasticity. Int. J. Plast. 60, 197–216 (2014)

    Article  Google Scholar 

  61. Zhang, X., Jiao, K., Sharma, P., Yakobson, B.I.: An atomistic and non-classical continuum field theoretic perspective of elastic interactions between defects (force dipole) of various symmetries and application to graphene. J. Mech. Phys. Solids. 54, 2304–2329 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  62. Lazar, M.: The fundamentals of nano-singular dislocations in the theory of gradient elasticity: dislocation loops and straight dislocations. Int. J. Solids Struct. 50, 352–362 (2013)

    Article  Google Scholar 

  63. Ishaquddin, Md., Gopalakrishnan, S.: Differential quadrature element for second strain gradient beam theory. arXiv:1807.08622 (2016)

  64. Ishaquddin, Md., Gopalakrishnan, S.: Novel weak form quadrature elements for second strain gradient Euler–Bernoulli beam theory. arXiv:1807.08625 (2016)

  65. Ramirez, A., Gomez, P., Moreno, P., Gutierrez, A.: Frequency domain analysis of electromagnetic transients through the numerical Laplace transforms. In: Proceedings of IEEE Power Engineering Society of America, Denver, CO, USA, vol. 1, pp. 1136–1139 (2004)

  66. Moreno, P., Ramirez, A.: Implementation of numerical Laplace transform: a review. IEEE Trans. Power Deliv. 23(4), 2599–2609 (2008)

    Article  Google Scholar 

  67. Igawa, H., Komatsu, K., Yamaguchi, I., Kasai, T.: Wave propagation analysis of frame structures using the spectral element method. J. Sound Vib. 277, 1071–1081 (2003)

    Article  Google Scholar 

  68. Blais, J.F., Cimmino, M., Ross, A., Granger, D.: Suppression of time aliasing in the solution of the equations of motion of an impacted beam with partial constrained layer damping. J. Sound Vib. 326, 870–882 (2009)

    Article  Google Scholar 

  69. Kishor, D.K., Gopalakrishnan, S., Ganguli, R.: Three-dimensional sloshing: A consistent finite element approach. Int. J. Numer. Methods Fluids. 66(3), 345–376 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  70. Doyle, J.F., Farris, T.N.: A spectrally formulated finite element for flexural wave propagation in beams. Int. J. Anal. Exp. Modal Anal. 5, 13–23 (1990)

    Google Scholar 

  71. Doyle, J.F.: Wave Propagation in Structures, 2nd edn. Springer, New York (1997)

    Book  MATH  Google Scholar 

  72. Gopalakrishnan, S., Chakraborty, A., Mahapatra, D.R.: Spectral Finite Element Method. Springer, London (2008)

    MATH  Google Scholar 

  73. Wilcox, D.J.: Numerical Laplace transformation and inversion. Int. J. Electr. Eng. Educ. 15(3), 247–265 (1978)

    Article  Google Scholar 

  74. Wedepohl, L.M.: Power systems transients: errors incurred in the numerical inversion of the Laplace transform. In: Proceedings of Midwest Symposium on Circuits and Systems, Puebla, Mex, pp. 174–178 (1983)

  75. Murthy, M.V.V.S., Gopalakrishnan, S., Nair, P.S.: Signal wrap-around free spectral element formulation for multiply connected finite 1D waveguides. J. Aerosp. Sci. Technol. 63(1), 72–88 (2011)

    Google Scholar 

  76. Patra, A.K., Gopalakrishnan, S., Ganguli, R.: A spectral multiscale method for wave propagation analysis: atomistic continuum coupled simulation. Comput. Methods Appl. Mech. Eng. 278, 744–764 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  77. Gopalakrishnan, S.: Wave Propagation in Materials and Structures. Taylor & Francis Group/CRC Press, New York (2017)

    MATH  Google Scholar 

  78. Cooley, J.W., Tukey, O.W.: An algorithm for the machine clculation of complex Fourier series. Math. Comput. 19(90), 297–301 (1965)

    Article  MATH  Google Scholar 

  79. Cooley, J.W., Lewis, P.A.W., Welch, P.D.: The fast Fourier transform algorithm: programming considerations in the calculation of sine, cosine and laplace transforms. J. Sound Vib. 12, 315–337 (1970)

    Article  MATH  Google Scholar 

  80. Kitahara, M.: Boundary Integral Equation Methods in Eigenvalue Problems of Elastodynamics and Thin Plates. Elsevier, Amsterdam (1985)

    MATH  Google Scholar 

  81. Reddy, J.N.: Energy Principles and Variational Methods in Applied Mechanics, 2nd edn. Wiley, New York (2002)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Aerospace Engineering, Indian Institute of Science, Bengaluru, 560012, India

    Md. Ishaquddin & S. Gopalakrishnan

Authors
  1. Md. Ishaquddin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Gopalakrishnan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Md. Ishaquddin.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

1.1 A. Stiffness matrix and force vector for static analysis of second strain gradient Euler–Bernoulli beam

The following is the list of stiffness matrices and load vectors for different boundary conditions:

(a) Simply supported beam:

$$\begin{aligned}{}[K]= \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1\\ 1 &{} L &{} L^2 &{} L^3 &{} e^{m_{1}L} &{} e^{m_{2}L} &{} e{n_{1}L} &{} e^{n_{2}L}\\ 0 &{} 0 &{} 2 &{} 0 &{} a_{11} &{} a_{12} &{} a_{13} &{} a_{14}\\ 0 &{} 0 &{} 2 &{} 6L &{} b_{11} &{} b_{12} &{} b_{13} &{} b_{14}\\ 0 &{} 0 &{} 2 &{} 0 &{} m_{1}^{2} &{} m_{2}^{2} &{} n_{1}^{2} &{} n_{2}^{2} \\ 0 &{} 0 &{} 2 &{} 6L &{} m_{1}^{2}e^{m_{1}L} &{} m_{2}^{2}e^{m_{2}L} &{} n_{1}^{2}e^{n_{1}L} &{} n_{2}^{2}e^{n_{2}L}\\ 0 &{} 0 &{} 0 &{} 6 &{} m_{1}^{3} &{} m_{2}^{3} &{} n_{1}^{3} &{} n_{2}^{3}\\ 0 &{} 0 &{} 0 &{} 6 &{} m_{1}^{3}e^{m_{1}L} &{} m_{2}^{3}e^{m_{2}L} &{} n_{1}^{3}e^{n_{1}L} &{} n_{2}^{3}e^{n_{2}L}\\ \end{bmatrix}, \quad \{f\}=\begin{Bmatrix} 0 \\ -qL^{4}/24EI \\ g_{1}^{2}q/EI\\ g_{1}^{2}q/EI-qL^{2}/2EI\\ 0 \\ -qL^{2}/2EI\\ 0\\ -qL/EI\\ \end{Bmatrix}, \end{aligned}$$
(A.1)

where

$$\begin{aligned}&a_{11}= m_{1}^{2}-g_{1}^{2}m_{1}^{4}+g_{2}^{4}m_{1}^{6},\quad\quad \quad a_{12}= m_{2}^{2}-g_{1}^{2}m_{2}^{4}+g_{2}^{4}m_{2}^{6},\\&a_{13}=n_{1}^{2}-g_{1}^{2}n_{1}^{4}+g_{2}^{4}n_{1}^{6}\, , \quad \quad \quad \, a_{14}= n_{2}^{2}-g_{1}^{2}n_{2}^{4}+g_{2}^{4}n_{2}^{6},\\&b_{11}= (m_{1}^{2}-g_{1}^{2}m_{1}^{4}+g_{2}^{4}m_{1}^{6})e^{m_{1}L},\quad b_{12}= (m_{2}^{2}-g_{1}^{2}m_{2}^{4}+g_{2}^{4}m_{2}^{6})e^{m_{2}L},\\&b_{13}= (n_{1}^{2}-g_{1}^{2}n_{1}^{4}+g_{2}^{4}n_{1}^{6})e^{n_{1}L},\quad \,b_{14}= (n_{2}^{2}-g_{1}^{2}n_{2}^{4}+g_{2}^{4}n_{2}^{6})e^{n_{2}L}. \end{aligned}$$

(b) Cantilever beam:

$$\begin{aligned}{}[K]= \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1\\ 0 &{} 0 &{} 0 &{} 6 &{} a_{21} &{}a_{22} &{} a_{23} &{}a_{24}\\ 0 &{} 1 &{} 0 &{} 0 &{} m_{1} &{} m_{2} &{} n_{1} &{} n_{2}\\ 0 &{} 0 &{} 2 &{} 6L &{} b_{11} &{} b_{12} &{} b_{13} &{} b_{14}\\ 0 &{} 0 &{} 2 &{} 0 &{} m_{1}^{2} &{} m_{2}^{2} &{} n_{1}^{2} &{} n_{2}^{2} \\ 0 &{} 0 &{} 0 &{} 6g_{1}^{2} &{} b_{21} &{} b_{22} &{} b_{23} &{} b_{24}\\ 0 &{} 0 &{} 0 &{} 6 &{} m_{1}^{3} &{} m_{2}^{3} &{} n_{1}^{3} &{} n_{2}^{3}\\ 0 &{} 0 &{} 0 &{} 0 &{} c_{11} &{} c_{12} &{} c_{13} &{} c_{14}\\ \end{bmatrix}, \quad \{f\}=\begin{Bmatrix} 0 \\ -qL/EI \\ 0\\ g_{1}^{2}q/EI-qL^{2}/2EI\\ 0\\ -g_{1}^{2}Lq/EI\\ 0\\ 0\\ \end{Bmatrix} ,\end{aligned}$$
(A.2)

where

$$\begin{aligned}&a_{21}=(m_{1}^{3}-g_{1}^{2}m_{1}^{5}+g_{2}^{4}m_{1}^{7})e^{m_{1}L},\quad a_{22}=(m_{2}^{3}-g_{1}^{2}m_{2}^{5}+g_{2}^{4}m_{2}^{7})e^{m_{2}L},\\&a_{23}=(n_{1}^{3}-g_{1}^{2}n_{1}^{5}+g_{2}^{4}n_{1}^{7})e^{n_{1}L},\quad \quad a_{24}=(n_{2}^{3}-g_{1}^{2}n_{2}^{5}+g_{2}^{4}n_{2}^{7})e^{n_{2}L},\\ \end{aligned}$$
$$\begin{aligned}&b_{21}=(g_{1}^{2}m_{1}^{3}-g_{2}^{4}m_{1}^{5})e^{m_{1}L},\quad b_{22}=(g_{1}^{2}m_{2}^{3}-g_{2}^{4}m_{2}^{5})e^{m_{2}L},\\&b_{23}=(g_{1}^{2}n_{1}^{3}-g_{2}^{4}n_{1}^{5})e^{n_{1}L},\quad \quad b_{24}=(g_{1}^{2}n_{2}^{3}-g_{2}^{4}n_{2}^{5})e^{n_{2}L}\\ \end{aligned}$$
$$\begin{aligned}&c_{11}=g_{2}^{4}m_{1}^{4}e^{m_{1}L},\quad c_{12}=g_{2}^{4}m_{2}^{4}e^{m_{2}L},\quad c_{13}=g_{2}^{4}n_{1}^{4}e^{n_{1}L},\quad c_{14}=g_{2}^{4}n_{2}^{4}e^{n_{2}L},\\&h_{21}=(m_{1}^{2}-g_{1}^{2}m_{1}^{4}+g_{2}^{4}m_{1}^{6})e^{m_{1}L},\quad h_{22}=(m_{2}^{2}-g_{1}^{2}m_{2}^{4}+g_{2}^{4}m_{2}^{6})e^{m_{2}L},\\&h_{23}=(n_{1}^{2}-g_{1}^{2}n_{1}^{4}+g_{2}^{4}n_{1}^{6})e^{n_{1}L},\quad \quad h_{24}=(n_{2}^{2}-g_{1}^{2}n_{2}^{4}+g_{2}^{4}n_{2}^{6})e^{n_{2}L}.\\ \end{aligned}$$

(c) Clamped beam:

$$\begin{aligned}{}[K]= \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1\\ 1 &{} L &{} L^{2} &{} L^{3} &{} e^{m_{1}L} &{} e^{m_{2}L} &{} e^{n_{1}L} &{}e^{n_{2}L}\\ 0 &{} 1 &{} 0 &{} 0 &{} m_{1} &{} m_{2} &{} n_{1} &{} n_{2} \\ 0 &{} 1 &{} 2L &{} 3L^{2} &{} m_{1}e^{m_{1}L} &{} m_{2}e^{m_{2}L} &{} n_{1}e^{n_{1}L} &{} n_{2}e^{n_{2}L}\\ 0 &{} 0 &{} 2 &{} 0 &{} m_{1}^{2} &{} m_{2}^{2} &{} n_{1}^{2} &{} n_{2}^{2} \\ 0 &{} 0 &{} 2 &{} 6L &{} m_{1}^{2}e^{m_{1}L} &{} m_{2}^{2}e^{m_{2}L} &{} n_{1}^{2}e^{n_{1}L} &{} n_{2}^{2}e^{n_{2}L}\\ 0 &{} 0 &{} 0 &{} 6 &{} m_{1}^{3} &{} m_{2}^{3} &{} n_{1}^{3} &{} n_{2}^{3} \\ 0 &{} 0 &{} 0 &{} 6 &{} m_{1}^{3}e^{m_{1}L} &{} m_{3}^{2}e^{m_{2}L} &{} n_{1}^{3}e^{n_{1}L} &{} n_{2}^{3}e^{n_{2}L}\\ \end{bmatrix}, \quad \{f\}=\begin{Bmatrix} 0 \\ -qL^{4}/24EI \\ 0\\ -qL^{3}/6EI \\ 0\\ -qL^{2}/2EI\\ 0\\ -qL/EI\\ \end{Bmatrix} \end{aligned}$$
(A.3)

1.2 B. Frequency equations for free vibration analysis of second strain gradient Euler–Bernoulli beam

The following are the frequency equations for different boundary conditions:

(a) Simply supported beam:

$$\begin{aligned}{}[F(\omega )]=\begin{bmatrix} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1&{} 1 &{} 1\\ {e}^{({\alpha }_{1}L)} &{} {e}^{({\alpha }_{2}L)} &{} {e}^{({\alpha }_{3}L)} &{} {e}^{({\alpha }_{4}L)} &{} {e}^{({\alpha }_{5}L)} &{} {e}^{({\alpha }_{6}L)}&{} {e}^{({\alpha }_{7}L)} &{} {e}^{({\alpha }_{8}L)} \\ {{\alpha }_{1}}^2 &{} {{\alpha }_{2}}^2 &{} {{\alpha }_{3}}^2 &{} {{\alpha }_{4}}^2 &{} {{\alpha }_{5}}^2 &{} {{\alpha }_{6}}^2&{} {{\alpha }_{7}}^2 &{} {{\alpha }_{8}}^2\\ t_{1} &{}t_{2}&{}t_{3}&{}t_{4}&{}t_{5}&{}t_{6}&{}t_{7}&{}t_{8}\\ t_{1}{e}^{({\alpha }_{1}L)} &{}t_{2}{e}^{({\alpha }_{2}L)}&{}t_{3}{e}^{({\alpha }_{3}L)}&{}t_{4}{e}^{({\alpha }_{4}L)}&{}t_{5}{e}^{({\alpha }_{5}L)}&{}t_{6}{e}^{({\alpha }_{6}L)}&{}t_{7}{e}^{({\alpha }_{7}L)}&{}t_{8}{e}^{({\alpha }_{8}L)}\\ {\alpha }_{1}^{3} &{} {\alpha }_{2}^{3} &{} {\alpha }_{3}^{3} &{} {\alpha }_{4}^{3} &{} {\alpha }_{5}^{3} &{} {\alpha }_{6}^{3}&{} {\alpha }_{7}^{3} &{} {\alpha }_{8}^{3} \\ {\alpha }_{1}^{3}{e}^{({\alpha }_{1}L)} &{} {\alpha }_{2}^{3}{e}^{({\alpha }_{2}L)} &{} {\alpha }_{3}^{3}{e}^{({\alpha }_{3}L)} &{} {\alpha }_{4}^{3}{e}^{({\alpha }_{4}L)} &{} {\alpha }_{5}^{3}{e}^{({\alpha }_{5}L)} &{} {\alpha }_{6}^{3}{e}^{({\alpha }_{6}L)} &{} {\alpha }_{7}^{3}{e}^{({\alpha }_{7}L)} &{} {\alpha }_{8}^{3}{e}^{({\alpha }_{8}L)}\\ \end{bmatrix} \end{aligned}$$
(B.1)

(b) Cantilever beam:

$$\begin{aligned}{}[F(\omega )]=\begin{bmatrix} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1&{} 1 &{} 1\\ {{\alpha }_{1}} &{} {{\alpha }_{2}} &{} {{\alpha }_{3}} &{} {{\alpha }_{4}} &{} {{\alpha }_{5}} &{} {{\alpha }_{6}}&{} {{\alpha }_{7}} &{} {{\alpha }_{8}}\\ {{\alpha }_{1}}^2 &{} {{\alpha }_{2}}^2 &{} {{\alpha }_{3}}^2 &{} {{\alpha }_{4}}^2 &{} {{\alpha }_{5}}^2 &{} {{\alpha }_{6}}^2&{} {{\alpha }_{7}}^2 &{} {{\alpha }_{8}}^2\\ {{\alpha }_{1}}^3 &{} {{\alpha }_{2}}^3 &{} {{\alpha }_{3}}^3 &{} {{\alpha }_{4}}^3 &{} {{\alpha }_{5}}^3 &{} {{\alpha }_{6}}^3&{} {{\alpha }_{7}}^3 &{} {{\alpha }_{8}}^3\\ p_{1}{e}^{({\alpha }_{1}L)} &{}p_{2}{e}^{({\alpha }_{2}L)}&{}p_{3}{e}^{({\alpha }_{3}L)}&{}p_{4}{e}^{({\alpha }_{4}L)}&{}p_{5}{e}^{({\alpha }_{5}L)}&{}p_{6}{e}^{({\alpha }_{6}L)}&{}p_{7}{e}^{({\alpha }_{7}L)}&{}p_{8}{e}^{({\alpha }_{8}L)}\\ r_{1}{e}^{({\alpha }_{1}L)} &{}r_{2}{e}^{({\alpha }_{2}L)}&{}r_{3}{e}^{({\alpha }_{3}L)}&{}r_{4}{e}^{({\alpha }_{4}L)}&{}r_{5}{e}^{({\alpha }_{5}L)}&{}r_{6}{e}^{({\alpha }_{6}L)}&{}r_{7}{e}^{({\alpha }_{7}L)}&{}r_{8}{e}^{({\alpha }_{8}L)}\\ q_{1}{e}^{({\alpha }_{1}L)} &{}q_{2}{e}^{({\alpha }_{2}L)}&{}q_{3}{e}^{({\alpha }_{3}L)}&{}q_{4}{e}^{({\alpha }_{4}L)}&{}q_{5}{e}^{({\alpha }_{5}L)}&{}q_{6}{e}^{({\alpha }_{6}L)}&{}q_{7}{e}^{({\alpha }_{7}L)}&{}q_{8}{e}^{({\alpha }_{8}L)}\\ {\alpha }_{1}^{4}{e}^{({\alpha }_{1}L)} &{} {\alpha }_{2}^{4}{e}^{({\alpha }_{2}L)} &{} {\alpha }_{3}^{4}{e}^{({\alpha }_{3}L)} &{} {\alpha }_{4}^{4}{e}^{({\alpha }_{4}L)} &{} {\alpha }_{5}^{4}{e}^{({\alpha }_{5}L)} &{} {\alpha }_{6}^{4}{e}^{({\alpha }_{6}L)} &{} {\alpha }_{7}^{4}{e}^{({\alpha }_{7}L)} &{} {\alpha }_{8}^{4}{e}^{({\alpha }_{8}L)}\\ \end{bmatrix} \end{aligned}$$
(B.2)

(c) Clamped beam:

$$\begin{aligned}{}[F(\omega )]=\begin{bmatrix} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1&{} 1 &{} 1\\ {e}^{({\alpha }_{1}L)} &{} {e}^{({\alpha }_{2}L)} &{} {e}^{({\alpha }_{3}L)} &{} {e}^{({\alpha }_{4}L)} &{} {e}^{({\alpha }_{5}L)} &{} {e}^{({\alpha }_{6}L)}&{} {e}^{({\alpha }_{7}L)} &{} {e}^{({\alpha }_{8}L)} \\ {{\alpha }_{1}} &{} {{\alpha }_{2}} &{} {{\alpha }_{3}} &{} {{\alpha }_{4}} &{} {{\alpha }_{5}} &{} {{\alpha }_{6}}&{} {{\alpha }_{7}} &{} {{\alpha }_{8}}\\ {{\alpha }_{1}}{e}^{({\alpha }_{1}L)} &{} {{\alpha }_{2}}{e}^{({\alpha }_{2}L)} &{} {{\alpha }_{3}}{e}^{({\alpha }_{3}L)} &{} {{\alpha }_{4}}{e}^{({\alpha }_{4}L)} &{} {{\alpha }_{5}}{e}^{({\alpha }_{5}L)} &{} {{\alpha }_{6}}{e}^{({\alpha }_{6}L)}&{} {{\alpha }_{7}}{e}^{({\alpha }_{7}L)} &{} {{\alpha }_{8}}{e}^{({\alpha }_{8}L)} \\ {{\alpha }_{1}}^2 &{} {{\alpha }_{2}}^2 &{} {{\alpha }_{3}}^2 &{} {{\alpha }_{4}}^2 &{} {{\alpha }_{5}}^2 &{} {{\alpha }_{6}}^2&{} {{\alpha }_{7}}^2 &{} {{\alpha }_{8}}^2\\ {\alpha }_{1}^{2}{e}^{({\alpha }_{1}L)} &{} {\alpha }_{2}^{2}{e}^{({\alpha }_{2}L)} &{} {\alpha }_{3}^{2}{e}^{({\alpha }_{3}L)} &{} {\alpha }_{4}^{2}{e}^{({\alpha }_{4}L)} &{} {\alpha }_{5}^{2}{e}^{({\alpha }_{5}L)} &{} {\alpha }_{6}^{2}{e}^{({\alpha }_{6}L)} &{} {\alpha }_{7}^{2}{e}^{({\alpha }_{7}L)} &{} {\alpha }_{8}^{2}{e}^{({\alpha }_{8}L)}\\ {{\alpha }_{1}}^3 &{} {{\alpha }_{2}}^3 &{} {{\alpha }_{3}}^3 &{} {{\alpha }_{4}}^3 &{} {{\alpha }_{5}}^3 &{} {{\alpha }_{6}}^3&{} {{\alpha }_{7}}^3 &{} {{\alpha }_{8}}^3\\ {\alpha }_{1}^{3}{e}^{({\alpha }_{1}L)} &{} {\alpha }_{2}^{3}{e}^{({\alpha }_{2}L)} &{} {\alpha }_{3}^{3}{e}^{({\alpha }_{3}L)} &{} {\alpha }_{4}^{3}{e}^{({\alpha }_{4}L)} &{} {\alpha }_{5}^{3}{e}^{({\alpha }_{5}L)} &{} {\alpha }_{6}^{3}{e}^{({\alpha }_{6}L)} &{} {\alpha }_{7}^{3}{e}^{({\alpha }_{7}L)} &{} {\alpha }_{8}^{3}{e}^{({\alpha }_{8}L)}\\ \end{bmatrix} ,\end{aligned}$$
(B.3)

where

$$\begin{aligned} t_{1}&= {} (-g_{1}^{2}{\alpha }_{1}^{4}+g_{2}^{4}{\alpha }_{1}^{6}),\quad t_{2}=(-g_{1}^{2}{\alpha }_{2}^{4}+g_{2}^{4}{\alpha }_{2}^{6}) ,\quad t_{3}=(-g_{1}^{2}{\alpha }_{3}^{4}+g_{2}^{4}{\alpha }_{3}^{6}),\\ t_{4}&= {} (-g_{1}^{2}{\alpha }_{4}^{4}+g_{2}^{4}{\alpha }_{4}^{6}) ,\quad t_{5}=(-g_{1}^{2}{\alpha }_{5}^{4}+g_{2}^{4}{\alpha }_{5}^{6}), \quad t_{6}=(-g_{1}^{2}{\alpha }_{6}^{4}+g_{2}^{4}{\alpha }_{6}^{6}),\\ t_{7}&= {} (-g_{1}^{2}{\alpha }_{7}^{4}+g_{2}^{4}{\alpha }_{7}^{6}) ,\quad t_{8}=(-g_{1}^{2}{\alpha }_{8}^{4}+g_{2}^{4}{\alpha }_{8}^{6}) ,\end{aligned}$$
$$\begin{aligned} p_{1}&= {} ({\alpha }_{1}^{3}-g_{1}^{2}{{\alpha }_{1}}^{5}+g_{2}^{4}{{\alpha }_{1}}^{7}), \quad p_{2}=({\alpha }_{2}^{3}-g_{1}^{2}{{\alpha }_{2}}^{5}+g_{2}^{4}{{\alpha }_{2}}^{7}),\\ p_{3}&= {} ({\alpha }_{3}^{3}-g_{1}^{2}{{\alpha }_{3}}^{5}+g_{2}^{4}{{\alpha }_{3}}^{7}), \quad p_{4}=({\alpha }_{4}^{3}-g_{1}^{2}{{\alpha }_{4}}^{5}+g_{2}^{4}{{\alpha }_{4}}^{7}),\\ p_{5}&= {} ({\alpha }_{5}^{3}-g_{1}^{2}{{\alpha }_{5}}^{5}+g_{2}^{4}{{\alpha }_{5}}^{7}), \quad p_{6}=({\alpha }_{6}^{3}-g_{1}^{2}{{\alpha }_{6}}^{5}+g_{2}^{4}{{\alpha }_{6}}^{7}),\\ p_{7}&= {} ({\alpha }_{7}^{3}-g_{1}^{2}{{\alpha }_{7}}^{5}+g_{2}^{4}{{\alpha }_{7}}^{7}), \quad p_{8}=({\alpha }_{8}^{3}-g_{1}^{2}{{\alpha }_{8}}^{5}+g_{2}^{4}{{\alpha }_{8}}^{7}).\\ \end{aligned}$$
$$\begin{aligned} r_{1}&= {} ({\alpha }_{1}^{2}-g_{1}^{2}{{\alpha }_{1}}^{4}+g_{2}^{4}{{\alpha }_{1}}^{6}) ,\quad r_{2}=({\alpha }_{2}^{2}-g_{1}^{2}{{\alpha }_{2}}^{4}+g_{2}^{4}{{\alpha }_{2}}^{6}),\\ r_{3}&= {} ({\alpha }_{3}^{2}-g_{1}^{2}{{\alpha }_{3}}^{4}+g_{2}^{4}{{\alpha }_{3}}^{6}) ,\quad r_{4}=({\alpha }_{4}^{2}-g_{1}^{2}{{\alpha }_{4}}^{4}+g_{2}^{4}{{\alpha }_{4}}^{6}), \\ r_{5}&= {} ({\alpha }_{5}^{2}-g_{1}^{2}{{\alpha }_{5}}^{4}+g_{2}^{4}{{\alpha }_{5}}^{6}), \quad r_{6}=(k_{6}^{2}-g_{1}^{2}{{\alpha }_{6}}^{4}+g_{2}^{4}{{\alpha }_{6}}^{6}), \\ r_{7}&= {} ({\alpha }_{7}^{2}-g_{1}^{2}{{\alpha }_{7}}^{4}+g_{2}^{4}{{\alpha }_{7}}^{6}), \quad r_{8}=({\alpha }_{8}^{2}-g_{1}^{2}{{\alpha }_{8}}^{4}+g_{2}^{4}{{\alpha }_{8}}^{6}), \end{aligned}$$
$$\begin{aligned} q_{1}&= {} (g_{1}^{2}{{\alpha }_{1}}^{3}-g_{2}^{4}{{\alpha }_{1}}^{5}) ,\quad q_{2}=(g_{1}^{2}{{\alpha }_{2}}^{3}-g_{2}^{4}{{\alpha }_{2}}^{5}), \\ q_{3}&= {} (g_{1}^{2}{{\alpha }_{3}}^{3}-g_{2}^{4}{{\alpha }_{3}}^{5}) ,\quad q_{4}=(g_{1}^{2}{{\alpha }_{4}}^{3}-g_{2}^{4}{{\alpha }_{4}}^{5}) ,\\ q_{5}&= {} (g_{1}^{2}{{\alpha }_{5}}^{3}-g_{2}^{4}{{\alpha }_{5}}^{5}), \quad q_{6}=(g_{1}^{2}{{\alpha }_{6}}^{3}-g_{2}^{4}{{\alpha }_{6}}^{5}) ,\\ q_{7}&= {} (g_{1}^{2}{{\alpha }_{7}}^{3}-g_{2}^{4}{{\alpha }_{7}}^{5}), \quad q_{8}=(g_{1}^{2}{{\alpha }_{8}}^{3}-g_{2}^{4}{{\alpha }_{8}}^{5}) ,\end{aligned}$$

1.3 C. Geometric stiffness matrix for buckling analysis of second strain gradient Euler–Bernoulli beam

The following are the geometric stiffness matrices for different boundary conditions:

(a) Simply supported beam:

$$\begin{aligned}{}[G(P)]= \begin{bmatrix} 1 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1&{} 1 &{} 1\\ 1 &{} L &{} {e}^{(m_{1}L)} &{} {e}^{(m_{2}L)} &{} {e}^{(m_{3}L)} &{} {e}^{(n_{1}L)}&{} {e}^{(n_{2}L)} &{} {e}^{(n_{3}L)} \\ 0 &{} 0 &{} {m_{1}}^2 &{} {m_{2}}^2 &{} {m_{3}}^2 &{} {n_{1}}^2&{} {n_{2}}^2 &{} {n_{3}}^2\\ 0 &{} 0 &{} t_{3}&{}t_{4}&{}t_{5}&{}t_{6}&{}t_{7}&{}t_{8}\\ 0 &{} 0 &{} t_{3}{e}^{(m_{1}L)}&{}t_{4}{e}^{(m_{2}L)}&{}t_{5}{e}^{(m_{3}L)}&{}t_{6}{e}^{(n_{1}L)}&{}t_{7}{e}^{(n_{2}L)}&{}t_{8}{e}^{(n_{3}L)}\\ 0 &{} 0 &{} m_{1}^{3} &{} m_{2}^{3} &{} m_{3}^{3} &{} n_{1}^{3}&{} n_{2}^{3} &{} n_{3}^{3} \\ 0 &{} 0 &{} m_{1}^{3}{e}^{(m_{1}L)} &{} m_{2}^{3}{e}^{(m_{2}L)} &{} n_{1}^{3}{e}^{(n_{1}L)} &{} n_{2}^{3}{e}^{(n_{2}L)} &{} n_{3}^{3}{e}^{(n_{3}L)} &{} n_{4}^{3}{e}^{(n_{4}L)}\\ \end{bmatrix} \end{aligned}$$
(C.1)

(b) Cantilever beam:

$$\begin{aligned}{}[G(P)]= \begin{bmatrix} 1 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1&{} 1 &{} 1\\ 0 &{} 1 &{} {m_{1}} &{} {m_{2}} &{} {m_{3}} &{} {n_{1}}&{} {n_{2}} &{} {n_{3}}\\ 0 &{} 0 &{} {m_{1}}^2 &{} {m_{2}}^2 &{} {m_{3}}^2 &{} {n_{1}}^2&{} {n_{2}}^2 &{} {n_{3}}^2\\ 0 &{} 0 &{} {m_{1}}^3 &{} {m_{2}}^3 &{} {m_{3}}^3 &{} {n_{1}}^3&{} {n_{2}}^3 &{} {n_{3}}^3\\ 0 &{} 0 &{} p_{3}{e}^{(m_{1}L)}&{}p_{4}{e}^{(m_{2}L)}&{}p_{5}{e}^{(m_{3}L)}&{}p_{6}{e}^{(n_{1}L)}&{}p_{7}{e}^{(n_{2}L)}&{}p_{8}{e}^{(n_{3}L)}\\ 0 &{} 0 &{} r_{3}{e}^{(m_{1}L)}&{}r_{4}{e}^{(m_{2}L)}&{}r_{5}{e}^{(m_{3}L)}&{}r_{6}{e}^{(n_{1}L)}&{}r_{7}{e}^{(n_{2}L)}&{}r_{8}{e}^{(n_{3}L)}\\ 0 &{} 0 &{} q_{3}{e}^{(m_{1}L)}&{}q_{4}{e}^{(m_{2}L)}&{}q_{5}{e}^{(m_{3}L)}&{}q_{6}{e}^{(n_{1}L)}&{}q_{7}{e}^{(n_{2}L)}&{}q_{8}{e}^{(n_{3}L)}\\ 0 &{} 0 &{} m_{1}^{4}{e}^{(m_{1}L)} &{} m_{2}^{4}{e}^{(_{2}L)} &{} m_{3}^{4}{e}^{(m_{3}L)} &{} n_{1}^{4}{e}^{(n_{1}L)} &{} n_{2}^{4}{e}^{(n_{2}L)} &{} n_{3}^{4}{e}^{(n_{3}L)}\\ \end{bmatrix} \end{aligned}$$
(C.2)

(c) Clamped beam:

$$\begin{aligned}{}[G(P)]= \begin{bmatrix} 1 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1&{} 1 &{} 1\\ 1 &{} L &{} {e}^{(m_{1}L)} &{} {e}^{(m_{2}L)} &{} {e}^{(m_{3}L)} &{} {e}^{(n_{1}L)}&{} {e}^{(n_{2}L)} &{} {e}^{(n_{3}L)} \\ 0 &{} 1 &{} {m_{1}} &{} {m_{2}} &{} {m_{3}} &{} {n_{1}}&{} {n_{2}} &{} {n_{3}}\\ 0 &{} 1 &{} {m_{1}}{e}^{(m_{1}L)} &{} {m_{2}}{e}^{(m_{2}L)} &{} {m_{3}}{e}^{(m_{3}L)} &{} {n_{1}}{e}^{(n_{1}L)}&{} {n_{2}}{e}^{(n_{2}L)} &{} {n_{3}}{e}^{(n_{3}L)} \\ 0 &{} 0 &{} {m_{1}}^2 &{} {m_{2}}^2 &{} {m_{3}}^2 &{} {n_{1}}^2&{} {n_{2}}^2 &{} {n_{3}}^2\\ 0 &{} 0 &{} m_{1}^{2}{e}^{(m_{1}L)} &{} m_{2}^{2}{e}^{(m_{2}L)} &{} m_{3}^{2}{e}^{(m_{3}L)} &{} n_{1}^{2}{e}^{(n_{1}L)} &{} n_{2}^{2}{e}^{(n_{2}L)} &{} n_{3}^{2}{e}^{(n_{3}L)}\\ 0 &{} 0 &{} {m_{1}}^3 &{} {m_{2}}^3 &{} {m_{3}}^3 &{} {n_{1}}^3&{} {n_{2}}^3 &{} {n_{3}}^3\\ 0 &{} 0 &{} m_{1}^{3}{e}^{(m_{1}L)} &{} m_{2}^{3}{e}^{(m_{2}L)} &{} m_{3}^{3}{e}^{(m_{3}L)} &{} n_{1}^{3}{e}^{(n_{1}L)} &{} n_{2}^{3}{e}^{(n_{2}L)} &{} n_{3}^{3}{e}^{(n_{3}L)}\\ \end{bmatrix} \end{aligned}$$
(C.3)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ishaquddin, M., Gopalakrishnan, S. Static, stability and dynamic analyses of second strain gradient elastic Euler–Bernoulli beams. Acta Mech 232, 1425–1444 (2021). https://doi.org/10.1007/s00707-020-02902-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-020-02902-5

Search

Navigation