In-plane responses of multilayer FG-GPLRC curved beams in thermal environment under moving load

Abstract

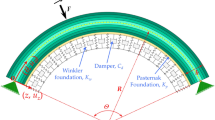
As a first attempt, the transient in-plane responses of multilayer functionally graded graphene platelet-reinforced composite (FG-GPLRC) curved beams in thermal environment under a concentrated moving load are investigated. The motion equations are derived based on the first-order shear deformation theory by considering the influences of the initial thermal stresses. The Chebyshev–Ritz method together with Newmark’s time integration scheme is employed to solve the equations of motion with different sets of boundary conditions. In this regard, the Chebyshev polynomials in conjunction with suitable boundary functions are used to construct the admissible functions of the field variables. Each layer is built up from an isotropic homogeneous polymer matrix reinforced by uniformly distributed and randomly oriented graphene platelets (GPLs). The multilayer FG-GPLRC curved beams are composed of a sufficient number of GPL-reinforced layers to create gradation without abrupt change in their material properties along the beam thickness direction. After validating the approach, the effects of moving load velocity, the GPL weight fraction and through-the-thickness distributions, total number of GPLRC curved beam layers, the curved beam geometric parameters, thermal environment and edge boundary conditions on the dynamic behavior of FG-GPLRC curved beams subjected to a moving load are studied.

Appendices

Appendix A. The strain–displacement relations

Based on the three-dimensional elasticity theory, the strain–displacement relations in the polar coordinate system can be summarized as

$$\begin{aligned} \varepsilon _{\theta \theta }&= \varepsilon _{\theta \theta }^{L}+\varepsilon _{\theta \theta }^\mathrm{NL},\quad \varepsilon _{\theta \theta }^{L}=\frac{1}{r}\left( u+\frac{\partial v}{\partial \theta } \right) ,\quad \varepsilon _{\theta \theta }^\mathrm{NL}=\frac{1}{2r^{2}}\left[ \left( \frac{\partial v}{\partial \theta }+u \right) ^{2}+ \right. \left. \left( \frac{\partial u}{\partial \theta }-v \right) ^{2} \right] , \\ \gamma _{r\theta }^{L}&= \frac{\partial v}{\partial r}+\frac{1}{r}\left( \frac{\partial u}{\partial \theta }-v \right) . \end{aligned}$$

(A.a--d)

Appendix B. The elements of mass matrix, stiffness matrix and force vector

The elements of the mass and stiffness sub-matrices, and force vectors are as follows, respectively,

$$\begin{aligned} \left( {{\varvec{M}}}_{{\varvec{AA}}} \right) _{ij} = I_{0}D_{i,j},\quad \left( {{\varvec{M}}}_{{\varvec{BB}}} \right) _{ij}= I_{0}D_{i,j},\quad \left( {{\varvec{M}}}_{{{\varvec{B}}}C} \right) _{ij}= I_{1}D_{i,j},\quad \left( {{\varvec{M}}}_{{\varvec{CC}}} \right) _{ij}= I_{2}D_{i,j},\quad \left( {{\varvec{M}}}_{{{\varvec{B}}}C} \right) _{ji}= \left( {{\varvec{M}}}_{C{{\varvec{B}}}} \right) _{ij}, \end{aligned}$$

(B.1a--e)

$$\begin{aligned} \left( {{\varvec{K}}}_{{\varvec{AA}}} \right) _{ij}&= H_{i,j}^{\vartheta ,0,0}Q_{1}^{-1,0}+\theta _{*}^{2}H_{i,j}^{\vartheta ,1,1}Q_{3}^{-1,0}+S^{0}\left( \theta _{*}^{2}H_{i,j}^{\vartheta ,1,1}+H_{i,j}^{\vartheta ,0,0} \right) , \\ \left( {{\varvec{K}}}_{{\varvec{AB}}} \right) _{ij}&= \theta _{*}\left[ \left( H_{i,j}^{\vartheta ,0,1} \right. Q_{1}^{-1,0} \right. - \left. H_{i,j}^{\vartheta ,1,0}Q_{3}^{-1,0} \right) +\left. S^{0}\left( -H_{i,j}^{\vartheta ,1,0}+H_{i,j}^{\vartheta ,0,1} \right) \right] , \\ \left( {{\varvec{K}}}_{{\varvec{AC}}} \right) _{ij}&= \theta _{*}\left[ \left( H_{i,j}^{\vartheta ,0,1}Q_{1}^{-1,1} \right. +H_{i,j}^{\vartheta ,1,0}\left. \left[ {-Q}_{3}^{-1,1}+Q_{3}^{0,0} \right] \right) +S^{1} \right. \left. \left( -H_{i,j}^{\vartheta ,1,0}+H_{i,j}^{\vartheta ,0,1} \right) \right] , \end{aligned}$$

(B.2a--i)

$$\begin{aligned} \left( {{\varvec{K}}}_{{\varvec{BB}}} \right) _{ij}&= \theta _{*}^{2}H_{i,j}^{\vartheta ,1,1}Q_{1}^{-1,0}+H_{i,j}^{\vartheta ,0,0}Q_{3}^{-1,0}+S^{0}\left( H_{i,j}^{\vartheta ,0,0}+\theta _{*}^{2}H_{i,j}^{\vartheta ,1,1} \right) , \\ \left( {{\varvec{K}}}_{{\varvec{BC}}} \right) _{ij}&= \theta _{*}^{2}H_{i,j}^{\vartheta ,1,1}Q_{1}^{-1,1}+H_{i,j}^{\vartheta ,0,0}\left( Q_{3}^{-1,1}-Q_{3}^{0,0} \right) +S^{1}\left( H_{i,j}^{\vartheta ,0,0} \right. +\left. \theta _{*}^{2}H_{i,j}^{\vartheta ,1,1} \right) , \\ \left( {{\varvec{K}}}_{{\varvec{CC}}} \right) _{i,j}&= \theta _{*}^{2}H_{i,j}^{\vartheta ,1,1}Q_{1}^{-1,2}+H_{i,j}^{\vartheta ,0,0}\left( Q_{3}^{1,0}+Q_{3}^{-1,2}-2Q_{3}^{0,1} \right) +S^{2}\left( H_{i,j}^{\vartheta ,0,0}+ \right. \left. \theta _{*}^{2}H_{i,j}^{\vartheta ,1,1} \right) , \\ \left( {{\varvec{K}}}_{{\varvec{AB}}} \right) _{ij}&= \left( {{\varvec{K}}}_{{\varvec{BA}}} \right) _{ji}\left( {{\varvec{K}}}_{{\varvec{AC}}} \right) _{ij}=\left( {{\varvec{K}}}_{{\varvec{CA}}} \right) _{ji}, \left( {{\varvec{K}}}_{{\varvec{BC}}} \right) _{ij}=\left( {{\varvec{K}}}_{{\varvec{CB}}} \right) _{ji}. \\ \left( {\mathbf{F }}_{{\mathbf{A }}} \right) _{i}&= F(t)J_{i}^{\vartheta }\left( {\mathbf{F }}_{{\mathbf{B }}} \right) _{i}=\left( {\mathbf{F }}_{{\mathbf{C }}} \right) _{i}=0, \end{aligned}$$

(B.3a--c)

where

$$\begin{aligned} D_{i,j}^{\vartheta }&= \int _{-1}^{+1} \left[ F_\mathrm{B}^{\vartheta }(\beta )P_{i}(\beta ) \right] \left[ F_\mathrm{B}^{\vartheta }(\beta )P_{j}(\beta ) \right] \text {d}\beta ,\quad I^{\eta } =b\sum \limits _{i=1}^{N_\mathrm{L}} {\int _{r_{i}}}^{r_{i+1}} {\rho _{i}(r)} r\chi ^{\eta }dr, \\ H_{i,j}^{\vartheta ,a,{{\bar{a}}} }&= \int _{-1}^{+1} \frac{d^{a}\left[ F_\mathrm{B}^{\vartheta }\left( \beta \right) P_{i}\left( \beta \right) \right] }{\text {d}\beta ^{a}} \frac{d^{{{\bar{a}}}}\left[ F_\mathrm{B}^{\vartheta }\left( \beta \right) P_{j}\left( \beta \right) \right] }{\text {d}\beta ^{{{\bar{a}}}}}\text {d}\beta , \\ \left( Q_{1}^{\vartheta ,\eta }, \right. \left. Q_{3}^{\vartheta ,\eta } \right)&= b\sum \limits _{i=1}^{N_\mathrm{L}} {\int _{r_{i}}}^{r_{i+1}} {\left( \frac{E_{i}(r)}{1-\nu _{ci}^{2}(r)} \right. ,} \left. \frac{E_{i}(r)}{2\left( 1+\nu _{ci}(r) \right) } \right) r^{\vartheta }\chi ^{\eta }dr,\\ S^{\eta }&=\frac{b}{2}\sum \limits _{i=1}^{N_\mathrm{L}} \int _{r_{i}}^{r_{i+1}} {\alpha _{i}^{*}(r)\varDelta T} \frac{1}{r}\chi ^{\eta }dr, \\ \alpha _{i}^{*}(r)&= -\,\left( 3\mu _{i}(r)+2G_{i}(r) \right) \alpha _{i}(r), \quad J_{i}^{\vartheta }=\int _{-1}^{+1} \left[ F_\mathrm{B}^{\vartheta }(\beta )P_{i}(\beta ) \right] \text {d}\beta , \left( \vartheta =U,V,\varPhi \right) , \\ \theta _{*}&= \frac{2}{\theta _{0}}, \end{aligned}$$

(B.4a--h)

where if $i=1,r_{1}=R_{i}$ and if $i=N_\mathrm{L}+1$, $r_{N_\mathrm{L}+1}=R_\mathrm{o}$.