Nonlinear buckling and postbuckling of sandwich FGM cylindrical shells reinforced by spiral stiffeners under torsion loads in thermal environment

Abstract

The main purpose of this paper is the investigation of the nonlinear torsional buckling and postbuckling of sandwich functionally graded cylindrical shells with the von Karman large deflection nonlinearities under thermal effect by an analytical method. The shell skin is reinforced by stringer, circular ring and spiral stiffeners, the material properties of shell skin and stiffeners are assumed to vary continuously through the thickness. The very large effect of spiral stiffeners on the buckling load-carrying capacity of a cylindrical shell in comparison with orthogonal stiffeners is clearly proved in numerical investigations. Based on the Donnell shell theory and the improved smeared stiffener technique for both thermal and mechanical terms of spiral stiffeners, the equilibrium equations of the shell are established in this paper. By using the Galerkin method, the postbuckling curves and critical buckling loads are obtained. The effects of temperature change, stiffeners, material and dimensional parameters on the nonlinear torsional buckling and postbuckling of shell are numerically analyzed.

Appendices

Appendix I

In Eqs. (9) and (10),

$$\begin{aligned} e_{11}= & {} \frac{E_1 }{1-v^{2}}+\frac{E_{1s} b_s }{d_s }+2\frac{E_{1l} b_l }{d_l }\cos ^{4}\alpha ,\,\, e_{12} =\frac{vE_1 }{1-v^{2}}+2\frac{E_{1l} b_l }{d_l }\sin ^{2}\alpha \cos ^{2}\alpha ,\nonumber \\ e_{14}= & {} \frac{E_2 }{1-v^{2}}+\frac{E_{2s} b_s }{d_s }+2\frac{E_{2l} b_l }{d_l }\cos ^{4}\alpha ,\,\, e_{15} =\frac{vE_2 }{1-v^{2}}+\frac{E_{2s} b_s }{d_s }+2\frac{E_{2l} b_l }{d_l }\sin ^{2}\alpha \cos ^{2}\alpha ,\nonumber \\ e_{22}= & {} \frac{E_1 }{1-v^{2}}+\frac{E_{1r} b_r }{d_r }+2\frac{E_{1l} b_l }{d_l }\sin ^{4}\alpha ,\,\, e_{24} =\frac{vE_2 }{1-v^{2}}+2\frac{E_{2l} b_l }{d_l }\sin ^{2}\alpha \cos ^{2}\alpha ,\nonumber \\ e_{25}= & {} \frac{E_2 }{1-v^{2}}+\frac{E_{2r} b_r }{d_r }+2\frac{E_{2l} b_l }{d_l }\sin ^{4}\alpha ,\,\, e_{33} =\frac{E_1 }{2(1+v)}+2\frac{E_{1l} b_l }{d_l }\sin ^{2}\alpha \cos ^{2}\alpha ,\nonumber \\ e_{36}= & {} \frac{E_2 }{1+v}+4\frac{E_{2l} b_l }{d_l }\sin ^{2}\alpha \cos ^{2}\alpha ,\,\, e_{44} =\frac{E_3 }{1-v^{2}}+\frac{E_{3s} b_s }{d_s }+2\frac{E_{3l} b_l }{d_l }\cos ^{4}\alpha ,\nonumber \\ e_{45}= & {} \frac{vE_3 }{1-v^{2}}+2\frac{E_{3l} b_l }{d_l }\sin ^{2}\alpha \cos ^{2}\alpha ,\,\, e_{55} =\frac{E_3 }{1-v^{2}}+\frac{E_{3r} b_r }{d_r }+2\frac{E_{3l} b_l }{d_l }\sin ^{4}\alpha ,\nonumber \\ e_{66}= & {} \frac{E_3 }{1+v}+4\frac{E_{3l} b_l }{d_l }\sin ^{2}\alpha \cos ^{2}\alpha ,\,\, e_{63} =\frac{E_2 }{2(1+v)}+2\frac{E_{2l} b_l }{d_l }\sin ^{2}\alpha \cos ^{2}\alpha , \end{aligned}$$

(I.1)

in which

Case A:

$$\begin{aligned} E_1= & {} E_c h+E_{mc} \left( {h_c +\frac{h_t }{k_t +1} +\frac{h_b }{k_b +1}} \right) ,\nonumber \\ E_2= & {} E_{mc} \left[ \frac{h_c (h_t -h_b)}{2} +\frac{h_t^2 }{k_t +2}-\frac{hh_t }{2(k_t +1)} -\frac{h_b^2 }{k_b +2}+\frac{hh_b }{2(k_b +1)}\right] ,\nonumber \\ E_3= & {} E_c \frac{h^{3}}{12}+E_{mc} \left[ \frac{(h-2h_b)^{3} +(h-2h_t)^{3}}{24}+\frac{h_t^3 }{k_t +3}-\frac{hh_t^2 }{k_t +2} +\frac{h^{2}h_t }{4(k_t +1)}+\right. \nonumber \\&+\left. \frac{h_b^3 }{k_b +3}-\frac{hh_b^2 }{k_b +2} +\frac{h^{2}h_b}{4(k_b +1)}\right] , \nonumber \\ \phi _1= & {} \frac{1}{1-v}\int \limits _{-h/2}^{h/2} E_{sh} \alpha _{sh} \Delta T \mathrm{d}z =\frac{1}{1-v}\phi _1^{sh} . \end{aligned}$$

(I.2)

If $\Delta T=\mathrm{const.}$, then

$$\begin{aligned} \phi _1^{sh}= & {} \Delta T\left[ \begin{array}{l} E_c \alpha _c h+(E_m \alpha _m -E_c \alpha _c)h_c \\ +(E_c \alpha _{mc} +E_{mc} \alpha _c)\left( \frac{h_t }{k_t +1} +\frac{h_b }{k_b +1}\right) +E_{mc} \alpha _{mc} \left( \frac{h_t }{2k_t +1}+\frac{h_b }{2k_b +1}\right) \\ \end{array}\right] , \end{aligned}$$

(I.3)

$$\begin{aligned} E_{1s}= & {} E_c h_s +\frac{E_{mc}h_s }{k_s +1},\nonumber \\ E_{2s}= & {} \frac{E_c}{2}hh_s \left( \frac{h_s }{h}+1\right) +E_{mc}h_s h\left( \frac{1}{k_s +2}\frac{h_s }{h} +\frac{1}{2k_s +2}\right) ,\nonumber \\ E_{3s}= & {} \frac{E_c}{3}h_s^3 \left( \frac{3}{4}\frac{h^{2}}{h_s^2} +\frac{3}{2}\frac{h}{h_s }+1\right) +E_{mc}h_s^3 \left( \frac{1}{k_s +3}+\frac{1}{k_s +2}\frac{h}{h_s} +\frac{1}{4(k_s +1)}\frac{h^{2}}{h_s^2}\right) ,\nonumber \\ \phi _{1x}^T= & {} \frac{b_s }{d_s }\int \limits _{h/2}^{h/2+h_s } {E_s \alpha _s \Delta T} \mathrm{d}z+\frac{b_l }{d_l }\int \limits _{h/2}^{h/2+h_l } {2E_l \alpha _l (\hbox {cos}^{6}\alpha +\hbox {sin}^{2}\alpha \hbox {cos}^{2}\alpha )\Delta T} \mathrm{d}z,\nonumber \\ E_{1r}= & {} E_ch_r +\frac{E_{mc}h_r }{k_r +1},\nonumber \\ E_{2r}= & {} \frac{E_c}{2}hh_r \left( \frac{h_r }{h}+1\right) +E_{mc}h_r h\left( \frac{1}{k_r +2}\frac{h_r }{h} +\frac{1}{2k_r +2}\right) ,\nonumber \\ E_{3r}= & {} \frac{E_c}{3}h_r^3 \left( \frac{3}{4}\frac{h^{2}}{h_r^2} +\frac{3}{2}\frac{h}{h_r }+1\right) +E_{mc}h_r^3 \left( \frac{1}{k_r +3}+\frac{1}{k_r +2}\frac{h}{h_r } +\frac{1}{4(k_r +1)}\frac{h^{2}}{h_r^2}\right) ,\nonumber \\ \phi _{1y}^T= & {} \frac{b_r }{d_r }\int \limits _{h/2}^{h/2+h_r } E_r \alpha _r \Delta T \mathrm{d}z+\frac{b_l }{d_l }\int \limits _{h/2}^{h/2+h_l} 2E_l \alpha _l \left( {\hbox {sin}^{6}\alpha +\hbox {sin}^{2}\alpha \hbox {cos}^{2}\alpha } \right) \Delta T \mathrm{d}z,\nonumber \\ E_{1l}= & {} E_c h_l +E_{mc} h_l \frac{1}{k_l +1},\nonumber \\ E_{2l}= & {} \frac{E_c }{2}h_l (h+h_l)+E_{mc} h_l^2 \left( \frac{1}{k_l +2}+\frac{h}{2h_l}\frac{1}{k_l +1}\right) ,\nonumber \\ E_{3l}= & {} \frac{E_c }{3}\left[ \left( \frac{h}{2}+h_l\right) ^{3} -\frac{h^{3}}{8}\right] +E_{mc} h_l^3 \left( \frac{1}{k_l +3} +\frac{h}{h_l }\frac{1}{k_l +2}+\frac{h^{2}}{4h_l^2} \frac{1}{k_l +1}\right) , \end{aligned}$$

(I.4)

If $\Delta T = \mathrm{const.}$, then

$$\begin{aligned} \phi _{1x}^T= & {} \frac{b_s}{d_s}\Delta Th_s \left[ E_c \alpha _c +\frac{1}{k_s +1}(E_c \alpha _{mc} +E_{mc} \alpha _c) +\frac{1}{2k_s +1}E_{mc} \alpha _{mc}\right] \nonumber \\&+2\frac{b_l }{d_l }\Delta Th_l \left[ \begin{array}{l} E_c \alpha _c +\frac{1}{k_l +1}(E_c \alpha _{mc} +E_{mc} \alpha _c ) \\ +\frac{1}{2k_l +1}E_{mc} \alpha _{mc} \\ \end{array}\right] (\hbox {cos}^{6}\alpha +\hbox {sin}^{2}\alpha \hbox {cos}^{2}\alpha ), \nonumber \\ \phi _{1y}^T= & {} \frac{b_r }{d_r }\Delta Th_r \left[ E_c \alpha _c +\frac{1}{k_r +1}(E_c \alpha _{mc} +E_{mc} \alpha _c) +\frac{1}{2k_r +1}E_{mc} \alpha _{mc}\right] \nonumber \\&+2\frac{b_l }{d_l }\Delta Th_l \left[ \begin{array}{l} E_c \alpha _c +\frac{1}{k_l +1}(E_c \alpha _{mc} +E_{mc} \alpha _c) \\ +\frac{1}{2k_l +1}E_{mc} \alpha _{mc} \\ \end{array}\right] (\hbox {sin}^{6}\alpha +\hbox {sin}^{2}\alpha \hbox {cos}^{2}\alpha ). \end{aligned}$$

(I.5)

Case B: The expressions are similar to case A by replacing $E_c$ with $E_m$ and $\alpha _c$ with $\alpha _m$.

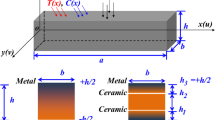
In the above, $d_s ,d_r$ and $d_l$ are the distances between two stringers, rings and spiral, respectively. Also, $b_s$, $b_r$ and $b_l$ denote widths of stiffeners, respectively. The $h_s$, $h_r$ and $b_l$ represent the height of the stiffeners (Fig. 1).

Appendix II

In Eqs. (11) and (12),

$$\begin{aligned} \Delta= & {} e_{22} e_{11} -e_{12}^2 ,\,\, e_{22}^{*} =e_{22} /\Delta ,\,\, e_{12}^{*} =e_{12} /\Delta ,\,\, e_{14}^{*} =(e_{12}e_{24} -e_{22} e_{14})/\Delta ,\nonumber \\ e_{15}^{*}= & {} (e_{12} e_{25} -e_{22} e_{15})/\Delta ,\,\, e_{16}^{*} =(e_{22} -e_{12})/\Delta ,\,\, e_{11}^{*} =e_{11} /\Delta ,\nonumber \\ e_{24}^{*}= & {} (e_{12} e_{14} -e_{11} e_{24})/\Delta ,\,\, e_{25}^{*} =(e_{12} e_{15} -e_{11} e_{25})/\Delta ,\,\, e_{26}^{*} =(e_{11} -e_{12})/\Delta ,\nonumber \\ e_{33}^{*}= & {} 1/e_{33} ,\,\, e_{36}^{*} =e_{36} /e_{33} . \end{aligned}$$

(II.1)

$$\begin{aligned} H_{14}^{*}= & {} e_{14} e_{22}^{*} -e_{24} e_{12}^{*} ,\,\, H_{44}^{*} =e_{44} +e_{24} e_{24}^{*} +e_{14} e_{14}^{*} ,\,\, H_{24}^{*} =e_{24} e_{11}^{*} -e_{14} e_{12}^{*} ,\nonumber \\ H_{45}^{*}= & {} e_{14} e_{15}^{*} +e_{24} e_{25}^{*} +e_{45} ,\,\, H_{46}^{*} =e_{14} e_{16}^{*} +e_{24} e_{26}^{*} ,\,\, H_{15}^{*} =e_{15} e_{22}^{*} -e_{25} e_{12}^{*} ,\nonumber \\ H_{54}^{*}= & {} e_{15} e_{14}^{*} +e_{25} e_{24}^{*} +e_{45} ,\,\, H_{25}^{*} =e_{25} e_{11}^{*} -e_{15} e_{12}^{*} ,\,\, H_{55}^{*} =e_{15} e_{15}^{*} +e_{25} e_{25}^{*} +e_{55} ,\nonumber \\ H_{56}^{*}= & {} e_{15} e_{16}^{*} +e_{25} e_{26}^{*} ,\,\, H_{63}^{*} =e_{63} e_{33}^{*} ,\,\, H_{66}^{*} =e_{66} -e_{63} e_{36}^{*} , \end{aligned}$$

(II.2)

Appendix III

In Eqs. (20, 24, 25),

$$\begin{aligned} T_1= & {} \frac{T_{01} L^{4}}{16S_{11} (m\pi )^{4}} =Q_{11} W_2 +Q_{12} W_1^2 ,\nonumber \\ T_2= & {} \frac{T_{02} R^{4}}{16n^{4}[S_{11} \lambda ^{4} +S_{12} \lambda ^{2}+S_{13}]}=Q_{21} W_1^2 ,\nonumber \\ T_3= & {} \frac{T_{03} R^{4}}{n^{4}\left[ S_{11} \left( \frac{m\pi R}{nL} -\lambda \right) ^{4}+S_{12} \left( \frac{m\pi R}{nL}-\lambda \right) ^{2} +S_{13}\right] }=Q_{31} W_1 +Q_{32} W_1 W_2 ,\nonumber \\ T_4= & {} \frac{T_{04} R^{4}}{n^{4}\left[ S_{11} \left( \frac{m\pi R}{nL} +\lambda \right) ^{4}+S_{12} \left( \frac{m\pi R}{nL}+\lambda \right) ^{2} +S_{13}\right] }=Q_{41} W_1 +Q_{42} W_1 W_2 ,\nonumber \\ T_5= & {} \frac{T_{05} R^{4}}{n^{4}\left[ S_{11} \left( 3\frac{m\pi R}{nL} +\lambda \right) ^{4}+S_{12} \left( 3\frac{m\pi R}{nL}+\lambda \right) ^{2} +S_{13}\right] }=Q_5 W_1 W_2 ,\nonumber \\ T_6= & {} \frac{-T_{05} R^{4}}{n^{4}\left[ S_{11} \left( 3\frac{m\pi R}{nL} -\lambda \right) ^{4}+S_{12} \left( 3\frac{m\pi R}{nL}-\lambda \right) ^{2} +S_{13}\right] }=Q_6 W_1 W_2 , \end{aligned}$$

(III.1)

in which

$$\begin{aligned} Q= & {} \left( \frac{m\pi }{L}\right) ^{2}+\frac{n^{2}\lambda ^{2}}{R^{2}},\,\, Q_{11} =\frac{4S_{11} (m\pi )^{2}R-L^{2}}{8S_{11} (m\pi )^{2}R},\,\, Q_{12} =\frac{(nL)^{2}}{32S_{11} (m\pi )^{2}R^{2}},\nonumber \\ Q_{21}= & {} \frac{(m\pi R)^{2}}{32(nL)^{2}[S_{11} \lambda ^{4} +S_{12} \lambda ^{2}+S_{13}]},\nonumber \\ Q_{31}= & {} \frac{\frac{S_{14}}{2}\left[ P^{2}+\left( 2\frac{mn\pi }{LR} \lambda \right) ^{2}\right] -\frac{P}{2}\left( \frac{1}{R}-S_{15} \frac{n^{2}}{R^{2}}\right) +\frac{S_{16} }{2}\frac{n^{4}}{R^{4}} +\frac{mn\pi }{LR}\lambda \left[ -2S_{14} P+\frac{1}{R}-S_{15} \frac{n^{2}}{R^{2}}\right] }{\frac{n^{4}}{R^{4}}\left[ S_{11} \left( \frac{m\pi R}{nL}-\lambda \right) ^{4}+S_{12} \left( \frac{m\pi R}{nL}-\lambda \right) ^{2}+S_{13}\right] },\nonumber \\ Q_{32}= & {} \frac{(m\pi R)^{2}}{2(nL)^{2}\left[ S_{11} \left( \frac{m\pi R}{nL}-\lambda \right) ^{4}+S_{12} \left( \frac{m\pi R}{nL}-\lambda \right) ^{2}+S_{13}\right] },\nonumber \\ Q_{41}= & {} \frac{-S_{14} \left[ P^{2} +\left( 2\frac{mn\pi }{LR}\lambda \right) ^{2}\right] +\frac{P}{R}\left( 1-S_{15} \frac{n^{2}}{R}\right) -S_{16} \frac{n^{4}}{R^{4}}+2\frac{mn\pi }{LR}\lambda \left[ -2S_{14} P+\frac{1}{R}-S_{15} \frac{n^{2}}{R^{2}}\right] }{2\frac{n^{4}}{R^{4}}\left[ S_{11} \left( \frac{m\pi R}{nL}+\lambda \right) ^{4} +S_{12} \left( \frac{m\pi R}{nL}+\lambda \right) ^{2}+S_{13}\right] },\nonumber \\ Q_{42}= & {} \frac{-(m\pi R)^{2}}{2(nL)^{2}\left[ S_{11} \left( \frac{m\pi R}{nL} +\lambda \right) ^{4}+S_{12} \left( \frac{m\pi R}{nL}+\lambda \right) ^{2} +S_{13} \right] },\nonumber \\ Q_5= & {} \frac{(m\pi R)^{2}}{2(nL)^{2}\left[ S_{11}\left( 3\frac{m\pi R}{nL} +\lambda \right) ^{4}+S_{12} \left( 3\frac{m\pi R}{nL}+\lambda \right) ^{2} +S_{13} \right] },\nonumber \\ Q_6= & {} \frac{-(m\pi R)^{2}}{2(nL)^{2}\left[ S_{11}\left( 3\frac{m\pi R}{nL} -\lambda \right) ^{4}+S_{12} \left( 3\frac{m\pi R}{nL}-\lambda \right) ^{2} +S_{13} \right] }, \end{aligned}$$

(III.2)

$$\begin{aligned} H_1= & {} F_{11} \left[ \left( \frac{(m\pi )^{2}}{L^{2}} +\frac{n^{2}}{R^{2}}\lambda ^{2}\right) ^{2} +\left( 2\frac{mn\pi }{LR}\lambda \right) ^{2}\right] +F_{12} \frac{n^{2}}{R^{2}}\left( \frac{(m\pi )^{2}}{L^{2}} +\frac{n^{2}}{R^{2}}\lambda ^{2}\right) +F_{13} \frac{n^{4}}{R^{4}} \nonumber \\&-Q_{31} \frac{n^{4}}{R^{4}}\left[ F_{14} \left( \frac{m\pi R}{nL}-\lambda \right) ^{4} +\left( F_{15} -\frac{R}{n^{2}}\right) \left( \frac{m\pi R}{nL}-\lambda \right) ^{2}+F_{16}\right] \nonumber \\&+Q_{41} \frac{n^{4}}{R^{4}}\left[ F_{14} \left( \frac{m\pi R}{nL}+\lambda \right) ^{4} +\left( F_{15} -\frac{R}{n^{2}}\right) \left( \frac{m\pi R}{nL}+\lambda \right) ^{2}+F_{16}\right] , \nonumber \\ H_2= & {} -Q_{32} \frac{n^{4}}{R^{4}}\left[ F_{14} \left( \frac{m\pi R}{nL}-\lambda \right) ^{4} +\left( F_{15} -\frac{R}{n^{2}}\right) \left( \frac{m\pi R}{nL}-\lambda \right) ^{2}+F_{16}\right] \nonumber \\&+\left( \frac{mn\pi }{LR}\right) ^{2} (-Q_{31} +Q_{41} -2Q_{11})+P_{42} \frac{n^{4}}{R^{4}} \left[ F_{14} \left( \frac{m\pi R}{nL}+\lambda \right) ^{4}\right. \nonumber \\&\left. +\left( F_{15} -\frac{R}{n^{2}}\right) \left( \frac{m\pi R}{nL}+\lambda \right) ^{2}+F_{16}\right] , \nonumber \\ H_3= & {} -2(Q_{21} +Q_{12})\left( \frac{mn\pi }{LR}\right) ^{2},\,\, H_4 =(-Q_{32} +Q_{42} -Q_5 +Q_6)\left( \frac{mn\pi }{LR}\right) ^{2},\nonumber \\ H_5= & {} -8 \frac{(m\pi )^{2}}{L^{2}}\left[ -2F_{11} \frac{(m\pi )^{2}}{L^{2}}+\left( 4F_{14} \frac{(m\pi )^{2}}{L^{2}} -\frac{1}{R}\right) Q_{11}\right] ,\nonumber \\ H_6= & {} 8\frac{(m\pi )^{2}}{L^{2}}Q_{12} \left( 4F_{14} \frac{(m\pi )^{2}}{L^{2}}-\frac{1}{R}\right) +2(Q_{31} -Q_{41})\frac{(mn\pi )^{2}}{(LR)^{2}},\nonumber \\ H_7= & {} 2\frac{(mn\pi )^{2}}{(LR)^{2}}(-Q_{32} +Q_{42} -Q_5 +Q_6). \end{aligned}$$

(III.3)