Generalized reciprocity theorems for infinitesimal deformations superimposed upon finite deformations of rods: the plane problem

Abstract

The present paper is concerned with bending of extensible and shear-deformable rods, where we treat the case of plane deformations. Our emphasis is laid upon infinitesimal deformations superimposed upon finite deformations. In this framework, we focus on deriving generalized reciprocity theorems that must hold with respect to the superimposed infinitesimal deformations, when produced by different types of loadings. Besides imposed distributed and concentrated force and moment loadings, we consider the action of eigenstrains. Moreover, we also take into account the presence of jumps in kinematic entities, particularly concerning jumps of axial rod positions and of cross-sectional rotations. We first derive local and global universal reciprocity relations, which must hold for rods made of any material. The global universal relation then is specialized to the case of hyperelastic rods. From the latter relation, we prove that reciprocity theorems known from the linear theory, such as the theorems of Betti, Maxwell and Land, as well as Maysel’s formula, formally do hold for infinitesimal deformations superimposed upon finite deformations. As a formulation that appears to be novel also with respect to the purely linear theory, we present a combination of Maysel’s formula with the theory of Land, the former dealing with eigenstrains, the latter involving jumps in kinematic entities.

1 Introduction

The present paper is concerned with bending of extensible and shear-deformable rods. For a comprehensive presentation of the theory of rods, see the book on the mechanics of deformable solids [1] by V.V. Eliseev, to whom our contribution is devoted in grateful memory.

Subsequently, we treat the case of plane deformations of rods, the finite strain theory of which dates back to Reissner [2]. Our emphasis is laid upon infinitesimal deformations superimposed upon finite deformations. For fundamentals of this type of superposition, see Knops and Wilkes [3]. In the present contribution, we focus on deriving generalized reciprocity theorems that must hold with respect to the superimposed infinitesimal deformations, when produced by different loadings. Besides imposed distributed and concentrated force and moment loadings, we also consider the action of eigenstrains. Moreover, we also take into account the presence of jumps in kinematic quantities, particularly concerning jumps of axial rod positions and of cross-sectional rotations.

Our contribution is organized as follows. In Sect. 2, we present the local relations of equilibrium for the finite strain case, as well as the local incremental equilibrium relations that hold for superposed infinitesimal deformations. Following and extending the procedure for rods rigid in shear presented by DaDeppo [4], the incremental equilibrium relations are derived as time rate forms of the equilibrium relations for the finite strain case. In Sect. 3, we derive a local virtual work relation by multiplying the local incremental equilibrium relations with proper infinitesimal virtual deformation rates. This relation is further simplified by introducing the rates of generalized strain measures that were introduced by Reissner [2]. Local and global universal reciprocity relations are eventually derived in Sect. 4. We talk about a universal relation, when it does hold for any constitutive relation of the rod under consideration. In our derivation, we consider the virtual deformation quantities to be produced by a set of virtual internal and external forces and moments, which forms an equilibrium system, likewise to the original incremental problem. We are thus allowed to interchange original and virtual quantities in the local virtual work relation derived before in Sect. 3. This yields an adjoint virtual work relation. Subtracting the two virtual work relations provides the local universal reciprocity relation. The global form of the latter follows by integration along the rod segment under consideration in the reference configuration. In doing so, we also take into account the presence of concentrated external forces and external moments, which correspond to equilibrium relations of jump of the internal forces and moments. Besides of these static jump relations, we also consider kinematic jumps to be present in the infinitesimal superimposed deformations, namely jumps of the position vector or of the cross-sectional rotation at a certain location. Jumps may be present in both, the original and the virtual problem context. The static and kinematic relations of jump enter the universal global reciprocity relation, since integration must be performed piecewise, due to the presence of jumps in the local virtual work relations.

In Sect. 5, we specialize the universal global reciprocity relation derived in Sect. 4 to the case of hyperelastic rods, where we involve the generalized strain measures of Reissner [2], as well as proper integrability relations. We particularly allow the presence of incremental superimposed eigenstrains in the original problem. The generalized reciprocity theorem so obtained includes not only distributed forces and moments as well as jumps in forces and moments, but also eigenstrains and jumps in the kinematic relations. As special forms of this generalized formulation, various reciprocity relations known from the purely linear theory are proved to hold also for infinitesimal deformations superimposed upon finite deformations of shear-deformable and extensible rods, such as the Betti and Maxwell reciprocity theorems, see DaDeppo [4] for rods rigid in shear, and see Ziegler [5] for the linear theory. We further deal with an extension of a reciprocity theorem that involves jumps in the kinematic entities, and which in the purely linear context dates back to Land, see Kurrer [6] for a contemporary exposition. Concerning eigenstrains, we derive an extension of Maysel’s formula of the linear theory of thermoelasticity, see Ziegler and Irschik [7] for the linear theory. As a topic which appears to be novel also with respect to the purely linear theory, we derive a reciprocity formulation that connects superimposed jumps of the virtual kinematic entities with the presence of superimposed eigenstrains in the original problem, and which thus allows to compute eigenstrain-induced internal forces and moments, when the solution due to the superimposed jumps in the kinematic entities is known. In Sect. 6, we finally present numerical and analytic examples for the correctness of the latter formulation.

2 Relations of equilibrium and incremental equilibrium relations

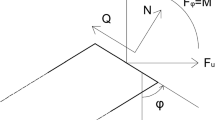
In the course of the present paper, we assume that the deformation of the rod takes place in the (x, z)-plane of a global Cartesian coordinate system with unit base vectors $e_x$, $e_y$, and $e_z$, such that $e_y$ is perpendicular to the plane of deformation. The curved axial coordinate of the rod in the undeformed reference configuration is denoted as $s_0$. The rod may have a curved axis already in the reference configuration. The axial coordinate of the rod in the deformed configuration is called s, see Fig. 1. Studying equilibrium of a rod element of differential axial length ds, but formulating any entities as functions of the reference coordinate $s_0$, one obtains the local relations of equilibrium for the deformed configuration of the rod as, see [1, 2],

$$\begin{aligned}&\displaystyle {\vec {R}}'+\vec {p}=\vec {0}, \end{aligned}$$

(1)

$$\begin{aligned}&\displaystyle {\vec {M}}'+{\vec {r}}'\times \vec {R}+\vec {m}=\vec {0}. \end{aligned}$$

(2)

The derivative of some entity f with respect to $s_0$ is denoted by a prime:

$$\begin{aligned} {f}'=\frac{\partial f}{\partial s_0 }. \end{aligned}$$

(3)

The force vector $\vec {R}$ represents the resultant of the inner forces acting upon a cross section of the rod in the deformed configuration, the position vector of the axis point in this cross section being denoted as $\vec {r}$, see Fig. 1. The moment vector $\vec {M}$ is the resultant couple of the inner forces with respect to the axis point. Note that the deformed configuration may represent a large deformation, possibly accompanied by large displacements from the reference configuration. For the sake of clearness, we will denote this deformed configuration as intermediate configuration in the following. Without going further into details, we assume that the intermediate configuration is infinitesimally superstable, see Knops and Wilkes [3] for details, such that our study on the superposition of infinitesimal deformations upon the intermediate configuration makes practical sense.

Fig. 1

Undeformed and intermediate reference configurations

In the intermediate configuration, we introduce a local cross-sectional coordinate system with unit base vectors $e_1$ and $e_2$, the origin of which is situated at the axis point, and which stems from a positive rotation about the y axis of the global system by the angle $\varphi$, such that

$$\begin{aligned} \vec {e}_1= & {} \vec {e}_x \cos \varphi - \vec {e}_z \sin \varphi , \end{aligned}$$

(4)

$$\begin{aligned} \vec {e}_3= & {} \vec {e}_x \sin \varphi + \vec {e}_z \cos \varphi . \end{aligned}$$

(5)

The corresponding decomposition of the resultants of the inner forces in the local system is written as

$$\begin{aligned}&\displaystyle \vec {R}=R_x \vec {e}_x +R_z \vec {e}_z =N \vec {e}_1 +Q \vec {e}_3, \end{aligned}$$

(6)

$$\begin{aligned}&\displaystyle \vec {M} = M \vec {e}_y. \end{aligned}$$

(7)

Following Reissner [2], the $\vec {e}_1$-direction is taken perpendicular to the cross section in the deformed configuration, such that $\vec {e}_3$ is tangential to the latter, where the angle $\varphi$ is interpreted as the cross-sectional rotation, see Fig. 1. Hence, we call N and Q normal and shear force, respectively, and M is the bending moment. An analogous decomposition for the imposed forces and couples reads:

$$\begin{aligned}&\displaystyle \vec {p}= n \vec {e}_1 +q \vec {e}_3, \end{aligned}$$

(8)

$$\begin{aligned}&\displaystyle \vec {m}= m \vec {e}_y. \end{aligned}$$

(9)

We now formulate the local equilibrium conditions, Eqs. (1) and (2), in the local coordinate system. From Eqs. (4) and (5), the derivatives of the local base vectors with respect to $s_0$ follow as

$$\begin{aligned} \vec {e}_1 ^{\prime }= & {} -{\varphi }' \vec {e}_3, \end{aligned}$$

(10)

$$\begin{aligned} \vec {e}_3 ^{\prime }= & {} {\varphi }' \vec {e}_1. \end{aligned}$$

(11)

The axial deformation gradient vector ${\vec {r}}'$ introduced in Eq. (2) is tangential to the axis,

$$\begin{aligned} {\vec {r}}'=\varLambda \left( { \cos \chi \vec {e}_1 -\sin \chi \vec {e}_3 } \right) . \end{aligned}$$

(12)

The axial stretch is denoted as $\varLambda =\hbox {d}s/\hbox {d}s_0$, and $\chi$ is the shear angle, see Fig. 1. Using Eqs. (6)–(12), the following local form of the relations of equilibrium for the intermediate configuration is obtained from Eqs. (1) and (2):

$$\begin{aligned}&\displaystyle {\vec {R}}'+\vec {p}=\left( {{N}'+{\varphi }' Q+n} \right) \vec {e}_1 +\left( {{Q}'-{\varphi }' N+q} \right) \vec {e}_3 =\vec {0}, \end{aligned}$$

(13)

$$\begin{aligned}&\displaystyle {M}'-\varLambda \left( {Q\cos \chi +N\sin \chi } \right) +m=0. \end{aligned}$$

(14)

We now consider the situation of a quasi-static loading that slowly evolves with time t. Taking into account an infinitesimal deformation with infinitesimal displacements superimposed upon the intermediate configuration, we are seeking for the rate form of Eqs. (13) and (14). Recall that such a superposition makes practical sense, since we have required the intermediate configuration to be infinitesimally superstable [3]. Following considerations by Da Deppo for rods rigid in shear [4], the rate form can be obtained from the equilibrium conditions in Eqs. (13) and (14) by differentiation with respect to the parameter t. Subsequently, the derivative of some entity f with respect to t, holding the place $s_0$ fixed, is denoted by a superimposed dot:

$$\begin{aligned} {\dot{f}}=\frac{\hbox {d}f}{\hbox {d}t}=\left. {\frac{\partial f}{\partial t}} \right| _{s_0 =\hbox {const}}. \end{aligned}$$

(15)

By tacitly skipping $\hbox {d}t$, one then is allowed to interpret this rate ${\dot{f}}$ directly as the increment of f that corresponds to the superimposed infinitesimal deformation under consideration, being expressed as a function of the place $s_0$ in the reference configuration. Analogous to Eqs. (10) and (11), we now have

$$\begin{aligned} \dot{\vec {e}}_1= & {} -\,{\dot{\varphi }} \vec {e}_3, \end{aligned}$$

(16)

$$\begin{aligned} \dot{\vec {e}}_3= & {} {\dot{\varphi }} \vec {e}_1. \end{aligned}$$

(17)

Using the latter relations, the rate forms of Eqs. (13) and (14) can be formulated as

$$\begin{aligned}&\dot{{\vec {R}}'}+\dot{\vec {p}}=\vec {0}, \end{aligned}$$

(18)

$$\begin{aligned}&\dot{{M}'}-{\dot{\varLambda }} \left( {Q\cos \chi +N\sin \chi } \right) \nonumber \\&\quad -\varLambda \left( {{\dot{Q}}\cos \chi +{\dot{N}}\sin \chi } \right) -\varLambda {\dot{\chi }} \left( {-Q\sin \chi +N\cos \chi } \right) +\dot{m}=0. \end{aligned}$$

(19)

For subsequent use, we note the increments of the resultant internal force and its space-wise derivative as

$$\begin{aligned}&\dot{\vec {R}}=\left( {{\dot{N}}+{\dot{\varphi }} Q} \right) \vec {e}_1 +\left( {{\dot{Q}}-{\dot{\varphi }} N} \right) \vec {e}_3, \end{aligned}$$

(20.1)

$$\begin{aligned}&{\dot{\vec {R}}}'=\left( {{{\dot{N}}}'+{{\dot{\varphi }}}' Q+{\varphi }' {\dot{Q}}-{\dot{\varphi }} q} \right) \vec {e}_1 +\left( {{\dot{Q}}'-{{\dot{\varphi }}}' N-{\varphi }'{\dot{N}}+{\dot{\varphi }} n} \right) \vec {e}_3. \end{aligned}$$

(20.2)

The latter relation follows from Eq. (20.1) by taking into account Eqs. (10), (11), and (13). Recall that both the equilibrium relations for the intermediate configuration, Eqs. (13) and (14), as well as the rate equilibrium relations, Eqs. (18) and (19), are referred to the same undeformed reference configuration. Particularly, when the intermediate configuration and the undeformed reference configuration do coincide, i.e. in the linear theory of rods, it follows that Eqs. (13) and (14) are trivially satisfied, because then there is $n=0$, $q=0$, $m=0$, $N=0$, $Q=0$, $M=0$, $\varLambda =1$, $\chi =0$, $\varphi =\varphi _0$, where $\varphi _0$ denotes the value of the angle $\varphi$ in the undeformed reference configuration. The rate form of the equilibrium relations, Eqs. (18) and (19), in this special case indeed yields the well-known equilibrium conditions of the linear theory of rods, see [1] and Ziegler [5].

3 Local virtual work relations

Since we intend to derive reciprocity relations later on, we here provide local virtual work relations fitting to the rate equilibrium conditions stated in Eqs. (18) and (19). This is performed by a scalar multiplication of Eq. (18) with a virtual displacement increment. In the following, virtual increments are indicated by underlined symbols, and they are understood as functions of the axial coordinate $s_0$ in the reference configuration again. These underlined virtual entities are assumed to correspond to an infinitesimal test deformation superimposed upon the same intermediate configuration introduced above, such that we are allowed to use superimposed dots also for the virtual entities. Hence, we obtain the local virtual work relation for the forces in the form

$$\begin{aligned} \dot{{\vec {R}}'}\cdot {\underline{\dot{\vec {r}}}}+\dot{\vec {p}}\cdot {\underline{\dot{\vec {r}}}}=\vec {0}. \end{aligned}$$

(21)

Now assume, for the moment being, that the entities are smooth enough at the place $s_0$, such that the product rule of differentiation can be applied to Eq. (21):

$$\begin{aligned} \left( {\dot{\vec {R}}\cdot {\underline{\dot{\vec {r}}}}} \right) ^{\prime }-\dot{\vec {R}}\cdot {{\underline{\dot{\vec {r}}}}}'+\dot{\vec {p}}\cdot {\underline{\dot{\vec {r}}}}=0. \end{aligned}$$

(22)

The increment of the virtual axial deformation gradient vector ${\vec {r}}'$ follows by time-wise differentiation of Eq. (12):

$$\begin{aligned} {{\underline{\dot{\vec {r}}}}}'=\left( {\dot{{\underline{\varLambda }}} \cos \chi -\varLambda {{\dot{\underline{\chi }}}} \sin \chi -\varLambda \dot{{\underline{\varphi }}}\sin \chi } \right) \vec {e}_1 -\left( {\dot{{\underline{\varLambda }}} \sin \chi +\varLambda {\dot{\underline{\chi }}}\cos \chi +\varLambda \dot{{\underline{\varphi }}}\cos \chi } \right) \vec {e}_3. \end{aligned}$$

(23)

Substituting Eqs. (20) and (23) into (22) yields

$$\begin{aligned}&\left( {\dot{\vec {R}}\cdot {\underline{\dot{\vec {r}}}}} \right) ^{\prime }- Q\left( {{\dot{\varphi }} \dot{{\underline{\varLambda }}} \cos \chi -\varLambda \dot{\varphi }\left( { {{\dot{\underline{\chi }}}}+ \dot{{\underline{\varphi }}}} \right) \sin \chi } \right) -N \left( {{\dot{\varphi }} \dot{{\underline{\varLambda }}} \sin \chi +\varLambda {\dot{\varphi }}\left( { {{\dot{\underline{\chi }}}}+ \dot{{\underline{\varphi }}}} \right) \cos \chi } \right) \nonumber \\&\quad +\varLambda \left( {{\dot{Q}}\left( { {{\dot{\underline{\chi }}}}+ \dot{{\underline{\varphi }}}} \right) \cos \chi +{\dot{N}}\left( { {{\dot{\underline{\chi }}}}+ \dot{{\underline{\varphi }}}} \right) \sin \chi } \right) +\left( {{\dot{Q}} \sin \chi -{\dot{N}} \cos \chi } \right) \dot{{\underline{\varLambda }}}+\dot{\vec {p}}\cdot {\underline{\dot{\vec {r}}}}=0. \end{aligned}$$

(24)

Similarly, multiplying the incremental equilibrium relation for the moment, Eq. (19), with a virtual rate of the rotation angle $\dot{{\underline{\varphi }}}$ yields

$$\begin{aligned}&\left( {{\dot{M}} \dot{{\underline{\varphi }}}} \right) ^{\prime }-{\dot{M}} {\dot{{\underline{\varphi }}}}'-Q \left( {{\dot{\varLambda }} \dot{{\underline{\varphi } }}\cos \chi -\varLambda {\dot{\chi }} \dot{{\underline{\varphi } }} \sin \chi } \right) -N\left( {{\dot{\varLambda }} \dot{{\underline{\varphi }}}\sin \chi +\varLambda {\dot{\chi }}\dot{{\underline{\varphi }}}\cos \chi } \right) \nonumber \\&\quad -\varLambda \left( { {\dot{Q}} \dot{{\underline{\varphi }}}\cos \chi +{\dot{N}} \dot{{\underline{\varphi }}}\sin \chi } \right) +{\dot{m}} \dot{{\underline{\varphi }}}=0. \end{aligned}$$

(25)

Adding Eqs. (24) and (25), we obtain the local relation of virtual work of the incremental external and internal forces and moments done with respect to the virtual incremental test deformations as

$$\begin{aligned}&\left( {\dot{\vec {R}}\cdot {\underline{\dot{\vec {r}}}}+{\dot{M}} \dot{{\underline{\varphi }}}} \right) ^{\prime }+ \left( {{\dot{Q}} \sin \chi -{\dot{N}}\cos \chi } \right) \dot{{\underline{\varLambda }}}- {\dot{M}} {\dot{{\underline{\varphi }}}}' \nonumber \\&\quad - Q\left( {\left( {{\dot{\varphi }} \dot{{\underline{\varLambda }}}+\dot{{\underline{\varphi }}} {\dot{\varLambda }}} \right) \cos \chi -\varLambda \left( {{\dot{\varphi }} {{\dot{\underline{\chi }}}} + {\dot{\chi }} \dot{{\underline{\varphi }}} + {\dot{\varphi }} \dot{{\underline{\varphi }}}} \right) \sin \chi } \right) \nonumber \\&\quad -N \left( {\varLambda \left( {{\dot{\varphi }} {{\dot{\underline{\chi }}}}+\dot{\chi } \dot{{\underline{\varphi }}}+{\dot{\varphi }} \dot{{\underline{\varphi }}}} \right) \cos \chi +\left( {{\dot{\varphi }} \dot{{\underline{\varLambda }}} +{\dot{\varLambda }} \dot{{\underline{\varphi }}}} \right) \sin \chi } \right) \nonumber \\&\quad +\varLambda \left( {{\dot{Q}} {{\dot{\underline{\chi }}}}\cos \chi +\dot{N}{{\dot{\underline{\chi }}}} \sin \chi } \right) \nonumber \\&\quad +\dot{\vec {p}}\cdot {\underline{\dot{\vec {r}}}}+{\dot{m}} \dot{{\underline{\varphi }}}=0. \end{aligned}$$

(26)

This relation can be further simplified by utilizing generalized strain measures that were introduced by Reissner [2]. These measures consist of a generalized extensional strain,

$$\begin{aligned} \varepsilon =\varLambda \cos \chi -1,\quad {\dot{\varepsilon }}=\dot{\varLambda } \cos \chi -\varLambda {\dot{\chi }} \sin \chi , \end{aligned}$$

(27)

a generalized shear strain,

$$\begin{aligned} \gamma =-\,\varLambda \sin \chi ,\quad {\dot{\gamma }}=-\,{\dot{\varLambda }} \sin \chi -\varLambda {\dot{\chi }} \cos \chi , \end{aligned}$$

(28)

and a generalized bending strain,

$$\begin{aligned} \kappa ={\varphi }',\quad {\dot{\kappa }}={\dot{\varphi }'}. \end{aligned}$$

(29)

Substituting the deformation rates in Eqs. (27) and (28) into (26), one obtains the reduced form

$$\begin{aligned}&\left( {\dot{\vec {R}}\cdot {\underline{\dot{\vec {r}}}}+{\dot{M}} \dot{{\underline{\varphi } }}} \right) ^{\prime }- {\dot{Q}} {{\dot{\underline{\gamma }}}}-{\dot{N}} {\dot{\underline{\varepsilon }}} - {\dot{M}} {\dot{{\underline{\varphi }}}}'- Q\left( {\left( {\dot{\varphi } \dot{{\underline{\varLambda }}}+\dot{{\varphi }} {\dot{\varLambda }}} \right) \cos \chi -\varLambda \left( {{\dot{\varphi }} {{\dot{\underline{\chi }}}} + \dot{{\underline{\varphi }}} {\dot{\chi }}+ {\dot{\varphi }} \dot{{\underline{\varphi }}}} \right) \sin \chi } \right) \nonumber \\&\quad -N \left( {\varLambda \left( {{\dot{\varphi }} {{\dot{\underline{\chi }}}}+\dot{{\underline{\varphi }}} {\dot{\chi }}+{\dot{\varphi }} \dot{{\underline{\varphi }}}} \right) \cos \chi +\left( {{\dot{\varphi }} \dot{{\underline{\varLambda }}} +\dot{{\underline{\varphi }}} \dot{\varLambda }} \right) \sin \chi } \right) +\dot{\vec {p}}\cdot {\underline{\dot{\vec {r}}}}+{\dot{m}} \dot{{\underline{\varphi }}}=0. \end{aligned}$$

(30)

4 Local and global universal reciprocity relations

We now consider the underlined virtual deformation quantities to correspond to a set of virtual internal and external forces and moments. The virtual forces and moments are designated by corresponding underlined symbols, and they are considered to produce a state of equilibrium, too, likewise to the original forces and moments. We are thus allowed to interchange the roles of the underlined and non-underlined quantities in Eq. (30), which yields

$$\begin{aligned}&\left( {{{\underline{\dot{\vec {R}}}}}\cdot \dot{\vec {r}}+{{\dot{\underline{M}}}} \dot{\varphi }} \right) ^{\prime }- {{\dot{\underline{Q}}}} {\dot{\gamma }}-{{\dot{\underline{N}}}} \dot{\varepsilon } - {{\dot{\underline{M}}}} {{\dot{\varphi }}}'- Q\left( {\left( {\dot{{\underline{\varphi }}} {\dot{\varLambda }}+{\dot{\varphi }} \dot{{\underline{\varLambda }}}} \right) \cos \chi -\varLambda \left( {\dot{{\underline{\varphi }}} {\dot{\chi }}+{\dot{\varphi }}{{\dot{\underline{\chi }}}} + \dot{{\underline{\varphi }}} {\dot{\varphi }}} \right) \sin \chi } \right) \nonumber \\&\quad -N \left( {\varLambda \left( {\dot{{\underline{\varphi }}} {\dot{\chi }}+\dot{\varphi } {{\dot{\underline{\chi }}}}+\dot{{\underline{\varphi }}} {\dot{\varphi }}} \right) \cos \chi +\left( {\dot{{\underline{\varphi }}} {\dot{\varLambda }}+{\dot{\varphi }} \dot{{\underline{\varLambda }}}} \right) \sin \chi } \right) +{{\underline{\dot{\vec {p}}}}}\cdot \dot{\vec {r}}+{{\dot{\underline{m}}}} {\dot{\varphi }}=0. \end{aligned}$$

(31)

The relation in Eq. (31) represents the local virtual work of the underlined virtual forces and moments done upon the non-underlined incremental deformations, which we denote as original ones in the following, while underlined quantities will be called virtual ones. Subtracting Eq. (31) from Eq. (30) yields the following universal local reciprocity relation:

$$\begin{aligned}&\left( {\dot{\vec {R}}\cdot {\underline{\dot{\vec {r}}}}+{\dot{M}} \dot{{\underline{\varphi } }}} \right) ^{\prime }- {\dot{Q}} {{\dot{\underline{\gamma }}}}-{\dot{N}} {\dot{\underline{\varepsilon }}} - {\dot{M}} {\dot{{\underline{\varphi }}}}'+\dot{\vec {p}}\cdot {\underline{\dot{\vec {r}}}}+{\dot{m}} \dot{{\underline{\varphi }}} \nonumber \\&\quad =\left( {{{\underline{\dot{\vec {R}}}}}\cdot \dot{\vec {r}}+{{\dot{\underline{M}}}} {\dot{\varphi }}} \right) ^{\prime }- {{\dot{\underline{Q}}}} {\dot{\gamma }}-{\dot{\underline{N}}} {\dot{\varepsilon }}- {{\dot{\underline{M}}}}{{\dot{\varphi }}}'+{{\underline{\dot{\vec {p}}}}}\cdot \dot{\vec {r}}+{{\dot{\underline{m}}}} {\dot{\varphi }}. \end{aligned}$$

(32)

We call this relation as universal, since it must hold for any constitutive relation of the rod under consideration. Note that Eq. (31) also nicely reflects the fact that Reissner’s generalized strain measures, see Eqs. (27)–(29), are work conjugate to the internal forces and moments.

We now integrate over the rod segment under consideration, over the region $0\le s_0 \le l_0$ in the reference configuration. Assuming that the original incremental forces, moments, and deformations may suffer jumps at the place $s_0 =a_0$, while the virtual entities may jump at $s_0 ={a}_0$, integration of the bracketed terms at both sides of Eq. (32), the differentials of which are indicated by primes, must be performed piecewise. Eventually, the following global universal reciprocity relation including jumps of static and/or kinematic quantities is obtained:

$$\begin{aligned}&\int _{s_0 =0}^{s_0 =l_0 } {\left( {\dot{\vec {p}}\cdot {\underline{\dot{\vec {r}}}}+{\dot{m}} \dot{{\underline{\varphi }}}} \right) \hbox {d}s_0 } -\left. {\left( {\llbracket {\dot{\vec {R}}} \rrbracket \cdot {\underline{\dot{\vec {r}}}}+\llbracket {{\dot{M}}} \rrbracket \dot{{\underline{\varphi }}}} \right) } \right| _{s_0 =a_0 } -\left. {\left( {\dot{\vec {R}}\cdot \llbracket {{\underline{\dot{\vec {r}}}}} \rrbracket +{\dot{M}} \llbracket {\dot{{\underline{\varphi }}}} \rrbracket } \right) } \right| _{s_0 ={\underline{a}}_0} \nonumber \\&\quad \quad -\int _{s_0 =0}^{s_0 =l_0 } {\left( {{\dot{Q}} {\dot{\underline{\gamma }}}+{\dot{N}} {{\dot{\underline{\varepsilon }}}} + {\dot{M}} {\dot{{\underline{\varphi }}}}'} \right) \hbox {d}s_0 } \nonumber \\&\quad =\int _{s_0 =0}^{s_0 =l_0 } {\left( {{{\underline{\dot{\vec {p}}}}}\cdot \dot{\vec {r}}+{{\dot{\underline{m}}}} {\dot{\varphi }}} \right) \hbox {d}s_0 } -\left. {\left( {\llbracket {{{\underline{\dot{\vec {R}}}}}} \rrbracket \cdot \dot{\vec {r}}+\llbracket {{{\dot{\underline{M}}}}} \rrbracket {\dot{\varphi }}} \right) } \right| _{s_0 ={\underline{a}}_0 } -\left. {\left( {{{\underline{\dot{\vec {R}}}}}\cdot \llbracket {\dot{\vec {r}}} \rrbracket +{{\dot{\underline{M}}}} \llbracket {\dot{\varphi }} \rrbracket } \right) } \right| _{s_0 =a_0 }\nonumber \\&\quad \quad -\int _{s_0 =0}^{s_0 =l_0 } {\left( {{{\dot{\underline{Q}}}} \dot{\gamma }+{{\dot{\underline{N}}}} {\dot{\varepsilon }}+ {{\dot{\underline{M}}}} {{\dot{\varphi }}}'} \right) \hbox {d}s_0 }. \end{aligned}$$

(33)

Jumps are indicated by double brackets,

$$\begin{aligned} \left. {\llbracket f \rrbracket } \right| _{s_0 =a_0 } =\mathop {\lim }\limits _{\varepsilon \rightarrow 0} \left( {\left. f \right| _{s_0 =a_0 +\varepsilon } -\left. f \right| _{s_0 =a_0 -\varepsilon } } \right) . \end{aligned}$$

(34)

In deriving Eq. (33), it has been assumed with little loss of generality, but for the sake of brevity that

$$\begin{aligned} \left. {\left( {\dot{\vec {R}}\cdot {\underline{\dot{\vec {r}}}}+{\dot{M}} \dot{{\underline{\varphi }}}} \right) } \right| _{s_0 =0}^{s_0 =l_0 } =\left. {\left( {{{\underline{\dot{\vec {R}}}}}\cdot \dot{\vec {r}}+{{\dot{\underline{M}}}} {\dot{\varphi }}} \right) } \right| _{s_0 =0}^{s_0 =l_0 }. \end{aligned}$$

(35)

This relation is trivially satisfied for classical homogeneous boundary conditions at the rod ends, e.g. at a clamped end, kinematic quantities do vanish. Moreover, note that the amounts of the jumps in Eq. (33) usually can be taken as known, because they correspond to the following static and kinematic relations of jump, respectively:

$$\begin{aligned}&\left. {\llbracket {\dot{\vec {R}}} \rrbracket } \right| _{s_0 =a_0} +\dot{\vec {F}}_{imp} =\vec {0},\quad \left. {\llbracket {{{\underline{\dot{\vec {R}}}}}} \rrbracket } \right| _{s_0 ={\underline{a}}_0 } +\dot{{\vec {\underline{F}}}}_{imp} =\vec {0}, \end{aligned}$$

(36)

$$\begin{aligned}&\left. {\llbracket {{\dot{M}}} \rrbracket } \right| _{s_0 =a_0 } +{\dot{M}}_{imp} =0,\quad \left. {\llbracket {{{\dot{\underline{M}}}}} \rrbracket } \right| _{s_0 ={\underline{a}}_0 } +\dot{{\underline{M}}}_{imp} =0, \end{aligned}$$

(37)

$$\begin{aligned}&\left. {\llbracket {\dot{\vec {r}}} \rrbracket } \right| _{s_0 =a_0 } -\dot{\vec {\varDelta }}_{imp} =\vec {0},\quad \left. {\llbracket {{{\underline{\dot{\vec {r}}}}}} \rrbracket } \right| _{s_0 ={\underline{a}}_0 } -\dot{{\vec {\underline{\varDelta }}}}_{imp} =\vec {0}, \end{aligned}$$

(38)

$$\begin{aligned}&\left. {{{\dot{\varphi }}}} \right| _{s_0 =a_0 } -\dot{\theta }_{imp} =0,\quad \left. {\llbracket {{{\dot{\underline{\varphi }}}}} \rrbracket } \right| _{s_0 ={\underline{a}}_0 } -\dot{{\underline{\theta }}}_{imp} =0. \end{aligned}$$

(39)

The index imp in Eqs. (36)–(39) refers to an imposed quantity.

5 Global reciprocity relations for hyperelastic rod

Following Reissner [2], the constitutive relations of an elastic rod can be formulated as functions of the generalized strains stated in Eqs. (27)–(29), from which their rate forms follow by differentiation with respect to time:

$$\begin{aligned} Q= & {} Q\left( {\varepsilon ,\;{\varphi }',\;\gamma ,\gamma _e } \right) :\quad {\dot{Q}}=\frac{\partial Q}{\partial \varepsilon } \dot{\varepsilon }+\frac{\partial Q}{\partial {\varphi }'} {\dot{\varphi }'}+\frac{\partial Q}{\partial \gamma } \dot{\gamma }+\frac{\partial Q}{\partial \gamma _e } {\dot{\gamma }}_e, \end{aligned}$$

(40)

$$\begin{aligned} N= & {} N\left( {\varepsilon ,\;{\varphi }',\;\gamma ,\varepsilon _e } \right) :\quad {\dot{N}}=\frac{\partial N}{\partial \varepsilon } \dot{\varepsilon }+\frac{\partial N}{\partial {\varphi }'} {\dot{\varphi }'}+\frac{\partial N}{\partial \gamma } \dot{\gamma }+\frac{\partial N}{\partial \varepsilon _e } {\dot{\varepsilon }}_e, \end{aligned}$$

(41)

$$\begin{aligned} M= & {} M\left( {\varepsilon ,\;{\varphi }',\;\gamma , \varepsilon _e ,\;{\varphi }'_e ,\;\gamma _e } \right) :\quad {\dot{M}}=\frac{\partial M}{\partial \varepsilon } {\dot{\varepsilon }}+\frac{\partial M}{\partial {\varphi }'} {\dot{\varphi }'}+\frac{\partial M}{\partial \gamma } {\dot{\gamma }}+\frac{\partial M}{\partial {\varphi }'_e } {\dot{\varphi }'}_e. \end{aligned}$$

(42)

In Eqs. (40)–(42), we also have introduced generalized eigenstrains $\varepsilon _e$, $\gamma _e$, and ${\varphi }'_e$, as well as their rates, these eigenstrains being taken as known in the following. For the sake of simplicity, we assume forces and moments to depend on the respective generalized eigenstrains only, see the last terms in Eqs. (40)–(42). Now, for hyperelastic rods, certain necessary and sufficient integrability conditions must be satisfied in order that the existence of a potential function can be guaranteed. These conditions read:

$$\begin{aligned} \frac{\partial Q}{\partial \varepsilon }=\frac{\partial N}{\partial \gamma },\quad \frac{\partial Q}{\partial {\varphi }'}=\frac{\partial M}{\partial \gamma },\quad \frac{\partial N}{\partial {\varphi }'}=\frac{\partial M}{\partial \varepsilon }. \end{aligned}$$

(43)

For rods rigid in shear, where $\gamma =0$ and ${\dot{\gamma }}=0$, see DaDeppo [4]. Relations analogous to Eqs. (40)–(43) also hold for the virtual (underlined) quantities; however, we subsequently consider eigenstrains to be absent in the virtual problem:

$$\begin{aligned} {\underline{\varepsilon }}_e =0,\;{{\underline{\varphi }}'}_e =0,\;{\underline{\gamma }}_e =0. \end{aligned}$$

(44)

Using Eqs. (40)–(44), one obtains

$$\begin{aligned} {\dot{Q}} {{\dot{\underline{\gamma }}}}+{\dot{N}} {{\dot{\underline{\varepsilon }}}} + {\dot{M}} {\dot{{\underline{\varphi } }}}'-{{\dot{\underline{Q}}}} {\dot{\gamma }}-{{\dot{\underline{N}}}} \dot{\varepsilon } -{{\dot{\underline{M}}}} {\dot{\varphi }'}=\frac{\partial Q}{\partial \gamma _e } {\dot{\gamma }} {\dot{\underline{\gamma }}}+\frac{\partial N}{\partial \varepsilon _e } {\dot{\varepsilon }}_e {{\dot{\underline{\varepsilon }}}} +\frac{\partial M}{\partial {\varphi }'_e } {\dot{\varphi }'}_e{\dot{{\underline{\varphi }}}}'. \end{aligned}$$

(45)

Substituting Eq. (45) into the universal global relation of reciprocity, Eq. (33), and considering Eq. (35), yields the following generalized reciprocity relation for hyperelastic rods in the presence of rates of eigenstrain in the original problem:

$$\begin{aligned}&\int _{s_0 =0}^{s_0 =l_0 } {\left( {\dot{\vec {p}}\cdot {\underline{\dot{\vec {r}}}}+{\dot{m}} \dot{{\underline{\varphi }}}} \right) \hbox {d}s_0 } -\left. {\left( {\llbracket {\dot{\vec {R}}} \rrbracket \cdot {\underline{\dot{\vec {r}}}}+\llbracket {{\dot{M}}} \rrbracket \dot{{\underline{\varphi }}}} \right) } \right| _{s_0 =a_0 } -\left. {\left( {\dot{\vec {R}}\cdot \llbracket {{\underline{\dot{\vec {r}}}}} \rrbracket +{\dot{M}} \llbracket {\dot{{\underline{\varphi }}}} \rrbracket } \right) } \right| _{s_0 ={\underline{a}}_0}\nonumber \\&\quad \quad -\int _{s_0 =0}^{s_0 =l_0 } {\left( { \frac{\partial Q}{\partial \gamma _e } {\dot{\gamma }}_e {\dot{\underline{\gamma }}}+\frac{\partial N}{\partial \varepsilon _e } {\dot{\varepsilon }}_e {{\dot{\underline{\varepsilon }}}} + \frac{\partial M}{\partial {{\varphi }}'_e } {\dot{\varphi }'}_e {\dot{{\underline{\varphi }}}}'} \right) \hbox {d}s_0 } \nonumber \\&\quad =\int _{s_0 =0}^{s_0 =l_0 } {\left( {{{\underline{\dot{\vec {p}}}}}\cdot \dot{\vec {r}}+{{\dot{\underline{m}}}} {\dot{\varphi }}} \right) \hbox {d}s_0 } -\left. {\left( {\llbracket {{{\underline{\dot{\vec {R}}}}}} \rrbracket \cdot \dot{\vec {r}}+\llbracket {{{\dot{\underline{M}}}}} \rrbracket {\dot{\varphi }}} \right) } \right| _{s_0 ={\underline{a}}_0 } -\left. {\left( {{{\underline{\dot{\vec {R}}}}}\cdot \llbracket {\dot{\vec {r}}} \rrbracket +{{\dot{\underline{M}}}} \llbracket {\dot{\varphi }} \rrbracket } \right) } \right| _{s_0 =a_0 }. \end{aligned}$$

(46)

As will be discussed subsequently, this relation includes and extends reciprocity relations known from the linear theory of rods to the case of infinitesimal deformations superimposed upon possibly large, but infinitesimally superstable deformations of rods. A main result of the present paper is that the form of these reciprocity relations is the same in both, the linear theory of rods (small deformations from an undeformed reference configuration) and in the theory of small deformations from an intermediate state with a possibly large deformation with respect to the reference state. In the latter case, the static and kinematic rates of course do depend on the deformation of the intermediate state. To the best knowledge of the present author, the combined presence of kinematic jumps and eigenstrains in reciprocity relations yields a novel formulation also with respect to the linear theory of hyperelastic rods.

5.1 Betti’s reciprocal theorem

Assuming eigenstrains as well as any jumps to be absent, from Eq. (46) we obtain the celebrated reciprocity theorem of Betti, see [5] for the linear theory, and Da Deppo [4] for infinitesimal deformations superimposed on finite deformations:

$$\begin{aligned} \int _{s_0 =0}^{s_0 =l_0 } {\left( {\dot{\vec {p}}\cdot {\underline{\dot{\vec {r}}}}+{\dot{m}} \dot{{\underline{\varphi }}}} \right) \hbox {d}s_0 } =\int _{s_0 =0}^{s_0 =l_0 } {\left( {{{\underline{\dot{\vec {p}}}}}\cdot \dot{\vec {r}}+{{\dot{\underline{m}}}} {\dot{\varphi }}} \right) \hbox {d}s_0 }. \end{aligned}$$

(47)

The relation stated in Eq. (46) extends the result of DaDeppo [4] for rods rigid in shear to shear-deformable rods.

5.2 Maxwell’s reciprocal theorem

Considering single forces in both, the original and the virtual problem, Eqs. (36) and (37), Eq. (46) delivers Maxwell’s well-known reciprocity theorem, see [5] for the linear theory:

$$\begin{aligned} \left. {\left( {\llbracket {\dot{\vec {R}}} \rrbracket \cdot {\underline{\dot{\vec {r}}}}+\llbracket {{\dot{M}}} \rrbracket \dot{{\underline{\varphi } }}} \right) } \right| _{s_0 =a_0 } =\left. {\left( {\llbracket {{{\underline{\dot{\vec {R}}}}}} \rrbracket \cdot \dot{\vec {r}}+\llbracket {{{\dot{\underline{M}}}}} \rrbracket {\dot{\varphi }}} \right) } \right| _{s_0 ={\underline{a}}_0 }. \end{aligned}$$

(48)

5.3 Reciprocity theorem dating back to Land

We now study the presence of jumps of the static and kinematic entities in the absence of eigenstrains and distributed forces and moments in Eq. (46). One possible case is the presence of static entities suffering jumps in the original problem and kinematic entities that jump in the virtual one. This yields:

$$\begin{aligned} \left. {\left( {\llbracket {\dot{\vec {R}}} \rrbracket \cdot {\underline{\dot{\vec {r}}}}+\llbracket {{\dot{M}}} \rrbracket \dot{{\underline{\varphi }}}} \right) } \right| _{s_0 =a_0 } =-\left. {\left( {\dot{\vec {R}}\cdot \llbracket {{\underline{\dot{\vec {r}}}}} \rrbracket +{\dot{M}} \llbracket {\dot{{\underline{\varphi }}}} \rrbracket } \right) } \right| _{s_0 ={\underline{a}}_0}. \end{aligned}$$

(49)

In the linear theory, such a relation is known as the reciprocity theorem of Land. We refer to the book of Kurrent [6], who deserves the merit of bringing back this theorem to the attention of a wider audience.

5.4 Extension of Maysel’s formula

Consider the case of jumps being present in the static entities of the virtual problem, and of eigenstrains being present in the original problem in Eq. (46). One then obtains:

$$\begin{aligned} \left. {\left( {\llbracket {{{\underline{\dot{\vec {R}}}}}} \rrbracket \cdot \dot{\vec {r}}+\llbracket {{{\dot{\underline{M}}}}} \rrbracket {\dot{\varphi }}} \right) } \right| _{s_0 ={\underline{a}}_0 } =\quad \int _{s_0 =0}^{s_0 =l_0 } {\left( { \frac{\partial Q}{\partial \gamma _e } {\dot{\gamma }}_e {\dot{\underline{\gamma }}}+\frac{\partial N}{\partial \varepsilon _e } {\dot{\varepsilon }}_e {{\dot{\underline{\varepsilon }}}} + \frac{\partial M}{\partial {\varphi }'_e } {\dot{\varphi }'}_e {\dot{{\underline{\varphi }}}}'} \right) \hbox {d}s_0 }. \end{aligned}$$

(50)

Practically, this means that specific kinematic entities, located at $s_0 ={\underline{a}}_0$ and produced by eigenstrains in the original problem, can be obtained by integration along the rod, once the solution of the virtual problem is known due to jumps of the work-conjugated static quantities, also applied at $s_0 ={\underline{a}}_0$. This technique is known as Maysel’s formula in the linear theory of thermal eigenstrains, see Ziegler and Irschik [7]. See Irschik et al. [8] for the finite strain context, and Irschik and Pichler [9] for small vibrations superimposed upon large static deformations of piezoelastic bodies.

5.5 An extension of Maysel’s formula motivated by the theorem of Land

We finally combine Maysel’s formula, Eq. (50), with the Land-type reciprocity theorem, Eq. (48). This means to consider jumps of the kinematic entities in the virtual problem, and to account for the presence of eigenstrains in the original problem. We then obtain from Eq. (46):

$$\begin{aligned} \left. {\left( {\dot{\vec {R}}\cdot \llbracket {{\underline{\dot{\vec {r}}}}} \rrbracket +{\dot{M}} \llbracket {\dot{{\underline{\varphi }}}} \rrbracket } \right) } \right| _{s_0 ={\underline{a}}_0 } =-\int _{s_0 =0}^{s_0 =l_0 } {\left( { \frac{\partial Q}{\partial \gamma _e } {\dot{\gamma }}_e{{\dot{\underline{\gamma }}}}+\frac{\partial N}{\partial \varepsilon _e } {\dot{\varepsilon }}_e {\dot{\underline{\varepsilon } }} + \frac{\partial M}{\partial {\varphi }'_e } {\dot{\varphi }'}_e {\dot{{\underline{\varphi } }}}'} \right) \hbox {d}s_0 }. \end{aligned}$$

(51)

This allows computing internal forces and moments due to the eigenstrains, when the solution of the virtual problem due to the jumps of the kinetic entities is known. To the best knowledge of the present author, Eq. (51) represents a novel extension of Maysel’s procedure, not only with respect to the case of infinitesimal deformations superimposed upon a finite strain, but also in the framework of the purely linear theory.

6 Example problem

For an exemplary confirmation of the validity of our above results, we consider the case of an initially straight beam, the axial coordinate in the undeformed configuration being denoted as $s_0 =x$, where $0\le x\le l_0 =l$. The rod is taken as simply supported and axially movable at its left end, in $x=0$, while it is clamped and fixed at the right end, in $x=l$. For the intermediate configuration, we consider an external moment $M_0$ and an external axial force $R_{x0}$ to be applied at $x=0$, see Fig. 2.

Fig. 2

Undeformed and intermediate reference configurations of the example problem

We now assume imposed distributed forces and moments to be absent, where we first formulate relations for the intermediate configuration. The local equilibrium relations, Eqs. (13) and (14), now read

$$\begin{aligned}&{N}'+{\varphi }' Q=0, \end{aligned}$$

(52)

$$\begin{aligned}&{Q}'-{\varphi }' N=0, \end{aligned}$$

(53)

$$\begin{aligned}&{M}'-\varLambda \left( {Q \cos \chi +N\sin \chi } \right) =0. \end{aligned}$$

(54)

We need to introduce constitutive hyperelastic relations, which, for the sake of simplicity, are taken as linear functions of Reissner’s generalized strains, Eqs. (27)–(29), see also [1, 2],

$$\begin{aligned}&N=EA \varepsilon =EA \left( {\varLambda \cos \chi -1} \right) , \end{aligned}$$

(55)

$$\begin{aligned}&Q=kGA \gamma =kGA \varLambda \sin \chi , \end{aligned}$$

(56)

$$\begin{aligned}&M=EI \kappa =EI {\varphi }'. \end{aligned}$$

(57)

In accordance with a frequent notation in structural mechanics, EI denotes the bending stiffness, EA is the tensile stiffness, and kGA stands for the shear stiffness, k being the shear factor, and E denoting Young’s modulus. The cross-sectional area is A, and I denotes the cross-sectional moment of inertia.

The position vector of a point of the axis in the deformed configuration can be written as $\vec {r}=\left( {x+u} \right) \vec {e}_x +w \vec {e}_z$, the displacement gradient vector following to ${\vec {r}}'=\left( {1+{u}'} \right) \vec {e}_x +{w}' \vec {e}_z$. The axial displacement is denoted by u, and w is the deflection. In order to close the problem, the following kinematic relations are considered, which follow by representing the deformation gradient vector in the form of Eq. (12) in the global coordinate system, using Eqs. (4) and (5), and resolving for the displacement gradients:

$$\begin{aligned} {u}'= & {} \varLambda \left( {\cos \chi \cos \varphi -\sin \chi \sin \varphi } \right) -1, \end{aligned}$$

(58)

$$\begin{aligned} {w}'= & {} -\varLambda \left( {\cos \chi \sin \varphi +\sin \chi \cos \varphi } \right) . \end{aligned}$$

(59)

In order to eliminate the shear angle $\chi$ from the relations in Eqs. (54), (58) and (59), we utilize Eqs. (55) and (56), which yields

$$\begin{aligned}&{M}'-Q\left( {1+N \left( {\frac{1}{EA} +\frac{1}{k GA}} \right) } \right) =0, \end{aligned}$$

(60)

$$\begin{aligned}&{u}'=\left( {\frac{N}{EA}+1} \right) \cos \varphi -\frac{Q}{k GA}\sin \varphi -1, \end{aligned}$$

(61)

$$\begin{aligned}&{w}'=-\left( {\left( {\frac{N}{EA}+1} \right) \sin \varphi +\frac{Q}{k GA}\cos \varphi } \right) . \end{aligned}$$

(62)

We thus have arrived at a system of six first-order nonlinear ordinary differential equations, Eqs. (52), (53), (57), and (59)–(62), for determining the six unknown functions u, w, $\varphi$, N, Q, and M in the intermediate configuration. This set is accompanied by the following six boundary conditions:

$$\begin{aligned}&x=0:\quad w=0,\quad R_x =N \cos \varphi +Q \sin \varphi =R_{x0} ,\quad M=M_0 \end{aligned}$$

(63)

$$\begin{aligned}&x=l:\quad u=0,\quad w=0,\quad \varphi =0. \end{aligned}$$

(64)

The results enter the corresponding linear boundary-value problem for the superimposed infinitesimal deformations as known parameters, which however generally are non-constant.

For the original problem, the corresponding linear equilibrium relations follow in the absence of distributed imposed incremental forces and moments as, see Eqs. (13), (14), and (59):

$$\begin{aligned}&{{\dot{N}}}'+{{\dot{\varphi }}}' Q+{\varphi }' {\dot{Q}}=0, \end{aligned}$$

(65)

$$\begin{aligned}&{{\dot{Q}}}'-{{\dot{\varphi }}}' N-{\varphi }'{\dot{N}}=0, \end{aligned}$$

(66)

$$\begin{aligned}&\dot{{M}'}-{\dot{Q}}-\left( {Q {\dot{N}}+{\dot{Q}} N} \right) \left( {\frac{1}{EA}+\frac{1}{k GA}} \right) =0. \end{aligned}$$

(67)

Having eliminated the shear angle and its infinitesimal increment, the kinematic relations become, see also Eqs. (61) and (62):

$$\begin{aligned} {{\dot{u}}}'= & {} \frac{{\dot{N}}}{EA}\cos \varphi -\frac{{\dot{Q}}}{k GA}\sin \varphi -{\dot{\varphi }}\left( {\left( { \frac{N}{EA}+1} \right) \sin \varphi +\frac{Q}{k GA}\cos \varphi } \right) , \end{aligned}$$

(68)

$$\begin{aligned} {{\dot{w}}}'= & {} -\frac{{\dot{N}}}{EA}\sin \varphi -\frac{{\dot{Q}}}{k GA}\cos \varphi -{\dot{\varphi }}\left( {\left( {\frac{N}{EA}+1} \right) \cos \varphi -\frac{Q}{k GA}\sin \varphi } \right) . \end{aligned}$$

(69)

We particularly wish to obtain exemplary evidence for the correctness of the extended Maysel’s formula, Eq. (51). Subsequently, for the sake of brevity, we consider the presence of a bending-type generalized incremental eigenstrain ${{\dot{\varphi }}}'_e$ only. The corresponding linear constitutive bending relation is taken as

$$\begin{aligned} {\dot{M}}=EI\left( {{{\dot{\varphi }}}'-{{\dot{\varphi }}}'_e } \right) . \end{aligned}$$

(70)

The relations in Eqs. (65)–(70) represent a system of six first-order ordinary differential equations for the six incremental quantities ${\dot{u}}$, ${\dot{w}}$, ${\dot{\varphi }} , \dot{N}, {\dot{Q}}$ and ${\dot{M}}$ that are superimposed upon the intermediate configuration in the original problem, due to the generalized eigenstrain ${{\dot{\varphi }}}'_e$, sometimes also denoted as an imposed curvature. Since we consider the latter as the only loading here, the corresponding boundary conditions become, see Eqs. (63)–(64):

$$\begin{aligned} x= & {} 0:\quad {\dot{w}}=0,\;{\dot{R}}_x ={\dot{N}} \cos \varphi -N \dot{\varphi } \sin \varphi +{\dot{Q}} \sin \varphi +Q {\dot{\varphi }} \cos \varphi =0,\;{\dot{M}}=0, \end{aligned}$$

(71)

$$\begin{aligned} x= & {} l:\quad {\dot{u}}=0,{\dot{w}}=0,\;{\dot{\varphi }}=0. \end{aligned}$$

(72)

In order to exemplarily confirm the validity of Eq. (51), we consider the clamped end of the rod, i.e. we let ${\underline{a}}_0 \rightarrow l$, at which place we wish to compute the incremental clamping moment $\left. {{\dot{M}}} \right| _{x=l}$ due to ${{\dot{\varphi }}}'_e$. This means that we have to apply an imposed virtual negative cross-sectional rotation just left to the clamping end, in order to make $\left. {\llbracket {\dot{{\underline{\varphi }}}} \rrbracket } \right| _{x=l}$ positive. Hence, in order to set up the virtual problem, we use underlined symbols for the infinitesimal increments in Eqs. (65)–(72), where we set ${{\dot{\varphi }}}'_e =0$ in Eq. (70), and where, considering a unit jump $\left. {\llbracket {\dot{{\underline{\varphi }}}} \rrbracket } \right| _{x=l}=1$, we replace the boundary conditions in Eq. (72) by

$$\begin{aligned} x=l:\quad {{\dot{\underline{u}}}}=0,{{\dot{\underline{w}}}}=0,\;{{\dot{\underline{\varphi }}}}=-1. \end{aligned}$$

(73)

Note that, despite the virtual problem (the underlined quantities) is considered to represent an infinitesimal deformation, a unit jump of the cross-sectional rotation angle has been introduced. This is admissible due to the linearity of the problem at hand and is customary in linear structural mechanics, see e.g. [6].

The extended Maysel’s formula, Eq. (51), now specializes to

$$\begin{aligned} \left. {\left( {{\dot{M}} \llbracket {\dot{{\underline{\varphi }}}} \rrbracket } \right) } \right| _{x=l} =\left. {\dot{M}} \right| _{x=l} =-\int _{x=0}^{x=l} {\left( { \frac{\partial M}{\partial {\varphi }'_e } {\dot{\varphi }'}_e {\dot{{\underline{\varphi }}}}'} \right) \hbox {d}x}. \end{aligned}$$

(74)

Assuming that the constitutive behaviour is linear also for the intermediate configuration, and that, for the moment being, bending eigenstrains would be present, we find

$$\begin{aligned} M=EI\left( {{\varphi }'-{\varphi }'_e } \right) ,\quad \frac{\partial M}{\partial {\varphi }'_e }=-EI. \end{aligned}$$

(75)

This gives

$$\begin{aligned} \left. {{\dot{M}}} \right| _{x=l} =\int _{x=0}^{x=l} {\left( { EI {\dot{{\underline{\varphi }}}}'{\dot{\varphi }'}_e } \right) \hbox {d}x} =\int _{x=0}^{x=l} {\left( { \dot{{\underline{M}}} {\dot{\varphi }'}_e } \right) \hbox {d}x}. \end{aligned}$$

(76)

Assuming that the bending stiffness and the imposed curvature are both constant along the beam, $EI=\hbox {const.}$, ${\dot{\varphi }}_e ^{\prime }=\hbox {const.}$, Eq. (74) yields the alternative form, see Eq. (73):

$$\begin{aligned} {\dot{M}} _{x=l} =EI\;{\dot{\varphi }'}_e \int _{x=0}^{x=l} {{\dot{{\underline{\varphi }}}}' \hbox {d}x} =EI\;{\dot{\varphi }'}_e \left( {\left. {\dot{{\underline{\varphi }}}} \right| _{x=l} -\left. {\dot{{\underline{\varphi }}}} \right| _{x=0} } \right) =-EI\;{\dot{\varphi }'}_e \left( {1+\left. {\dot{{\underline{\varphi }}}} \right| _{x=0} } \right) . \end{aligned}$$

(77)

This form can be easily evaluated once $\left. {\dot{{\underline{\varphi }}}} \right| _{x=0}$ has been obtained as solution of the virtual problem.

For a validation, numerical solutions of the three exemplary boundary-value problems (the intermediate, the original, and the virtual problem) stated in Eqs. (52)–(73) have been obtained by means of the symbolic computer code Maple [10], version 2017. For the nonlinear intermediate problem, the command dsolve, together with the options numeric and output=listprocedure, was utilized. The numerically obtained point-wise results for the intermediate configuration were introduced into the Maple-formulations for the linear original and virtual problems via the additional option known=() in the command dsolve. Default settings of Maple [10] were used, e.g. concerning a selection of integration procedures. It turned out that, as long as the procedures did converge, results were obtained with a small computational effort, “just at fingertips”, despite the problems at hand appear to be comparatively involved. In our numerical computations, differences between the numerical outcomes of the original problem and of Eq. (77), the latter involving the virtual problem, remained comparatively small. For instance, we considered a thick rod of circular cross section with diameter $d=0.2\,\hbox {m}$, length $l=1\,\hbox {m}$, and Young’s modulus $E=100\,\hbox {GPa}$. Bending stiffness then is $EI=2.5\,\uppi \hbox {MPa}$, tensile stiffness is $EA=\uppi \hbox {MPa}$, and we set $kGA=0.5\,\uppi \hbox {MPa}$. For the boundary conditions of the intermediate problem, Eq. (63), the end moment was taken as $M_0 =10 \pi ^{2}\hbox {KNm}$, and an axial compressive force $R_{x0}$ was applied, which was 95% of the classical Euler buckling force for the problem at hand, not taking into account shear and extension, see e.g. [5]. Having obtained the solutions for the intermediate problem, Eqs. (52), (53), (57), and (59)–(64), the original problem in Eqs. (65)–(72) was solved directly for a unit incremental imposed curvature, ${\dot{\varphi }'}_e =1\,\hbox {m}^{-1}$. Afterwards, the solution of the virtual problem was computed and used to evaluate Eq. (77) for obtaining the bending moment $\left. {{\dot{M}} } \right| _{x=l}$ at the clamped end. The numerical algorithms implemented in Maple in our hands delivered a difference of 0.0525% between Eq. (77) and the outcome of the original problem in Eqs. (65)–(72). When the diameter of the beam was decreased to $d=0.01\,\hbox {m}$, this difference increased to 0.4203%. The following explanation has been provided:

As already mentioned, the above Land-type extension of Maysel’s formula in the context of an intermediate state with a large deformation, Eq. (51), appears to represent a novel contribution to the eigenstrain theory. Extended numerical studies, concerning initially curved beams and eigenstrain loadings that are more complex than the constant bending-type one acting on an initially straight beam, which has been treated in the above exemplary numerical study with respect to Eq. (77), will be published in a forthcoming paper.

Note, however, that analytic checks of the more general Eq. (76) are possible via exemplary results from the literature on initially straight beams with non-constant eigenstrain loadings, when the undeformed configuration and the intermediate configuration do coincide, i.e. in the purely linear case, assuming $M_0 =0$ and $R_{x0} =0.$ Consider again the case of a simply supported—clamped beam. Assume that the imposed curvature in the original problem is a box-type temperature difference between the upper and lower side of the beam,

$$\begin{aligned} {\dot{\varphi }'}_e =\frac{\gamma \left( {T_2 -T_1 } \right) }{t}H\left( {x-a} \right) . \end{aligned}$$

(78)

The Heaviside function is abbreviated by H. The symbols $T_1$ and $T_2$ denote the temperatures on the top and bottom surfaces, respectively, $\gamma$ is the coefficient of temperature expansion, and t stands for the thickness of the rod. This case is studied in Table 8.1: shear, moment, slope, and deflection formulas for elastic straight beams, Example 6c of Roark’s Formulas for Stress and Strain [11]. We are interested in the corresponding bending moment at $x=a$, where the Heaviside-box begins. From Table 8.1, Example 6c of [11], we learn that

$$\begin{aligned} \left. {M } \right| _{x=a} =-\frac{3}{2}\frac{ EI a}{l^{3}}\frac{\gamma \left( {T_2 -T_1 } \right) }{t}\left( {l^{2}-a^{2}} \right) . \end{aligned}$$

(79)

Superimposed dots are not needed in the present case. For a confirmation of Eq. (79), we analogously apply Eq. (76) to $x=a$:

$$\begin{aligned} M_{x=a} =\int _{x=0}^{x=l} {\left( { {\underline{M}} {\dot{\varphi }'}_e} \right) \hbox {d}x} =\frac{\gamma \left( {T_2 -T_1 } \right) }{t}\int _{x=a}^{x=l} {{\underline{M}} \hbox {d}x}. \end{aligned}$$

(80)

Recall that the virtual bending moment ${\underline{M}}$ denotes the bending moment due to a unit jump in the cross-sectional rotation that is applied at $x=a$:

$$\begin{aligned} \llbracket {\dot{\underline{\varphi }}} \rrbracket \rrbracket _{x=a} = \theta _0= 1. \end{aligned}$$

(81)

This case is treated in Table 8.1, Example 4c of [11], from which we obtain that

$$\begin{aligned} {\underline{M}}=-\frac{3 EI a x}{l^{3}}\theta _0 =-\frac{3 EI a x}{l^{3}}. \end{aligned}$$

(82)

Substituting Eq. (82) into Eq. (80) indeed yields Eq. (79). This result, despite it has been obtained in the framework of the linear structural theory of beams rigid in shear, should provide further evidence for the appropriateness of our above considerations.