Skip to main content
SpringerLink
Log in

Disturbed elastic fields in a circular 2D finite domain containing a circular inhomogeneity and a finite interfacial zone

  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

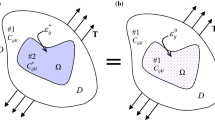
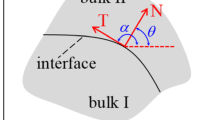
In order to take into account the effect of a finite interfacial zone between the inhomogeneity and matrix in an inhomogeneous representative volume element (RVE), analytical solutions for a 3-phase inclusion problem are needed. In this study, the primary focus is placed on a 3-phase concentric configuration for a 2D RVE, for which the exterior matrix is bounded and different elastic properties are assigned to the interior inclusion, interfacial zone and exterior matrix. In addition to the inhomogeneity induced by material mismatch, arbitrary uniform eigenstrains are allowed to occur independently within the interfacial zone and inclusion, respectively. In this study, the analytical solution is pursued via the complex potential method with the aid of 2 auxiliary potential functions. Based on the Sokhotski–Plemelj theorem, the complex potentials in each phase are constructed to account for the eigenstrains existing in the inclusion and the interfacial zone, as well as the imposed boundary conditions on the exterior matrix. The identification of the coefficients in the complex potential functions gives the analytical expressions for the disturbance induced by the inhomogeneity and eigenstrains. When compared with FEM simulations, a firm agreement is achieved for 3-phase concentric 2D finite domains. Furthermore, if the exterior matrix is extended to infinity, the obtained analytical solution reproduces the results given by Luo and Weng for uniform eigenstrain within the inclusion and by Markenscoff and Dundurs for uniform eigenstrain in the interfacial zone.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Eshelby J.D.: The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A 241, 376–396 (1957)

    Article  MATH  MathSciNet  Google Scholar 

  2. Eshelby J.D.: The elastic field outside an ellipsoidal inclusion. Proc. R. Soc. Lond. A 241, 376–396 (1959)

    Article  MathSciNet  Google Scholar 

  3. Nemat-Nasser S., Hori M.: Micromechanics: Overall Properties of Heterogeneous Materials, vol. 2. Elsevier, Amsterdam (1999)

    Google Scholar 

  4. Rodin G.J.: Eshelby’s inclusion problem for polygons and polyhedral. J. Mech. Phys. Solids 44, 1977–1995 (1996)

    Article  Google Scholar 

  5. Mori T., Tanaka K.: Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 21, 571–574 (1973)

    Article  Google Scholar 

  6. Hill R.: A self-consistent mechanics of composite materials. J. Mech. Phys. Solids 13, 213–222 (1965)

    Article  Google Scholar 

  7. Nozaki H., Taya M.: Elastic fields in a polygon-shaped inclusion with uniform eigenstrains. J. Appl. Mech. 64, 495–502 (1997)

    Article  MATH  Google Scholar 

  8. Nozaki H., Taya M.: Elastic fields in a polyhedral inclusion with uniform eigenstrains and related problems. J. Appl. Mech. 68, 441–452 (2001)

    Article  MATH  Google Scholar 

  9. Kuvshinov B.N.: Elastic and piezoelectric fields due to polyhedral inclusions. Int. J. Solids Struct. 45, 1352–1384 (2008)

    Article  MATH  Google Scholar 

  10. Li Q., Anderson P.M.: Dislocation-based modeling of the mechanical behavior of epitaxial metallic multilayer thin films. Acta Mater. 53, 1121–1134 (2005)

    Article  Google Scholar 

  11. Scrivener, K.L.: The microstructure of concrete. In: Skalny, J.P. (ed.) Material Science of Concrete, vol. 1, pp. 127–162. American Ceramic Society, Westerville (1989)

  12. Sun, Z.H., Garboczi, E.J., Shah, S.P.: Modeling the elastic properties of concrete composites: experiment, differential effective medium theory, and numerical simulation. Cem. Concr. Compos. 29, 22–38 (2006)

  13. Ryu I., Choi J.W., Cui Y., Nix W.D.: Size-dependent fracture of Si nanowire battery anodes. J. Mech. Phys. Solids 59, 1717–1730 (2011)

    Article  Google Scholar 

  14. Kim H., Cho J.: Superior lithium electroactive mesoporous Si@ Carbon core- shell nanowires for lithium battery anode material. Nano Lett. 8, 3688–3691 (2008)

    Article  Google Scholar 

  15. Luo H.A., Weng G.J.: On Eshelby’s inclusion problem in a three-phase spherically concentric solid, and a modification of Mori-Tanaka’s method. Mech. Mater. 6, 347–361 (1987)

    Article  Google Scholar 

  16. Luo H.A., Weng G.J.: On Eshelby’s S-tensor in a three-phase cylindrically concentric solid, and the elastic moduli of fiber-reinforced composites. Mech. Mater. 8, 77–88 (1989)

    Article  Google Scholar 

  17. Christensen R.M.: Mechanics of Composite Materials. Wiley, New York (1979)

    Google Scholar 

  18. Li G., Zhao Y., Pang S.-S.: Four-phase sphere modeling of effective bulk modulus of concrete. Cem. Concr. Res. 29, 839–845 (1999)

    Article  Google Scholar 

  19. Duan H.L., Jiao Y., Yi X., Huang Z.P., Wang J.: Solutions of inhomogeneity problems with graded shells and application to core–shell nanoparticles and composites. J. Mech. Phys. Solids 54, 1401–1425 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  20. Markenscoff X., Dundurs J.: Annular inhomogeneities with eigenstrain and interphase modeling. J. Mech. Phys. Solids 64, 468–482 (2014)

    Article  MathSciNet  Google Scholar 

  21. Ru C.Q.: A new method for an inhomogeneity with stepwise graded interphase under thermomechanical loadings. J. Elast. 56, 107–127 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  22. Ru C.Q.: Three-phase elliptical inclusions with internal uniform hydrostatic stresses. J. Mech. Phys. Solids 47, 259–273 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  23. Wang X., Gao X.-L.: On the uniform stress state inside an inclusion of arbitrary shape in a three-phase composite. Z. Angew. Math. Phys. 62, 1101–1116 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  24. Wang, X.: Eshelby’s inclusion and dislocation problems for an isotropic circular domain bonded to an anisotropic medium. Acta Mech., (in press) (2014)

  25. Li S., Sauer R.A., Wang G.: A circular inclusion in a finite domain I. The Dirichlet-Eshelby problem. Acta Mech. 179, 67–90 (2005)

    Article  MATH  Google Scholar 

  26. Wang G., Li S., Sauer R.: A circular inclusion in a finite domain II. The Neumann–Eshelby problem. Acta Mech. 179, 91–110 (2005)

    Article  Google Scholar 

  27. Li S., Sauer R.A., Wang G.: The Eshelby tensors in a finite spherical domain—part I: theoretical formulations. J. Appl. Mech. 74, 770–781 (2007)

    Article  MathSciNet  Google Scholar 

  28. Li S., Wang G., Sauer R.A.: The Eshelby tensors in a finite spherical domain—part II: applications to homogenization. J. Appl. Mech. 74, 784–797 (2007)

    Article  MathSciNet  Google Scholar 

  29. Timoshenko S.P., Goodier J.N.: Theory of Elasticity. McGraw-Hill, New York (1970)

    MATH  Google Scholar 

  30. Muskhelishvili N.I.: Some Basic Problems of the Mathematical Theory of Elasticity. Noordhoff, Groningen (1953)

    MATH  Google Scholar 

  31. Sherman, D.I.: On the problem of plane strain in non-homogeneous media. Non-homogeneity in Elasticity and Plasticity, pp. 3–20 (1959)

  32. Xu, X.F., Chen, X.: Stochastic homogenization of random elastic multi-phase composites and size quantification of representative volume element. Mech. Mater. 41, 174–186 (2009)

  33. Pan, C., Yu, Q.: Inclusion problem of a two-dimensional finite domain: the shape effect of matrix. Mech. Mater. 77, 86–97 (2014)

Download references

Author information

Authors and Affiliations

  1. Department of Civil and Environmental Engineering, University of Pittsburgh, Pittsburgh, PA, 15261, USA

    Chunlin Pan & Qiang Yu

Authors
  1. Chunlin Pan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qiang Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qiang Yu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pan, C., Yu, Q. Disturbed elastic fields in a circular 2D finite domain containing a circular inhomogeneity and a finite interfacial zone. Acta Mech 226, 1457–1470 (2015). https://doi.org/10.1007/s00707-014-1263-5

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-014-1263-5

Keywords

Search

Navigation