Summary
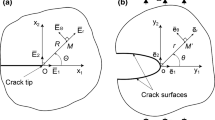
In this paper, we restore the already constructed approximate asymptotic solutions extracted in [10] concerning the HRR [1] strongly nonlinear fourth-order ordinary differential equation (ODE) for plane strain conditions in nonlinear elastic (plastic) fracture. It is proved that the above equation, for low strain hardening exponents (0 < N « 1), is reduced to a strongly nonlinear ODE of the second order. The method of the total differentials is used so that the last equation is reduced to Abels' equations of the second kind of the normal form, that can be analytically solved in parametric form. In addition, the case of rigid perfect-plasticity (N=0) is extensively investigated and several important results are extracted.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
J. R. Rice G. F. Rosengren (1968) ArticleTitlePlane strain deformation near a crack tip in a power-law hardening material J. Mech. Phys. Solids 16 1–12 Occurrence Handle10.1016/0022-5096(68)90013-6
J. W. Hutchinson (1968) ArticleTitleSingular behavior at the end of a tensile crack in a hardening material J. Mech. Phys. Solids 16 13–30 Occurrence Handle0166.20704 Occurrence Handle10.1016/0022-5096(68)90014-8
J. W. Hutchinson (1968) ArticleTitlePlane stress and strain field in a crack tip J. Mech. Phys. Solids 16 337–347 Occurrence Handle10.1016/0022-5096(68)90021-5
C. F. Shih (1974) ArticleTitleSmall-scale yielding analysis of mixed mode plane-strain crack problems ASTM STPP 500 187–210
J. R. Rice (1968) Mathematical analysis in the mechanics of fracture H. Liebowitz (Eds) Fracture, an advanced treatise, Vol. 2, Mathematical fundamentals Academic Press New York London 192–311
R. Hill (1950) The mathematical theory of plasticity Oxford University Press London
W. Prager P. G. Hodge (1968) Theory of perfectly plastic solids Dover New York
F. Absi (1984) ArticleTitleLa théorie de la plasticité et l' equilibre limite en mécanique des sols Ann. Inst. Tech. Batiment Travaux Publ. 421 66–123
J. Salençon (1974) Théorie de la plasticité pour les applications a la mécanique des sols Eyrolles Paris
D. E. Panayotounakos M. Markakis (1990) ArticleTitleClosed form solutions of the differential equations governing the plastic fracture field in a power-law hardening material with low strain-hardening exponent Ing.-Arch. 60 444–462 Occurrence Handle10.1007/BF00531255
Markakis, M.: Analytical techniques for solving nonlinear problems in mechanics of rigid bodies and fluid mechanics. P.H.D. Thesis, National Technical University of Athens, Greece.
A. D. Polyanin V. F. Zaitsev (1999) Handbook of exact solutions for ordinary differential equations CRC Press New York
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sotiropoulou, A., Panayotounakou, N. & Panayotounakos, D. Analytic parametric solutions for the HRR nonlinear elastic field with low hardening exponents. Acta Mechanica 183, 209–230 (2006). https://doi.org/10.1007/s00707-006-0315-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-006-0315-x