Skip to main content
SpringerLink
Log in

Complex potentials and integral equations for curved crack and curved rigid line problems in plane elasticity

  • Published:
Acta Mechanica Aims and scope Submit manuscript

Summary

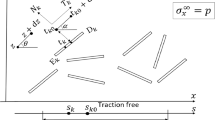
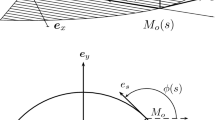
In this paper, a simple layer potential and a double layer potential are suggested to solve the curved crack problem. The complex potentials in the simple layer case are formulated on the distributed dislocation along the curve. Meantime, the complex potentials in the double layer case are formulated on the crack displacement opening distribution. Behaviors of the complex potentials, for example the behaviors of increments of some physical quantities around a large circle, are analyzed in detail. Continuity and discontinuity of some physical quantities in the normal direction of the curve are analyzed, which are key points for formulating the integral equations of the problems. One weaker singular, two singular and one hypersingular integral equations are suggested to solve the problems. The relations between the kernels in different integral equations are addressed. Similarly, a simple layer potential and a double layer potential are suggested to solve the curved rigid line problem. The complex potentials in the simple layer case are formulated on the distributed forces along the curve. Meantime, the complex potentials in the double layer case are formulated on the resultant force function. One weaker singular, two singular and one hypersingular integral equations are suggested to solve the problems. When the resultant forces and moment are applied on the deformable line, the constraint equations are suggested. For more general cases, for example, in the case that the tractions applied on the two crack faces are not same in magnitude and opposite in direction, a singular integral equation is suggested. The equation is obtained by a superposition of two kinds of single layer potentials.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • M. P Savruk (1981) Two-dimensional problems of elasticity for body with crack Naukova Dumka Kiev

    Google Scholar 

  • Y. K. Cheung Y. Z. Chen (1987) ArticleTitleNew integral equation for plane elasticity crack problem Theor. Appl. Fract. Mech. 7 177–184 Occurrence Handle88d:73055

    MathSciNet  Google Scholar 

  • C. K. Chao C. W. Young (1998) ArticleTitleOn the general treatment of multiple inclusions in antiplane elastostatics Int. J. Solids Struct. 35 3573–3593

    Google Scholar 

  • C. K. Chao J. Y. Lee (1996) ArticleTitleInteraction between a crack and a circular elastic inclusion under remote heat flow Int. J. Solids Struct. 33 3865–3880

    Google Scholar 

  • C. K. Chao M. H. Shen (1995) ArticleTitleSolutions of thermoelastic crack problems in bonded dissimilar media of half-plane medium Int. J. Solids Struct. 32 3537–3554

    Google Scholar 

  • W. L. Zang P. Gudmundson (1991) ArticleTitleKinked cracks in anisotropic plane modeled by an integral equation method Int. J. Solids Struct. 27 1855–1865

    Google Scholar 

  • W. L. Zang P. Gudmundson (1992) ArticleTitleKinked cracks in bonded half-planes modeled by an integral equation Int. J. Fract. 54 65–77

    Google Scholar 

  • N. I. Ioakimidis P. S. Theocaris (1979) ArticleTitleA system of curvilinear cracks in an isotropic elastic half-plane Int. J. Fract. 15 299–309 Occurrence Handle80e:73063

    MathSciNet  Google Scholar 

  • Y. Z. Chen D. Gross Y. J. Huang (1991) ArticleTitleNumerical solution of the curved crack problem by means of polynomial approximation of the dislocation distribution Eng. Fract. Mech. 39 791–797

    Google Scholar 

  • A. M Linkov (2002) Boundary integral equations in elasticity theory Kluwer Dordrecht

    Google Scholar 

  • Y. Z. Chen (2004) ArticleTitleSingular integral equation method for the solution of multiple curved crack problems Int. J. Solids Struct. 42 3505–3519

    Google Scholar 

  • B. Cotterell J. R. Rice (1980) ArticleTitleSlightly curved or kinked cracks Int. J. Fract. 16 155–169 Occurrence Handle10.1007/BF00012619

    Article  Google Scholar 

  • L. Dreilich D. Gross (1985) ArticleTitleThe curved crack Z. Angew. Math. Mech. (ZAMM) 65 132–134

    Google Scholar 

  • P. A. Martin (2000) ArticleTitlePerturbed cracks in two dimensions an integral-equation approach Int. J. Fract. 104 317–327 Occurrence Handle10.1023/A:1007610308529

    Article  Google Scholar 

  • Y. L. Xu (1995) ArticleTitleA concentric arc crack in a circular disc Int. J. Solids Struct. 32 2023–2040 Occurrence Handle0867.73067

    MATH  Google Scholar 

  • B. A. Cheeseman M. H. Santare (2000) ArticleTitleThe interaction of a curved crack with a circular elastic inclusion Int. J. Fract. 103 259–277 Occurrence Handle10.1023/A:1007663913279

    Article  Google Scholar 

  • Y. B. Wang K. T. Chau (2000) ArticleTitleA new boundary element for plane elastic problems involving cracks and holes Int. J. Fract. 87 1–20

    Google Scholar 

  • N. A. Noda T. Matsuo (1997) ArticleTitleNumerical solution of singular integral equations in stress concentration problems Int. J. Solids Struct. 34 2429–2444 Occurrence Handle1455737

    MathSciNet  Google Scholar 

  • X. D. Wang S. A. Meguid P. Papanikos (1999) ArticleTitleAnalysis of curved cracks emanating from adjacent holes Eng. Fract. Mech. 64 337–355

    Google Scholar 

  • Y. Z. Chen (1995) ArticleTitleA survey of new integral equation in plane elasticity crack problem Eng. Fract. Mech. 51 97–134

    Google Scholar 

  • Y. Z. Chen (1998) ArticleTitleComplex potentials in plane elasticity by distribution of dislocation or force doublet along a curve Int. J. Eng. Sci. 36 23–31

    Google Scholar 

  • Y. Z. Chen (1999) ArticleTitleStress intensity factors for curved and kinked cracks in plane extension Theor. Appl. Fract. Mech. 31 223–232

    Google Scholar 

  • Y. Z. Chen (1993) ArticleTitleNumerical solution of a curved crack problem by using hypersingular integral equation Eng. Fract. Mech. 46 275–283

    Google Scholar 

  • A. M. Linkov S. G. Mogilevskaya (1990) ArticleTitleHypersingular integrals in plane problems of the theory of elasticity Appl. Math. Mech. 54 93–99 Occurrence Handle91e:73025

    MathSciNet  Google Scholar 

  • A. M. Linkov S. G. Mogilevskaya (1994) ArticleTitleComplex hypersingular integrals and integral equations in plane elasticity Acta Mech. 105 189–205 Occurrence Handle10.1007/BF01183951 Occurrence Handle95c:73096

    Article  MathSciNet  Google Scholar 

  • S. G. Mogilevskaya (2000) ArticleTitleComplex hypersingular integral equation for the piece-wise homogeneous half-plane with cracks Int. J. Fract. 102 177–204 Occurrence Handle10.1023/A:1007633814813

    Article  Google Scholar 

  • Y. Z. Chen (2003) ArticleTitleA numerical solution technique of hypersingular integral equation for curve cracks Com. Numer. Meth. Eng. 19 645–655 Occurrence Handle01972236

    MATH  Google Scholar 

  • S. G. Moglivskaya L. Rothenburg M. B. Dusseault (2000) ArticleTitleInteraction between a circular opening and fractures originating from its boundary in a piecewise plane Int. J. Numer. Anal. Meth. Geomech. 24 947–970

    Google Scholar 

  • K. Mayrhofer F. D. Fischer (1992) ArticleTitleDerivation of new analytical solution for a general two-dimensional finite-part integral applicable in fracture mechanics Int. J. Numer. Meth. Engng. 33 1027–1047 Occurrence Handle10.1002/nme.1620330509 Occurrence Handle92m:73101

    Article  MathSciNet  Google Scholar 

  • J Hadamard (1923) Lectures on Cauchy’s problem in linear differential equations Yale University Press Yale

    Google Scholar 

  • P. A Martin F. J Rizzo (1989) ArticleTitleOn boundary integral equations for crack problems Proc. R. Soc. Lond. A421 341–355 Occurrence Handle90e:73104

    MathSciNet  Google Scholar 

  • S. Mukherjee (2000) ArticleTitleCPV and HFP integrals and their applications in the boundary element method Inter. J. Solids Struct. 37 6627–6634

    Google Scholar 

  • N. D. Aparicio (2000) ArticleTitleElastic complex analysis and its applications in fracture mechanics Int. J. Solids Struct. 37 3873–3895 Occurrence Handle01488671 Occurrence Handle2001d:74007

    MATH  MathSciNet  Google Scholar 

  • J. Helsing G. Peters (1999) ArticleTitleIntegral equation methods and numerical solutions of crack and inclusion problems in planar elastostatics SIAM J. Appl. Math. 59 965–982 Occurrence Handle10.1137/S0036139998332938 Occurrence Handle99j:73114

    Article  MathSciNet  Google Scholar 

  • Y. Z. Chen Z. W. Zhoa (1990) ArticleTitleNumerical solution of curve rigid line problem in an infinite plate Ing. Arch. 60 283–292

    Google Scholar 

  • Y. Z. Chen N. Hasebe (1992) ArticleTitleIntegral equation approaches for curved rigid line problem in an infinite plate Int. J. Fract. 58 1–20

    Google Scholar 

  • N. I Muskhelishvili (1953) Some basic problems of the mathematical theory of elasticity Noordhoff Amsterdam

    Google Scholar 

  • Y. Z Chen N Hasebe K. Y Lee (2003) Multiple crack problems in elasticity Southampton WIT Press

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Division of Engineering Mechanics, Jiangsu University, Zhenjiang, Jiangsu, 212013, P. R. China

    Y. Z. Chen & X. Y. Lin

Authors
  1. Y. Z. Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. X. Y. Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Y. Z. Chen.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chen, Y.Z., Lin, X.Y. Complex potentials and integral equations for curved crack and curved rigid line problems in plane elasticity. Acta Mechanica 182, 211–229 (2006). https://doi.org/10.1007/s00707-005-0305-4

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-005-0305-4

Keywords

Search

Navigation