Summary
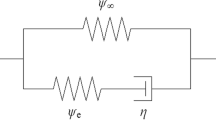
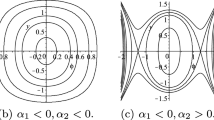
Stability studies of a tensegrity structure, used as a model for cell deformability, are performed. This structure is composed by six slender struts interconnected by 24 linearly elastic tendons and is prestressed. The tendons and the struts are governed by linear constitutive laws. The struts are allowed to buckle. Since the deformations are large, mathematical bifurcation theory working mainly for small deformations does not work. A general procedure for studying the stability behavior of the particular tensegrity model based upon the elastica theory is presented. The reference placement is defined by the prestress and the equilibrium placements are defined for any applied three-dimensional forces.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
R. B. Fuller (1961) ArticleTitleTensegrity Portfolio Artnews Annual 4 112–127 Occurrence Handle32 #9074
A. Pugh (1976) An introduction to tensegrity University of California Press Berkeley
Williams W. O.: A primer on the mechanics of tensegrity structures, notes, 2003.
R. Motro (1992) ArticleTitleTensegrity systems: the state of art Int. J. Space Struct. 7 IssueID2 75–83
Sultan C., Corless M., Skelton R. E.: The prestressability problem of tensegrity structures. Some analytical solutions. Int. J. Solids Struct. 38–39, 5223–5252 (2001).
D. E. Ingber (1993) ArticleTitleCellular tensegrity: defining new rules of biological design that govern the cytoskeleton J. Cell. Sci. 104 613–627
M. F. Coughlin D Stamenovic (1997) ArticleTitleA tensegrity structure with buckling compression elements: application to cell mechanics ASME J. Appl. Mech. 64 480–486
M. F. Coughlin D. Stamenovic (1998) ArticleTitleA tensegrity model of the cytoskeleton in spread and round cells J. Biomed. Engng. 120 770–777
D. Stamenovic M. F. Coughlin (1999) ArticleTitleThe role of prestresss and architecture of the cytoskeleton and deformability of cytoskeletal filaments in mechanics of adherent cells a quantitative analysis J. Theo. Biol. 201 63–74 Occurrence Handle10.1006/jtbi.1999.1014
D. Stamenovic M. F. Coughlin (2000) ArticleTitleA quantitative model of cellular elasticity based on tensegrity J. Biomech. Engng. 122 39–43
D. Stamenovic D. E. Ingber (2002) ArticleTitleModels of cytoskeletal mechanics of adherent cells Biomech. Model Mechanobiol. 1 95–108 Occurrence Handle10.1007/s10237-002-0009-9
K. Lazopoulos (2004) ArticleTitleStability of an elastic cytoskeletal tensegrity model Int. J. Solids Struct. 42 3459–3469
J. J. Stoker (1968) Nonlinear elasticity Gordon & Breach New York London
P. F. Byrd M. D. Friedman (1971) Handbook of elliptic integrals for engineers and scientists Springer Berlin
R. Ogden (1997) Nonlinear elastic deformations Dover New York
F. Gittes B. Mickey J. Nettleton J. Howard (1993) ArticleTitleFlexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape J. Cell Biol. 120 923–934 Occurrence Handle10.1083/jcb.120.4.923
H. Murakami Y. Nishimura (2003) Infinitesimal mechanism modes of tensegrity modules K. Watanabe F. Ziegler (Eds) Proc. IUTAM Symp. on Dynamics of Advanced Materials and Smart Structures Kluwer Academic Publishers Dordrecht 273–284
H. Murakami Y. Nishimura (2001) ArticleTitleStatic and dynamic characterization of some tensegrity modules J. Appl. Mech. 68 19–27 Occurrence Handle10.1115/1.1331058
H. Murakami Y. Nishimura (2001) ArticleTitleStatic and dynamic characterization of regular truncated icosahedral and dodecahedral tensegrity modules Int. J. Solids Struct. 38 9359–9381
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lazopoulos, K.A., Lazopoulou, N.K. On the elastica solution of a tensegrity structure: Application to cell mechanics. Acta Mechanica 182, 253–263 (2006). https://doi.org/10.1007/s00707-005-0288-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-005-0288-1