Summary
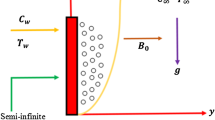
The effects of variable viscosity, thermophoresis and heat generation or absorption on hydromagnetic flow with heat and mass transfer over a heat surface are presented here, taking into account the homogeneous chemical reaction of first order. The fluid viscosity is assumed to vary as an inverse linear function of temperature. The velocity profiles are compared with previously published works and are found to be in good agreement. The governing fundamental equations are approximated by a system of nonlinear ordinary differential equations and are solved numerically by using the finite element method. The steady-state velocity, temperature and concentration profiles are shown graphically. It is observed that due to the presence of first-order chemical reaction the concentration decreases with increasing values of the chemical reaction parameter. The results also showed that the particle deposition rates were strongly influenced by thermophoresis and buoyancy force, particularly for opposing flow and hot surfaces. Numerical results for the skin-friction coefficient, wall heat transfer and particle deposition rate are obtained and reported graphically for various parametric conditions to show interesting aspects of the solution.
Similar content being viewed by others
References
Gebhart, B.: Heat transfer. New York: McGraw Hill, 1971.
Soundalgeker, V. M.: Free convection effects on Stokes problem for a vertical plate. J. Heat Transfer ASME 99C, 499–501 (1977).
Soundalgeker, V. M., Patil, M. R.: Stokes problem for vertical plate with constant heat flux. J. Astrophys Space Sci. 64,165–172 (1980).
Gebhart, B., Pera, L.: The nature of vertical natural convection flow resulting from the combined buoyancy effects of thermal and mass diffusion. J. Heat Mass Transfer 14, 2025–2050 (1971).
Fairbanks, D. F., Wike, C. R.: Diffusion and chemical reaction in an isothermal laminar flow along a soluble flat plate. Ind. Eng. Chem. Res. 42, 471–475 (1950).
Soundalgekar, V. M., Birajdar, N. S., Darwekar, V. K.: Mass transfer effects on the flow past an impulsively started infinite vertical plate with variable temperature or constant heat flux. Astrophys. Space Sci. 100, 159–164 (1984).
Muthucumaraswamy, R, Ganesan, P.: On impulsive motion of a vertical plate with heat flux and diffusion of chemically reactive species. Forsch. Ing.-Wes. 66, 17–23 (2000).
Ghaly, A. Y., Seddeek, M. A.: Chebyshev finite difference method for the effects of chemical reaction, heat and mass transfer on laminar flow along a semi infinite horizontal plate with temperature dependent viscosity. Chaos Solitons Fractals 19, 61–70 (2004).
Goren, S. L.: The role of thermophoresis in laminar flow of a viscous and incompressible fluid. J. Colloid Interface Sci. 61, 77 (1977).
Tsai, R.: A simple approach for evaluating the effect of wall suction and thermophoresis on aerosol particle deposition from a laminar flow over a flate plate. Int. Comm. Heat Mass Transf. 26, 249–257 (1999).
Chang, Y. P.,Tsai, R., Sui, F. M.: The effect of thermophoresis on particle deposition from a mixed convection flow onto a vertical flat plate. J. Aerosol Sci. 30,1363–1378 (1999).
Chamkha, A. J., Camille, I.: Effects of heat generation/absorption and thermophoresis on hydromagnetic flow with heat and mass transfer over a flat surface. Int. J. Num. Meth. Heat Fluid Flow 10, 432–448 (2000).
Chamkha, A. J., Pop, I.: Effect of thermophoresis particle deposition in free convection boundary layer from a vertical flat plate embedded in a porous medium. Int. Comm. Heat Mass Transf. 31, 421–430 (2004).
Herwing, H., Gersten, K.: The effect of variable properties on laminar boundary layer flow. Wärme Stoffübertr 20, 47–52 (1986).
Seddeek, M. A.: The effect of variable viscosity on hydromagnetic flow and heat transfer past a continuously porous boundary with radiation. Int. Comm. Heat Mass Transf. 27, 1037–1048 (2000).
Seddeek, M. A.: Effects of magnetic field and variable viscosity on forced non–Darcy flow about a flat plate with variable wall temperature in porous media in the presence of suction and bellowing. J. Appl. Mech. Tech. Phys. 43, 13–17 (2002).
Ling, J. X., Dybbs, A.: Forced convection over a flat plate submersed in a porous medium, variable viscosity case. Paper 87-WA/HT-23. New York: ASME 1987.
Weast, R. C.: Hand book of chemistry and physics, 67th ed. Boca Raton: C.R.C. Press 1986–1987.
Talbot, L., Cheng, R. K., Scheffer, R. W., Wills, D. P: Thermophoresis of particles in a heated boundary layer. J. Fluid Mech. 101, 737–758 (1980).
Shen, C.: Thermophoretic deposition of particles onto cold surface of bodies in two–dimensional and axi-symmetric flows. J. Colloid Interface Sci. 127, 104–115 (1989).
Batchelor, G. K., Shen, C.: Thermophoretic deposition in gas flow over cold surfaces. J. Colloid Interface Sci. 107, 21–37 (1985).
White, F.: Viscous fluid flow. 1st ed. New York: McGraw-Hill, 1974.
Reddy, J. N.: An introduction to the finite element method. McGraw-Hill International Editions 1984.
Bejan, A.: Convection heat transfer. 3rd ed. New York: Wiley 2004.
Bhargava, R., Kumar, L., Takhar, H. S.: Finite element solution of mixed convection micropolar flow driven by a porous stretching sheet. Int. J. Engng Sci. 41, 2161–2178 (2003).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Seddeek, M.A. Finite-element method for the effects of chemical reaction, variable viscosity, thermophoresis and heat generation/absorption on a boundary-layer hydromagnetic flow with heat and mass transfer over a heat surface. Acta Mechanica 177, 1–18 (2005). https://doi.org/10.1007/s00707-005-0249-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-005-0249-8