Abstract
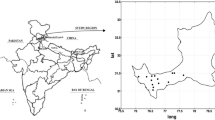
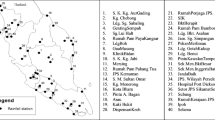
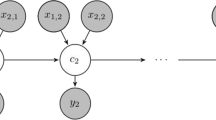
Non-homogeneous hidden Markov model (NHMM) is applied in modeling of daily rainfall occurrences across 16 synoptic stations in Kenya. The time series of the data sets was during the October–December (OND “short rains”) season from 1979 to 2005. The tool assumes that the diurnal rainfall events at a network of observing stations are influenced by unobserved states, that is, “weather states.” These states’ evolution is modeled based on a first-order Markov criterion with state-to-state transition probabilities conditioned on some atmospheric variable indices. The five states are selected using the Bayes information criterion (BIC). To downscale daily rainfall occurrences across 16 stations, a NHMM employed global circulation model (GCM) projection outputs for daily precipitation and sea surface temperatures during the study period. The interannual variability of the mean GCM simulated precipitation and mean historical stations rainfall depicts a weak correlation though significant at 90% confidence level. Thus, it implies that GCM-NHMM simulations do not simulate the rainfall occurrences well. The consecutive wet spell length between the historical rainfall datasets and GCM-NHMM simulated precipitation for 90-day frequencies shows a strong positive correlation significant at 95% confidence level. The findings from this study reveal that the modeling tool is suitable for statistical downscaling of daily rainfall occurrences at multisite stations network. The statistical inference from the model is applicable for drought/flood preparedness, water resource management, and inputs into crop models.















Similar content being viewed by others
References
Addinsoft (2016) XLSTAT, data analysis and statistics with MS excel. Addinsoft, NY, USA. https://www.xlstat.com/en/. Accessed 12 Apr 2018
Aerenson T, Tebaldi C, Sanderson B, Lamarque J-F (2018) Changes in a suite of indicators of extreme temperature and precipitation under 1.5 and 2 degrees warming. Environ Res Lett 13:035009. https://doi.org/10.1088/1748-9326/aaafd6
Bellone E, Hughes JP, Guttorp P (2000) A hidden Markov model for downscaling synoptic atmospheric patterns to precipitation amounts. Clim Res 15:1–12. https://doi.org/10.3354/cr015001
Cannon AJ, Whitfield PH (2002) Downscaling recent stream flow conditions in British Columbia, Canada using ensemble neural network models. J Hydrol 259:136–151. https://doi.org/10.1016/S0022-1694(01)00581-9
Charles S, Bates B, Smith I, Hughes P (2004) Statistical downscaling of daily precipitation from observed and modeled atmospheric fields. Hydrol Process 18:1373–1394. https://doi.org/10.1002/hyp.1418
Chen C, Baethgen WE, Robertson A (2013) Contributions of individual variation in temperature, solar radiation and precipitation to crop yield in the North China Plain, 1961–2003. Clim Chang 116:767–788. https://doi.org/10.1007/s10584-012-0509-2
Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer P, Bechtold P, Beljaars ACM, van de Berg L, Bidlot J, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Hólm EV, Isaksen L, Kållberg P, Köhler M, Matricardi M, McNally AP, Monge-Sanz BM, Morcrette J-J, Park B-K, Peubey C, de Rosnay P, Tavolato C, Thépaut J-N, Vitart F (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137:553–597. https://doi.org/10.1002/qj.828
Forney GD (1973) The Viterbi Algorithm. Proc IEEE 61:268–278
Funk C, Davenport F, Eilerts G, Nourey N, Galu G (2018) Contrasting Kenyan resilience to drought: 2011 and 2017. USAID Special Rep., 20 pp., www.usaid.gov/resilience/contrasting-kenyan-resilience-drought-2011-2017. Accessed 20 Aug 2019
Gabriel KR, Neumann J (1962) A Markov chain model for daily rainfall occurrences at Tel-Aviv. Q J R Meteorol Soc 88:85–90. https://doi.org/10.1002/qj.49708837511
Guo L, Jiang Z, Chen W (2018) Using a hidden Markov model to analyze the flood-season rainfall pattern and its temporal variation over East China. J Meteorol Res 32:410–420. https://doi.org/10.1007/s13351-018-7107-9
Huang, B., Banzon, V. F., Freeman, E., Lawrimore, J., Liu, W., Peterson, T. C.,... & Zhang, H. M. (2014). Extended reconstructed sea surface temperature version 4 (ERSST.v4): Part I. Upgrades and intercomparisons. J Clim 28:911–930. https://doi.org/10.1175/JCLI-D-14-00006.1
Hughes JP, Guttorp P (1994) A class of stochastic models for relating synoptic atmospheric patterns to regional hydrologic phenomena. Water Resour Res 30:1535–1546. https://doi.org/10.1029/93WR02983
Hughes JP, Guttorp P, Charles SP (1999) A non-homogeneous hidden Markov model for precipitation occurrence. J Royal Stat Soc: Series C (Appl Stat) 48:15–30. https://doi.org/10.1111/1467-9876.00136
IFRC Annual Report – 2014. (2015). https://media.ifrc.org/ifrc/wp-content/uploads/sites/5/2017/12/Annual-report-2014.pdf (Accessed 02 January 2018)
Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J, Zhu Y, Leetmaa A, Reynolds C, Chelliah M, Ebisuzaki W, Higgins W, Jonowiak J, Mo KC, Ropelewski C, Wang J, Wang J, Jenne R, Joseph D (1996) The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorol Soc 77:437–471. https://doi.org/10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2
Kang IS, Kim HM (2010) Assessment of MJO predictability for boreal winter with various statistical and dynamical models. J Clim 23:2368–2378. https://doi.org/10.1175/2010JCLI3288
Kass RE, Raftery AE (1995) Bayes factors. J Am Stat Assoc 90:773–795
Le Cam L (1961) A stochastic theory of precipitation. Fourth Berkeley Symposium on Mathematics, Statistics, and Probability. University of California, Berkeley, California 165–186. https://projecteuclid.org/euclid.bsmsp/1200512811
Maraun D, Wetterhall F, Ireson AM, Chandler RE, Kendon EJ, Widmann M, Brienen S, Rust HW, Sauter T, Themeßl M, Venema VKC, Chun KP, Goodess CM, Jones RG, Onof C, Vrac M, Thiele-Eich I (2010) Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev Geophys 48:RG3003. https://doi.org/10.1029/2009RG000314
McAvaney B, Covey C, Joussaume S, Kattsov V, Kitoh A, Ogana W, Pitman A, Weaver A, Wood R, Zhao Z-C (2001) Model evaluation. In: Houghton JT, Ding Y, Griggs DJ, Noguer M, van der Linden PJ, Dai X, Maskell K, Johnson CA (eds) Climate Change 2001:The Scientific Basis. Model Evaluation, Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA 881 pp
Mumo L, Yu J, Fang K (2018) Assessing impacts of seasonal climate variability on maize yield in Kenya. Int J Plant Prod 12:297–307. https://doi.org/10.1007/s42106-018-0027-x
Ongoma V, Chen H (2017) Temporal and spatial variability of temperature and precipitation over East Africa from 1951 to 2010. Meteorol Atmos Phys 129:131–144. https://doi.org/10.1007/s00703-016-0462-0
Ongoma V, Chen H, Gao C, Sagero PO (2017) Variability of temperature properties over Kenya based on observed and reanalyzed datasets. Theor Appl Climatol 133:1175–1190. https://doi.org/10.1007/s00704-017-2246-y
Ongoma V, Chen H, Gao C (2018) Projected change in mean rainfall and temperature over East Africa based on CMIP5 Models. Int J Climatol 38:1375–1392. https://doi.org/10.1002/joc.5252
Ongoma V, Chen H, Gao C (2019) Evaluation of CMIP5 twentieth century rainfall simulation over the equatorial East Africa. Theor Appl Climatol 135:893–910. https://doi.org/10.1007/s00704-018-2392-x
Pineda LE, Willems P (2016) Multisite downscaling of seasonal predictions to daily rainfall characteristics over Pacific–Andean River Basins in Ecuador and Peru Using a nonhomogeneous Hidden Markov model. J Hydrometeorol 17:481–498. https://doi.org/10.1175/JHM-D-15-0040.1
Robertson AW, Kirshner S, Smyth P (2004a) Downscaling of daily rainfall occurrence over Northeast Brazil using a Hidden Markov Model. J Clim 17:4407–4424. https://doi.org/10.1175/JCLI-3216.1
Robertson AW, Lall U, Zebiak SE, Goddard L (2004b) Improved combination of multiple atmospheric GCM ensembles for seasonal prediction. Mon Weather Rev 132:2732–2744. https://doi.org/10.1175/MWR2818.1
Robertson AW, Kirshner S, Smyth P, Charles SP, Bates BC (2005) Subseasonal-to-interdecadal variability of the Australian monsoon over North Queensland. QJR Meteorol Soc 132:511–542. https://doi.org/10.1256/qj.05.75
Robertson AW, Moron V, Swarinoto Y (2009) Seasonal predictability of daily rainfall statistics over Indramayu district, Indonesia. Int J Climatol 29:1449–1462. https://doi.org/10.1002/joc.1816
Rowell DP (2019) An Observational Constraint on CMIP5 Projections of the East African Long Rains and Southern Indian Ocean Warming. Geophys Res Lett 46:6050–6058. https://doi.org/10.1029/2019GL082847
Schubert S (1998) Downscaling local extreme temperature changes in south-eastern Australia from the CSIRO Mark2 GCM. Int J Climatol 18:1419–1438. https://doi.org/10.1002/(SICI)1097-0088(19981115)18:13<1419::AID-JOC314>3.0.CO;2-Z
Steduto P, Hsiao TC, Raes D, Fereres E (2009) AquaCrop—The FAO crop model to simulate yield response to water: I. Concepts and underlying principles. Agron J 101:426–437. https://doi.org/10.2134/agronj2008.0139s
Stern RD, Coe R (1984) A model fitting analysis of daily rainfall data. J R Statist Soc A 147:1–34
Timbal B, Dufour A, McAvaney B (2003) An estimate of future climate change for western France using a statistical downscaling technique. Clim Dyn 20:807–823. https://doi.org/10.1007/s00382-002-0298-9
Verbist K, Robertson AW, Cornelis WM, Gabriels D (2010) Seasonal predictability of daily rainfall characteristics in central northern Chile for dry-land management. J Appl Meteorol Climatol 49:1938–1955. https://doi.org/10.1175/2010JAMC2372.1
Vrugt JA, Ter Braak CJ, Clark MP, Hyman JM, Robinson BA (2008) Treatment of input uncertainty in hydrologic modeling: doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour Res 44:W00B09. https://doi.org/10.1029/2007WR006720
Waymire E, Gupta VK (1981) The mathematical structure of rainfall representations 2. A review of the theory of point processes. Water Resour Res 17:1273–1285. https://doi.org/10.1029/WR017i005p01273
Wilby RL, Charles SP, Zorita E, Timbal B, Whetton P, Mearns LO (2004) Guidelines for use of climate scenarios developed from statistical downscaling methods. Supporting material of the Intergovernmental Panel on Climate Change. http://www.ipcc-data.org/guidelines/dgm_no2_v1_09_2004.pdf (Accessed on 05 June 2017)
Wood AW, Leung LR, Sridhar V, Lettenmaier DP (2004) Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim Chang 62:189–216. https://doi.org/10.1023/B:CLIM.0000013685.99609.9e
Yoo JH, Robertson AW, Kang IS (2010) Analysis of intraseasonal and interannual variability of the Asian summer monsoon using a hidden Markov model. J Clim 23:5498–5516. https://doi.org/10.1175/2010JCLI3473.1
Zeng G, Wang WC, Shen C, Hao Z (2014) Summer precipitation changes over the Yangtze River Valley and North China: simulations from CMIP3 models. Asia Pac J Atmos Sci 50:355–364. https://doi.org/10.1007/s13143-014-0022-9
Zucchini W, Guttorp P (1991) A hidden Markov model for space-time precipitation. Water Resour Res 27:1917–1923. https://doi.org/10.1029/91WR01403
Acknowledgments
The authors express their appreciation to Ms. Lianyi Guo’s thoughtful suggestions and all the data sources. Special thanks go to Nanjing University of Information Science and Technology (NUIST) for promoting a research enabling atmosphere that facilitated completion of this work. Special thanks to NCEP/NCAR and KMD for providing the data used in this study.
Funding
This study was supported by funds from the National Key Research and Development Program of China (Grant No. 2017YF0603804) and the National Natural Science Foundation of China (Grant No. 41575085 and No. 41430528).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Nyongesa, A.M., Zeng, G. & Ongoma, V. Non-homogeneous hidden Markov model for downscaling of short rains occurrence in Kenya. Theor Appl Climatol 139, 1333–1347 (2020). https://doi.org/10.1007/s00704-019-03016-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-019-03016-2