Abstract
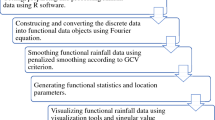
The main concern of this study is to build a functional data object from discrete rainfall observations by looking at how rainfall fluctuates, both spatially and temporally, in the form of smoothing curves. The functional data methods employed in this study are able to extract additional information contained in the function and its derivatives which may not be normally available from traditional statistical methods. Functional concepts such as functional descriptive statistics and functional analysis of variance were applied to describe the spatial and temporal rainfall variations at the stations and at any time throughout the year. This study involves 32 rainfall stations in Peninsular Malaysia and rainfall records for 32 years. Eleven basis functions were used to describe the unimodal rainfall pattern for stations in the East Peninsula, while five and seven bases were required to describe the rainfall pattern for stations in the northwest, west, southwest, and central regions of the peninsula. Based on the location and scale curves, the highest mean and the highest variability of rainfall were observed during the northeast monsoon flow. On the other hand, the concept of functional analysis of variance allows the detailed information in determining when, in a time series, differences may exist in rainfall profiles between two or more regions. In general, the findings suggested that the rainfall profiles of the regions are very dependent on their geographical and spatial locations, as well as the monsoon effect, which reflects the time of year.






Similar content being viewed by others
References
Burauskaite-Harju A, Grimvall A, Achberger C, Walther A, Chen D (2012) Characterising and visualizing spatio-temporal patterns in hourly precipitation records. Theor Appl Climatol 109:333–343. doi:10.1007/s00704-011-0574-x
Chebana F, Dabo-Niang S, Ouarda TBMJ (2012) Exploratory functional flood frequency analysis and outlier detection. Water Resour Res 48:W04514. doi:10.1029/2011WR011040
Craven P, Wahba G (1979) Smoothing noisy data with spline functions: estimating the correct degree of smoothing by the method of generalized cross-validation. Num Math 31:377–403
Cuesta-Albertos JA, Fraiman R (2007) Impartial trimmed k-means and classification rules for functional data. Comput Stat Data Anal 51:4864–4877
Cuevas A, Febrero M, Fraiman R (2004) An ANOVA test for functional data. Comput Stat Data Anal 47:111–122
Deni SM, Jemain AA, Ibrahim K (2008) The spatial distribution of wet and dry spells over Peninsular Malaysia Theor. Appl Climatol 94:163–173. doi:10.1007/s00704-007-0355-8
Deni SM, Jemain AA, Ibrahim K (2009) Fitting optimum order of Markov chain models for daily rainfall occurrences in Peninsular Malaysia. Theor Appl Climatol 97:109. doi:10.1007/s00704-008-0051-3
Desa MN, Niemczynowicz J (1996) Temporal and spatial characteristics of Kuala Lumpur in Malaysia. Atmos Res 42:263–267
Ellouze M, Azri C, Abida H (2009) Spatial variability of monthly and annual rainfall data over southern Tunisia. Atmos Res 93:832–839
Febrero M, Galeano P, Manteiga WG (2007) A functional analysis of NOx levels: location and scale estimation and outlier detection. Comput Stat 22:411–427
Ferraty F, Rabhi A, Vieu P (2005) Conditional quantiles for functional dependent data with application to the climatic El Niño phenomenon. Sankhya 67:378–398
Gao HO (2007) Day of week effects on diurnal ozone/NOx cycles and transportation emissions in Southern California. Transportation Research Part D12:292–305
Giuseppe ED, Lasinio GJ, Esposito S, Pasqui M (2013) Functional clustering for Italian climate zones identification. Theor Appl Climatol 114:39–54
Green PJ, Silverman BW (1994) Nonparametric regression and generalized linear models: a roughness penalty approach. Chapman and Hall, London
Grossman A, Morlet J (1984) Decomposition of Hardy functions into square integrable wavelets of constant shape. SIAM J Math Anal 15:723–736
Harezlak J, Coull B, Laird N, Magari S, Christiani D (2007) Penalized solutions to functional regression problems. Comput Stat Data Anal 51:4911–4925
Hlubinka D, Prchal L (2007) Changes in atmospheric radiation from the statistical point of view. Comput Stat Data Anal 51:4926–4941
Hyndman R, Ullah S (2007) Robust forecasting of mortality and fertility rates: a functional data approach. Comput Statist Data Anal 51:4942–4956
Ideião SAM (2005) Analysis of precipitation time series using the wavelet transform. Sociedade & Natureza, Uberlândia Special Issue, pp. 736–745
Ignaccolo R, Ghigo S, Giovenali E (2008) Analysis of air quality monitoring networks by functional clustering. Environmentrics 19:672–686
Kaziska DM (2014) Functional analysis of variance, discriminant analysis, and clustering in a manifold of elastic curves. Communications In Statistics-Theory And Methods 40(14):2487–2499
Kim BR, Zhang L, Berg A, Fan J, Wu R (2008) A computational approach to the functional clustering of periodic gene-expression profiles. Genetics 180:821–834
Labat D, Ababou R, Mangin A (2001) Introduction of wavelet analyses to rainfall/runoffs relationship for a Karstic Basin: the case of Licq-Athrey karstic system (France). Ground Water 39(4):605–615
Laukaitis A, Rackauskas A (2005) Functional data analysis for clients segmentation tasks. Eur J Oper Res 163:210–216
Lim JT (1976) Rainfall minimum in Peninsular Malaysia during the northeast monsoon. Mon Weather Rev 104:96–99
Mante C, Yao AF, Degiovanni C (2007) Principal component analysis of measures with special emphasis on grain-size curves. Comput Stat Data Anal 51:4969–4983
Nerini D, Ghattas B (2007) Classifying densities using functional regression trees: applications in oceanology. Comput Statist Data Anal 51:4984–4993
Ramsay JO, Silverman B (2005) Functional data analysis, Springer Series in Statistics. Springer, New York
Ramsay JO, Hooker G, Graves S (2009) Functional data analysis with R and MATLAB. Springer, New York
Salarpour M, Yusop Z, Yusof F (2012) Modeling the distributions of flood characteristics for a tropical river basin. J Environ Sci Technol 5(6):419–429. doi:10.3923/jest.2012.419.429
Santos CAG, Galvao CO, Suzuki K, Trigo RM (2001) Matsuyama city rainfall data analysis using wavelet transform. Ann J Hydraul Engng, JSCE 45:211–216
Suhaila J, Jemain AA (2012) Spatial analysis of daily rainfall intensity and concentration index in Peninsular Malaysia. Theor Appl Climatol 108:235–245. doi:10.1007/s00704-011-0529-2
Suhaila J, Deni SM, Wan Zin WZ, Jemain AA (2010) Spatial patterns and trends of daily rainfall regime in Peninsular Malaysia during the southwest and northeast monsoons: 1975-2004. Meteorog Atmos Phys 110:1–18. doi:10.1007/s00703-010-0108-6
Suhaila J, Jemain AA, Hamdan MF, Wan Zin WZ (2011) Comparing rainfall patterns between regions in Peninsular Malaysia via functional data analysis technique. J Hydrol 411:197–206
Svensson C (1999) Empirical orthogonal function analysis of daily rainfall in the upper reaches of the Huai River Basin, China. Theor Appl Climatol 62:147–161
Tokushige S, Yadohisa H, Inada K (2007) Crisp and fuzzy k-means clustering algorithms for multivariate functional data. Comput Stat 22:1–16
Acknowledgments
We would like to extend our sincere gratitude to the Ministry of Education Malaysia for the financial support given for this work under the post-doctoral scheme and through research grant FRGS 4F686. We would also like to acknowledge Universiti Teknologi Malaysia and JSPS Asian Core Program for their support in conducting workshops and activities. Finally, special thanks to Professor Dr. Abdul Aziz Jemain from Universiti Kebangsaan Malaysia for his advice and comments throughout the research.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Suhaila, J., Yusop, Z. Spatial and temporal variabilities of rainfall data using functional data analysis. Theor Appl Climatol 129, 229–242 (2017). https://doi.org/10.1007/s00704-016-1778-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-016-1778-x