1 Introduction

An understanding of temporal and spatial characteristics of rainfall is central to water resources planning and management especially with evidence of climate change and variability in recent years. Such information is important in agricultural planning, flood frequency analysis, flood hazard mapping, hydrological modelling, water resource assessments, climate change impacts and other environmental assessments (Michaelides et al. 2009). Many studies on the temporal and spatial characteristics of rainfall in different parts of the world were therefore carried out (e.g. Zhang et al. 2008, 2009a, b, c, 2010; Turks 1996; De Luís et al. 2000; Gonzalez-Hildago et al. 2001; Cannarozzo et al. 2006; Chu et al. 2010). Different changing properties have been detected depending on the climatic regions, seasons, precipitation parameters (mean, maximum, minimum), etc. These studies suggest that rigorous studies have to be carried out at global, national and local scales using different methodologies. No individual method can reveal the different statistical properties of precipitation variability, and each method has its own strength and weakness. The results of different methods can complement each other.

Previous studies have also highlighted the knowledge gap in the understanding of rainfall characteristics, especially in many developing countries (Desa and Niemicynowicz 1996). The absence of high-quality climatic data at the desired spatial and temporal scales, lack of research attention, capacity and political will, as well as political turmoil in certain cases, have all been cited amongst the factors contributing to the knowledge gap in the Southern and Eastern Africa region (Sene and Farquharson 1998; Alemaw and Chaoka 2002; Shongwe et al. 2006; Sawunyama and Hughes 2008; Kizza et al. 2009). Despite data limitations, studies in Southern Africa have nevertheless revealed a more heterogeneous spatial and temporal regional rainfall pattern than in many other regions of the world (e.g. New et al. 2006; Mason et al. 1999; Nel 2009; Morishima and Akasaka 2010; Kampata et al. 2008; Batisani and Yarnal 2010; Love et al. 2010; Kizza et al. 2009). Shongwe et al. (2009) observed changes in the mean rainfall varying on relatively small spatial scales and differing between seasons, which cannot be fully revealed in regional-based studies as mentioned above. This finding partly motivated our study to further investigate such temporal and spatial rainfall characteristics for Malawi at a much finer spatial scale using all updated data available.

Malawi is an agro-based economy where 90% of the agriculture is predominantly rain-fed. Improving the understanding of temporal and spatial structures of rainfall is therefore key to the country’s economic development. Studies on Malawi’s rainfall characteristics are very scarce in the literature. Documented cases include those by Jury and Mwafulirwa (2002) and Jury and Gwazantini (2002) who respectively developed rainfall and flood forecasting predictive models over tropical southern Africa based on climate variability (1961–1995) and Lake Malawi levels (1937–1995). During the International Decade of the East African Lakes (IDEAL) from 1990 to 2000, past temporal and spatial climate variabilities were unveiled from Lake Malawi sediment and isotope records (e.g. Johnson et al. 2001). The IDEAL studies mostly involved temporal scales extending back to hundreds and thousands of years ago. More recently, the Lake Malawi drilling project took a similar approach (Lyons et al. 2011). Some single station-based analyses include those Ngongondo (2006) and Mbano et al. (2008) which examined rainfall trends at two stations in Southern Malawi. Other studies have mostly been along the lines of adaptation to climate change and variability (e.g. Tadross et al. 2007).

This study is an initial part of ongoing research on the hydrological modelling of water resources under present and changing climate conditions in Malawi. It departs from most previous studies involving Malawi which mainly looked at larger spatial dimensions of Africa or the Southern Africa region. The main objective of the study was to improve our understanding of the rainfall regime in Malawi which was achieved through: (a) Examining the spatial correlations of month-to-month (monthly hereafter), seasonal (wet and dry), annual and individual month’s rainfall amounts over Malawi and their pattern of variations in the year and (b) investigating and quantifying the temporal trends and their spatial variations.

The spatial and temporal characteristics of the rainfall should unveil whether the underlying generation processes of the rainfall at the various stations are spatially independent or dependent. This would be useful in decision making for choosing the appropriate aggregation approaches for subsequent hydrological modelling studies. Furthermore, the study will provide a database for ongoing and future studies as well as for those responsible for water resources management and agriculture in the country and the region.

2 Study area and database

Malawi is a landlocked country lying between 9° S and 17° S and longitudes 32–36° E in Southern Africa. The whole country is part of the Zambezi River basin, contributing to about 8% of the Zambezi basin’s total catchment area. Lake Malawi (Fig. 1) is a dominant water resources feature of the country, covering about one fifth of the country’s area of 118,000km2 and two thirds of the country’s length. The lake is in the East African Rift Valley at about 474 m above sea level, with a surface area of 2.8 × 104 km2, a volume of 8 × 103 km3, a land catchment area of 9.6 × 104 km2, a length of 550 km and a breadth of 15–80 km; it forms borders between Malawi, Mozambique and Tanzania. Six small rivers create an annual inflow of approximately 360 m3 s−1 to the lake. The Shire River drains the lake southward over a weir to the Zambezi River (Jury and Gwazantini 2002; Jury and Mwafulirwa 2002).

Fig. 1
figure 1

Map of Malawi with graphs of monthly mean rainfall distribution at selected study stations in Malawi

Full size image

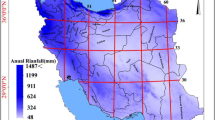
Malawi’s climate is tropical wet and dry, also known as savanna. It is mostly dominated by the north–south migration of the intertropical convergence zone (ITCZ). The ITCZ is marked by the convergence of northeasterly monsoon and southeasterly trade winds. The ITCZ works in collaboration with the Congo air boundary, the northwest winter monsoons comprising recurving tropical Atlantic Air that reaches Malawi through the Congo Basin. The main rain season is from November to April and the dry season is from May to October. Tropical cyclones originating from the Indian Ocean are frequent during the main rain season, and these bring in very intense rainfall activities over a few days. Annual rainfall in Malawi varies from 700 mm in the low-lying areas to 2,500 mm in the southern and parts of the northern highlands. Some areas, especially the highlands to the south of the country, experience sporadic winter rains locally called chiperone between May and August. These rains originate from an influx of cool moist southeast winds during the period. Figure 1 shows the typical annual rainfall distribution at selected rainfall stations in Malawi.

2.1 Database formulation

2.1.1 Data sources

Monthly rainfall data for the period between 1960 and 2001 at 42 spatially representative stations in Malawi were obtained from the Malawi Meteorological Services Department. These data underwent some quality control procedures recommended by the World Meteorological Organization (WMO) at the Southern Africa Drought Monitoring Centre in Harare, Zimbabwe (Shongwe et al. 2009).

In addition, daily data from 1978 to 2008 for ten stations in Southern Malawi were also obtained from the Malawi Department of Climate Change and Meteorological Services. The monthly data for some stations in Southern Malawi were extended to 2008 using monthly totals derived from the daily data where possible. The monthly data derived from the daily data also provided a comparison platform with the monthly totals for the overlapping periods. Additional daily data were obtained from the University of Malawi, Chancellor College Weather Station for the period 1974–2007, Illovo Sugar Company at Nchalo Sugar Estate station for 1971–2008 and Alumenda Sugar Estate station for 1998–2008. Table 1 gives some descriptive statistics of the rainfall stations used, including their location, elevation and period of record. The data were analysed at annual, seasonal (wet and dry), monthly and individual month’s timescales.

Table 1 Summary information of the rainfall stations used in the study
Full size table

2.1.2 Database construction

The daily and monthly data required careful scrutiny which necessitated the construction of a database. We observed that some missing entries were just reported as zeros, and blanks were frequent. For the treatment of records with missing gaps, Vicente-Serrano et al. (2010) observed that there are no general criteria in the literature for the selection of observatories suitable for reconstruction. Shongwe et al. (2006) suggested the use of data from stations with not more than 5% missing records, which can be a major challenge to achieve especially in data-scarce regions. We therefore adopted the more flexible 10% maximum threshold recommended by Hosking and Wallis (1997) considering that data availability in the study area is a challenge. The data series were arranged to follow Malawi’s hydrological year from November to October.

3 Methodology

The study approach is summarised as follows and details are presented in the subsections in this chapter: Database construction and quality control of the rainfall data were first performed by checking for outliers and temporal homogeneity, investigation of the spatial distribution patterns of the various rainfall variables throughout Malawi was carried out, and analysis of various rainfall variables was done to understand the temporal characteristics of rainfall in Malawi.

3.1 Outlier detection, quality control and homogenisation

The broader data quality control and homogenisation scheme used in this study has been applied by many investigators, including Vicente-Serrano et al. (2010) and Štěpánek et al. (2009). The first step involves outlier detection. his can be achieved either by spatial analysis techniques comparing the candidate station to neighbouring stations using some scheme. Among factors that can assist with the selection of reference stations, distance from the tested site, correlation, elevation, landscape features, vegetation, length of record and amount of missing data were considered (Vincent 1998).

Outliers were screened using the Tukey fence. This approach is recommended for non-normally distributed data like rainfall. The Tukey fence is the data range \( \left[ {{Q_1} - 1.5 \times {\rm IQR}, \;{Q_3} + 1.5 \times {\rm IQR} } \right] \), where Q 1 and Q 3 are respectively the lower and upper quartile points (25% of the data are less or more than those points, respectively), 1.5 are standard deviations from the mean, and IQR is the interquartile range. Values outside the Tukey fence are considered as outliers. In this study, such outliers were set to a limit value corresponding to 1.5 × IQR.

Methods for data homogenisation, their respective advantages and weakness have been discussed extensively in the literature. Examples of the methods include: Kohler’s double mass analysis; cumulative deviations; the standard normal homogenisation test (SNHT), also called the Alexandersson test; cumulative deviations method; Worsely’s likelihood ratio test; the residual test by the WMO; the bivariate test, the penalised maximal t test; and the regression-based Eastering and Petterson test, which was modified to the multiple regression-based Vincent test. A comprehensive review of the methods is presented by Peterson et al. (1998). Easterling and Peterson (1992) recommended that the SNHT (also called the Alexandersson test) by Alexandersson (1986) was the most effective method for homogeneity testing.

In this study, we used the cumulative deviations test for absolute testing (i.e. using stations own records) by Buishand (1982) owing to its lower demands in application and interpretation. We further applied the recommended SNHT by Alexandersson (1986) for relative testing using neighbouring stations. The data quality control and homogenisation were achieved using the free version of the software Anclim by Stepánek (2007).

3.2 Test of randomness and persistence

The data analysis procedures for trend detection used require that the data should be random and persistence-free, that is, not influenced by rainfall in the previous time step. The autocorrelation function was used to test for such randomness and independence (von Storch 1995):

$$ {r_k} = \frac{{\sum\limits_{{i = 1}}^{{N - k}} {({x_i} - m)({x_{{i + k}}} - m)} }}{{\sum\limits_{{i = 1}}^N {{{({x_i} - m)}^2}} }} $$
(1)

where r k is the lag-k autocorrelation coefficient, m is the mean value of a time series x i , N is the number of observations, and k is the time lag.

Random series have autocorrelations near zero for all time lag separations, except the zero lag coefficient which is always 1. In that case, statistical tests are directly applied to the series. Non-random series have one or more significantly non-zero autocorrelation values, and statistical tests in this case are applied to a pre-whitened series to account for the non-randomness.

3.3 Spatial characteristics

The spatial structure of rainfall between the various stations was examined using the spatial correlation function (SCF; Sen and Habib 2001):

$$ {R_{{i,j}}} = \frac{{\overline {\left( {Z_i^0 - \overline {{Z_i}} } \right)\left( {Z_j^0 - \overline {{Z_j}} } \right)} }}{{\overline {\left( {Z_i^0 - \overline {{Z_i}} } \right)\left( {Z_j^0 - \overline {{Z_j}} } \right)} }} $$
(2)

where R ij is the empirical SCF between two stations i and j with rainfall observations \( Z_i^0 \) and \( Z_j^0 \) and mean rainfall \( \overline {{Z_i}} \) and \( \overline {{Z_j}} \), respectively, for any distance D ij between the two stations. The overbars indicate time averages over a long sequence of past observations. The stations in this study therefore had a total of n(n − 1)/2 pairs of correlation coefficients and corresponding distances. A scatter plot of the R ij against D ij may reveal the underlying spatial correlation structure with distance amongst the stations. The assumption is that two data sets for stations that are closer to each other should exhibit stronger correlation. Further assumption is that the correlation function is homogenous and isotropic in the area, hence is a function of distance only. Depending on the nature of the underlying generation process, the correlation may decrease or not with distance. Some studies have suggested that the correlation decrease with distance in many cases follows the negative exponential model of the form:

$$ {R_{{ij}}} = a \times \exp \left( { - b \times {D_{{ij}}}} \right) $$
(3)

where a and b are the model parameters which can be found by the classical least squares technique. The station correlation assumes values in the range depending on the level of correlation amongst stations. Maximum inter-station distance was 760 km, and this was between stations located to the north and south of Malawi.

Spatial patterns of the correlations and trends across the country were investigated using ordinary kriging interpolation method (Singh and Chowdhury 1986; Lebel et al. 1987; De Luís et al. 2000, Miras-Avalos et al. 2007, Yang et al. 2010). This method was chosen as it is more robust in spatial interpolation in sparsely sampled regions and the study area is such an ideal case (Yang et al. 2010). To visualise the spatial correlation patterns R ij , the correlations of the observation station at Kamuzu International Airport in Central Malawi with the rest of the stations were interpolated on a map of Malawi. The GEOR package of the free statistical software R was used for the simple kriging spatial interpolation (R Development Core Team 2008).

3.4 Temporal trend analysis

The WMO recommends the non-parametric Mann–Kendall (MK) test statistic (Mann 1945; Kendall 1975) for the assessment of trends in meteorological data (WMO 1988). The test has been widely applied in various trend detection studies including those of Kampata et al. (2008) in the Zambian part of the headwaters of the Zambezi River basin in Southern Africa, Burn and Hag Elnur (2002) in Canada, Chen et al. (2009) in China, Kizza et al. (2009) in the Lake Victoria Basin and Chowdhury and Beechman (2010) in Australia. The MK test is considered more robust over many parametric tests as it is insensitive to missing data and outliers. The test is also recommended for non-normally distributed data series such as rainfall (Lettenmaier et al. 1994). We therefore applied the MK test at a significance level of 5% to study the temporal trends of the following: total annual rainfall (R) and its coefficient of variability (CVR), wet and dry season total rainfall (i.e. November to April and May to October, respectively), and month-to-month and monthly total rainfall series. At monthly scale, each month was treated as an individual season in a year; hence, each station had 12 such monthly series forming annual series. The slope of the trends was quantified by a linear regression model of the form:

$$ y = mx + c $$
(4)

where y is the rainfall amount (mm), x is the number of years of the series (end year − start year), m is the slope of the trend (mm/year) indicating the detected change, and c is a regression coefficient.

In addition, monthly rainfall heterogeneity was investigated using the precipitation concentration index series and its coefficient of variability originally by Oliver (1980) and modified by De Luís et al. (2000):

$$ {\rm PCI} = 100 \times \left[ {\sum {p_i^2} /{{\left( {\sum {{p_i}} } \right)}^2}} \right] $$
(5)

where p i is the monthly rainfall (mm). Annual PCIs were calculated for each of the stations record length. PCI values <10 indicate uniform monthly rainfall distribution, whilst those between 11 and 20 suggest high monthly concentration and those over 20 indicate very high monthly concentration.

Furthermore, the normalized precipitation anomaly series of R(AR) and PCI (APCI) were used to test for inter-annual rainfall variability (De Luís et al. 2000). For a given station s and for a given year y, the ratio of each value to the mean for the reference period is defined as:

$$ A{R_{{sy}}} = \left( {{R_{{sy}}} - {R_{{\rm s} }}} \right)/{R_{{\rm s} }};A{{\rm PCI}_{{{\rm sy} }}} = \left( {PC{I_{{sy}}} - \overline {PC{I_s}} } \right)/\overline {{{{\rm PCI} }_s}} . $$
(6)

The absolute values of the anomaly series (|AR| and |APCI|) were used to detect changes in the amplitude of the inter-annual variability of the series.

4 Results and discussions

4.1 Quality control and homogeneity

Two stations, Nkhatabay and Dedza, had suspected outliers. These were adjusted using the Tukey fence and compared with their closest neighbours on the Euclidian distance, Mzuzu and Dowa, as references for similar temporal behaviour, respectively.

The cumulative deviations test statistics for all stations were below the critical values at the 5% significance level. The results therefore suggest that most of the stations were absolutely homogeneous. Applying the SNHT, most stations also exhibited relative homogeneity as all test statistics were less than the critical values for the test. Nkhatabay and Dedza stations again showed some inhomogeneity, and the data values were adjusted using a reference series created by three nearby stations.

4.2 Spatial and temporal characteristics

4.2.1 Serial correlation

In the examination of the autocorrelation functions for each of the individual months, seasonal (wet and dry) and annual rainfall time series for each station did not reveal any significant serial correlation at all lags. These series were therefore random, hence meeting the independently identical distribution criteria. In these cases, the Mann–Kendall test can be applied directly to the series.

However, autocorrelation functions of the month-to-month series had strong 12-month cyclicity, as shown by the lag-24 superimposed autocorrelation plots of all stations in Fig. 2.

Fig. 2
figure 2

Autocorrelation functions for the 42 stations in Malawi used in this study

Full size image

From Fig. 2, a clearly sinusoidal autocorrelation pattern is evident for all the stations. This cyclicity is due to the strong seasonality of the climate. The month-to-month series are therefore not independent. In this case, the Mann–Kendall test statistics cannot be applied directly to the series as trends in seasons with small values can be dominated by seasons with larger values. To overcome this limitation, analysing the trends at annual, seasonal and individual month’s rainfall series should partially simplify the complexity introduced by serial correlation in the month-to-month series (Lettenmaier et al. 1994). Furthermore, the effect of seasonality in the month-to-month series was removed by applying the seasonal Mann–Kendall statistic (SMK) (Hirsch et al. 1982; Lettenmaier et al. 1994) given as:

$$ {S_{{\rm s} }} = \sum\nolimits_{{k = 1}}^{{{n_{{\rm s} }}}} {{S_k}} $$
(7)

where S s is the trend for each of the individual month’s annual series in a hydrological year in Malawi from November to October. The SMK test is advantageous as it accounts for serial dependence by incorporating a covariance term into the calculation of variance of Mann–Kendall statistics (Hirsch and Slack 1984).

4.2.2 Spatial correlation

Spatial rainfall correlation in Malawi was varied at all scales. For illustrative purposes, the SCFs for the annual, seasonal (total rainfall from November to April), March (highest spatial correlation) and August (lowest spatial correlation) are shown in Fig. 3. The cross-correlations showed that with average inter-station distance of 245 km, the monthly series had the highest average inter-station correlation of +0.72. March had the highest average inter-station correlation of +0.40 for the individual month’s series, and this was lowest in August at +0.17. The average inter-station spatial correlations for the annual and seasonal rainfall were both around +0.37, in line with the seasonal nature of the rainfall. The decline of the spatial correlations with distance is evident in Fig. 3, although the large scatter of the points is masking the pattern.

Fig. 3
figure 3

Empirical spatial correlations for annual, seasonal, March and August from top to bottom, respectively

Full size image

The scatter in Fig. 3 is normally random and should be expected in cases where observation stations are not evenly distributed throughout an area, as was in this study. The effect of the scatter can be removed by averaging out the correlations at various subjective distance intervals (Thiebaux and Pedder 1987; Sen and Habib 2001). An averaging distance interval of 20 km was therefore chosen as it reasonably demonstrated the spatial correlation pattern. For illustration, Fig. 4 shows the annual, monthly, March and August spatial correlations at 20-km averaging distances.

Fig. 4
figure 4

Spatial correlations for annual, monthly, March and August rainfall series averaged at 20-km intervals

Full size image

From Fig. 4, all series show that spatial correlation amongst the stations is highest (mostly above +0.85) in the first 20 km, only after which various degrees of decline are exhibited. The monthly series showed the highest spatial correlation even at large separation distances. These series had maximum average spatial correlation of +0.96 in the first 20 km and a minimum of +0.79 in the first 100 km. For the individual month’s series, the spatial correlations all decayed with distance after the first 20 km. At distances >20 km, the highest spatial correlations were in March during the rain season, whereas August during the dry season had the lowest spatial correlations. Other rain season months from November to April, not included in Fig. 4, also exhibited relatively higher spatial correlations as compared to dry season months between May and October. This seasonal difference in spatial correlation magnitudes can be attributed to the presence of rain-bearing systems countrywide in the rain season which influence rainfall generation.

Furthermore, the decline of correlation with distance for the monthly rainfall series after the first 20 km was more linear. In contrast, the individual months, seasonal and annual series had a more exponential decrease. All inter-station averaged correlations were positive despite the occurrence of some negative inter-station correlations. Local average maximum correlations can be observed in Fig. 4 at separation distances between 600 and 800 km. Only a few stations to the extreme north and south of Malawi are separated by those distances. On close examination, it was established that there was high correlation between Chitipa in the north and Fort Lister in the south, which affected the average correlation. These two are both high-altitude stations above 1,100 m and possibly experience similar rainfall generation conditions. Johnson (1962) and Jackson (1974), in their studies in East Africa, pointed out that such increases in spatial correlation can sometimes be a result of the occurrence of storm centres at constant distances apart within a general area of rain in a month. Apart from this isolated case of high correlations at large inter-station distances, it is evident in Fig. 4 that the highest spatial correlations can be accounted for in the first 100 km. Table 2 agrees with this observation where average spatial correlations were computed at first distance intervals of 0–20, 0–30, 0–50, 0–75 and 0–100 km. We therefore narrowed to the first 100 km by computing spatial correlations at 10-km intervals (Fig. 5). From Table 2 and Fig. 5, it is clear that only the monthly series have spatial correlations above +0.50 within the first 100 km. This suggests that rainfall in Malawi varies considerably even within short distances.

Table 2 Spatial correlations at various first averaging distances
Full size table
Fig. 5
figure 5

Spatial correlations for annual, monthly, March and August rainfall series in the first 100 km averaged at 10-km intervals

Full size image

Related studies with similar findings include Johnson (1962), Jackson (1972, 1974, 1978) and Sharon (1974) in East Africa; Mooley and Mohamed Ismail (1982) in India; and Sen and Habib (2001) in Turkey. Jackson (1978) highlighted that correlations between stations even 10 km apart can be surprisingly low in the tropics as compared to higher latitudes. For the accurate representation of rainfall observation in the tropics, inter-station correlation of +0.9 was recommended in previous studies (Jackson 1978). However, for the southeast of the USA, Baigorria et al. (2007) found stronger correlation for stations even as far as 600 km apart in January, whilst July showed similar correlations at only 200 km. Different atmospheric physics producing the rainfall was cited as the main reason for these differences.

4.2.3 Rainfall regimes of the annual, seasonal and monthly rainfall series

Annual rainfall series

Annual rainfall was characterised by high spatial variation countrywide. The country mean annual rainfall was 1,083 mm with mean inter-annual variability of 26%. The highest and lowest observed rainfall series are both to the south of the country. Table 3 is a summary of the statistics, and Fig. 6 shows the spatial patterns of the mean annual rainfall \( \left( {\overline R } \right) \) and the CVR.

Table 3 Monthly, annual, seasonal rainfall summary statistics
Full size table
Fig. 6
figure 6

Spatial distribution of annual rainfall in Malawi. a Mean annual rainfall (R) distribution. b Inter-annual rainfall variability (CVR)

Full size image

From Fig. 6, we can see that the highest annual rainfall was recorded to the southeast of the country. The statistics of Lujeri station, located in the southeastern highlands, showed that the station had the highest annual mean of 2,298.4 mm/year. Nchalo station located in the Lower Shire River Valley to the south of the country had the lowest mean annual rainfall 672 mm/year, about 71% difference. Mangochi rainfall station, along the Lake Malawi shore, had the highest inter-annual variability of 41%. Both Lujeri station in the southeastern highlands and Dowa station in the central region highlands had the lowest inter-annual variability at 18%. There was more spatial variability to the south of the country, although the high rainfall areas in the southeastern highlands seem to have had lower temporal variation. The central and northern parts of the country, however, exhibited lower inter-annual variability. The nature of the rainfall pattern in Malawi suggests that local factors like topography have a dominant role in the spatial distribution of rainfall. The actual role of such local factors was not further investigated in this study. However, our results in general agree with studies elsewhere, including those by De Luís et al. (2000) in Valencia region in Eastern Spain and Bewket and Conway (2007) in Ethiopia’s Amhara region. These also highlighted the role of topography on the rainfall pattern in those areas. In addition, areas with frequent occurrence of droughts and flood, for example the lower Shire area, had CVs higher than 30%.

Seasonal rainfall series

All the stations experience most of the rainfall in the main rainfall season months from November to April. This is the period in which the ITCZ is active in Malawi. From the data and Table 3, Lujeri station again had the highest rainfall in the main rainfall season of about 1,876 mm/year, whilst Nchalo had the lowest rainfall of 635.34 mm/year, a 66% difference. The pattern of spatial distribution was similar to the annual series. The mean rainfall for the dry season was rather low at 89.7 mm. Furthermore, the range of contributions for the dry season to the total annual rainfall was generally very low, from about 19% at Lujeri and Chitakale in the southern highlands to about 1% in the Chikwawa–Nchalo area of the Lower Shire plain. This is typical of highly seasonal rainfall regimes. Lujeri is in a very high rainfall area in the southern highlands, whilst Nchalo is located in Lower Shire River basin, a flood plain and one of the driest places in Malawi. The difference in the contributions can be attributed to the winter Chiperoni rainfall which is a very important contributor of the rainfall especially in the southeastern highland areas.

Monthly rainfall series

Monthly rainfall series showed various patterns of spatial variation. January accounts for the highest countrywide mean rainfall of 246 mm. The CVR for January was 43%. Most of the rains were concentrated between the months of December, January and February. Lowest mean rainfall for the months occurred in the dry season months of August and September and accounted for the largest CVR of over 239% (Table 3). Spatially, Lujeri station in the southeast highlands had the highest mean rainfall of 376 mm in January. In general, the highland areas to the north and southeast of the country had the highest monthly average rainfall. On the other hand, August and September were the driest months, both with a countrywide mean rainfall of 6 mm. During the dry season, most areas normally have no recorded rainfall, except for small patches of rainfall in the highlands. The high rainfall areas exhibited less inter-annual variation in all months, and January had the lowest CVR countrywide.

PCI and APCI series

Most of the stations had high to very high concentrations. This is an indication that intra-annual rainfall distribution was highly variable both temporally and spatially, as shown in Fig. 7a. There were no stations with a stable monthly rainfall regime (mean PCI <10). Twenty percent of the stations had high mean PCIs of between 11 and 20, with the rest having mean PCIs between 20 and 30. The pattern matches with the rainfall areas: Stations with the highest mean annual rainfall had relatively lower concentration indices, i.e. the southeastern highlands and northern highlands, whilst those with the highest concentration indices also had higher rainfall variability. This is expected because of the highly seasonal nature of the rainfall of the area and most of the rainfall is concentrated in a 3-month period between December and February. The coefficient of variability showing the inter-annual variability of the PCI ranges from a minimum of 11% to a maximum of 35% (Fig. 7b). The highest variability was again to the south, with pockets in the north and centre of the country showing high inter-annual variability.

Fig. 7
figure 7

Spatial distribution of precipitation concentration index (PCI) in Malawi. a Mean monthly PCI. b Inter-annual PCI variability (CVPCI)

Full size image

4.2.4 Trends in rainfall elements

Monthly series

Negative trends dominated the monthly series in both cases where the MK test was applied directly to the series or applying the SMK. Thirty-seven (88%) of the 42 stations showed a negative trend. Out of these 37 negative trends, only four of the stations—Chanco, Chitakale, Liwonde and Mangochi, all in the south—showed significant negative trends. On the other hand, only five stations showed positive trends, with only one station, Chikweo in the south, having a significant trend at the 5% significance level (Tables 4 and 5 and Fig. 8a). The spatial distribution of the trends was in a pattern where the centre and north had all negative trends, with all positives confined to the south, mixed with some negative trends. The countrywide rate of change of the monthly series was also mixed, with linear trends ranging from +2.38 to −1.51 mm/year. From the linear trends, the rainfall changed at an average of +0.21 mm/year in the south. There was, however, an even distribution of both negative and positive rates, indicating more localised changes in the rainfall. In the centre, the annual average rate of change was −0.39 mm/year, whilst the north experienced a decline with an average annual rate of change of −0.29 mm/year. The pattern of change is therefore clearer in the north and the centre than to the south of the country.

Table 4 Rainfall trends in Malawi as percentage (%) of the 42 stations
Full size table
Table 5 Summary of countrywide distribution of the rainfall trends for selected variables
Full size table
Fig. 8
figure 8

Mann–Kendall rainfall trends in Malawi for: monthly series (a); annual total (b); wet season total (c); and dry season total (d). Upward triangles represent positive trends and downward triangles represent negative trends. Trends significant at 5% level are shaded. Open circles represent no trends

Full size image

Annual rainfall

Annual rainfall series showed various temporal trends which can be characterised as heterogeneous. Fifty-two percent of the stations showed negative trends, and of these, two stations—Karonga in the north of the country and Chitakale in the high rainfall southeastern highlands—had significant negative trends at the 5% significance level. For the other 45% stations showing positive trends in the annual rainfall, only one station, Ngabu in the Lower Shire Valley area to the south of the country, showed a significant positive trend (Tables 4 and 5 and Fig. 8b). From the average of the linear trends, the country had an average rate of change of +1.03 mm/year. The linear trends further showed that rainfall decreased in the north and central parts of the country at average rates of −1.9 and −2.6 mm/year, respectively. The south on the other hand experienced increases at an average rate of +2.8 mm/year.

The wet season total rainfall showed similar trends to the annual trends pattern. Twenty-three stations showed negative trends. The negative trends were significant at Liwonde in the south and Karonga in the north. Positive trends were found at 18 of the stations, with only one station—Ngabu in the south—showing a significant positive trend (Tables 4 and 5 and Fig. 8c). Overall, negative trends slightly dominate, although most are not significant at the 5% significant level. Spatially, negative trends dominate in the central parts, whilst there was a mixed pattern of positive and negative trends to the north and south. Few stations in the south showed no trends at all. The countrywide average rate of change was −0.17 mm/year. The south of the country experienced an average rate of change of +1.18 mm/year. The annual rates of change in the centre and north of the country were −2.25 and −2.39 mm/year, respectively.

In the dry season totals, there were more negative trends countrywide (Tables 4 and 5 and Fig. 8d). Sixty-four percent of the stations had reduced dry season rainfall totals, and 14% percent of the negative trends were significant. Of the 36% stations with positive trends in the dry season, 2% of these positive trends were significant. The spatial distribution of the various trends did not show an obvious pattern in the south and centre of the country. More negative trends dominated in the extreme north of the country.

|AR| series

In the annual rainfall variability series, 32 stations (76%) showed positive trends, with three stations (7%) having significant positive trends: Makhanga and Mangochi in the South and Nkhotakota in the centre (Tables 4 and 5). On the other hand, nine stations showed negative trends, but none of which was significant at the 5% significance level. The countrywide distribution of the |AR| trends (figure not shown) was evidently dominated by the positive trends. This signifies that there was an increase in inter-annual variability of rainfall in the country.

Individual months’ series

Various trends were shown by each of the 12 subseries of the individual months from November to October (Table 4). Negative trends, not significant at the 5% significance level, were dominant for most of the months. Positive trends were, however, found for the months of January and February in 74% and 52% of the stations, respectively. In these 2 months with positive trends, 21% and 5% of the stations had significant positive trends. January and February are the peak months of the rain season. Based on the slope of the linear trends, the annual rates of change of rainfall for the individual months were, however, minimal. Spatially (figures not shown), we noted the following countrywide distributions for each of the months:

  • November: The central parts of Malawi were dominated by negative trends, whilst positive trends were dominant to the north and south of the country.

  • December: Negative trends were more evident in the central and part of the north of the country, whilst there was no definite pattern in south.

  • January: More positive trends were observed to the south and north of the country, with no obvious pattern in the centre.

  • February: More positive trends were spread evenly countrywide.

  • March: Negative trends dominated to the north, whilst positive trends dominated the centre and south of the country.

  • April–May–June: More negative trends were evenly distributed countrywide.

  • July: Negative trends in the centre and no definite pattern to the north and south of the country.

  • August–September–October: No obvious pattern of trends countrywide.

PCI series and |APCI| series

There were more positive trends in the rainfall concentration index (PCI). These positive trends were uniformly distributed countrywide. From Table 6, 39 stations (93%) showed positive trends, with 11 of the stations having significant trends: seven in the south (Balaka, Chanco, Chichiri, Chitakale, Mangochi, Mwanza and Nchalo); three stations in the centre (Dowa, Salima and Nkhotakota); and only Chitipa station in the north. Three stations, all in the south of the country, showed negative trends, none of which was significant. The spatial distribution pattern of the PCI trends was similar to the monthly series than the annual series (Fig. 9a).

Table 6 Summary of countrywide distribution of the PCI and series trends
Full size table
Fig. 9
figure 9

Mann–Kendall trends in: monthly precipitation concentration index (a) and absolute values of the PCI anomalies (series) (b). All symbols as in Fig. 8

Full size image

For the inter-annual variability of rainfall concentration index (|APCI|, no definite trend pattern was evident. Twenty-six stations had negative trends and 16 stations had positive trends, none of which was significant. De Luís et al. (2000) suggested that such a pattern is common for areas where local factors have a dominant role for the changes found (Table 6 and Fig. 9b).

5 Conclusions

This study investigated the spatial and temporal characteristics of various rainfall variables at 42 stations in Malawi. We highlight the following key points from the results of the study after basic data quality control and analysis:

  • Serial correlations for the monthly series, i.e. month-to-month series, were high. These series clearly showed a sinusoidal repetitive annual pattern at all observation stations owing to the seasonality of the climate.

  • The high spatial correlations in the month-to-month series can therefore be attributed to similar rainfall generation systems throughout the year.

  • Spatially, strong correlations at distances <20 km were found for the annual totals, seasonal totals (wet and dry) and the individual month’s totals. All series showed an abrupt decline in spatial correlation after the first 20 km. Our results agree with studies in similar tropical settings by Gregory (1965) in Jackson (1974) for Sierra Leone and Jackson (1972) for Tanzania. Such lower correlations normally are typical of most tropical areas where rainfall occur within fairy small convective storms than in the case of widespread rain experienced in higher latitudes (Jackson 1974). The results imply that a higher density of stations is required for the accurate observation of rainfall.

  • Temporally, most of the rainfall variables at the individual stations had no significant trends countrywide. The predominance of positive trends in the |AR| and |APCI|, however, suggests that there has been an increase in inter-annual and intra-annual rainfall variability rather than specific changes in the rainfall. This finding is similar to that by Nel (2009) for the KwaZulu–Natal Drakensberg region of South Africa. Month-to-month rainfall series were, however, dominated by negative but not significant trend to the north and centre of the country. A similar pattern in the annual and seasonal totals was identified. We observed that the pattern of change of the annual and seasonal rainfall is consistent with the country’s two climate divisions by Shongwe et al. (2006): one composed of the north and centre and the other composed of the south only. The negative trends identified agree with studies by Kampata et al. (2008) in the headwaters of the Zambezi River and Batisani and Yarnal (2010) for Botswana to the southwest of Malawi. In the individual monthly series, the months of January and February were dominated by positive trends, whilst the rest of the months exhibited negative trends. The January and February trends are in contrast with those from the study by Batisani and Yarnal (2010) for Botswana, whilst the rest of the months agree. Furthermore, monthly rainfall concentration (PCI) countrywide had increased, indicating increased variability within a year. However, there was also no definite pattern for the inter-annual variability of the monthly rainfall concentration (|CVPCI|).