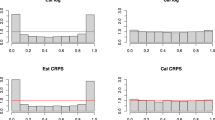
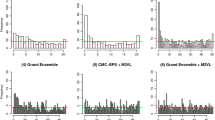
Abstract
Forecast ensembles are typically employed to account for prediction uncertainties in numerical weather prediction models. However, ensembles often exhibit biases and dispersion errors, thus they require statistical post-processing to improve their predictive performance. Two popular univariate post-processing models are the Bayesian model averaging (BMA) and the ensemble model output statistics (EMOS). In the last few years, increased interest has emerged in developing multivariate post-processing models, incorporating dependencies between weather quantities, such as for example a bivariate distribution for wind vectors or even a more general setting allowing to combine any types of weather variables. In line with a recently proposed approach to model temperature and wind speed jointly by a bivariate BMA model, this paper introduces an EMOS model for these weather quantities based on a bivariate truncated normal distribution. The bivariate EMOS model is applied to temperature and wind speed forecasts of the 8-member University of Washington mesoscale ensemble and the 11-member ALADIN-HUNEPS ensemble of the Hungarian Meteorological Service and its predictive performance is compared to the performance of the bivariate BMA model and a multivariate Gaussian copula approach, post-processing the margins with univariate EMOS. While the predictive skills of the compared methods are similar, the bivariate EMOS model requires considerably lower computation times than the bivariate BMA method.





Similar content being viewed by others
Notes
PEARP: Prévision d’Ensemble ARPege.
COSMO: Consortium for Small scale Modeling.
ALADIN: Aire Limitée Adaptation dynamique Development International.
ARPEGE: Action de Recherche Petite Echelle Grande Echelle.
References
Bao L, Gneiting T, Raftery AE, Grimit EP, Guttorp P (2010) Bias correction and Bayesian model averaging for ensemble forecasts of surface wind direction. Mon Weather Rev 138:1811–1821
Baran S (2014) Probabilistic wind speed forecasting using Bayesian model averaging with truncated normal components. Comput Stat Data Anal 75:227–238
Baran S, Lerch S (2015) Log-normal distribution based EMOS models for probabilistic wind speed forecasting. Q J R Meteorol Soc 141:2289–2299
Baran S, Möller A (2015) Joint probabilistic forecasting of wind speed and temperature using Bayesian model averaging. Environmetrics 26:120–132
Baran S, Horányi A, Nemoda D (2013) Statistical post-processing of probabilistic wind speed forecasting in Hungary. Meteorol Z 22:273–282
Baran S, Horányi A, Nemoda D (2014) Probabilistic temperature forecasting with statistical calibration in Hungary. Meteorol Atmos Phys 124:129–142
Bouallègue BZ, Theis S, Gebhardt C (2013) Enhancing COSMO-DE ensemble forecasts by inexpensive techniques. Meteorol Z 22:49–59
Buizza R, Tribbia J, Molteni F, Palmer T (1993) Computation of optimal unstable structures for a numerical weather prediction system. Tellus A 45:388–407
Buizza R, Houtekamer PL, Toth Z, Pellerin G, Wei M, Zhu Y (2005) A comparison of the ECMWF, MSC, and NCEP global ensemble prediction systems. Mon Wea Rev 133:1076–1097
Delle Monache L, Hacker JP, Zhou Y, Deng X, Stull RB (2006) Probabilistic aspects of meteorological and ozone regional ensemble forecasts. J Geophys Res 111:D24307
Dennis J, Schnabel R (1983) Numerical methods for unconstrained optimization and nonlinear equations. Prentice Hall, New Jersey
Descamps L, Labadie C, Joly A, Bazile E, Arbogast P, Cébron P (2015) PEARP, the Météo-France short-range ensemble prediction system. Q J R Meteorol Soc 141:1671–1685
Diebold FX, Mariano RS (1995) Comparing predictive accuracy. J Bus Econ Stat 13:253–263
Eckel FA, Mass CF (2005) Effective mesoscale, short-range ensemble forecasting. Wea Forecast 20:328–350
ECMWF Directorate (2012) Describing ECMWF’s forecasts and forecasting system. ECMWF Newsl 133:11–13
Fraley C, Raftery AE, Gneiting T (2010) Calibrating multimodel forecast ensembles with exchangeable and missing members using Bayesian model averaging. Mon Weather Rev 138:190–202
Fraley C, Raftery AE, Gneiting T, Sloughter JM, Berrocal VJ (2011) Probabilistic weather forecasting in R. R J 3:55–63
Fritz H, Filzmoser P, Croux C (2012) A comparison of algorithms for the multivariate \(L_1\)-median. Comput Stat 27:393–410
Gneiting T (2014) Calibration of medium-range weather forecasts. ECMWF Technical Memorandum No. 719. http://old.ecmwf.int/publications/library/ecpublications/ _pdf/tm/701-800/tm719. Accessed 27 July 2015
Gneiting T, Raftery AE (2005) Weather forecasting with ensemble methods. Science 310:248–249
Gneiting T, Raftery AE (2007) Strictly proper scoring rules, prediction and estimation. J Am Stat Assoc 102:359–378
Gneiting T, Raftery AE, Westveld AH, Goldman T (2005) Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estimation. Mon Weather Rev 133:1098–1118
Gneiting T, Stanberry LI, Grimit EP, Held L, Johnson NA (2008) Assessing probabilistic forecasts of multivariate quantities, with applications to ensemble predictions of surface winds (with discussion and rejoinder). Test 17:211–264
Grell GA, Dudhia J, Stauffer DR (1995) A description of the fifth-generation Penn state/NCAR mesoscale model (MM5). Technical note NCAR/TN-398+STR. National Center for Atmospheric Research, Boulder. http://nldr.library.ucar.edu/repository/assets/technotes/ TECH-NOTE-000-000-000-214. Accessed 27 July 2015
Horányi A, Kertész S, Kullmann L, Radnóti G (2006) The ARPEGE/ALADIN mesoscale numerical modeling system and its application at the Hungarian Meteorological Service. Időjárás 110:203–227
Horányi A, Mile M, Szűcs M (2011) Latest developments around the ALADIN operational short-range ensemble prediction system in Hungary. Tellus A 63:642–651
Lee G, Scott C (2012) EM algorithms for multivariate Gaussian mixture models with truncated and censored data. Comput Stat Data Anal 56:2816–2829
Leith CE (1974) Theoretical skill of Monte-Carlo forecasts. Mon Weather Rev 102:409–418
Lerch S, Thorarinsdottir TL (2013) Comparison of non-homogeneous regression models for probabilistic wind speed forecasting. Tellus A 65:21206
Leutbecher M, Palmer TN (2008) Ensemble forecasting. J Comput Phys 227:3515–3539
Milasevic P, Ducharme GR (1987) Uniqueness of the spatial median. Ann Stat 15:1332–1333
Möller A, Lenkoski A, Thorarinsdottir TL (2013) Multivariate probabilistic forecasting using ensemble Bayesian model averaging and copulas. Q J R Meteorol Soc 139:982–991
National Weather Service (1998) Automated Surface Observing System (ASOS) Users guide. http://www.weather.gov/asos/aum-toc. Accessed 27 July 2015
Nelder JA, Mead R (1965) A simplex algorithm for function minimization. Comput J 7:308–313
Pinson P (2012) Adaptive calibration of \((u, v)\)-wind ensemble forecasts. Q J R Meteorol Soc 138:1273–1284
Press WH, Teukolsky SA, Vetterling WT, Flannery BP (2007) Numerical recipes. The art of scientific computing, 3rd edn. Cambridge University Press, Cambridge
Raftery AE, Gneiting T, Balabdaoui F, Polakowski M (2005) Using Bayesian model averaging to calibrate forecast ensembles. Mon Weather Rev 133:1155–1174
Rosenbaum S (1961) Moments of a truncated bivariate normal distribution. J R Stat Soc Ser B 23:405–408
Schefzik R, Thorarinsdottir TL, Gneiting T (2013) Uncertainty quantification in complex simulation models using ensemble copula coupling. Stat Sci 28:616–640
Scheuerer M (2014) Probabilistic quantitative precipitation forecasting using ensemble model output statistics. Q J R Meteorol Soc 149:1086–1096
Schuhen N, Thorarinsdottir TL, Gneiting T (2012) Ensemble model output statistics for wind vectors. Mon Weather Rev 140:3204–3219
Sloughter JM, Gneiting T, Raftery AE (2010) Probabilistic wind speed forecasting using ensembles and Bayesian model averaging. J Am Stat Assoc 105:25–37
Sloughter JM, Gneiting T, Raftery AE (2013) Probabilistic wind vector forecasting using ensembles and Bayesian model averaging. Mon Weather Rev 141:2107–2119
Thorarinsdottir TL, Gneiting T (2010) Probabilistic forecasts of wind speed: ensemble model output statistics by using heteroscedastic censored regression. J R Stat Soc Ser A 173:371–388
Toth Z, Kalnay E (1997) Ensemble forecasting at NCEP and the breeding method. Mon Weather Rev 125:3297–3319
Vardi Y, Zhang CH (2000) The multivariate \(L_1\)-median and associated data depth. Proc Natl Acad Sci USA 97:1423–1426
Wilks DS (2011) Statistical methods in the atmospheric sciences, 3rd edn. Elsevier, Amsterdam
Williams RM, Ferro CAT, Kwasniok F (2014) A comparison of ensemble post-processing methods for extreme events. Q J R Meteorol Soc 140:1112–1120
Acknowledgments
An essential part of this work was made during the visit of Sándor Baran at the Heidelberg Institute for Theoretical Studies. The research stay in Heidelberg was funded by the DAAD program “Research Stays for University Academics and Scientists, 2015”. Sándor Baran was also supported by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences. The authors are indebted to Tilmann Gneiting for his useful suggestions and remarks, the University of Washington MURI group for providing the UWME data, Mihály Szűcs from the HMS for the ALADIN-HUNEPS data and Thordis Thorarinsdottir and Alex Lenkoski for their help with the R codes for the copula method. Last but not least, the authors are very grateful to the unknown reviewer for his/her valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: B. Ahrens.
Rights and permissions
About this article
Cite this article
Baran, S., Möller, A. Bivariate ensemble model output statistics approach for joint forecasting of wind speed and temperature. Meteorol Atmos Phys 129, 99–112 (2017). https://doi.org/10.1007/s00703-016-0467-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00703-016-0467-8