Mathematical model of perineural tumor spread: a pilot study

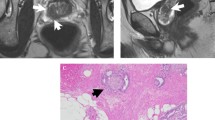
Abstract

Background

Perineural spread (PNS) of pelvic cancer along the lumbosacral plexus is an emerging explanation for neoplastic lumbosacral plexopathy (nLSP) and an underestimated source of patient morbidity and mortality. Despite the increased incidence of PNS, these patients are often times a clinical conundrum—to diagnose and to treat. Building on previous results in modeling glioblastoma multiforme (GBM), we present a mathematical model for predicting the course and extent of the PNS of recurrent tumors.

Methods

We created three-dimensional models of perineurally spreading tumor along the lumbosacral plexus from consecutive magnetic resonance imaging scans of two patients (one each with prostate cancer and cervical cancer). We adapted and applied a previously reported mathematical model of GBM to progression of tumor growth along the nerves on an anatomical model obtained from a healthy subject.

Results

We were able to successfully model and visualize perineurally spreading pelvic cancer in two patients; average growth rates were 60.7 mm/year for subject 1 and 129 mm/year for subject 2. The model correlated well with extent of PNS on MRI scans at given time points.

Conclusions

This is the first attempt to model perineural tumor spread and we believe that it provides a glimpse into the future of disease progression monitoring. Every tumor and every patient are different, and the possibility to report treatment response using a unified scale—as “days gained”—will be a necessity in the era of individualized medicine. We hope our work will serve as a springboard for future connections between mathematics and medicine.

Appendix 1

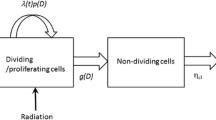
We adapted a mathematical model of GBM [27] to simulate PNS. The model is based on the Fisher-Kolmogorov equation (Eq. 1) [9],

$$ \frac{\partial c}{\partial t}=\nabla \left(D\left(\boldsymbol{x}\right)\nabla c\right)+\rho c\left(1-\frac{c}{K}\right) $$

(1)

where the solution variable c(x, t) represents the cancer cell density for spatial location x and time t. The parameters are the spatially varying invasion coefficient D, the proliferation rate ρ, and the carrying capacity of the tissue K. The spatial boundaries are given by the outer limits of the nerves. This is expressed in Eq. 2.

$$ D\left(\boldsymbol{x}\right)=\left\{\begin{array}{cc}D,& \boldsymbol{x}\in nerve\\ {}0,& otherwise\end{array}\right. $$

(2)

with the epineurium representing a no-flux boundary for the growth of the perineural cancer.

The initial conditions for each simulation take the form (Eq. 3),

$$ IC\left(\boldsymbol{x}\right)=\sum \limits_{i=0}^n{I}_0\exp \frac{{\left(\boldsymbol{x}-{\boldsymbol{\mu}}_{\boldsymbol{i}}\right)}^2}{2{\sigma}^2}, $$

(3)

for a total of n Gaussians, each with a center μ _i , standard deviation σ, and maximum population I ₀. Multiple Gaussians may be possible for multiple points of entry from the primary cancer. The number and placement of the initial conditions are approximated and multiple simulation instances performed. Consistent with previous results in modeling gliomas [27], we hold the carrying capacity at K = 108 cells/cm ³, initial condition maxima I ₀ = 0.0147 · K, and standard deviation σ = 3 mm.

As with previous studies on GBM growth [19, 27, 28], we assume that the observed velocity represents the asymptotically linear tumor progression of the T1Gd surface (Eq. 4),

$$ v=2\sqrt{D\rho}. $$

(4)

Unlike in previous work with brain cancer [4, 28], no relationship between the T2-weighted or FLAIR (fluid attenuation inversion recovery) signals and the population thresholds has been established in peripheral nervous system. This relationship is represented by the ratio λ = D/ρ, or the steepness of a population gradient between low cellular concentrations of the edema response and the high cellular concentration of the T1Gd. To address this, we assume a constant steepness in a numerically stable regime [16] (λ = 2). Choosing this constant value of λ gives numerical stability without the long establishment times of high diffusivity. Assuming limitless growth and the fixed steepness coefficient, the kinetic parameters can be calculated for each subject in terms of the velocity and the steepness (Eqs. 5 and 6),

$$ D=\frac{v\sqrt{\lambda }}{2} $$

(5)

$$ \rho =\frac{v}{2\sqrt{\lambda }} $$

(6)

For each subject, the “growth niduses” were selected based on anatomical points of entry to the lumbosacral plexus, i.e., where the autonomic nerves branch off the plexus.

Atlas creation

Much like atlases of the brain [8, 13], we created a digital atlas of the lumbosacral plexus from the T1Gd scan of a healthy female volunteer. The initial resolution of this scan being 0.7 × 0.7 × 1.0 mm. The segmented lumbosacral plexus is used as the medium in which the simulation evolves. This atlas is spatially refined to represent high resolution of growth. The boundary values apply at the dural edge of each nerve in digital representation.

Model implementation

Solutions to Eq. 1 are generated with a numerical diffusion-reaction solver employing a conjugate gradient method and backwards Euler algorithms written in Python. Each simulation is performed until the T1Gd volumetric radius is 25 mm. Thresholds representing T1Gd scans are tracked both volumetrically and spatially for further analysis.