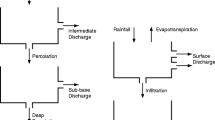
Abstract
This paper focuses on improving rainfall-runoff forecasts by a combination of genetic programming (GP) and basic hydrological modelling concepts. GP is a general optimisation technique for making an automated search of a computer program that solves some particular problem. The SORD! program was developed for the purposes of this study (in the R programming language). It is an implementation of canonical GP. Special functions are used for a combined approach of hydrological concepts and GP. The special functions are a reservoir model, a simple moving average model, and a cumulative sum and delay operator. The efficiency of the approach presented here is tested on runoff predictions for five catchments of various sizes. The input data consists of daily rainfall and runoff series. The forecast step is one day. The performance of the proposed approach is compared with the results of the artificial neural network model (ANN) and with the GP model without special functions. GP combined with these concepts provides satisfactory performance, and the simulations seem to be more accurate than the results of ANN and GP without these functions. An additional advantage of the proposed approach is that it is not necessary to determine the input lag, and there is better convergence. The SORD! program provides an easy-to-use alternative for data-oriented modelling combined with simple concepts used in hydrological modelling.






Similar content being viewed by others
References
Poli R, Langdon WB, McPhee NF (2008) A field guide to genetic programming. Published via http://lulu.com and freely available at http://www.gp-field-guide.org.uk (with contributions by Koza JR)
Koza JR (1992) Genetic Programming: on the programming of computers by means of natural selection. MIT Press, USA
Eiben AE, Smith JE (2003) Introduction to evolutionary computing. Springer, Berlin, p 320
Langdon WB, Poli R (2002) Foundations of genetic programming. Springer, Heidelberg
Bäck T, Fogel D, Michalewicz Z (2000) Evolutionary computation 1: basic algorithms and operators. Institute of Physics Publishing, Bristol
Babovic V (1996) Emergence, evolution, intelligence: hydroinformatics. PhD thesis, International Institute for Infrastructural, Hydraulic and Environmental Engineering and Technical University Delft, The Netherlands (Published by A. A. Balkema Publishers)
Babovic V, Abbott MB (1997) The evolution of equations from hydraulic data part i: theory. J Hydraul Res 35(3):397–430
Babovic V, Abbott MB (1997) Evolution of equations from hydraulic data. part ii: applications. J Hydraul Res 35(3):411–430
Cousin N, Savic DA (1997) A rainfall-runoff model using genetic programming. Technical report (report no. 97/03), School of Engineering, University of Exeter
Drecourt JP (1999) Application of neural networks and genetic programming to rainfall runoff modelling. Techical report, Danish Hydraulic Institute (D2K–0699-1)
Savic DA, Walters GA, Davidson JW (1999) A genetic programming approach to rainfall-runoff modelling. Water Resour Manag 13(3):219–231
Babovic V, Keijzer M (2002) Rainfall-runoff modelling based on genetic programming. Nordic Hydrol 33(5):331–346
Liong SY, Gautam RR, Khu ST, Babovic V, Keijzer M, Muttil N (2002) Genetic programming: a new paradigm in rainfall runoff modeling. J Am Water Resour Assoc 38(3):705–718
Jayawardena A, Muttil N, Fernando T (2005) Rainfall-runoff modelling using genetic programming. In: Zerger A, Argent R (eds) Proceedings of the MODSIM 2005 international congress on modelling and simulation: advances and applications for management and decision making. Melbourne, Australia, pp 1841–1847
Jayawardena AW, Muttil N, Lee JHW (2006) Comparative analysis of data-driven and gis-based conceptual rainfall-runoff model. J Hydrol Eng 11(1):1–11
Rabuñal JR, Puertas J, Suarez J, Rivero D (2007) Determination of the unit hydrograph of a typical urban basin using genetic programming and artificial neural networks. Hydrol Process 21(4):476–485
Makkeasorn A, Chang N, Zhou X (2008) Short-term streamflow forecasting with global climate change implications—a comparative study between genetic programming and neural network models. J Hydrol 352(3–4):336–354
Londhe S, Charhate S, Londhe S, Charhate S (2009) Towards modelling of streamflow using soft tools, vol 331. IAHS-AISH Publications, India, pp 245–253
Wang WC, Chau KW, Cheng CT, Qiu L (2009a) A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J Hydrol 374(3–4):294–306
Watanabe N, Fukami K, Imamura H, Sonoda K, Yamane S (2009) Flood forecasting technology with radar-derived rainfall data using genetic programming. In: Proceedings of the 2009 international joint conference on Neural Networks, IJCNN’09, IEEE Press, Piscataway, NJ, USA, pp 776–783
Ni Q, Wang L, Ye R, Yang F, Sivakumar M (2010) Evolutionary modeling for streamflow forecasting with minimal datasets: a case study in the West Malian river, China. Environ Eng Sci 27(5):377–385
Kashid S, Ghosh S, Maity R (2010) Streamflow prediction using multi-site rainfall obtained from hydroclimatic teleconnection. J Hydrol 395(1–2):23–38
Elshorbagy A, Corzo G, Srinivasulu S, Solomatine D (2010) Experimental investigation of the predictive capabilities of data driven modeling techniques in hydrology—part 1: concepts and methodology. Hydrol Earth Syst Sci 14(10):1931–1941
Elshorbagy A, Corzo G, Srinivasulu S, Solomatine D (2010) Experimental investigation of the predictive capabilities of data driven modeling techniques in hydrology—part 2: application. Hydrol Earth Syst Sci 14(10):1943–1961
Londhe S, Charhate S (2010) Comparison of data-driven modelling techniques for river flow forecasting. Hydrol Sci J 55(7):1163–1174
Maheswaran R, Khosa R (2011) Multi resolution genetic programming approach for stream flow forecasting. Lecture notes in computer science 7076 LNCS (part 1), pp 714–722
Rabuñal JR, Puertas J, Rivero D, Fraga I, Cea L, Garrido M (2011) Genetic programming for prediction of water flow and transport of solids in a basin. In: Proceedings of the 4th international conference on interplay between natural and artificial computation: new challenges on bioinspired applications, vol part II, IWINAC’11, Springer, Berlin, Heidelberg, pp 223–232
Whigham PA, Crapper PF (2001) Modelling rainfall-runoff using genetic programming. Math Comput Modell 33(6–7):707–721
Aytek A, Asce M, Alp M (2008) An application of artificial intelligence for rainfall-runoff modeling. J Earth Syst Sci 117(2):145–155
Guven A (2009) Linear genetic programming for time-series modelling of daily flow rate. J Earth Syst Sci 118(2):137–146
Fernando A, Shamseldin A, Abrahart R (2011) Comparison of two data-driven approaches for daily river flow forecasting. In: Proceedings of the MODSIM2011, 19th international congress on modelling and simulation, pp 1077–1083
Seckin N, Guven A (2012) Estimation of peak flood discharges at ungauged sites across Turkey. Water Resour Manag 26:2569–2581
Wang WC, Xu D, Qiu L, Ma J (2009b) Genetic programming for modelling long-term hydrological time series. Int Conf Nat Comput 4:265–269
Schaake J, Cong S, Duan Q (2006) US MOPEX data set. IAHS Publ Ser 307:9–28
R Development Core Team (2011) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org, ISBN: 3-900051-07-0
Nash J, Sutcliffe J (1970) River flow forecasting through conceptual models part i—a discussion of principles. J Hydrol 10(3):282–290
Luke S, Panait L (2002) Fighting bloat with nonparametric parsimony pressure. In: Proceedings of the 7th international conference on parallel problem solving from nature, PPSN VII, Granada, Spain, 7–11 Sept 2002, Springer, Berlin, pp 411–421
Kitanidis P, Bras R (1980) Real-time forecasting wih a conceptual hydrologic model. 2. Applications and results. Water Resour Res 16(6):1034–1044
Vladislavleva E, Smits G, den Hertog D (2010) On the importance of data balancing for symbolic regression. IEEE Trans Evolut Comput 14(2):252–277
Eggermont J, Hemert JIv (2001) Adaptive genetic programming applied to new and existing simple regression problems. In: Proceedings of the 4th European conference on genetic programming, EuroGP’01, Springer, Berlin, pp 23–35
Silva S, Almeida J (2003) Dynamic maximum tree depth-a simple technique for avoiding bloat in tree-based GP. In: Cantú-Paz E, Foster J, Deb K, Davis L, Roy R, O’Reilly UM, Beyer HG, Standish R, Kendall G, Wilson S, Harman M, Wegener J, Dasgupta D, Potter M, Schultz A, Dowsland K, Jonoska N, Miller J (eds) Genetic and evolutionary computation—GECCO 2003, lecture notes in computer science, vol 2724, Springer, Berlin/Heidelberg, pp 210–210
Havlíček V (2011) SORD!—GP tool for hydrological modelling. http://www.kvhem.cz/vyzkum/software/
Tukey JW (1977) Exploratory data analysis. Addison-Wesley, Reading, p 688
Acknowledgments
Financial support from the Technology Agency of the Czech Republic (research project TA02021249) is gratefully acknowledged. The authors wish to acknowledge the MOPEX project staff, which are associated with data providing and management.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Havlíček, V., Hanel, M., Máca, P. et al. Incorporating basic hydrological concepts into genetic programming for rainfall-runoff forecasting. Computing 95 (Suppl 1), 363–380 (2013). https://doi.org/10.1007/s00607-013-0298-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00607-013-0298-0