Abstract
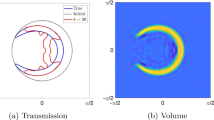
In recent years several new inverse scattering techniques have been developed that determine the boundary of an unknown obstacle by reconstructing the surrounding scattered field. In the case of sound soft obstacles, the boundary is usually found as the minimum contour of the total field. In this note we derive a different approach for imaging the boundary from the reconstructed fields based on a generalization of the eigenfunction expansion theorem. The aim of this alternative approach is the construction of higher contrast images than is currently obtained with the minimum contour approach.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Abramowitz, M and Stegun, I. A.: Handbook of mathematical functions, 9th ed. New York: Dover 1972.
Colton, D., Coyle, J., and Monk, P.: Recent developments in inverse scattering theory. SIAM Rev 42(3), 369–414 (2000).
Colton, D. and Kress, R.: Inverse acoustic and electromagnetic scattering theory, 2nd ed. Berlin: Springer 1998.
Colton, D. and Monk, P.: A novel method for solving the inverse scattering problem for time-harmonic waves in the resonance region. SIAM J. Appl. Math. 45, 1039–1053 (1985).
Colton, D. and Monk, P.: A novel method for solving the inverse scattering problem for time-harmonic waves in the resonance region II. SIAM J. Appl. Math. 46, 506–523 (1986).
Kirsch, A. and Kress, R.: A numerical method for an inverse scattering problem, in inverse problems (Engl and Groetsch, eds.), pp. 279–290. Orlando: Academic Press 1987.
Kress, R.: Integral equation methods in inverse acoustic and electromagnetic scattering, in boundary integral formulations for inverse analysis. In: (Ingham, D. B. Wrobel, L. C., eds.). South Hampton, UK: Computational Mechanics Publications 1997.
Leis, R.: Initial-boundary value problems in mathematical physics. Stuttgart: Teubner J. Wiley 1986.
Luke, D. R.: Multifrequency inverse obstacle scattering: the point source method and generalized filtered backprojection. Math. Comput. Simul. 66, 297–314 (2004).
Luke, D. R. and Potthast, R.: The no response test – a sampling method for inverse scattering problems. SIAM J. Appl. Math. 63(4), 1292–1312 (2003).
Potthast, R.: A fast new method to solve inverse scattering problems. Inverse Problems. 12, 731–742 (1996).
Potthast, R.: A point-source method for inverse acoustic and electromagnetic obstacle scattering problems. IMA J. Appl. Math. 61, 119–140 (1998).
Potthast, R.: Point sources and multipoles in inverse scattering theory. London: Chapman & Hall 2001.
Ramm, A. G.: Scattering by obstacles. Dordrecht: Reidel Publishing 1986.
Reed, M. and Simon, B.: Methods of modern mathematical physics III. Scattering theory. New York: Academic Press 1979.
Rose, J. H. and Cheney, M.: Generalized eigenfunction expansions for scattering in inhomogeneous three-dimensional media. J. Math. Phys. 29, 1347–1355 (1988).
Yosida, K.: Functional analysis, 2nd ed. Berlin: Springer 1968.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Luke, D. Image Synthesis for Inverse Obstacle Scattering Using the Eigenfunction Expansion Theorem. Computing 75, 181–196 (2005). https://doi.org/10.1007/s00607-004-0096-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00607-004-0096-9