Solution of Large Scale Algebraic Matrix Riccati Equations by Use of Hierarchical Matrices

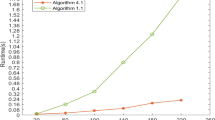
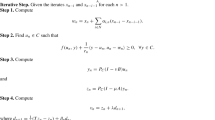In previous papers, a class of hierarchical matrices (ℋ-matrices) is introduced which are data-sparse and allow an approximate matrix arithmetic of almost optimal complexity. Here, we investigate a new approach to exploit the ℋ-matrix structure for the solution of large scale Lyapunov and Riccati equations as they typically arise for optimal control problems where the constraint is a partial differential equation of elliptic type. This approach leads to an algorithm of linear-logarithmic complexity in the size of the matrices.