Abstract
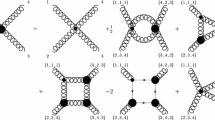
The quenched scalar Yukawa theory is solved in the light-front Tamm–Dancoff approach including up to four constituents (one scalar nucleon, three scalar pions). The Fock sector dependent renormalization is implemented. By studying the Fock sector norms, we find that the lowest two Fock sectors dominate the state even in the large-coupling region. The one-body sector shows convergence with respect to the Fock sector truncation. However, the four-body norm exceeds the three-body norm at the coupling \({\alpha \approx 1.7}\).
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bakker, B.L.G., et al.: Light-front quantum chromodynamics: a framework for the analysis of Hadron physics. Nucl. Phys. Proc. Suppl. 251–252, 165 (2014). [arXiv:1309.6333 [hep-ph]]
Perry R.J., Harindranath A.: Renormalization in the light-front Tamm–Dancoff approach to field theory. Phys. Rev. D 43, 4051 (1991)
Głazek S.D., Wilson K.G.: Renormalization of hamiltonians. Phys. Rev. D 48, 5863 (1993)
Paston, S.A., Franke, V.A.: Comparison of quantum field perturbation theory for the light front with the theory in Lorentz coordinates. Theor. Math. Phys. 112, 1117 (1997) [Teor. Mat. Fiz. 112, 399 (1997)]
Grangé P., Mathiot J.-F., Butet B., Werner W.: Taylor–Lagrange renormalization scheme: application to light-front dynamics. Phys. Rev. D 80, 105012 (2009)
Hiller, J.R., Brodsky, S.J.: Nonperturbative renormalization and the electron’s anomalous moment in large-α QED. Phys. Rev. D 59, 016006 (1998); [arXiv:hep-ph/9806541]
Karmanov, V.A., Mathiot, J.-F, Smirnov, A.V.: Systematic renormalization scheme in light-front dynamics with Fock space truncation. Phys. Rev. D 77, 085028 (2008); [arXiv:0801.4507 [hep-th]]
Karmanov V.A., Mathiot J.-F., Smirnov A.V.: Nonperturbative calculation of the anomalous magnetic moment in the Yukawa model within truncated Fock space. Phys. Rev. D 82, 056010 (2010)
Karmanov V.A., Mathiot J.-F., Smirnov A.V.: Ab initio nonperturbative calculation of physical observables in light-front dynamics: application to the Yukawa model. Phys. Rev. D 86, 085006 (2012)
Perry R.J., Harindranath A., Wilson K.G.: Light-front Tamm–Dancoff field theory. Phys. Rev. Lett. 65, 2959 (1990)
Carbonell, J., Desplanques, B., Karmanov, V.A., Mathiot, J.-F.: Explicitly covariant light-front dynamics and relativistic few-body systems. Phys. Rep. 300, 215 (1998); [arXiv:nucl-th/9804029]
Brodsky S.J., Hiller J.R., McCartor G.: Application of Pauli–Villars regularization and discretized light-cone quantization to a single-fermion truncation of Yukawa theory. Phys. Rev. D 64, 114023 (2001)
Baym, G.: Inconsistency of cubic Boson–Boson interactions. Phys. Rev. 117, 886 (1960)
Gross F., Şavklı C., Tjon J.: Stability of the scalar \({\chi^2\varphi}\) interaction. Phys. Rev. D 64, 076008 (2001)
Li, Y., Karmanov, V.A., Maris, P., Vary, J.P.: Ab initio approach to the non-perturbative scalar yukawa model. Phys. Lett. B
Wivoda J.J., Hiller J.R.: Application of discretized light-cone quantization to a model field theory in 3+1 dimensions. Phys. Rev. D 47, 4647 (1993)
Şavklı C., Tjon J., Gross F.: Feynman–Schwinger representation approach to nonperturbative physics. Phys. Rev. C 60, 055210 (1999); [arXiv:hep-ph/9906211]
Hwang, D.S., Karmanov, V.A.: Many-body fock sectors in Wick–Cutkosky model. Nucl. Phys. B 696, 413 (2004); [arXiv:hep-th/0405035]
Ji, C.-R., Tokunaga, Y.: Light-front dynamic analysis of bound states in a scalar field model. Phys. Rev. D 86, 054011 (2012); [arXiv:1205.3812 [nucl-th]]
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Li, Y., Karmanov, V.A., Maris, P. et al. Non-perturbative Calculation of the Scalar Yukawa Theory in Four-Body Truncation. Few-Body Syst 56, 495–501 (2015). https://doi.org/10.1007/s00601-015-0965-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00601-015-0965-0