Skip to main content
SpringerLink
Log in

Effect of Oblateness, Radiation and a Circular Cluster of Material Points on the Stability of Equilibrium Points in the Restricted Four-Body Problem

  • Published:
Few-Body Systems Aims and scope Submit manuscript

Abstract

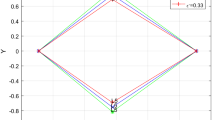
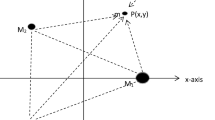
Within the framework of restricted four-body problem, we study the motion of an infinitesimal mass by assuming that the primaries of the system are radiating-oblate spheroids surrounded by a circular cluster of material points. In our model, we assume that the two masses of the primaries m 2 and m 3 are equal to μ and the mass m 1 is 1−2μ. By using numerical approach, we have obtained the equilibrium points and examined their linear stability. The effect of potential created by the circular cluster and oblateness coefficients for the more massive primary and the less massive primary, on the existence and linear stability of the libration point have been critically examine via numerical computation. The stability of these points examined shows that the collinear and the non-collinear equilibrium points are unstable. The result presented in this paper have practical application in astrophysics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Singh J., Taura J.J.: Effects of zonal harmonics and a circular cluster of material points on the stability of triangular equilibrium points in the R3BP. Astrophys. Space Sci. 350, 127 (2014)

    Article  ADS  Google Scholar 

  2. Singh J., Taura J.J.: Combined effect of oblateness, radiation and a circular cluster of material points on the stability of triangular liberation points in the R3BP. Astrophys Space Sci. 351, 499 (2014)

    Article  ADS  Google Scholar 

  3. Baltagiannis A.N., Papadakis K.E.: Families of periodic orbits in the restricted four-body problem. Astrophys. Space Sci. 336, 357 (2011)

    Article  ADS  MATH  Google Scholar 

  4. Kumari R., Kushvah B.S.: Stability regions of equilibrium points in restricted four-body problem with oblateness effects. Astrophys. Space Sci. 349, 693 (2014)

    Article  ADS  Google Scholar 

  5. Papadouris J.P., Papadakis K.E.: Equilibrium points in the photogravitational restricted four-body problem. Astrophys. Space Sci. 344, 21 (2013)

    Article  ADS  MATH  Google Scholar 

  6. Alvarez, M., Vidal C.: Dynamical aspects of an equilateral restricted four-body problem. Math. Prob. Eng. doi:10.1155/2009/181360

  7. Radzievskii V.V.: The restricted three-body problem including radiation pressure. Astron. J. 27, 250 (1950)

    MathSciNet  Google Scholar 

  8. Miyamoto M., Nagai R.: Three-dimensional models for the distribution of mass in galaxies. Publ. Astron. Soc. Jpn. 27, 533 (1975)

    ADS  Google Scholar 

  9. Peter I.D., Lissauer J.J.: Planetary Science. Cambridge University Press, New York (2001)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Applied Theoretical Physics Division, Department of Physics, Federal University Lafia, P. M. B. 146, Lafia, Nigeria

    Babatunde J. Falaye

Authors
  1. Babatunde J. Falaye
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Babatunde J. Falaye.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Falaye, B.J. Effect of Oblateness, Radiation and a Circular Cluster of Material Points on the Stability of Equilibrium Points in the Restricted Four-Body Problem. Few-Body Syst 56, 29–40 (2015). https://doi.org/10.1007/s00601-014-0922-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00601-014-0922-3

Keywords

Search

Navigation