Skip to main content

Advertisement

SpringerLink
Log in

Finite helical axes of motion are a useful tool to describe the three-dimensional in vitro kinematics of the intact, injured and stabilised spine

  • Original Article
  • Published:
European Spine Journal Aims and scope Submit manuscript

Abstract

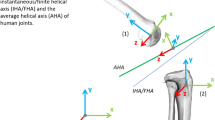
The finite helical-axes method can be used to describe the three-dimensional in vitro kinematics of the spine. However, this method still suffers from large stochastic calculation errors and poorly conceived visualisation techniques. The aim of the present study, therefore, was to improve the currently used finite helical axes description, by use of a less error-prone calculation algorithm and a new visualisation technique, and to apply this improved method to the study of the three-dimensional in vitro kinematics of the spine. Three-dimensional, continuous motion data of spinal motion segments were used to calculate the position and orientation of the finite helical axes (FHAs). The axes were then projected on plane antero-posterior, lateral and axial radiographs in order to depict the relation to the anatomy of each individual specimen. A hinge joint was used to estimate the measurement error of data collection and axes calculation. In an exemplary in vitro experiment, this method was used to demonstrate the ability of a prosthetic disc nucleus to restore the three-dimensional motion pattern of lumbar motion segments. In the validation experiment with the hinge joint, the calculated FHAs were lying within ±2.5 mm of the actual joint axis and were inclined relative to this axis at up to ±1.5°. In the exemplary in vitro experiment, the position and orientation of the FHAs of the intact specimens were subject to large inter-individual differences in all loading directions. Nucleotomy of the lumbar segments caused the axes to spread out, indicating complex coupled motions. The implantation of the prosthetic disc nucleus, for the most part, more than reversed this effect: the axes became oriented almost parallel to each other. The experiments showed that the present improved description of finite helical axes is a valid and useful tool to characterise the three-dimensional in vitro kinematics of the intact, injured and stabilised spine. The main advantage of this new method is the comprehensive visualisation of joint function with respect to the individual anatomy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4 a
Fig. 5 a

Similar content being viewed by others

References

  1. Chao EY (1980) Justification of triaxial goniometer for the measurement of joint rotation. J Biomech 13(12):989–1006

    CAS  PubMed  Google Scholar 

  2. Chau T (2001) A review of analytical techniques for gait data. Part 2: neural network and wavelet methods. Gait Posture 13(2):102–120

    Article  CAS  PubMed  Google Scholar 

  3. Cheze L, Fregly BJ, Dimnet J (1998) Determination of joint functional axes from noisy marker data using the finite helical axis. Hum Mov Sci 17:1–15

    Article  Google Scholar 

  4. Crawford NR (2002) A sequence of two rotations—50 degrees torso flexion followed by +/-120 degrees of head axial rotation—was monitored using (essentially) goniometers and simultaneously measured by Euler XZY an YZX decompositions of marker data from an electromagnetic system (flock of birds). Clin Biomech (Bristol, Avon) 17(2):166–168; author reply, 169

    Google Scholar 

  5. Cripton PA, Sati M, Orr TE, Bourquin Y, Dumas GA, Nolte LP (2001) Animation of in vitro biomechanical tests. J Biomech 34(8):1091–1096

    Article  CAS  PubMed  Google Scholar 

  6. Eysel P, Rompe J, Schoenmayr R, Zoellner J (1999) Biomechanical behaviour of a prosthetic lumbar nucleus. Acta Neurochir (Wien) 141(10):1083–1087

    Google Scholar 

  7. Goel VK, Winterbottom JM (1991) Experimental investigation of three-dimensional spine kinetics. Determination of optimal placement of markers. Spine 16(8):1000–1002

    CAS  PubMed  Google Scholar 

  8. Grassmann S, Oxland TR, Gerich U, Nolte LP (1998) Constrained testing conditions affect the axial rotation response of lumbar functional spinal units. Spine 23(10):1155–1162

    Article  CAS  PubMed  Google Scholar 

  9. Haher TR, O’Brien M, Felmly WT et al (1992) Instantaneous axis of rotation as a function of the three columns of the spine. Spine [Suppl 6] 17:S149-154

    Google Scholar 

  10. Marin F, Mannel H, Claes L, Durselen L (2003) Correction of axis misalignment in the analysis of knee rotations. Hum Mov Sci 22(3):285–296

    Article  CAS  PubMed  Google Scholar 

  11. Nagerl H, Kubein-Meesenburg D, Cotta H, Fanghanel J, Rossow A, Spiering S (1995) [Biomechanical principles in diarthroses and synarthroses. IV: the mechanics of lumbar vertebrae. A pilot study]. Z Orthop Ihre Grenzgeb 133(6):481–491

    CAS  PubMed  Google Scholar 

  12. Osterbauer PJ, Derickson KL, Peles JD, DeBoer KF, Fuhr AW, Winters JM (1992) Three-dimensional head kinematics and clinical outcome of patients with neck injury treated with spinal manipulative therapy: a pilot study. J Manipulative Physiol Ther 15(8):501–511. Erratum in (1992) J Manipulative Physiol Ther 15(9):following table of contents

    Google Scholar 

  13. Osterbauer PJ, Long K, Ribaudo TA et al (1996) Three-dimensional head kinematics and cervical range of motion in the diagnosis of patients with neck trauma. J Manipulative Physiol Ther 19(4):231–237

    PubMed  Google Scholar 

  14. Oxland TR, Panjabi MM, Lin RM (1994) Axes of motion of thoracolumbar burst fractures. J Spinal Disord 7(2):130–138

    CAS  PubMed  Google Scholar 

  15. Panjabi M, White AA 3rd (1971) A mathematical approach for three-dimensional analysis of the mechanics of the spine. J Biomech 4(3):203–211

    Article  CAS  PubMed  Google Scholar 

  16. Panjabi MM, Krag MH, Goel VK (1981) A technique for measurement and description of three-dimensional six degree-of-freedom motion of a body joint with an application to the human spine. J Biomech 14(7):447–460

    CAS  PubMed  Google Scholar 

  17. Ramsey DK, Wretenberg PF (1999) Biomechanics of the knee: methodological considerations in the in vivo kinematic analysis of the tibiofemoral and patellofemoral joint. Clin Biomech (Bristol, Avon) 14(9):595–611

    Google Scholar 

  18. Veldpaus FE, Woltring HJ, Dortmans LJ (1988) A least-squares algorithm for the equiform transformation from spatial marker co-ordinates. J Biomech 21(1):45–54

    CAS  PubMed  Google Scholar 

  19. White AA, Panjabi MM (1990) Clinical Biomechanics of the Spine, 2nd edn. Lippincott, Philadelphia

  20. Wilke HJ, Claes L, Schmitt H, Wolf S (1994) A universal spine tester for in vitro experiments with muscle force simulation. Eur Spine J 3(2):91–97

    CAS  PubMed  Google Scholar 

  21. Wilke HJ, Kavanagh S, Neller S, Haid C, Claes LE (2001) Effect of a prosthetic disc nucleus on the mobility and disc height of the L4–5 intervertebral disc postnucleotomy. J Neurosurg [Suppl2] 95:208–214

    Google Scholar 

  22. Winters JM, Peles JD, Osterbauer PJ, Derickson K, Deboer KF, Fuhr AW (1993) Three-dimensional head axis of rotation during tracking movements. A tool for assessing neck neuromechanical function. Spine 18(9):1178–1185

    CAS  PubMed  Google Scholar 

  23. Woltring HJ, Huiskes R, de Lange A, Veldpaus FE (1985) Finite centroid and helical axis estimation from noisy landmark measurements in the study of human joint kinematics. J Biomech 18(5):379–389

    Article  CAS  PubMed  Google Scholar 

  24. Woltring HJ, Long K, Osterbauer PJ, Fuhr AW (1994) Instantaneous helical axis estimation from 3-D video data in neck kinematics for whiplash diagnostics. J Biomech 27(12):1415–1432

    Article  CAS  PubMed  Google Scholar 

  25. Wu G, Siegler S, Allard P et al (2002) ISB recommendation on definitions of joint coordinate system of various joints for the reporting of human joint motion—part I: ankle, hip, and spine. International Society of Biomechanics. J Biomech 35(4):543–548

    Article  PubMed  Google Scholar 

Download references

Acknowledgment

The authors would especially like to thank Raymedica Inc. (Minneapolis, MN, USA) for the supply of their implants.

Author information

Authors and Affiliations

  1. Institute for Orthopedic Research and Biomechanics, University of Ulm, Helmholtzstraße 14, 89081 , Ulm, Germany

    A. Kettler, F. Marin, G. Sattelmayer, M. Mohr, H. Mannel, L. Dürselen, L. Claes & H. J. Wilke

Authors
  1. A. Kettler
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. F. Marin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. G. Sattelmayer
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. Mohr
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. H. Mannel
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. L. Dürselen
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. L. Claes
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. H. J. Wilke
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. J. Wilke.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kettler, A., Marin, F., Sattelmayer, G. et al. Finite helical axes of motion are a useful tool to describe the three-dimensional in vitro kinematics of the intact, injured and stabilised spine. Eur Spine J 13, 553–559 (2004). https://doi.org/10.1007/s00586-004-0710-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00586-004-0710-8

Keywords

Search

Navigation