Skip to main content
SpringerLink
Log in

On a front evolution in porous media with a source–analysis and numerics

  • Published:
Bulletin of the Brazilian Mathematical Society, New Series Aims and scope Submit manuscript

Abstract

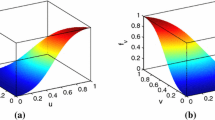
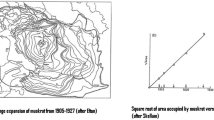
We analyze evolution of the interface between immiscible fluids of different densities in porous media. The fluids can be compressible (CO 2 or natural gases) or incompressible (oil, water). We rigorously prove that, if the heavier fluid is on the top and there are no sink or source, a tip of the interface will move in the direction of the gravity (if the tip is directed toward the bottom) or the buoyancy (if the tip is directed toward the top).We also showhowthe sink/source influence propagation of the interface and provide numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G. I. Barenblatt. Scaling, self-similarity, and intermediate asymptotic. Cambridge University Press, Cambridge (1996).

    Book  MATH  Google Scholar 

  2. V. G. Danilov and G. O. Omelyanov. Dynamics of the interface between two immiscible liquids with nearly equal densities under gravity. European Journal of AppliedMathematics, 13 (2002), 497–516.

    MathSciNet  MATH  Google Scholar 

  3. M. A. Hesse, H. A. Tchelepi, B. J. Cantwell and F. M. Orr Jr. Gravity currents in horizontal porous layers: transition from early to late self-similarity. J. Fluid. Mech., 577 (2007), 363–383.

    Article  MathSciNet  MATH  Google Scholar 

  4. H. Kalisch, D. Mitrovic and J. M. Nordbotten. Rayleigh-Taylor instability of immiscible fluids in porous media. Continuum Mech. Thermodyn. DOI 10. 1007/ s00161-014-0408z.

  5. L. Lake. Enhanced oil recovery. Prentice Hall, Englewood Cliffs (1989).

    Google Scholar 

  6. D. Mitrovic, J. M. Nordbotten and H. Kalisch, Dynamics of the interface between immiscible liquids of different densities with low Froude number. Nonlinear Anal. Real World Appl., 15 (2014), 361–366.

    Article  MathSciNet  MATH  Google Scholar 

  7. D. Mitrovic and A. Novak. Two-Phase Nonturbulent Flow with Applications. Mathematical Problems in Engineering, 2015 (2015), Article ID 439704, 8 pages.

    Google Scholar 

  8. J. M. Nordbotten, M. A. Celia and S. Bachu. Analytical solutions for leakage rates through abandoned wells. Water Resources Res., 40 (2004),W04204.

    Article  Google Scholar 

  9. R. Temam. Navier-Stokes equations. AMS Chelsea publishing (2000).

    MATH  Google Scholar 

  10. R. LeVeque. Numericalmethods for conservation laws. Vol. 132. Basel: Birkhäuser (1992).

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Science, Department of Mathematics, University of Zagreb, Bijenička cesta 30, 10000, Zagreb, Croatia

    Maroje Marohnić & Darko Mitrović

  2. Faculty of Mathematics, University of Montenegro, Cetinjski put bb, 81000, Podgorica, Montenegro

    Darko Mitrović

  3. Faculty of Electrical Engineering and Computing, University of Zagreb, Unska 3, 10000, Zagreb, Croatia

    Andrej Novak

Authors
  1. Maroje Marohnić
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Darko Mitrović
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Andrej Novak
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Andrej Novak.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Marohnić, M., Mitrović, D. & Novak, A. On a front evolution in porous media with a source–analysis and numerics. Bull Braz Math Soc, New Series 47, 521–532 (2016). https://doi.org/10.1007/s00574-016-0166-6

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00574-016-0166-6

Keywords

Mathematical subject classification

Search

Navigation