Numerical investigation into dynamic behavior of electrostatically-actuated circular clamped micro-plate subject to squeeze-film damping effect

Abstract

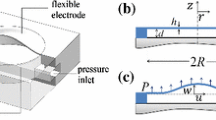
The analysis of electrostatically-actuated MEMS devices is complicated since structural deformation alters the nonlinear electrostatic force, which in turn redistributes and modifies the electrostatic coupling effect. The analysis is further complicated by the nonlinear squeeze-film damping effect exerted by the air film between the deformable diaphragm and the fixed substrate. Accordingly, the present study performs a numerical investigation into the effect of this squeeze-film damping phenomenon on the dynamic behavior of a MEMS device incorporating a circular clamped micro-plate. The deflection behavior of the micro-plate is described using an analytical model based on a linearized isothermal compressible Reynolds equation and a sealed pressure boundary condition. In performing the simulations, the model is solved using a hybrid differential transformation and finite difference scheme. The simulations focus specifically on the effects of the residual stress, actuation voltage and excitation frequency on the dynamic response of the membrane.

Appendix

Elementary symbol table

Symbol	Parameters
$A^{*}$	Dimensionless parameter
$b$	Width of beam
$D$	Flexural rigidity of the plate
$E$	Young’s modulus
$G$	Initial gap
$H$	Time interval
$\bar{H}$	Dimensionless distance between the gap
$h$	Thickness of the micro-plate
$h_{p}$	Variable distance between the gap ($h_{p} = G - u$)
$K_{n}$	Knudsen number (${\lambda \mathord{\left/ {\vphantom {\lambda {h_{p} }}} \right. \kern-0pt} {h_{p} }}$)
$P$	Absolute pressure
$P_{a}$	Ambient pressure
$P_{p}$	Net pressure ($P_{p} = P - P_{a}$)
$\bar{P}$	Dimensionless pressure
$Q^{*}$	Dimensionless parameter
$R$	Radius of the micro-plate
$\bar{r}$	Dimensionless radial distance
$T$	Differential transformation operation
$T$	Differential transformation operation
$\bar{T}$	Dimensionless time
$T_{r}^{*}$	Dimensionless parameter
$t$	Time
$U$	Differential transformed function of $\bar{u}$
$u$	Transverse deflection
$\bar{u}$	Dimensionless deflection
$V_{DC}$	The DC voltage
$V_{AC}$	The AC voltage
Greek symbols
$\theta$	Polar coordinate
$\omega$	Excitation frequency
$\bar{\omega }$	Dimensionless frequency
$\lambda$	The molecular mean free path length
$\mu$	Effective viscosity
$\mu_{0}$	Absolute viscosity
$\upsilon$	Poisson’s Ration
$\rho$	Density
$\varepsilon_{0}$	Permittivity of free space
$\sigma$	Squeeze number