Squeeze-film effects in MEMS devices with perforated plates for small amplitude vibration

Abstract

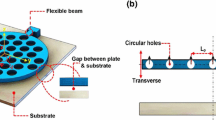
Squeeze-film effects of perforated plates for small amplitude vibration are analyzed through modified Reynolds equation (MRE). The analytical analysis reckons in most important influential factors: compressibility of the air, border effects, and the resistance caused by vertical air flow passing through perforated holes. It is found that consideration of air compressibility is necessary for high operating frequency and small ratio of the plate width to the attenuation length. The analytical results presented in this paper agree with ANSYS simulation results better than that under the air incompressibility assumption. The analytical analysis can be used to estimate the squeeze-film effects causing damping and stiffness added to the system. Since the value of Reynolds number involved in this paper is low (< 1), inertial effects are neglected.

Appendix A. Nomenclatures

a :

plate half width

b :

plate half length

d ₀ :

initial air gap

h :

plate thickness

h _eff :

effective plate thickness

l :

attenuation length

p :

squeeze-film pressure

p _a :

ambient pressure

p _h :

pressure caused by horizontal air flow

p _v :

pressure caused by vertical air flow

A _R :

aspect ratio

C :

damping coefficient

P _D :

dimensionless damping force

P _S :

dimensionless spring force

K :

stiffness coefficient

K _n :

Knudsen number

${\bar{P}_{\rm D}}$ :

dimensionless damping pressure

${\bar{P}_{\rm S}}$ :

dimensionless spring pressure

Q _z :

penetrating rate

R _i :

inner radius of the pressure cell

R _o :

outer radius of the pressure cell

β:

inner radius to outer radius ratio

ɛ₀ :

dimensionless vibration amplitude

μ:

air viscosity coefficient

μ_eff :

effective air viscosity coefficient

ρ:

air density

σ:

squeeze number

ω:

operating frequency in radians per second