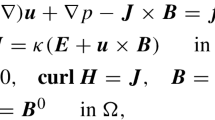Abstract
The paper deals with the homogenization of a magneto-elastodynamics equation satisfied by the displacement \(u_\varepsilon \) of an elastic body which is subjected to an oscillating magnetic field \(B_\varepsilon \) generating the Lorentz force \(\partial _t u_\varepsilon \times B_\varepsilon \). When the magnetic field \(B_\varepsilon \) only depends on time or on space, the oscillations of \(B_\varepsilon \) induce an increase of mass in the homogenized equation. More generally, when the magnetic field is time-space dependent through a uniformly bounded component \(G_\varepsilon (t,x)\) of \(B_\varepsilon \), besides the increase of mass the homogenized equation involves the more intricate limit g of \(\partial _t u_\varepsilon \times G_\varepsilon \) which turns out to be decomposed in two terms. The first term of g can be regarded as a nonlocal Lorentz force the range of which is limited to a light cone at each point (t, x). The cone angle is determined by the maximal velocity defined as the square root of the ratio between the elasticity tensor spectral radius and the body mass. Otherwise, the second term of g is locally controlled in \(L^2\)-norm by the compactness default measure of the oscillating initial energy.
Similar content being viewed by others
References
Bakhvalov, N., Panasenko, G.: Homogenisation: averaging processes in periodic media. Mathematical problems in the mechanics of composite materials, translated from the Russian by D. Leǐtes, Mathematics and its Applications (Soviet Series) 36, Kluwer Academic Publishers Group, Dordrecht, 1989, pp. 402 (1989)
Bardzokas, D.I., Filshtinsky, M.L., Filshtinsky, L.A.: Mathematical Methods in Electro-Magneto-Elasticity, Lecture Notes in Appl. and Compt. Mech. 32, Springer 2007, pp. 530 (2007)
Bensoussan, A., Lions, J.-L., Papanicolaou, G.: Asymptotic analysis for periodic structures, corrected reprint of the 1978 original, p. 398. AMS Chelsea Publishing, Providence, RI (2011)
Brahim-Otsmane, S., Francfort, G., Murat, F.: Homogenization in thermoelasticity, random media and composites. In: Proceedings of SIAM Workshop, Leesburg/VA (USA) 1988, 13–45 (1989)
Braides, A., Defranceschi, A.: Homogenization of multiple integrals, Oxford Lecture Series in Mathematics and its Applications 12, p. 312. The Clarendon Press, Oxford University Press (1998)
Brezis, H.: Functional Analysis, p. 599. Springer, New York Dordrecht Heidelberg London, Sobolev Spaces and Partial Differential Equations (2011)
Briane, M., Gérard, P.: A drift problem revisited. Ann. Scu. Nor. Sup. Pisa Cl. Sci. 11(5), 1–39 (2012)
Brinkman, H.C.: A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. A1, 27–34 (1947)
Casado-Díaz, J., Couce-Calvo, J., Maestre, F., Martín-Gómez, J.D.: Homogenization and correctors for the wave equation with periodic coefficients. Math. Mod. Meth. Appl. Sci. 24, 1343–1388 (2014)
Dal Maso, G.: An introduction to \(\Gamma \)-convergence, Progress in Nonlinear Differential Equations and their Applications 8, p. 354. Birkhaüser Boston Inc., Boston MA (1993)
Dunford, N., Schwartz, J.: Linear Operators, Part 1: General Theory, p. 861. Interscience publishers, New York (1957)
Evans, L.C.: Weak convergence methods for nonlinear partial differential equations, CBMS Regional Conference Series in Mathematics 74, published for the Conference Board of the Mathematical Sciences, Washington DC, by the American Mathematical Society, Providence RI, pp. 88 (1990)
Francfort, G.A., Murat, F.: Oscillations and energy densities in the wave equation. Comm. Partial Diff. Eq. 17, 1785–1865 (1992)
Khruslov, E.Ya.: “Homogenized models of composite media”, composite media and homogenization theory. Dal Maso, G. and Dell’Antonio, G.F. (eds.) Progress in Nonlinear Differential Equations and Their Applications, Birkhaüser, 159–182 (1991)
Lions, J.L., Magenes, E.: Problèmes Aux Limites Non Homogènes et Applications, (French) Travaux et Recherches Mathématiques 17, p. 372. Dunod, Paris (1968)
Lions, J.-L., Magenes, E.: Non-homogeneous boundary value problems and applications. Vol. I, Translated from the French. In: Kenneth, P. (ed.) Die Grundlehren der mathematischen Wissenschaften, Band 181, Springer, New York-Heidelberg, 1972, pp. 373 (1972)
Milton, G.W., Willis, J.: On modifications to Newton’s second law and linear continuum elastodynamics. Proc. R. Soc. Lond. Ser. A, Math. Phys. Eng. Sci. 463(2079), 855–880 (2007)
Murat, F.: “\(H\)-convergence”, Séminaire d’Analyse Fonctionnelle et Numérique, 1977-78, Université d’Alger, multicopied, 34 pp. English translation : F. Murat & L. Tartar, “H-convergence”, Topics in the Mathematical Modelling of Composite Materials. In: Cherkaev, L. and Kohn, R.V. (eds.) Progress in Nonlinear Differential Equations and their Applications, 31, Birkaüser, Boston, 21–43 (1998)
Sánchez-Palencia, E.: Nonhomogeneous Media and Vibration Theory. Lecture Notes in Physics, vol. 127. Springer, Berlin-New York (1980)
Spagnolo, S.: Sulla convergenza di soluzioni di equazioni paraboliche ed ellittiche. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 22(3), 571–597 (1968)
Tartar, L.: Homogénéisation en hydrodynamique. In: Singular Perturbation and Boundary Layer Theory. Lecture Notes in Mathematics, vol. 597. Springer, Berlin-Heidelberg (1977)
Tartar, L.: Remarks on homogenization. In: Homogenization and Effective Moduli of Materials and Media, IMA Vol. Math. Appl., 1, Springer, New-York 1986, 228–246 (1986)
Tartar, L.: The general theory of homogenization. In: A Personalized Introduction, Lecture Notes of the Unione Matematica Italiana 7, Springer, Berlin, UMI Bologna, 2009, pp. 492 (2009)
Acknowledgements
The authors wish to thank the unknown referee for his/her very careful reading of the paper, and for several relevant comments which have clarified some proofs. The second author also thanks the Université Rennes 1 and the Institut de Recherche Mathématique de Rennes for their invitation during his stay between June 25th and July 8th 2017, for the starting of this work. This paper has been partially supported by Project MTM2017 of the Ministerio de Ciencia, Innovación y Universidades of Spain.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Malchiodi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Briane, M., Casado-díaz, J. Increase of mass and nonlocal effects in the homogenization of magneto-elastodynamics problems. Calc. Var. 60, 163 (2021). https://doi.org/10.1007/s00526-021-02027-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-021-02027-0