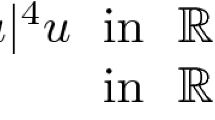Skip to main content
SpringerLink
Log in

On the Aleksandrov–Bakelman–Pucci estimate for the infinity Laplacian

  • Published:
Calculus of Variations and Partial Differential Equations Aims and scope Submit manuscript

Abstract

We prove L ∞ bounds and estimates of the modulus of continuity of solutions to the Poisson problem for the normalized infinity and p-Laplacian, namely

$$\begin{array}{ll} -\Delta_p^N u=f\quad{\rm for } \; n < p \leq\infty.\end{array}$$

We are able to provide a stable family of results depending continuously on the parameter p. We also prove the failure of the classical Alexandrov–Bakelman–Pucci estimate for the normalized infinity Laplacian and propose alternate estimates.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Argiolas R., Charro F., Peral I.: On the Aleksandrov–Bakel’man–Pucci estimate for some elliptic and parabolic nonlinear operators. Arch. Ration. Mech. Anal. 202(2), 875–917 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  2. Armstrong S., Smart C.: A finite difference approach to the infinity Laplace equation and tug-of-war games. Trans. Am. Math. Soc. 364(2), 595–636 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  3. Beckenbach, E., Bellman, R.: Inequalities, Ergebnisse der Mathematik und ihrer Grenzgebiete, N. F., Bd. 30. Springer, Berlin (1961)

  4. Bhattacharya T., DiBenedetto E., Manfredi J.: Limit as p → ∞ of Δ p u p  = f and related extremal problems. Rend. Sem. Mat. Univ. Politec. Torino 1986, 15–68 (1991)

    MathSciNet  Google Scholar 

  5. Birindelli, I., Demengel, F.: The Dirichlet problem for singular fully nonlinear operators. Discrete Contin. Dyn. Syst. Dynamical Systems and Differential Equations. Proceedings of the 6th AIMS International Conference, Poitiers, suppl., pp. 110–121 (2007)

  6. Cabré, X., Caffarelli, L.A.: Fully Nonlinear Elliptic Equations. American Mathematical Society Colloquium Publications, vol. 43. American Mathematical Society, Providence (1995)

  7. Crandall M.G., Evans L.C., Gariepy R.F.: Optimal Lipschitz extensions and the infinity Laplacian. Calc. Var. Partial Differ. Equ. 13(2), 123–139 (2001)

    MathSciNet  MATH  Google Scholar 

  8. Crandall M.G., Ishii H., Lions P.L.: User’s guide to viscosity solutions of second order partial differential equations. Bull. Am. Math. Soc. 27(1), 1–67 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  9. Dávila G., Felmer P., Quaas A.: Alexandroff–Bakelman–Pucci estimate for singular or degenerate fully nonlinear elliptic equations. C. R. Math. Acad. Sci. Paris 347(19–20), 1165–1168 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. Evans L.C., Gariepy R.F.: Measure Theory and Fine Properties of Functions. Studies in Advanced Mathematics. CRC Press, Boca Raton (1992)

    Google Scholar 

  11. Federer, H.: Geometric Measure Theory. Die Grundlehren der mathematischen Wissenschaften, Band 153. Springer, New York (1969)

  12. Giga, Y.: Surface Evolution Equations. A Level Set Approach, Monographs in Mathematics, vol. 99. Birkhäuser, Basel (2006)

  13. Gilbarg D., Gariepy N.S.: Elliptic Partial Differential Equations of Second Order. Springer, New York (1983)

    Book  MATH  Google Scholar 

  14. Gutierrez C.: The Monge–Ampère Equation. Birkhäuser, Basel (2001)

    Book  MATH  Google Scholar 

  15. Imbert C.: Alexandroff–Bakelman–Pucci estimate and Harnack inequality for degenerate/singular fully non-linear elliptic equations. J. Differ. Equ. 250(3), 1553–1574 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  16. Jensen R.: Uniqueness of Lipschitz extensions: minimizing the sup norm of the gradient. Arch. Ration. Mech. Anal. 123, 51–74 (1993)

    Article  MATH  Google Scholar 

  17. Kawohl B., Manfredi Juan J., Parviainen M.: Solutions of nonlinear PDEs in the sense of averages. J. Math. Pure Appl. 97(2), 173–181 (2012)

    MATH  Google Scholar 

  18. Krylov, N.V., Safonov, M.V.: An estimate for the probability of a diffusion process hitting a set of positive measure. Dokl. Akad. Nauk. SSSR 245(1), 18–20 (1979) (in Russian)

    Google Scholar 

  19. Krylov, N.V., Safonov, M.V.: A certain property of solutions of parabolic equations with measurable coefficients. Dokl. Akad. Nauk. SSSRIzv. Akad. Nauk. SSSR Ser. Mat. 44(1), 161–175 (1980) (in Russian)

    Google Scholar 

  20. Lu G., Wang P.: PDE perspective of the normalized infinity Laplacian. Commun. Partial Differ. Equ. 33(10–12), 1788–1817 (2008)

    Article  MATH  Google Scholar 

  21. Lu G., Wang P.: Inhomogeneous infinity Laplace equation. Adv. Math. 217(4), 1838–1868 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  22. Lu, G., Wang, P.: Infinity Laplace equation with non-trivial right-hand side. Electron. J. Differ. Equ. 2010(77), 1–12 (2010)

    Google Scholar 

  23. Peres Y., Schramm O., Sheffield S., Wilson D.: Tug-of-war and the infinity Laplacian. J. Am. Math. Soc. 22(1), 167–210 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  24. Peres Y., Sheffield S.: Tug-of-war with noise: a game theoretic view of the p-Laplacian. Duke Math. J. 145(1), 91–120 (2008)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Author notes

  1. Agnese Di Castro

    Present address: Dipartimento di Matematica, Università degli Studi di Parma, Parco Area delle Scienze 53/A, 43124, Parma, Italy

Authors and Affiliations

  1. Department of Mathematics, The University of Texas, 1 University Station C1200, Austin, TX, 78712, USA

    Fernando Charro & Davi Máximo

  2. Scuola Normale Superiore, p.za dei Cavalieri 7, 56126, Pisa, Italy

    Guido De Philippis

  3. CMUC, Department of Mathematics, University of Coimbra, 3001-454, Coimbra, Portugal

    Agnese Di Castro

Authors
  1. Fernando Charro
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guido De Philippis
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Agnese Di Castro
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Davi Máximo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fernando Charro.

Additional information

Communicated by O. Savin.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Charro, F., De Philippis, G., Di Castro, A. et al. On the Aleksandrov–Bakelman–Pucci estimate for the infinity Laplacian. Calc. Var. 48, 667–693 (2013). https://doi.org/10.1007/s00526-012-0567-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00526-012-0567-3

Keywords

Search

Navigation