Skip to main content
SpringerLink
Log in

A novel qualitative risk assessment using the interval-valued spherical fuzzy extension of TOPSIS method: a case study in rail transit systems

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

A Correction to this article was published on 04 January 2024

This article has been updated

Abstract

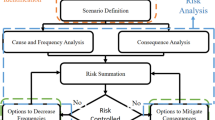
This article introduces an innovative approach for risk assessment in rail transit systems, addressing the limitations of traditional methodologies. Our proposed method combines the modified Fine–Kinney approach with the interval-valued spherical fuzzy extension of the technique for order of preference by similarity to ideal solution (IVSF-TOPSIS). By leveraging interval-valued fuzzy sets and spherical fuzzy sets, we capture nuanced uncertainties more effectively. This study differs from previous risk assessment methods by integrating IVSF sets into Fine–Kinney methodologies. Unlike traditional methods, our approach integrates IVSF sets to enhance the handling of uncertainty, resulting in a more comprehensive risk assessment. The proposed model includes parameters such as cost, preventability, and personal protective use, alongside severity, probability, and frequency. This inclusion, alongside expert opinions, enriches the analysis and ensures a more realistic risk evaluation. Applied to the Antalya rail transit (ANTRAY) system in Turkey, the study demonstrates the method’s applicability through a comprehensive case study. Four experts with extensive field and academic experience in rail transit systems and risk analysis contributed their evaluations, ensuring the thoroughness and accuracy of the results. Limited experts’ input yields consistent and high-correlation findings, enhancing result validity and applicability. Eight most exposed hazard groups, analyzed in this study, aid in producing applicable solutions for risk mitigation. The outcomes provide a prioritized list of risks and actionable insights for managing these risks effectively. By combining quantitative and qualitative data through interval-valued fuzzy sets, our approach bridges the gap between different types of information, resulting in a holistic and reliable risk assessment. Consequently, our novel methodology not only overcomes the limitations of traditional approaches but also offers a practical and comprehensive framework for decision making. By providing a clearer understanding of uncertainties and their impacts, our approach contributes to safer and more efficient rail transit operations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Change history

References

  1. Woodruff JM (2005) Consequence and likelihood in risk estimation: a matter of balance in UK health and safety risk assessment practice. Saf Sci 43:345–353

    Google Scholar 

  2. Reniers GL, Dullaert W, Ale BJM, Soudan K (2005) Developing an external domino accident prevention framework: Hazwim. J Loss Prev Process Ind 18:127–138

    Google Scholar 

  3. An M, Chen Y, Baker CJ (2011) A fuzzy reasoning and fuzzy-analytical hierarchy process based approach to the process of railway risk information: a railway risk management system. Inf Sci 181:3946–3966

    Google Scholar 

  4. An M, Lin W, Huang S (2013) An ıntelligent railway safety risk assessment support system for railway operation and maintenance analysis. Open Transp J. 7

  5. Gul M, Celik E (2018) Fuzzy rule-based Fine-Kinney risk assessment approach for rail transportation systems. Hum Ecol Risk Assess Int J 24:1786–1812

    CAS  Google Scholar 

  6. Wang Y, Li M, Zhou J, Zheng H (2022) Sudden passenger flow characteristics and congestion control based on intelligent urban rail transit network. Neural Comput Appl. 1–10

  7. Jiang Z, Song G, Qian Y, Wang Y (2022) A deep learning framework for detecting and localizing abnormal pedestrian behaviors at grade crossings. Neural Comput Appl 34(24):22099–22113

    Google Scholar 

  8. An M, Huang S, Baker CJ (2007) Railway risk assessment - the fuzzy reasoning approach and fuzzy analytic hierarchy process approaches: a case study of shunting at waterloo depot. Proceed Inst Mech Eng F J Rail Rapid Transit 221:365–383

    Google Scholar 

  9. Tixier J, Dusserre G, Salvi O, Gaston D (2002) Review of 62 risk analysis methodologies of industrial plants. J Loss Prev Process Ind 15:291–303

    Google Scholar 

  10. Marhavilas PK, Koulouriotis D, Gemeni V (2011) Risk analysis and assessment methodologies in the work sites: on a review, classification and comparative study of the scientific literature of the period 2000–2009. J Loss Prev Process Ind 24:477–523

    Google Scholar 

  11. Gul M, Guneri AF (2016) A fuzzy multi criteria risk assessment based on decision matrix technique: a case study for aluminum industry. J Loss Prev Process Ind 40:89–100

    CAS  Google Scholar 

  12. Kokangül A, Polat U, Dağsuyu C (2017) A new approximation for risk assessment using the AHP and fine kinney methodologies. Saf Sci 91:24–32

    Google Scholar 

  13. Guneri AF, Gul M, Ozgurler S (2015) A fuzzy AHP methodology for selection of risk assessment methods in occupational safety. Int J Risk Assess Manag 18:319–335

    Google Scholar 

  14. Gul M, Ak MF, Guneri AF (2017) Occupational health and safety risk assessment in hospitals: a case study using two-stage fuzzy multi-criteria approach. Hum Ecol Risk Assess Int J 23:187–202

    CAS  Google Scholar 

  15. Gul M, Celik E, Akyuz E (2017) A hybrid risk-based approach for maritime applications: the case of ballast tank maintenance. Hum Ecol Risk Assess Int J 23:1389–1403

    CAS  Google Scholar 

  16. Gul M, Celik E, Aydin N, Gumus AT, Guneri AF (2016) A state of the art literature review of VIKOR and its fuzzy extensions on applications. Appl Soft Comput 46:60–89

    Google Scholar 

  17. Guneri AF, Gul M (2013) Prioritization of risk evaluation methods for occupational safety with fuzzy multi criteria decision making. In: 26th European conference on operational research, 2013. pp. 1–4

  18. Ozdemir Y, Gul M, Celik E (2017) Assessment of occupational hazards and associated risks in fuzzy environment: a case study of a university chemical laboratory. Hum Ecol Risk Assess Int J 23:895–924

    CAS  Google Scholar 

  19. An M, Lin W, Stirling A (2006) Fuzzy-reasoning-based approach to qualitative railway risk assessment. Proceed Inst Mech Eng F J Rail Rapid Transit 220:153–167

    Google Scholar 

  20. An M, Qin Y, Jia LM, Chen Y (2016) Aggregation of group fuzzy risk information in the railway risk decision making process. Saf Sci 82:18–28

    Google Scholar 

  21. Jafarian E, Rezvani MA (2012) Application of fuzzy fault tree analysis for evaluation of railway safety risks: an evaluation of root causes for passenger train derailment. Proceed Inst Mech Eng F J Rail Rapid Transit 226:14–25

    Google Scholar 

  22. Hong L, Ouyang M, Peeta S, He X, Yan Y (2015) Vulnerability assessment and mitigation for the Chinese railway system under floods. Reliab Eng Syst Saf 137:58–68

    Google Scholar 

  23. Sarkar D (2015) Application of fuzzy failure mode effect analysis and expected value method for project risk analysis of elevated corridor metro rail projects. Int J Decis Sci Risk Manag 6:34–62

    Google Scholar 

  24. Peng Z, Lu Y, Miller A, Johnson C, Zhao T (2016) Risk assessment of railway transportation systems using timed fault trees. Qual Reliab Eng Int 32:181–194

    Google Scholar 

  25. Zhang H, Sun Q (2020) An integrated MCDM approach to train derailment risk response strategy selection. Symmetry 12:47

    ADS  CAS  Google Scholar 

  26. Demir E, Ak MF, Sarı K (2023) Pythagorean fuzzy based AHP-VIKOR integration to assess rail transportation systems in Turkey. Int J Fuzzy Syst 25(2):620–632

    Google Scholar 

  27. Gashaw T, Jilcha K (2022) Developing a fuzzy synthetic evaluation model for risk assessment: a case of Addis-Djibouti railway construction project. Innovat Infrastruct Solutions 7(2):154

    Google Scholar 

  28. Huang Y, Zhang Z, Tao Y, Hu H (2022) Quantitative risk assessment of railway intrusions with text mining and fuzzy rule-based bow-tie model. Adv Eng Inform 54:101726

    Google Scholar 

  29. Park J, Park C, Ahn S (2018) Assessment of structural risks using the fuzzy weighted Euclidean FMEA and block diagram analysis. Int J Adv Manuf Technol. 99

  30. Park CW, Wang JB, Kwak SL, Choi DB (2010) Modeling and assessing of train-person collision accidents on the national railway of South Korea. Environment 2:1

    Google Scholar 

  31. Azadeh A, Salehi V, Kianpour M (2018) Performance evaluation of rail transportation systems by considering resilience engineering factors: Tehran railway electrification system. Transp Lett 10:12–25

    Google Scholar 

  32. Deng H (1999) Multicriteria analysis with fuzzy pairwise comparison. Int J Approximate Reason 21:215–231

    Google Scholar 

  33. Kinney GF, Wiruth AD (1976) Practical risk analysis for safety management. Naval Weapons Center, China Lake, CA

  34. Wang W, Liu X, Qin Y (2018) A fuzzy Fine-Kinney-based risk evaluation approach with extended MULTIMOORA method based on choquet integral. Comput Ind Eng 125:111–123

    ADS  CAS  Google Scholar 

  35. Gul M, Ak MF (2021) A modified failure modes and effects analysis using interval-valued spherical fuzzy extension of TOPSIS method: case study in a marble manufacturing facility. Soft Comput 25:6157–6178

    Google Scholar 

  36. Sleeper LA, Reynolds HR, White HD, Webb JG, Džavík V, Hochman JS (2010) A severity scoring system for risk assessment of patients with cardiogenic shock: a report from the SHOCK trial and registry. Am Heart J 160:443–450

    PubMed  PubMed Central  Google Scholar 

  37. Azadeh-Fard N, Schuh A, Rashedi E, Camelio JA (2015) Risk assessment of occupational injuries using accident severity grade. Saf Sci 76:160–167

    Google Scholar 

  38. Leite M, Infante V, Andrade AR (2022) Using expert judgement techniques to assess reliability for long service-life components: an application to railway wheelsets. Proceed Inst Mech Eng O J Risk Reliabil 236(5):879–892

    Google Scholar 

  39. Wang LZ, Pei YL, Liu BT (2012) Risk factors for the injury severity of fatigue-related traffic accidents. Adv Eng Forum 5:61–65

    Google Scholar 

  40. Moore-Ede M, Heitmann A, Guttkuhn R, Trutschel U, Aguirre A, Croke D (2004) Circadian alertness simulator for fatigue assessment in transportation: application to reduce frequency and severity of truck accidents. Aviat Space Environ Med 75:A107–A118

    PubMed  Google Scholar 

  41. Dubois AE, Turner PJ, Hourihane J et al (2018) How does dose impact on the severity of food-induced allergic reactions, and can this improve risk assessment for allergenic foods? Allergy 73:1383–1392

    CAS  PubMed  Google Scholar 

  42. Liu HC (2016) FMEA using uncertainty theories and MCDM methods. In: FMEA using uncertainty theories and MCDM methods. Springer, Singapore, pp. 13–27

  43. Liu HC, Chen XQ, Duan CY, Wang YM (2019) Failure mode and effect analysis using multi-criteria decision making methods: a systematic literature review. Comput Ind Eng 135:881–897

    Google Scholar 

  44. Deng W, Li N, Zheng H, Lin H (2016) Occurrence and risk assessment of antibiotics in river water in Hong Kong. Ecotoxicol Environ Saf 125:121–127

    CAS  PubMed  Google Scholar 

  45. Pinto A, Nunes IL, Ribeiro RA (2011) Occupational risk assessment in construction industry—overview and reflection. Saf Sci 49:616–624

    Google Scholar 

  46. Gul M, Yucesan M, Celik E (2020) A manufacturing failure mode and effect analysis based on fuzzy and probabilistic risk analysis. Appl Soft Comput 96:106689

    Google Scholar 

  47. Aminbakhsh S, Gunduz M, Sonmez R (2013) Safety risk assessment using analytic hierarchy process (AHP) during planning and budgeting of construction projects. J Saf Res 46:99–105

    Google Scholar 

  48. Bahr NJ (2014) System safety engineering and risk assessment: a practical approach, 2nd edn. CRC Press, Boca Raton

    Google Scholar 

  49. Stoessel F (2021) Thermal safety of chemical processes: risk assessment and process design, 2nd edn. Wiley-VCH, Weinheim

    Google Scholar 

  50. Albert A, Hallowell MR (2013) Safety risk management for electrical transmission and distribution line construction. Saf Sci 51:118–126

    Google Scholar 

  51. Di Bona G, Silvestri A, Forcina A, Petrillo A (2018) Total efficient risk priority number (TERPN): a new method for risk assessment. J Risk Res 21:1384–1408

    Google Scholar 

  52. Von Ahsen A (2008) Cost-oriented failure mode and effects analysis. Int J Qual Reliabil Manag 25:466–476

    Google Scholar 

  53. Rezaee MJ, Salimi A, Yousefi S (2017) Identifying and managing failures in stone processing industry using cost-based FMEA. Int J Adv Manuf Technol 88:3329–3342

    Google Scholar 

  54. Chen JK (2017) Prioritization of corrective actions from utility viewpoint in FMEA application. Qual Reliab Eng Int 33:883–894

    Google Scholar 

  55. Deng H, Yeh CH, Willis RJ (2000) Inter-company comparison using modified TOPSIS with objective weights. Comput Oper Res 27:963–973

    Google Scholar 

  56. Demir E (2018) Approach for siting a support facility for transporting supplies in emergency cases in the republic of Bulgaria. In: MATEC Web of Conferences, EDP Sciences. 234:06001

  57. Demir E (2022) Weiszfeld, tree-seed, and whale optimization algorithms comparison via locating transportation facilities with weightings considering the vulnerability and uncertainty. PLoS ONE 17(6):e0269808

    CAS  PubMed  PubMed Central  Google Scholar 

  58. Demir E (2020) Network distance coefficient effect on determining transportation facility location. In: HI Kurt (ed) Academic studies in engineering sciences, Livre de Lyon, Lyon, France, 2020, pp. 171–181.

  59. Yucesan M, Gul M, Celik E (2021) A holistic FMEA approach by fuzzy-based Bayesian network and best-worst method. Complex Intell Syst 7:1547–1564

    Google Scholar 

  60. Kutlu Gündoğdu F, Kahraman C (2019) A novel fuzzy TOPSIS method using emerging interval-valued spherical fuzzy sets. Eng Appl Artif Intell 85:307–323

    Google Scholar 

  61. Yucesan M, Gul M (2020) Hospital service quality evaluation: an integrated model based on pythagorean fuzzy AHP and fuzzy TOPSIS. Soft Comput 24:3237–3255

    Google Scholar 

  62. Dogan B, Oturakci M, Dagsuyu C (2022) Action selection in risk assessment with fuzzy Fine–Kinney-based AHP-TOPSIS approach: a case study in gas plant. Environ Sci Pollut Res 29:66222–66234. https://doi.org/10.1007/s11356-022-20498-2

    Article  CAS  Google Scholar 

  63. Oturakçı M, Dağsuyu C (2017) Fuzzy Fine-Kinney approach in risk assessment and an application Karaelmas. J Occupat Health Saf. https://doi.org/10.33720/kisgd.327548

Download references

Acknowledgements

Thanks are due to everyone for assisting in completing the data collection.

Funding

No funding was received for conducting this study.

Author information

Authors and Affiliations

  1. Department of Industrial Engineering, Antalya Bilim University, 07190, Antalya, Turkey

    Muhammet Fatih Ak

  2. Department of Civil Engineering, Antalya Bilim University, 07190, Antalya, Turkey

    Emre Demir

Authors
  1. Muhammet Fatih Ak
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Emre Demir
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

MFA and ED contributed to the research design and implementation, the results analysis, and the manuscript’s writing.

Corresponding author

Correspondence to Muhammet Fatih Ak.

Ethics declarations

Conflict of interest

No potential conflict of interest was reported by the authors.

Ethical approval

This article does not contain any studies with animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The original online version of this article was revised to correct the affiliation of Author Emre Demir.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ak, M.F., Demir, E. A novel qualitative risk assessment using the interval-valued spherical fuzzy extension of TOPSIS method: a case study in rail transit systems. Neural Comput & Applic 36, 5109–5132 (2024). https://doi.org/10.1007/s00521-023-09224-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-023-09224-2

Keywords

Search

Navigation